1. Norms
Norm
- length of vectors

Manhattan Norm

Euclidean Norm

이 책에서는 언급이 없으면 Euclidean norm을 사용할 것이다.
2. Inner Products
Inner products의 major purpose는 vectors가 서로 orthogonal한지를 결정하는 것임.
2.1 Dot Product
이것은 우리가 흔히 익숙한 scalar product/dot product이다. 우리는 앞으로 이 특정 inner product를 dot product라고 부를 것임.
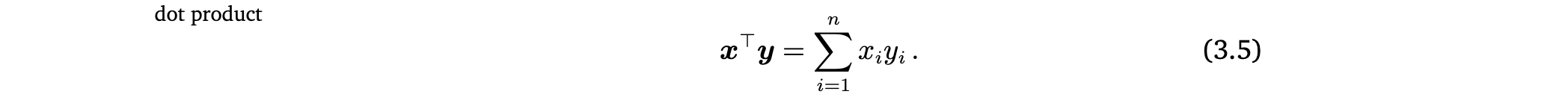
하지만 inner product는 특정 성질을 가지고 있는 더 일반적인 concept이다.
2.2 General Inner Products
Bilinear mapping Ω
- 두 arguments로 된 mappping
- 각 argument에서 linear
- vector space V에서 x,y,z ∈ V, λ,ψ ∈ 일때 다음을 만족함.
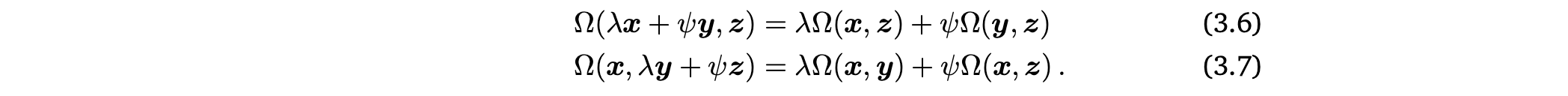
Symmetric, positive definite
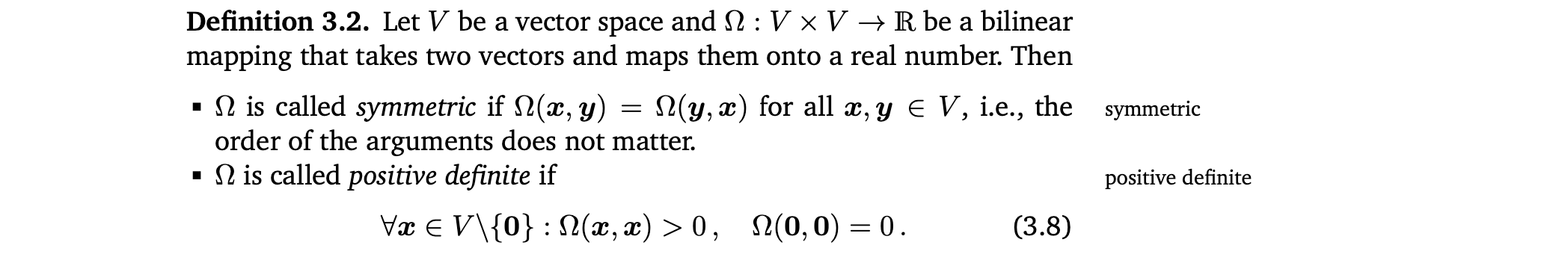
Inner product, Inner product space
- positive definite, symmetric bilinear mapping Ω : V x V -> 를 V에 inner product하고 부르고 Ω(x,y) 대신에 <x,y>라고 쓴다.
- pair (V, <·,·>)를 inner product space 또는 (real) vector space with inner product라고 부름.
- dot product를 사용하는 경우 (V, <·,·>)를 Euclidean vector space라고 부름.
- 이 책에서는 inner product space라고 할 것.


2.3 Symmetric, Positive Definite Matrices

👉 Example 3.4 (Symmetric, Positive Definite Matrix)
Inner product와 symmetric,positive definite matrix의 관계

3. Lengths and Distances
inner product가 norm을 유도할 수 있다는 점에서 inner product와 norm은 밀접하게 관련되어 있음.
하지만 Manhattan norm과 같이 inner product에 의해 유도되지 않은 norm도 있음.
여기서는 inner products에 의해 유도되는 norm에 집중할 것임.

👉 Example 3.5 (Lengths of Vectors Using Inner Products)
Cauchy-Schwarz Inequality

Distance and Metric
Distance
Euclidean distance
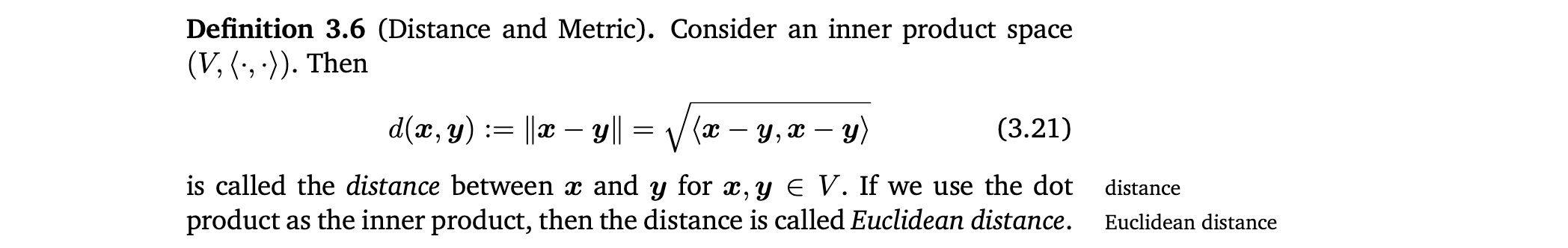
Metric
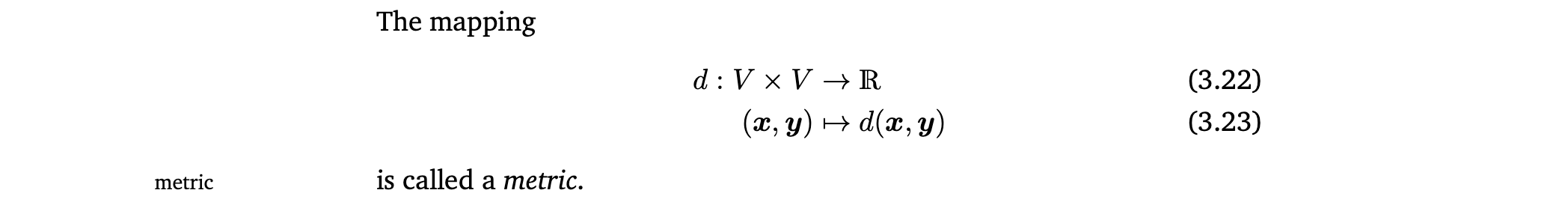
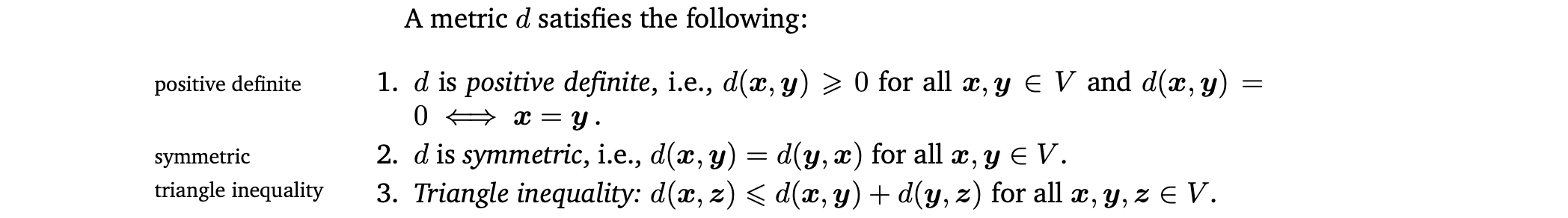
4. Angles and Orthogonality
inner product spaces에서 두 vector간의 angle을 정의하기 위해 Cauchy-Schwarz inequality를 사용한다.
Angle

👉 Example 3.6 (Angle between Vectors)
Orthogonality
Orthogonality
Orthonormal

👉 Example 3.7 (Orthogonal Vectors)
한 inner product에 대해서 orthogonal한 두 vector가 다른 inner product에 대해서도 orthogonal 할 필요 없다.
Orthogonal Matrix
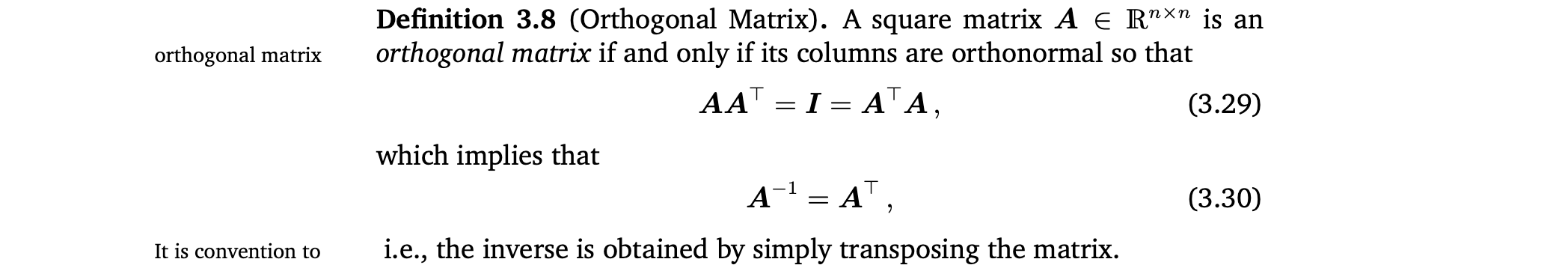
더 정확하게 말하면 orthonormal임.
즉, Orthogonal matrix의 inverse는 transpose와 같다.
Transformations by orthogonal matrices
- 두 vector를 orthogonal matrices에 의해 transformation하면 distance와 angle이 보존된다.
- orthogonal matrices는 rotation인 transformation을 정의한다.
5. Orthonormal Basis
여기서는 각 basis vector의 길이가 1이고, basis vectors가 서로 orthogonal한 특별한 경우를 다룸. 이러한 basis를 orthonormal basis라고 부름.
Orthonormal Basis(ONB)
Orthonormal Basis(ONB)
Orthogonal Basis

- Inner product가 dot product일 때, Euclidean vector space에서의 canonical/standard basis는 orthonormal basis
- 두 basis가 orthonormal basis인지 보기 👉 Example 3.8 (Orthonormal Basis)
Gram-Schmidt process
A set of non-orthogonal and unnormalized basis vectors가 주어졌을 때, 각 basis vector를 column으로 하는 matrix를 만들고 다음과 같은 augmented matrix에 Gaussian elimination을 적용하여 orthonormal basis를 얻는 방법

6. Orthogonal Complement
이제 서로 orthogonal한 vector space에 대해 알아봄.
Orthogonal Complement
- D차원 vector space V와 M차원 subspace U ⊆ V 가 있을 때, orthogonal complement 는 V의 (D-M)차원 subspace임
- V에 있는 모든 vector는 U에 있는 모든 vector에 orthogonal함
- ∩ = {0} 이므로 모든 vector x ∈ V는 다음과 같이 uniquely decomposed될 수 있다.
- (,...,)은 U의 basis, (,...,)은 의 basis
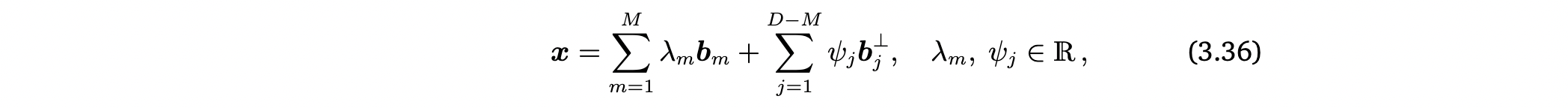
- (,...,)은 U의 basis, (,...,)은 의 basis
normal vector
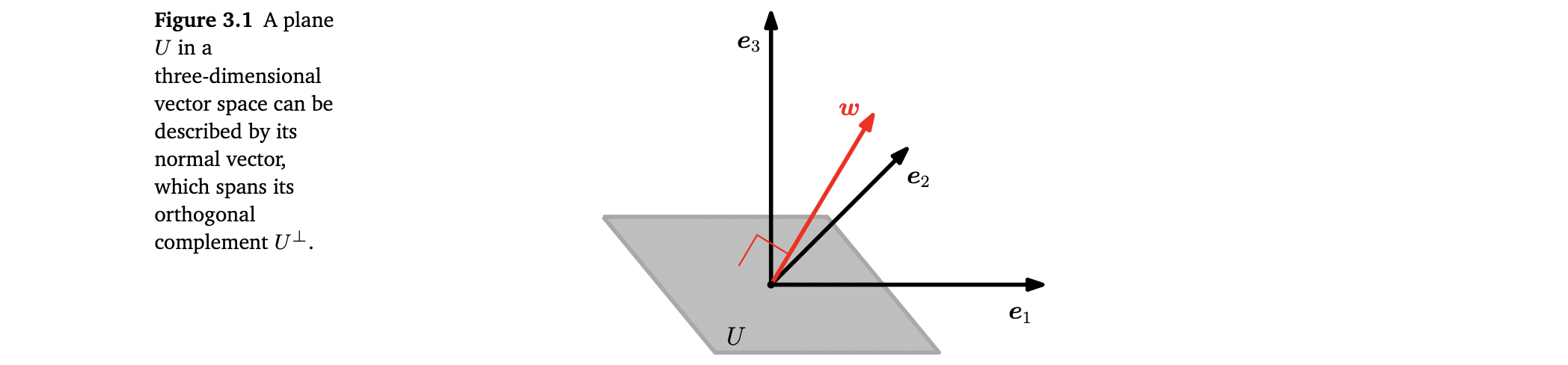
- plane U에 orthogonal한 ∥w∥ =1 인 vector w는 의 basis vector
- w에 orthogonal한 모든 vectors는 plane U에 놓여있어야 함. 이 때의 w를 U의 normal vector라고 함.
일반적으로 orthogonal complements는 n-dimensional vector에서의 hyperplanes와 affine spaces를 설명하는 데 사용된다.
7. Inner Product of Functions
두 function u : R -> R과 v : R-> R 의 inner product는 다음과 같은 definite integral로 정의할 수 있음.
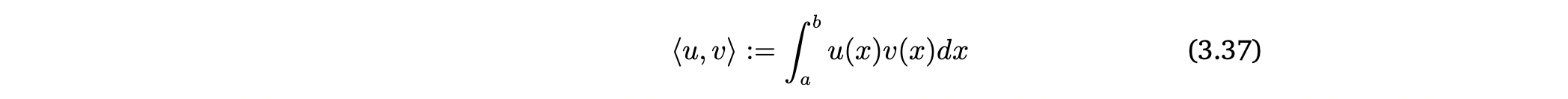
- vector일때와 똑같이 norm과 orthogonality를 정의할 수 있음.
- 계산 값이 0이면 두 function은 orthogonal
👉 Example 3.9 (Inner Product of Functions)
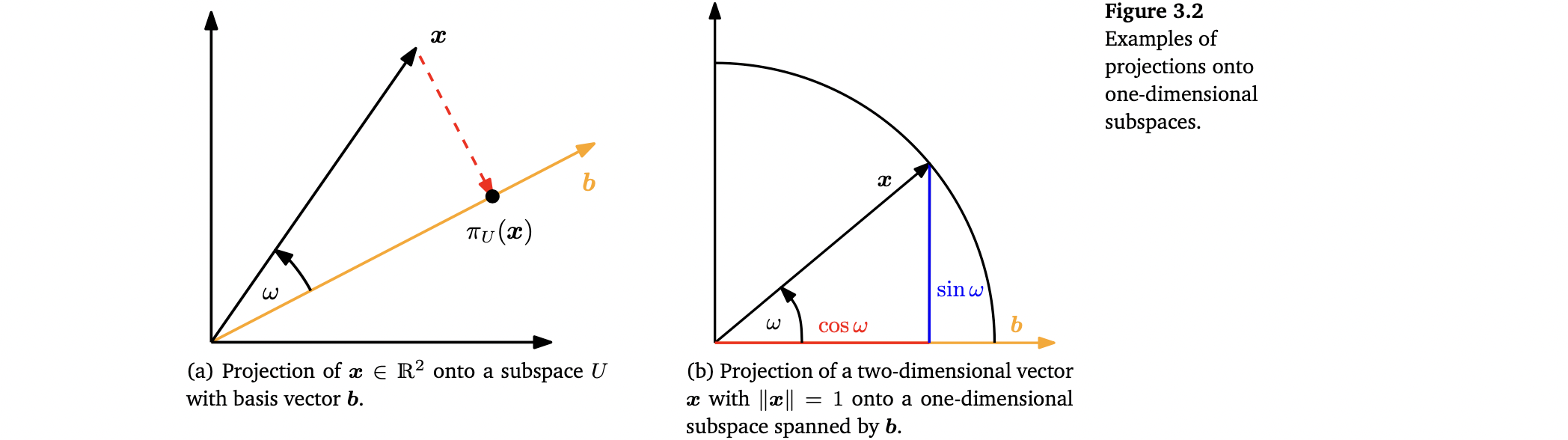
8. Orthogonal Projections
Projection
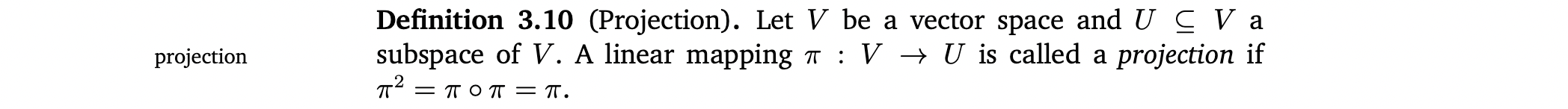
Projection matrix
Linear mapping은 transformation matrix로 표현될 수 있음.
= 성질을 만족하는 특별한 종류의 transformation matrix 를 projection matrix라고 부름.
앞으로 특별한 언급 없으면 dot product를 inner product라고 가정함.
8.1 Projection onto One-Dimensional Subspaces (Lines)
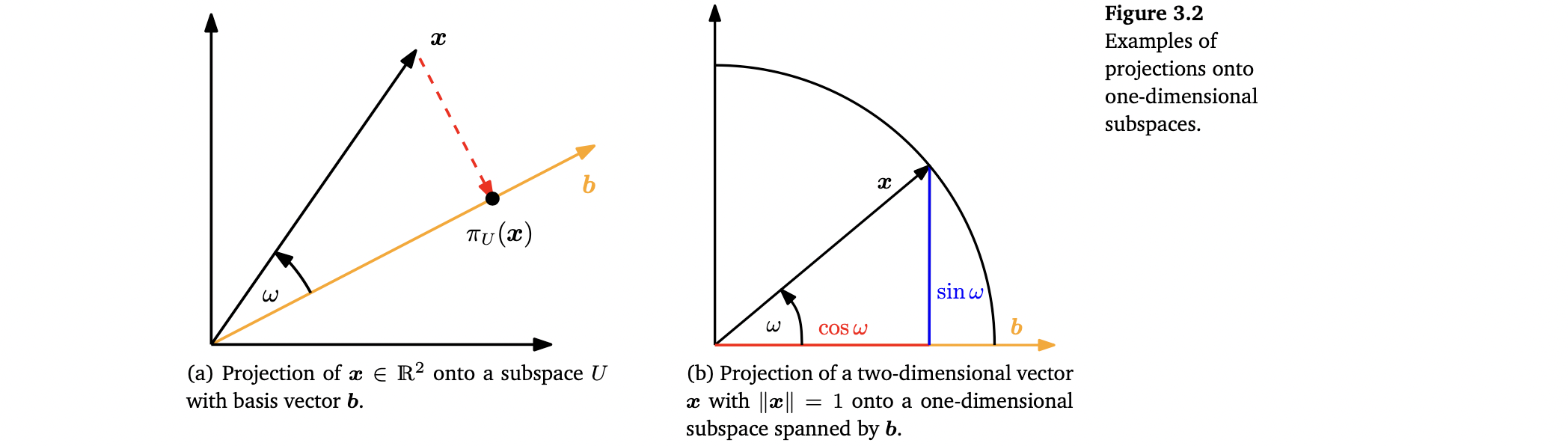

3-step procedure to determine coordinate λ, projection ∈ U, projection matrix
- coordinate λ of the projection

-
projection point ∈ U

-
Finding the projection matrix

- projection matrix는 항상 symmetric함.
- projection 은 여전히 n-dimensional vector이다. 하지만 우리는 더이상 이 projection을 표현하기 위해 n coordinates가 필요하지 않고, subspace U를 span하는 basis vector b에 대해 표현을 하고 싶으면 1차원의 λ만 필요하다.
👉 Example 3.10 (Projection onto a Line)
8.2 Projection onto General Subspaces
3-step procedure to find the projection and the projection matrix
-
coordinates , ... , of the projection (with respect to the basis of U)
normal equation
pseudo-inverse of B
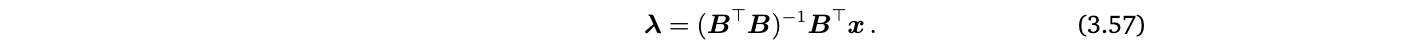
-
projection ∈ U
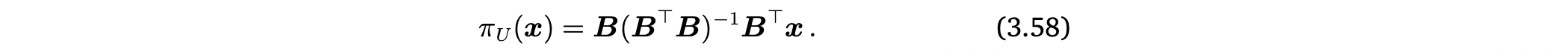
- projection matrix
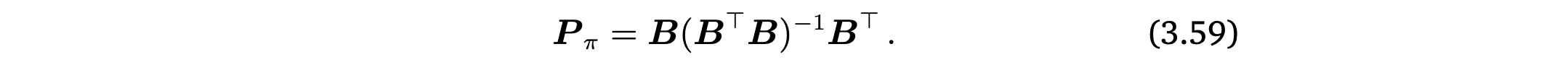
👉 Example 3.11 (Projection onto a Two-dimensional Subspace)
- projections 은 여전히 n-dimensional vector이다. 하지만 우리는 더이상 이 projected vector을 표현하기 위해 n coordinates가 필요하지 않고, subspace U의 basis vectors , ... , 에 대한 m coordinates , ... , 만 필요함.
Projections는 linear system Ax=b가 solution이 없을 때 approximate solution을 구할 수 있음.
A의 column들로부터 span되는 subspace에 대한 b의 orthogonal projection을 계산함으로써 가장 가까운 b를 구할 수 있음. 이로써 구한 solution을 least-squares solution이라고 함.
basis가 ONB인 경우
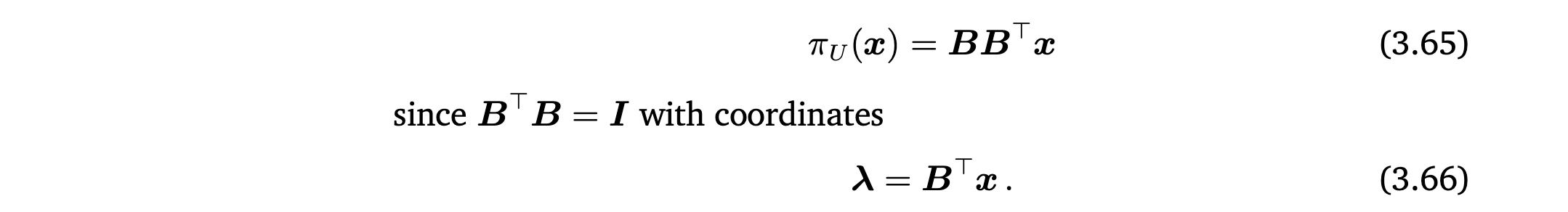
8.3 Gram-Schmidt Orthogonalization
n-dimensional vector space V의 아무 basis (, ... , )을 V의 orthogonal/orthonormal basis (, ... , )로 transform해준다. 이러한 basis는 항상 존재.
방식은 다음과 같음.
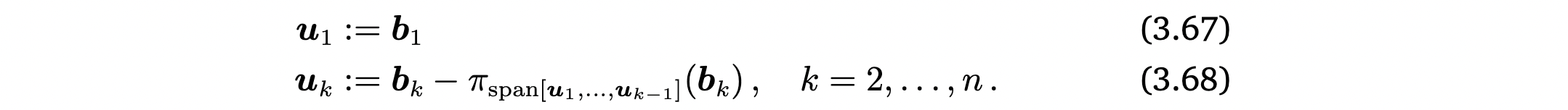
그리고 구한 를 normalize해주면 ONB를 얻을 수 있음.
👉 Example 3.12 (Gram-Schmidt Orthogonalization)
8.4 Projection onto Affine Subspaces
지금까지는 vector를 lower-dimensional subspace U에 어떻게 projection하는지를 배움. 지금은 vector를 affine subspace에 projection하는 방법을 배움
affine space L = + U 가 주어졌을 때 x를 L로의 orthogonal projection (x)을 결정하는 문제를 풀기위해 vector subspace로의 projection으로 문제를 바꾼다.
-> vector subspace L - = U를 define, projection ( - )을 얻음
orthogonal projection onto an affine space L은 구한 ( - )에서 를 더함으로써 얻을 수 있음
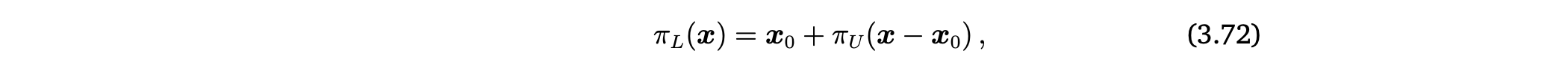
- 는 L의 direction space
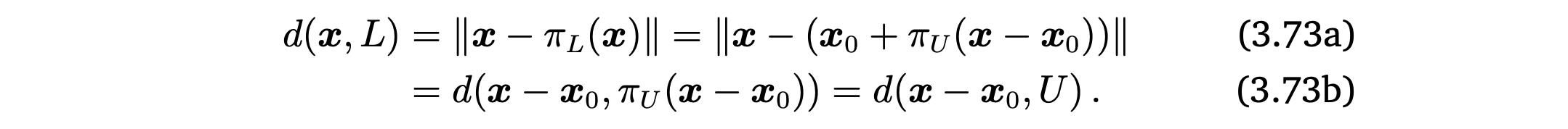
- affine space L로부터 x의 거리는 U로부터 - 의 거리와 같다
9. Rotations
Rotation
- plane을 origin에 대해 angle θ만큼 rotate한 linear mapping (automorphism of a Euclidean vector space)
9.1 Rotations in
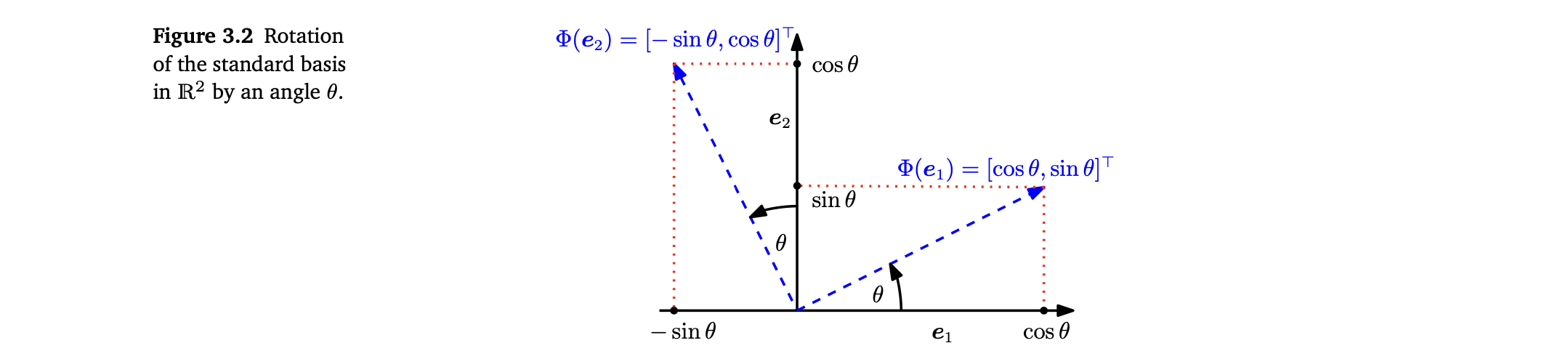
-
rotated vectors는 여전히 linearly independent, 즉, 의 basis임. 이것은 rotation이 basis change를 수행함을 의미함.
-
Rotation Φ는 linear mapping이므로, rotation matrix R(θ)로 표현할 수 있음
Rotation matrix
rotated coordinates R(θ)로 basis change를 수행하는 rotation matrix
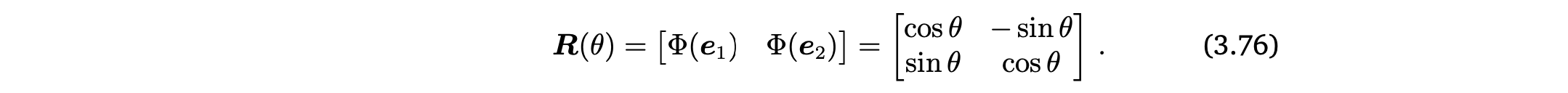
9.2 Rotations in
-
에서의 general rotation matrix를 구하는 방법 : images R, R, R를 구하고 이것들이 서로 orthonormal하도록 함
-
Rotation about the -axis
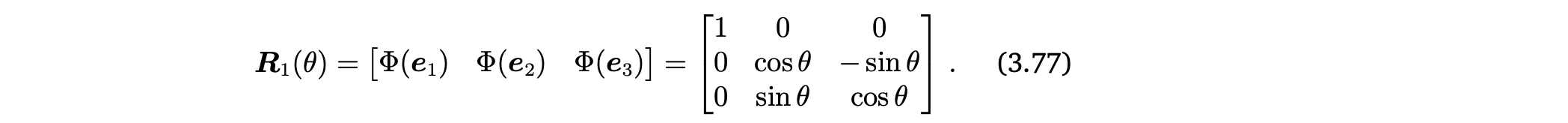
-
Rotation about the -axis
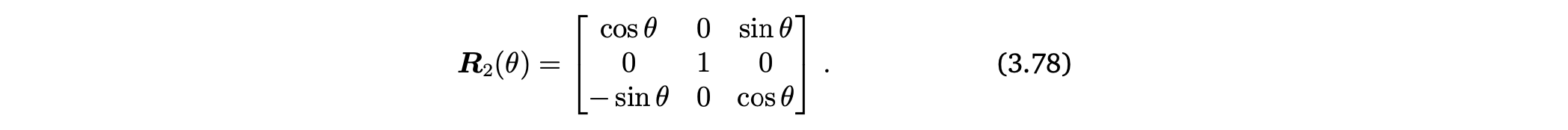
-
Rotation about the -axis
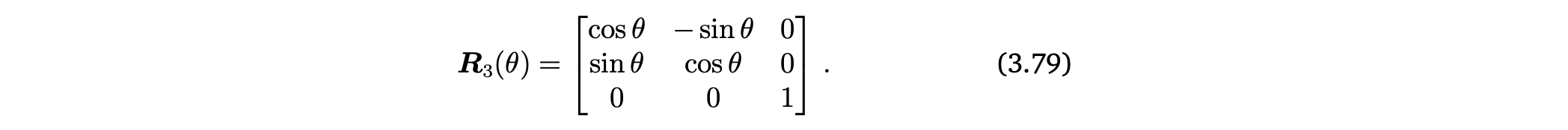
9.3 Rotations in n Dimensions
Givens Rotation
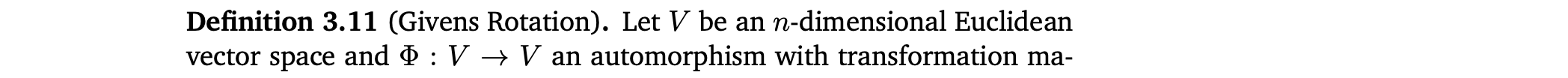
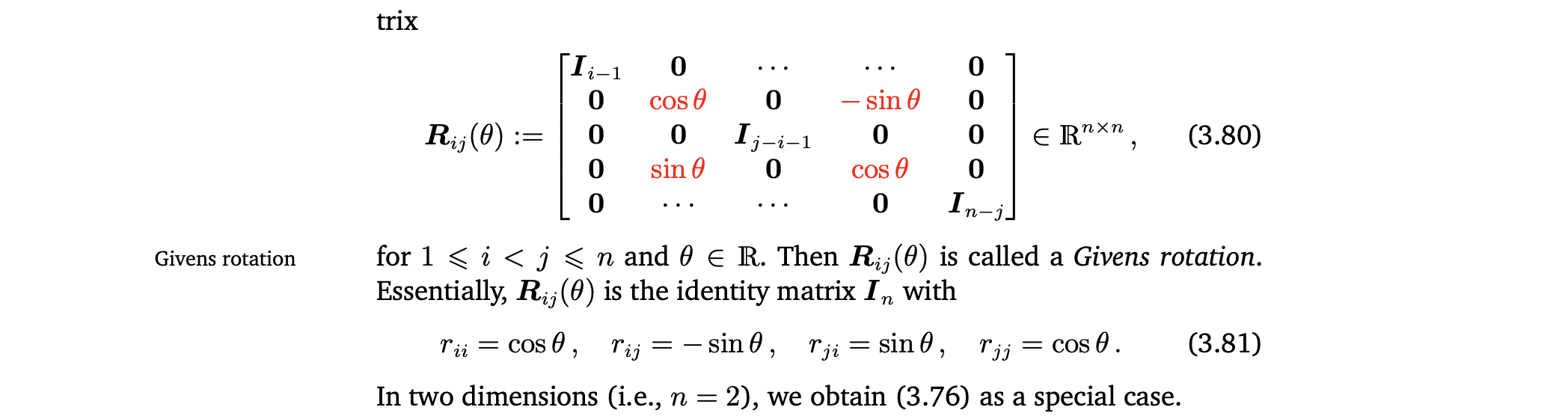
9.4 Properties of Rotations
- rotation은 distance를 보존
- rotation은 angle을 보존
- 3차원 이상에서의 rotation은 일반적으로 commutative하지 않음
- 2차원 vector에서만 rotation이 commutative. 그래서 같은 point에 대해 rotate하는 경우에만 rotation은 multiplication에 대해 Abelian group을 형성
