[AI504] Class 03: Neural Networks & Backpropagation

이채연·2023년 3월 4일

AI504

목록 보기

5/28

Logistic Regression

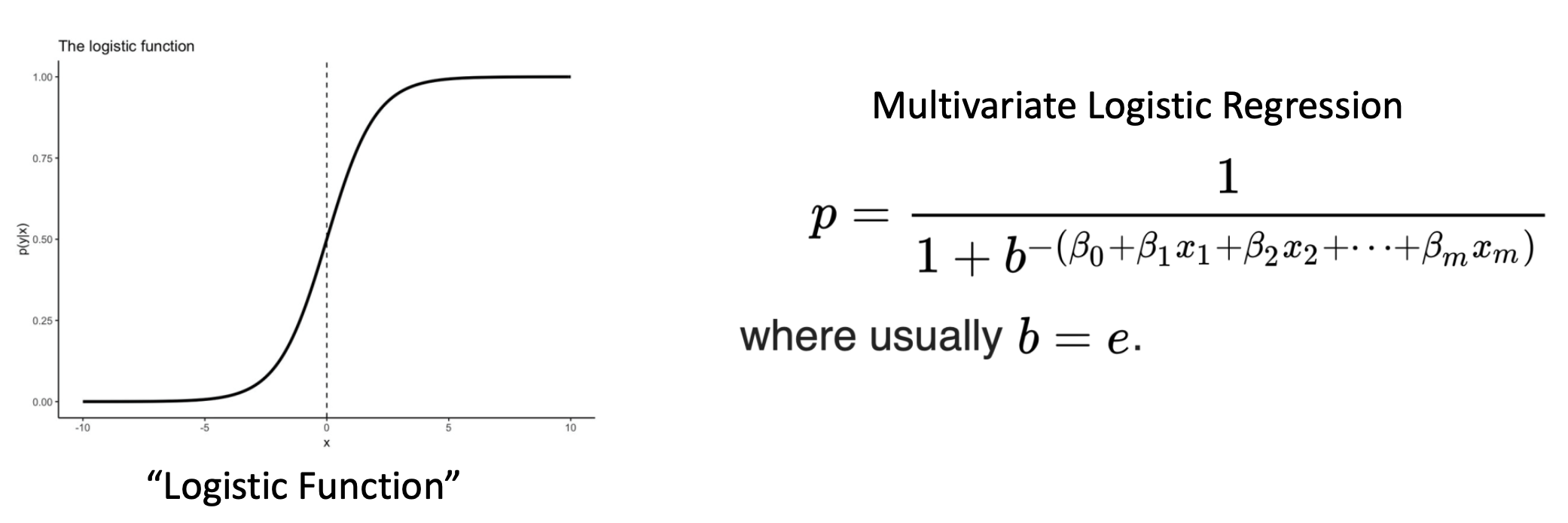
Logistic regression model은 binary outcome을 model하기에 perfect model이다. 왜냐하면 output p가 항상 0~1 사이이기 때문이다.

🔗 Odds

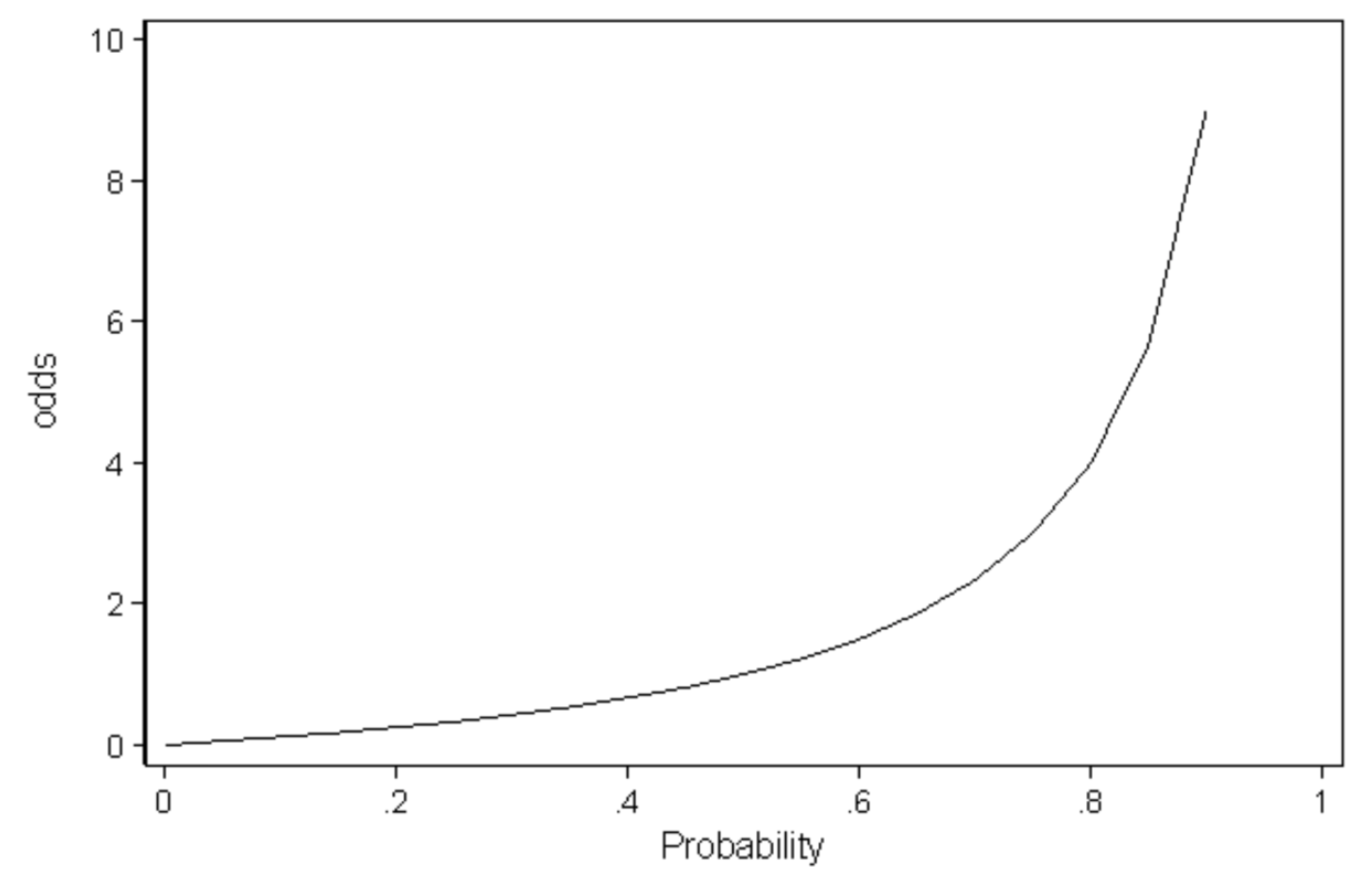
odds(p) = p/(1-p)
- p : binary situation에서 승리 확률
odds : ratio between winning and losing
이길 확률 p가 높으면 odds가 높아진다.
Ex. odds = 4 ➡️ 이길 확률이 질 확률보다 4배 많다.
장점 : probability는 [0,1]로 범위가 제한되어있는데 odds는 범위가 [0,inf)이다. range가 좀 더 자유롭다.

✔️ output의 범위를 늘리고 싶은 이유

Output의 범위가 0~1 사이이면 parameter를 carefully tuned(choice)해야한다. 하지만 범위가 [0,inf)으로 넓어지면 parameter를 tune하기 더 쉬워진다.
더 이상적인 상황은 log를 취하여, function의 output이 (-inf, inf) 범위를 가져 더 자유롭게 한다.

🔗 Log-Odds (Logit)

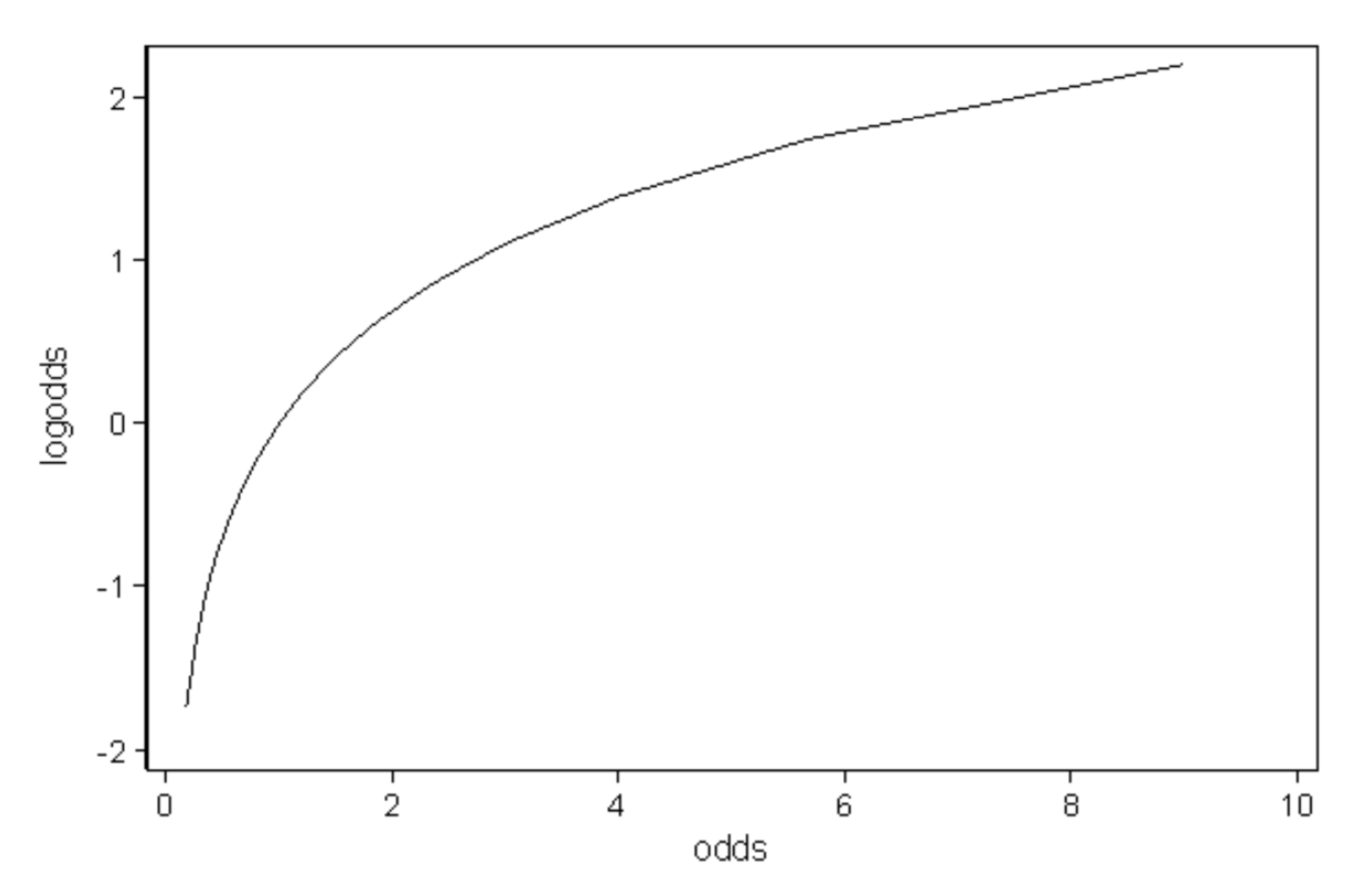
logit(p) = log(p/(1-p))
odds를 0에서 inf로 움직일 때, log-odds는 -inf에서 inf로 움직인다. (-inf,inf)
logit value는 polynomial function으로 쉽게 approximate 할 수 있다.

🔗 Linear Modeling of Logit

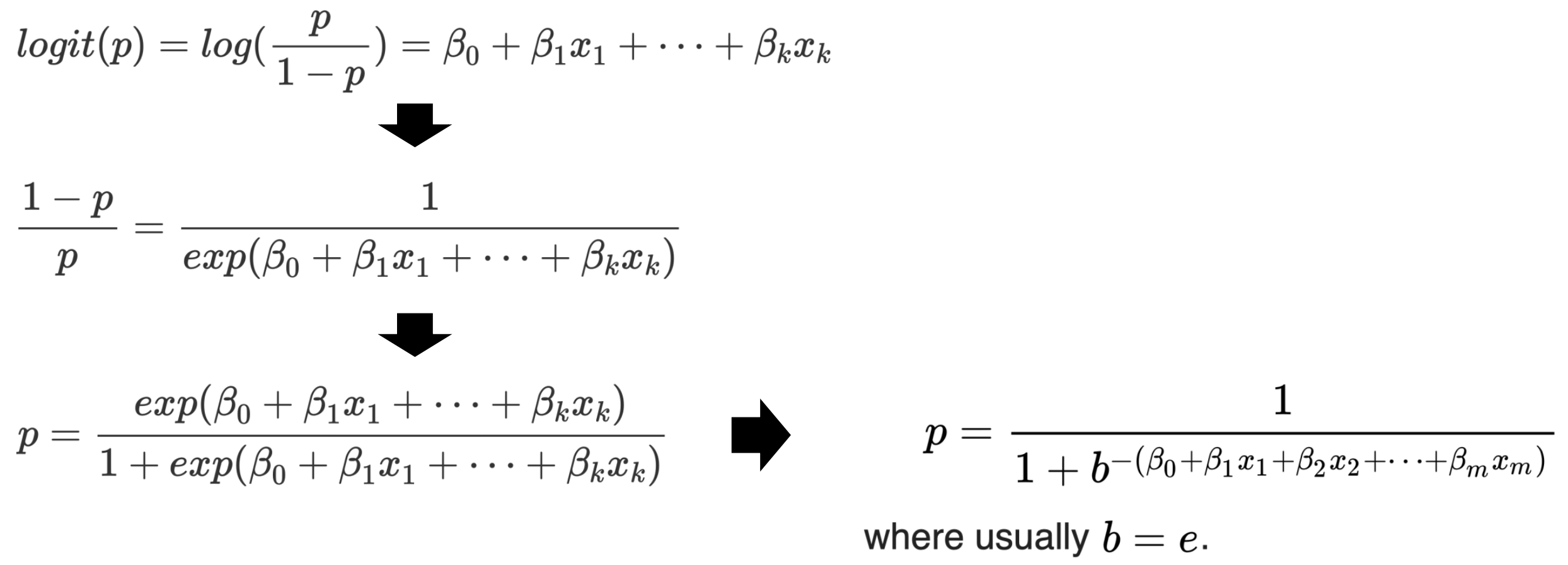
1. binary outcome variable p (event가 일어날 확률)
2. 좀 더 쉽게 하기 위해 probability->odds->log-odds(logit)
3. logit value를 linearly하게 approximate
4. 식 정리하면 logistic regression form을 얻는다.

🔗 Vector form

Inner product
p (probability of winning) 대신 $h_Θ(X)$ 라고 부른다.
이 함수의 outcome은 input X가 주어졌을 때, parameter Θ에 의해 parameterized된다.

✔️ Image classification(Binary prediction) using logistic regression

X차원이 128*128=16k 이므로 Θ도 16k차원 벡터이다.
Input X는 Image Representation Vector이다.

이제 Θ를 optimize해보자.

Maximum Likelihood Estimate (MLE)

MLE 원리를 사용하여 Θ를 optimize하여 maximize likelihood of estimate 하자. woman이면 outcome Y=1, man이면 outcome Y=0 이 나오도록 하자.

① Probability Function

logistic regression function의 goal, 원하는 Θ의 behave : $x_i$ 를 넣으면 output ŷ = $h_Θ(X)$ 이 $y_i$ 와 최대한 같길 바란다.

② Likelihood Function

sample이 서로 independent(I.I.D)하다고 가정했기 때문에 이들의 joint probability는 각 확률을 곱한 것과 같다.
Y는 bernoulli distribution을 따르는 binary variable이다.

③ Log Likelihood Function

Log를 쓰는 이유 : summation으로 만들어 multiplication으로 인한 underflow를 방지하여 다루기 쉽게 한다.
Sample의 개수로 normalize한다.

④ Negative Log Likelihood Function

loss/cost function을 최소화하고 싶기 때문에 앞에 -를 붙인다.
Negative Log Likelihood를 loss함수로 사용한다.
Negative Log Likelihood(NLL) = Cross Entropy loss
- Bernoulli Distribution에서 log를 붙이고 -를 하면 Cross Entropy loss이다.
이 NLL 함수를 gradient descent를 통해 minimize한다.

Neural Networks

뉴런으로 구성된 모델

Artificial neuron

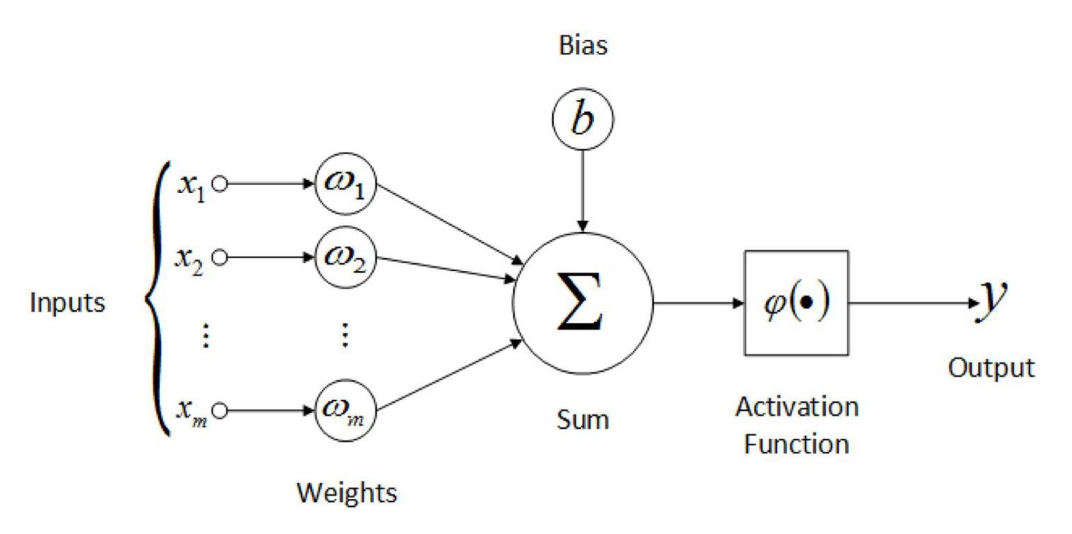
실제 neuron과 매우 유사하다.
input들로부터 signal이 온다.
하나의 single neuron을 다룰때는 주로 activation function으로 sigmoid function을 사용한다.
sigmoid function은 역치를 표현하는 함수로 보인다.

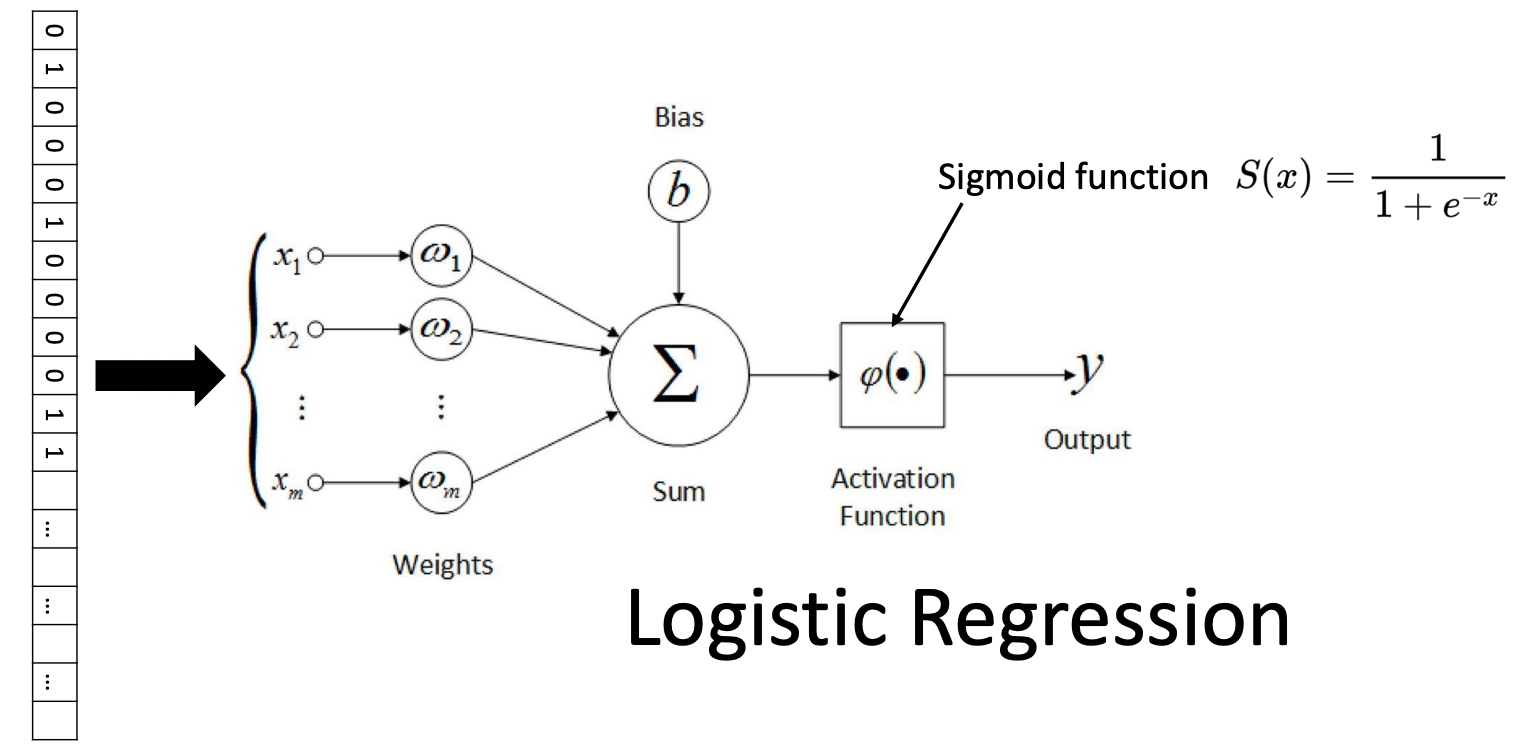
⭐️ 이 single neuron의 정체는 logistic regression이다!

Logistic regression은 activation function으로 sigmoid function을 가지는 single artificial neuron이다.
neuron(hidden neuron)의 수를 증가시키면 어떻게 logistic regression이 multi-layer perceptron으로 발전하는지 알 수 있다.

이제 또다른 neurons(hidden layer)를 추가해보자.

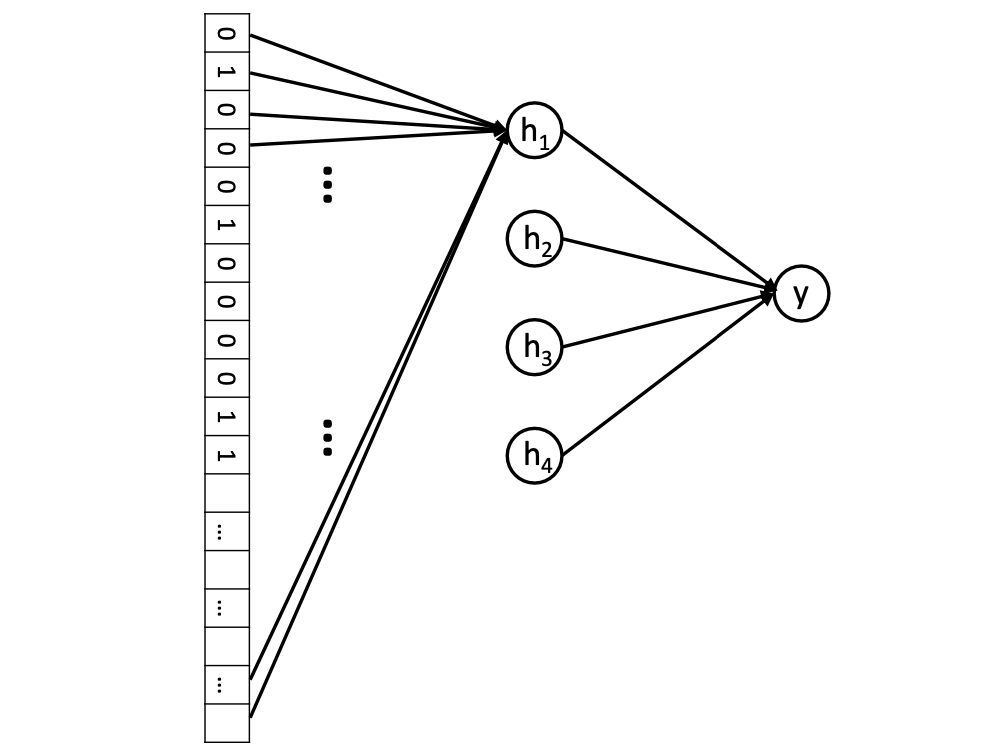
Feedforward neural network with one hidden layer of 4 neurons.
Hidden layer의 activation function은 sigmoid function이다.

4개의 neuron 각각은 모든 input 정보를 서로 다른 weight set과 함께 수집한다.
learnable weight parameter의 개수 : 4*16k = 64k

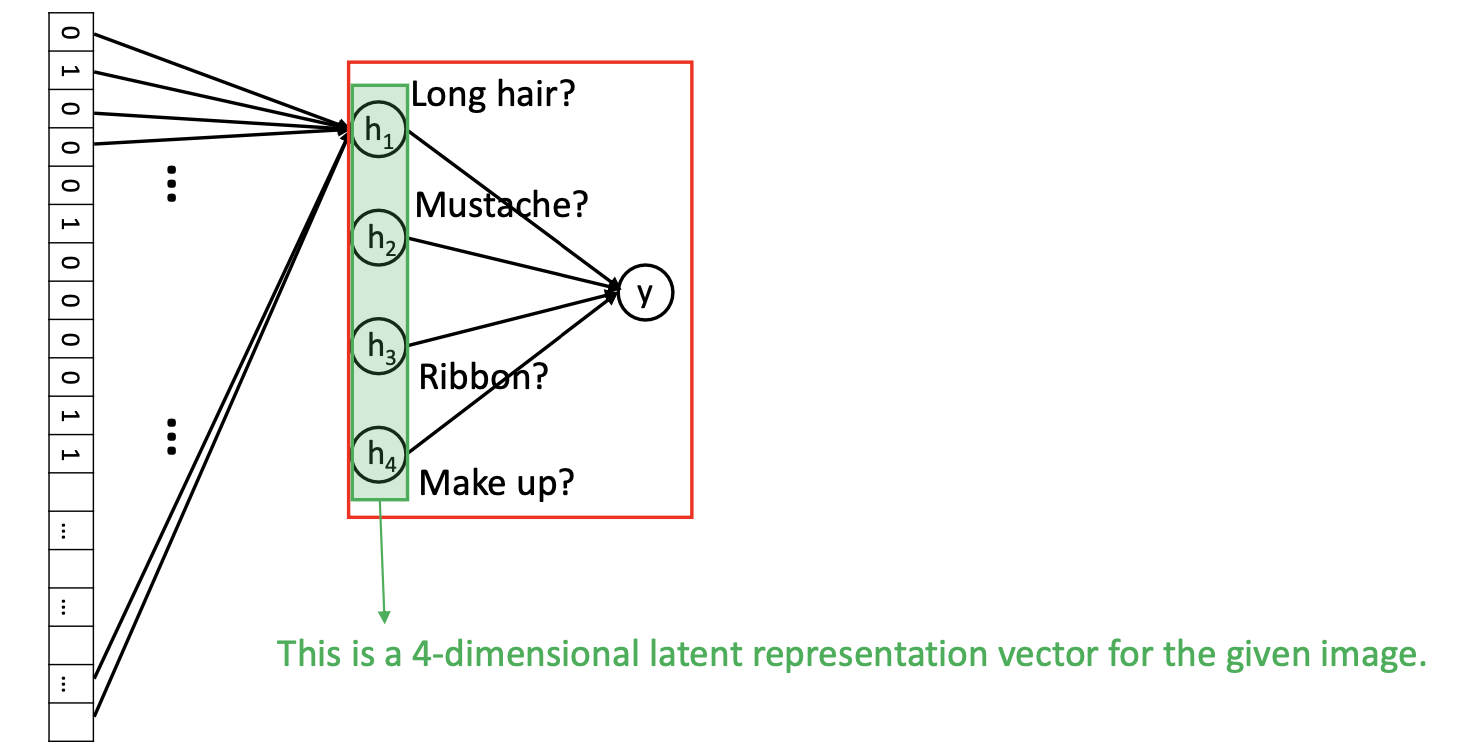
4 logistic regression classifiers (hidden layer)
- sigmoid activation을 사용하므로, 각 hidden neuron을 logistic regression으로 생각할 수 있다.
- Backpropagation을 기반으로, hidden logistic regression은 useful한 것을 학습할 것이다.
Higher-level logistic regression classifiers
- Final Logistic Regression Model은 4 dimensional input을 사용한다. Row pixel을 가지고 결정을 내리는 것이 아니라 high-level concept을 기반으로 결정을 내린다.
- 4-dimensional latent representation vector
  - model이 최종 판단을 내리는 데 도움을 줄 수 있는 semantics of image를 hidden, capsuling한다.
parameter 개수

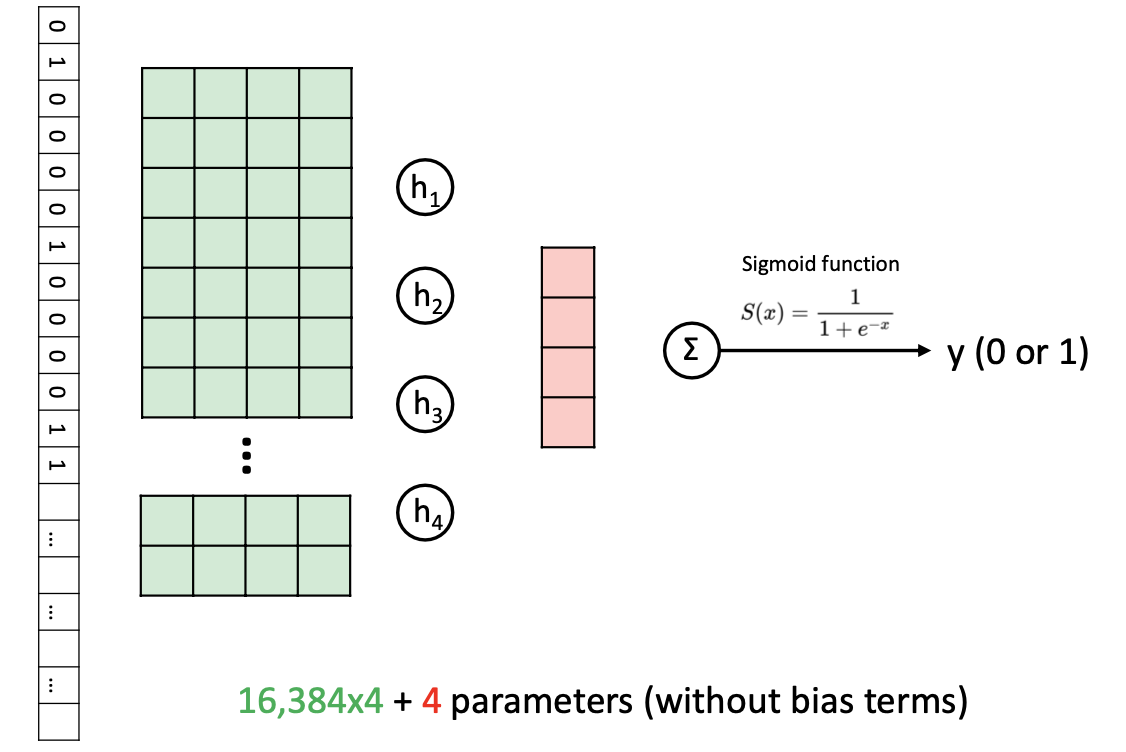
모든 파라미터의 값을 estimate해야한다.

Training

MLE principle을 사용한다.
gradient descent로 NLL을 minimize한다.

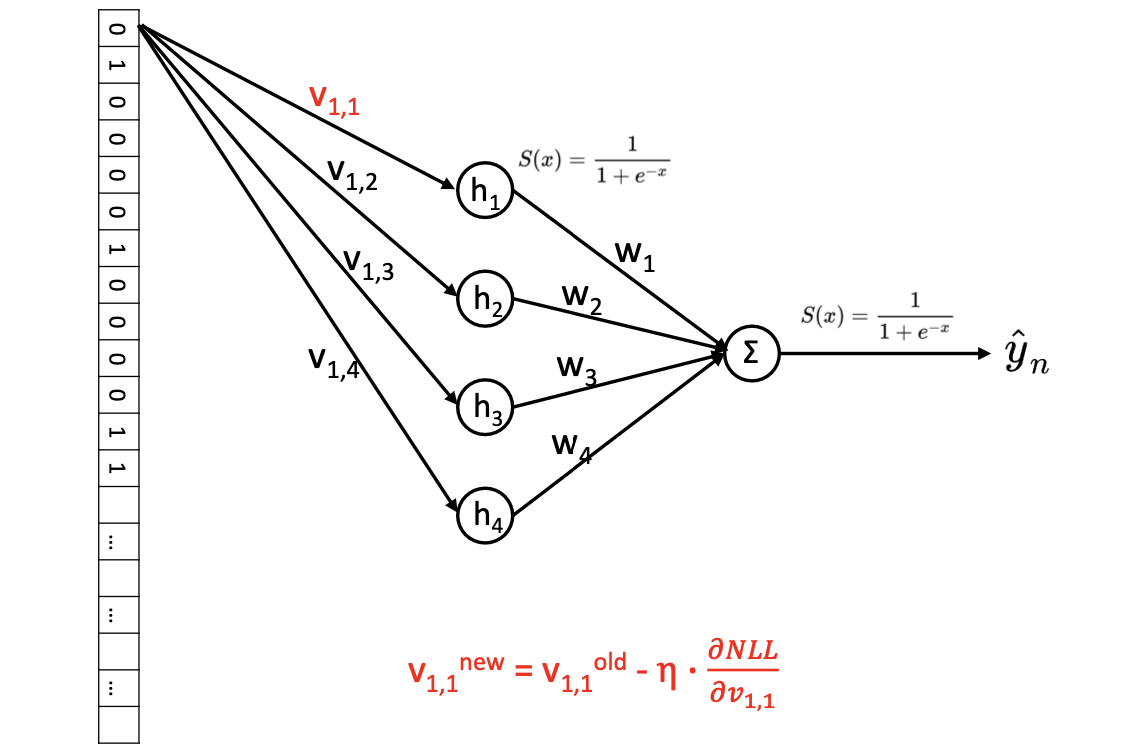
Updating $w_{1}$
- NLL(loss function)에 직접적으로 영향을 주기 때문에 direct로 편미분하여 업데이트하기 쉽다.
Updating $v_{1,1}$
- NLL이 직접적으로 $v_{1,1}$ 에 의해 결정되는 것이 아니기 때문에 chain rule을 사용해야한다.

Backpropagation

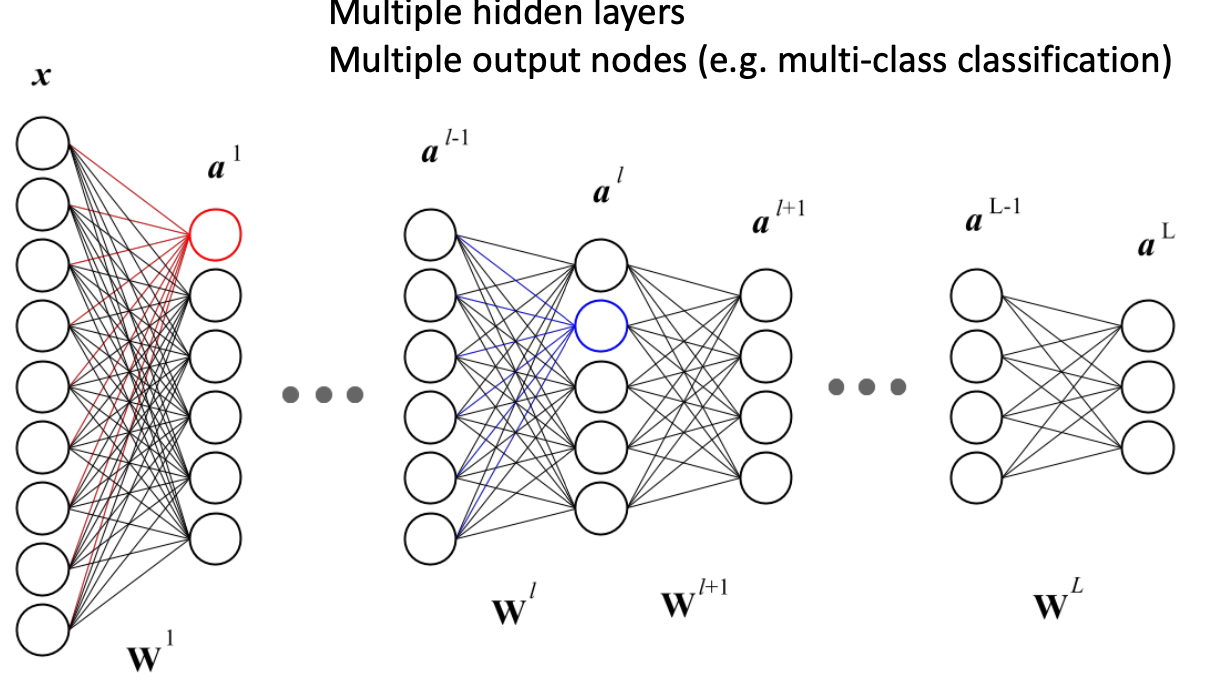
input-output pair (x,y)가 주어졌을 때의 loss
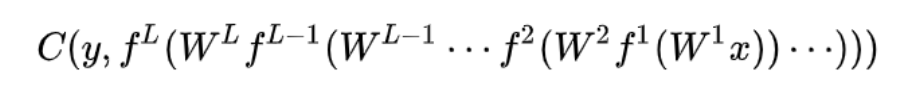
- y : ground truth label
- predicted label ŷ 은 function of nested function으로 쓸 수 있다.
- Binary classification을 하고싶으면 마지막 activation function은 sigmoid function이어야 한다.

🔗 One specific hidden layer를 자세히 살펴보자

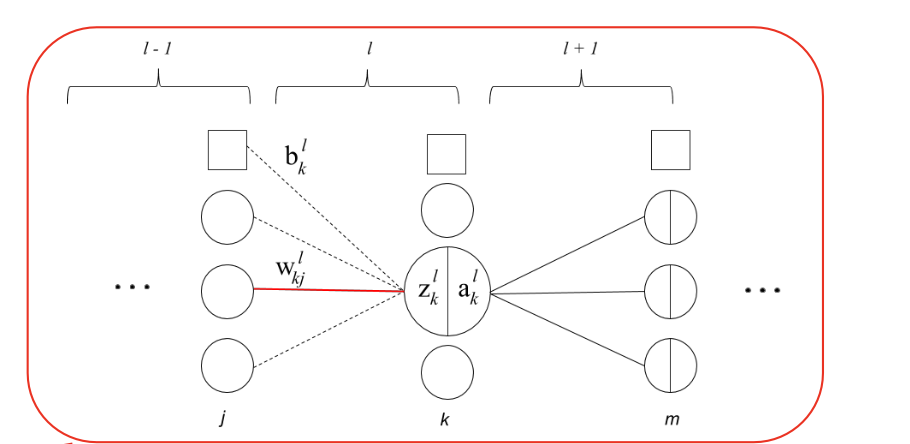
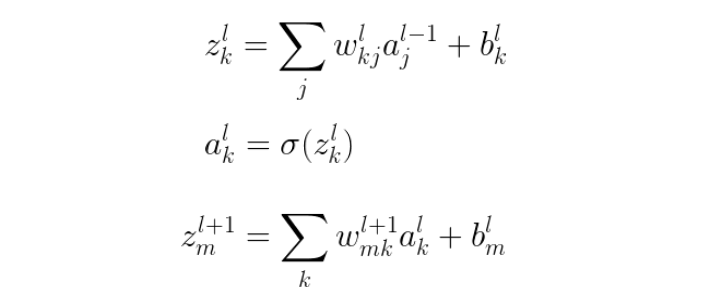
🔗 Derivative of the loss function C w.r.t. input x

⭐️ Delta

layer 전체에 대한 delta representation
- l번째 layer에서 시작하여 마지막 cost function gradient까지 올라가면서 축적된 error가 l번째 delta이다.
l번째 layer에서의 one specific neuron

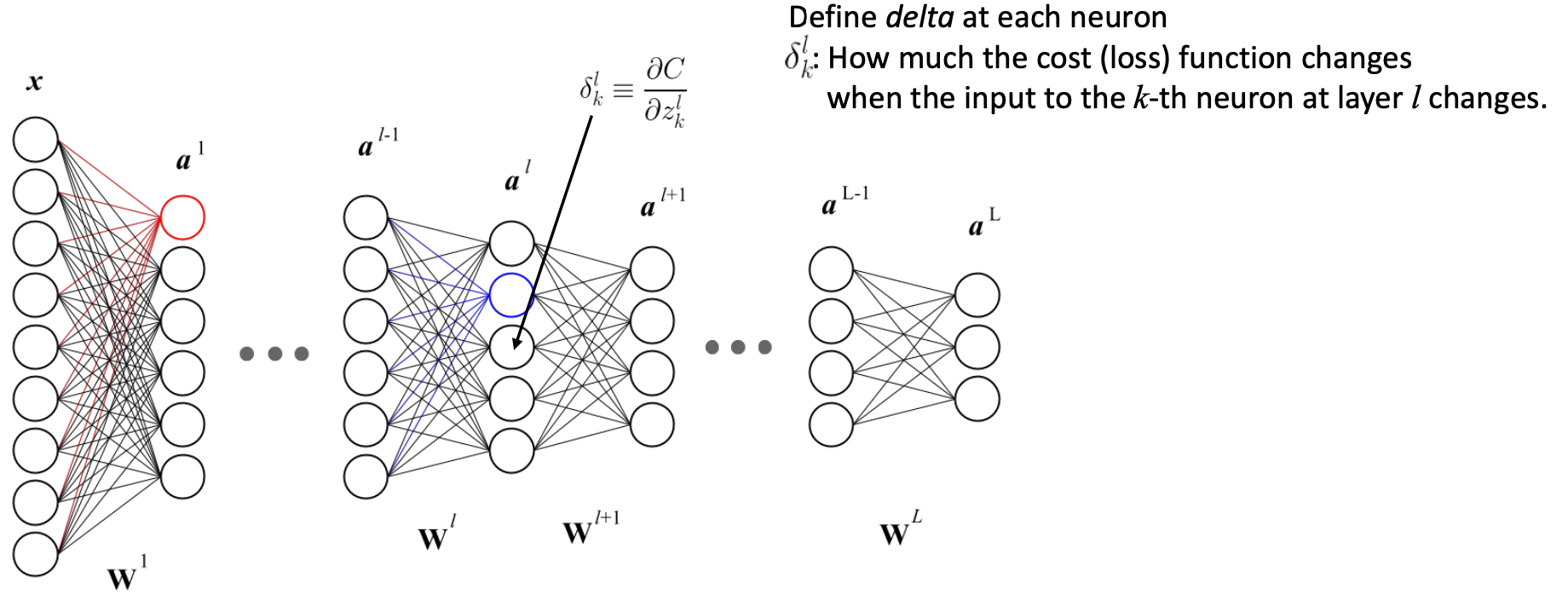
🔗 Backpropagation을 하는 이유

배경 : l번째 delta와 l-1번째 delta간에 recursive relationship이 있다. upper layer의 delta가 lower layer의 delta를 계산하는데 재사용될 수 있다.

💡 이것이 우리가 forward propagation을 하지 않고 backpropagation을 하는 이유이다.

위에서부터 시작하여(final L번째 delta) 맨 아래 (l번째 delta)까지 내려가면 이전 delta value를 재사용할 수 있다. 다시 중복해서 반복되는 term들을 계산할 필요가 없다. 따라서 forward propagation보다 backpropagation이 빠르다. 연산 낭비를 하지 않는다.
Derivative of the loss function C w.r.t. weights를 계산하는데도 delta를 쓸 수 있다. delta에 이전 layer의 output을 곱해주면 된다.
- weight를 update하는데 이것이 필요하다. Backpropagation을 통해 delta로 이것을 쉽게 구할 수 있고, parameter를 update하면서 한 layer에서 다른 layer로 이동할 수 있다.
One problem
- 계산했던 것들을 저장해야한다.
- 그래도 f같은 경우는, 만약 sigmoid function을 사용하여 derivative of sigmoid function이 이미 정해져 있기 때문에 function으로 기억하면 된다.
- 하지만 activation value는 hidden layer에 저장이 되어있어야 한다. 전체 neural network에 있는 모든 neuron의 activation value들을 다 저장해야한다. 이것이 backprop을 할때 gpu에서 많은 vram을 잡아먹는 이유이다.
- 또한 Adam, Adagrad, Adam w와 같은 advanced optimization algorithm을 사용하면 activation value뿐만 아니라 더 많은 것을 저장해야한다.

Autograd (in Pytorch)

Pytorch library가 backpropagation을 해주는 것을 autograd라고 한다.
Neural network는 주로 Directed Acyclic Graph로 표현되어있다.
- 각 node는 mathematical operation과 그 derivate를 둘 다 포함하고 있기 때문에, pytorch에서 새로운 operation을 정의하고 싶으면, operation과 그것의 derivative를 둘 다 정의해야한다.
Error signal이 output nodes에서 input nodes로 전파된다.

🔗 Example

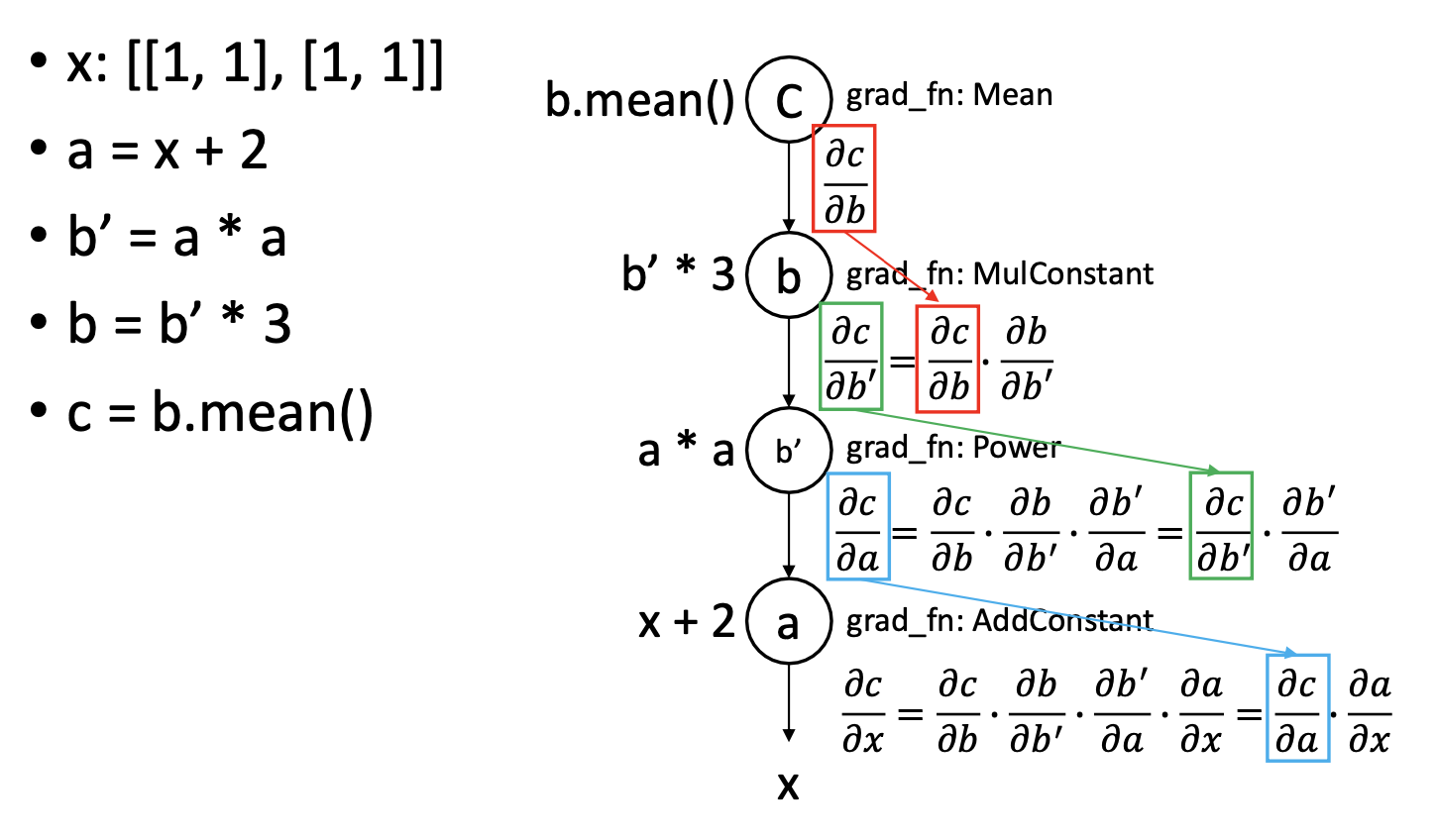
✔️ 각 grad_fn는 forward와 backward를 가지고 있다.

Forward
- Forward propagation을 계산한다.
- Backprop을 위해 Input과 activation output value를 저장한다.
Backward
- l번째 delta가 주어졌을 때, l-1번째 delta를 계산한다.
- 만약 node에 learnable parameter w가 있으면 derivative of the loss function C w.r.t. weights를 계산한다(위에서 봤던 식 사용). 그리고 parameter를 update한다.

Reference

AI504: Programming for AI Lecture at KAIST AI

이채연

AI researcher

이전 포스트

[AI504] Class 02: Basic Machine Learning

다음 포스트