[AI504] Class 10: Transformer

Self-Attention

• 2017년 Transformer 탄생
• Machine Translation의 속도를 높이기 위해 나왔다.
• 그동안의 RNN-based Encoder, Decoder는 for loop때문에 time complexity가 높았다.
• Self-Attention은 for loop를 돌릴 필요가 없고 parallelly process하기 때문에 속도를 높인다.
• Attention만 이용하여 sequence를 다룬다.

🔗 Self-Attention

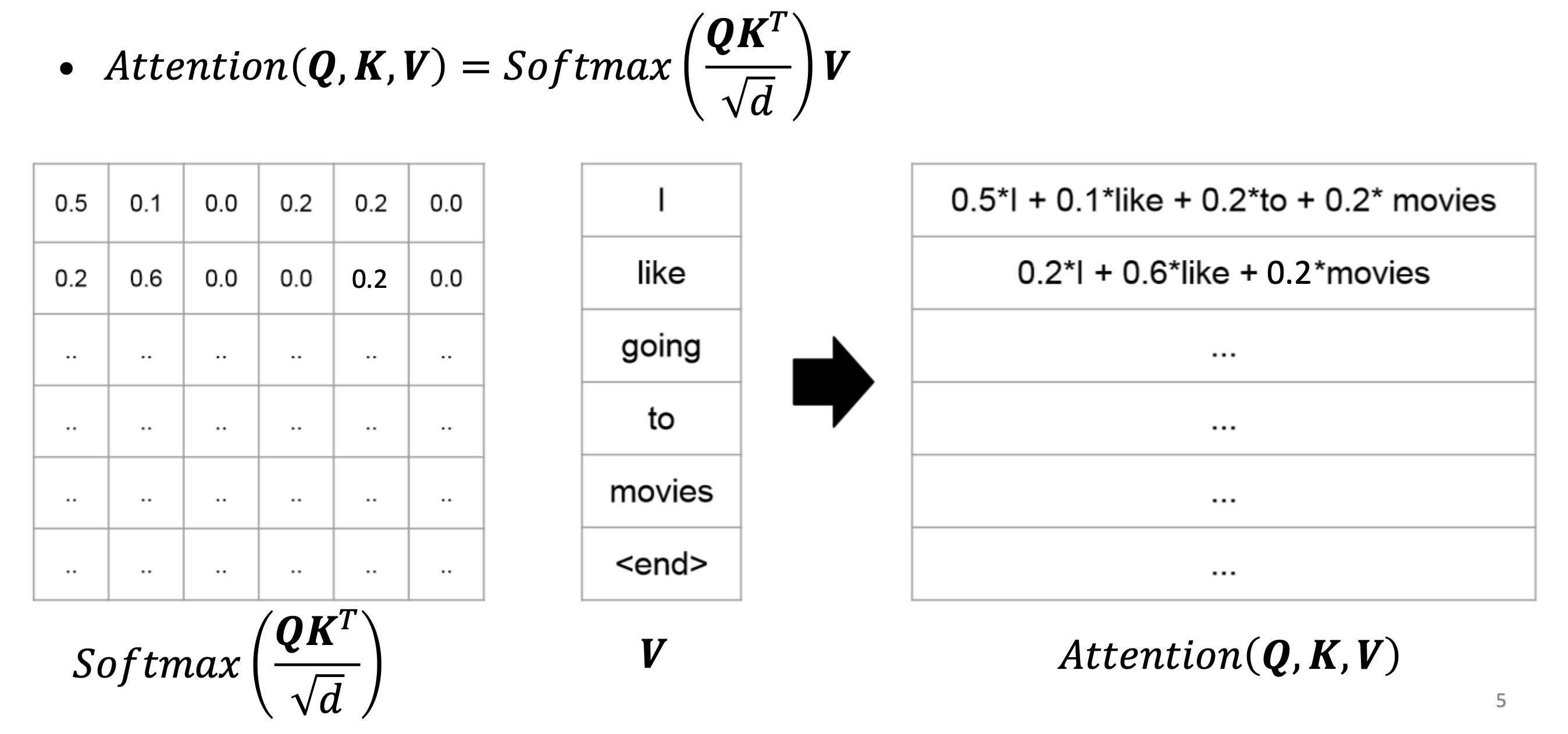
QKV operation 또는 scaled dot product라고 불린다.

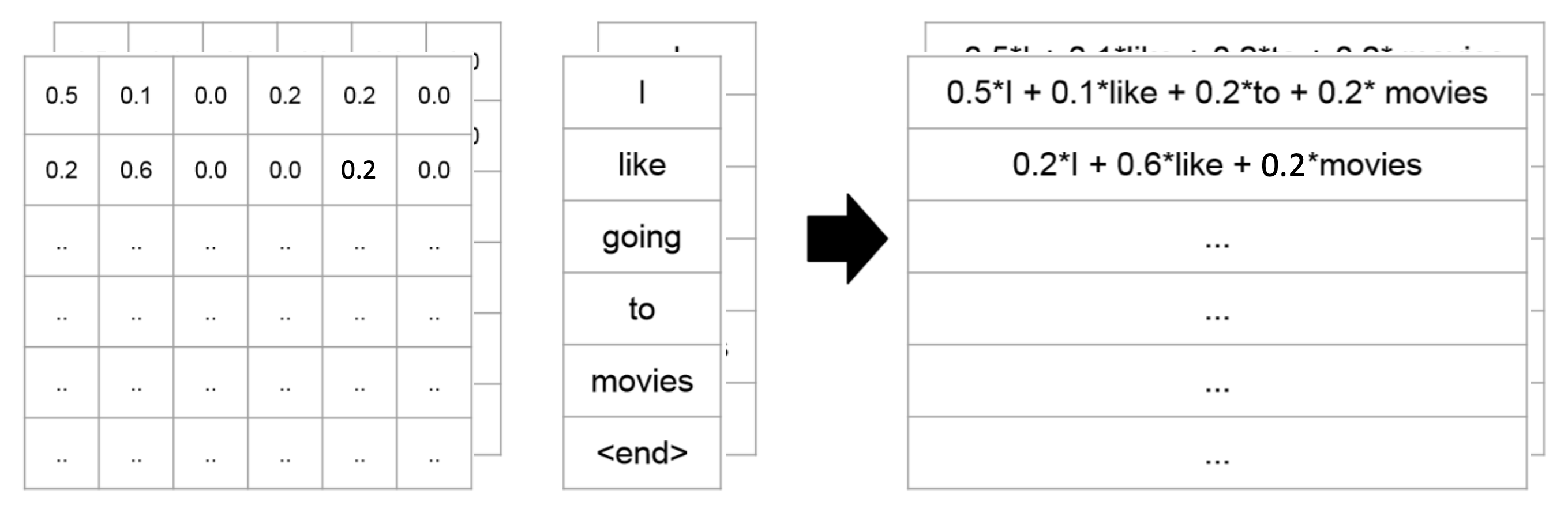
• Attention matrix를 보면, 각 row의 합이 1이다. 각 row는 attention distribution이다.
  • Softmax가 row-wise로 normalize하기 때문이다.
• Attention matrix의 첫 번째 0.5는 "I"가 자기 자신을 어떻게 생각하는 지에 대한 의미를 담고 있다.
• V의 각 row는 word-embedding이다.
• Attention(Q,K,V) matrix는 neigbor를 고려하여 mix된 contextualize/mixed-up representation이다.

🔗 QKV Operation

• "Thinking"이 main character이고 neighbor을 보는 상황이다.
• q1과 다른 ks가 서로 얼마나 compatible한지를 고려한다.
• Inner product score는 vector size가 커짐에 따라 arbitrary하게 커질 수 있기 때문에 normalize해준다.
• "Thinking"은 자기 자신과 88%의 compatibility를, "Machines"와 12%의 compatibility를 가진다.
• 0.88 * $v_1$ + 0.12 * $v_2$ = $z_1$

✔️ Vecterize form을 이용하여 모든 words를 동시에 processing한다.

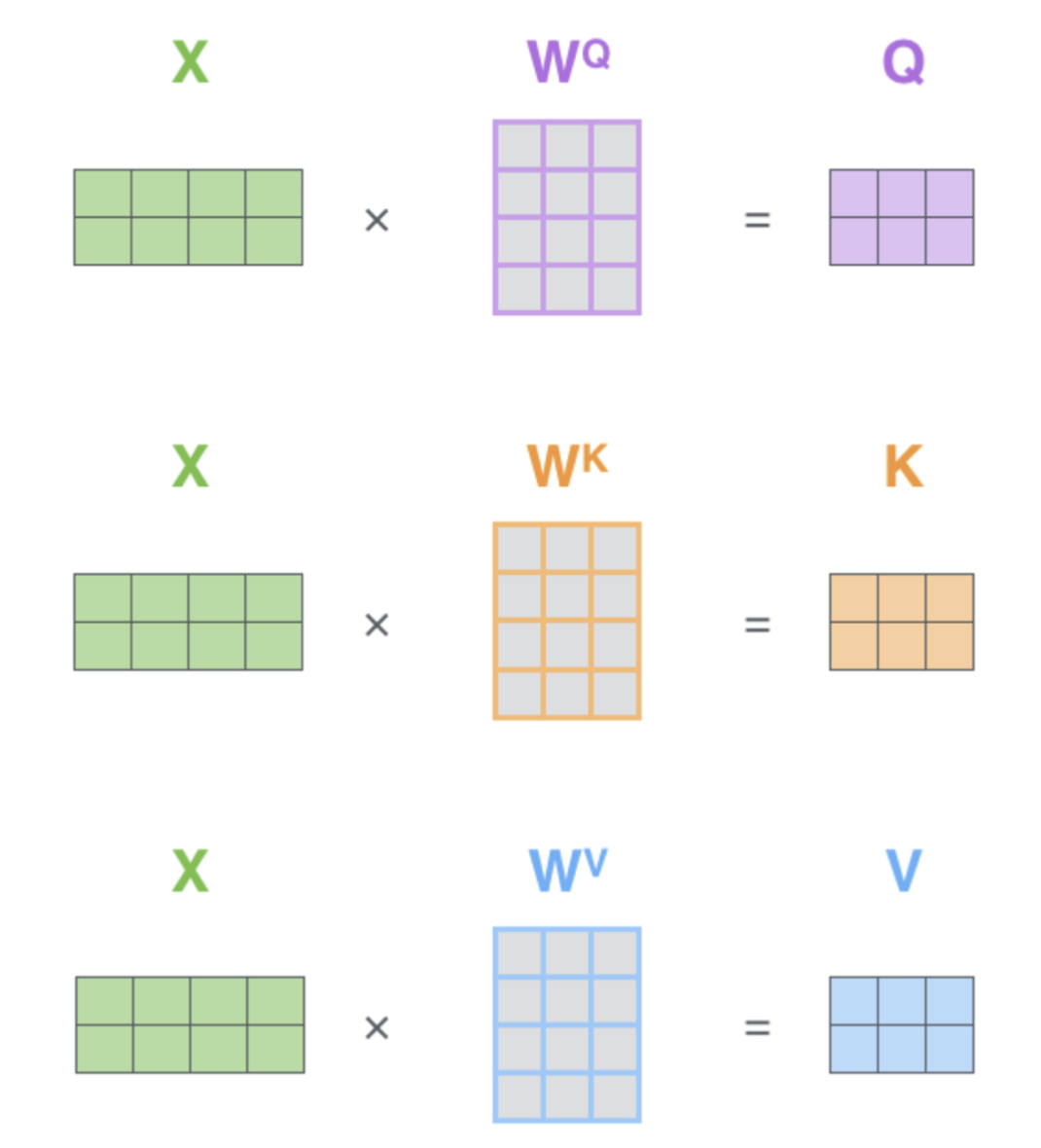
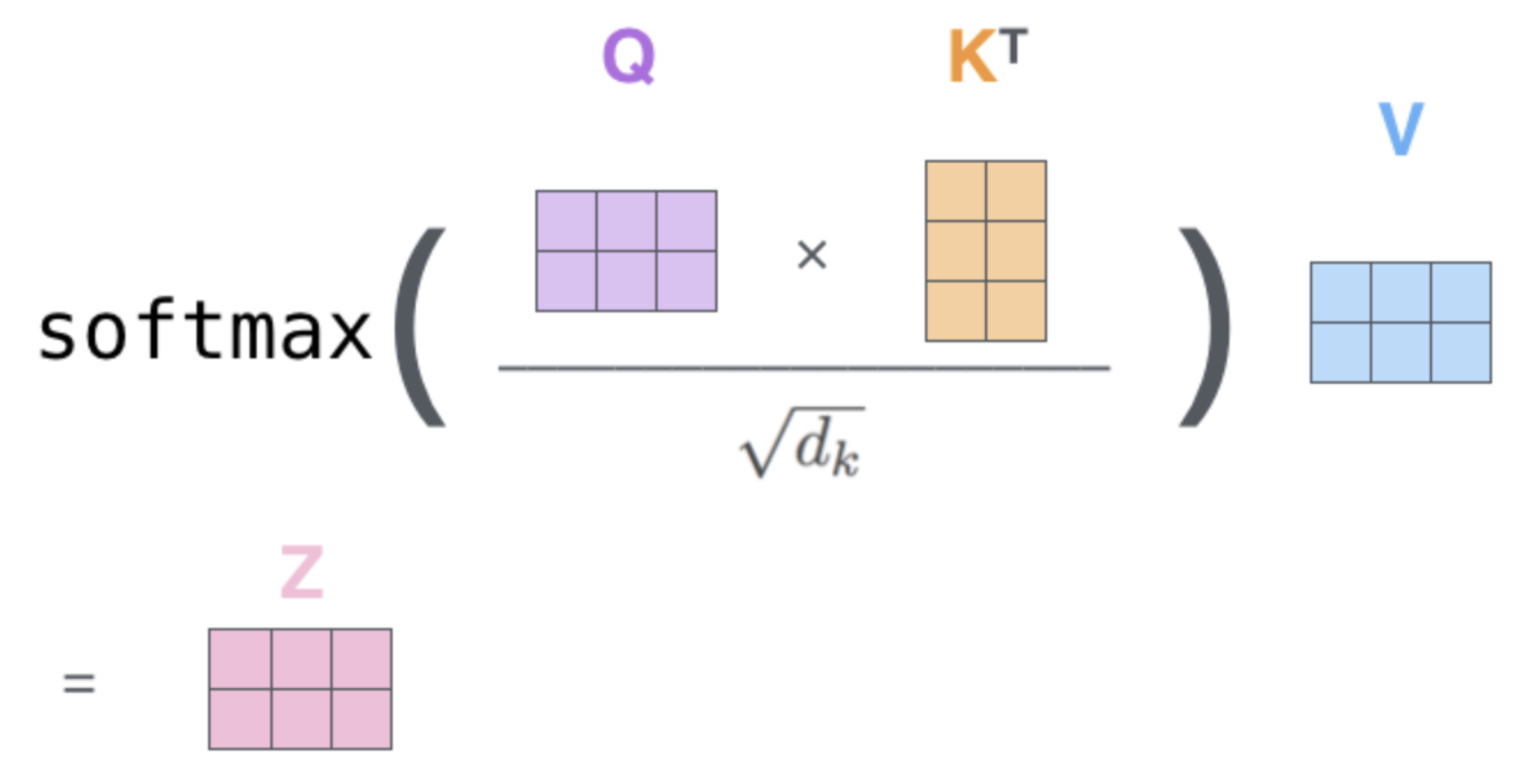
• For loop가 필요없고 parallel하게 동작하기 때문에 powerful한 GPU가 있으면 매우 매우 속도가 빠르다.

Multi-head Attention

💡 Motivation
Language를 이해하기 위해서는 1개 이상의 attention matrix/weighted sum이 필요하다.

• 현재는 fixed된 양의 parameter/resource를 여러 attention head에 분산시킨다.
• Original Transformer paper에서는 learnable parameter를 늘렸다.

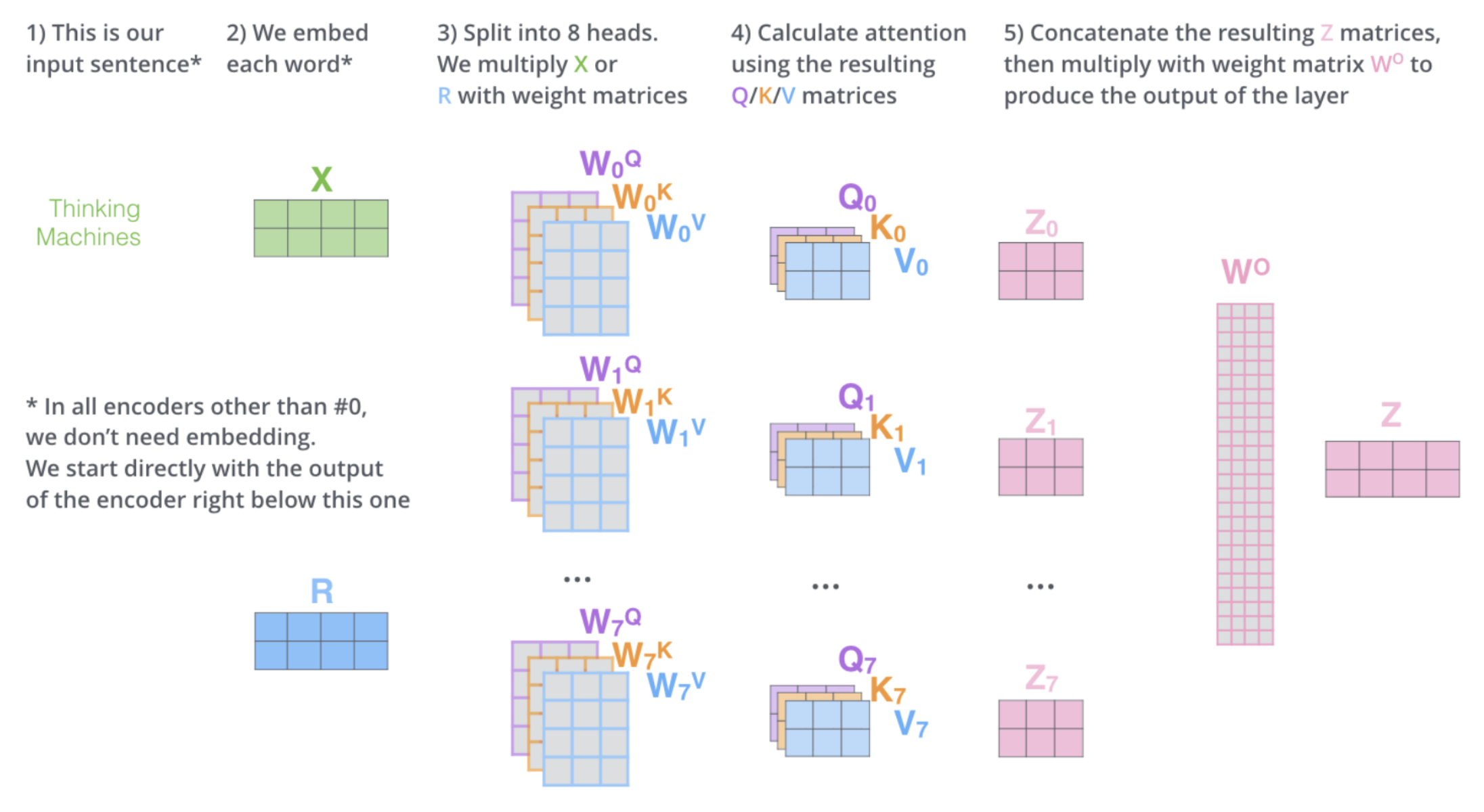
🔗 Visualizing the Attention

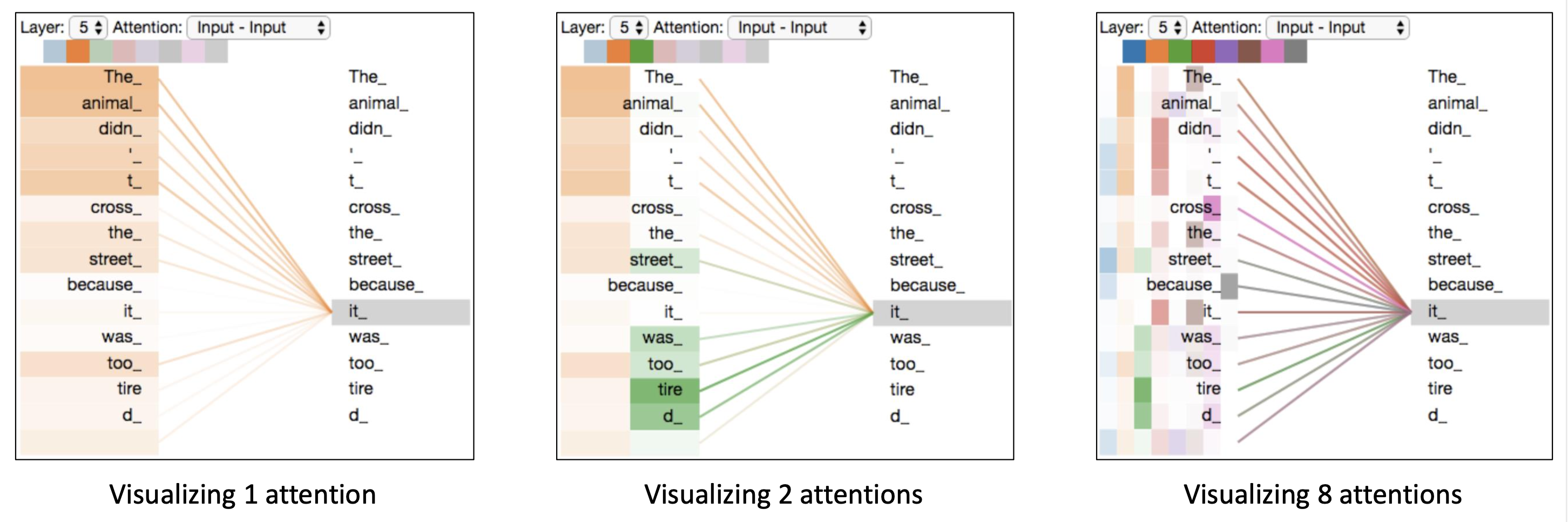
• 총 6개의 layer가 있고 각 layer마다 8개의 attention head를 가지고 있다.
• 각 head가 서로 다른 역할/목적을 수행한다는 것을 볼 수 있다.

Transformer (Encoder)

🔗 Transformers

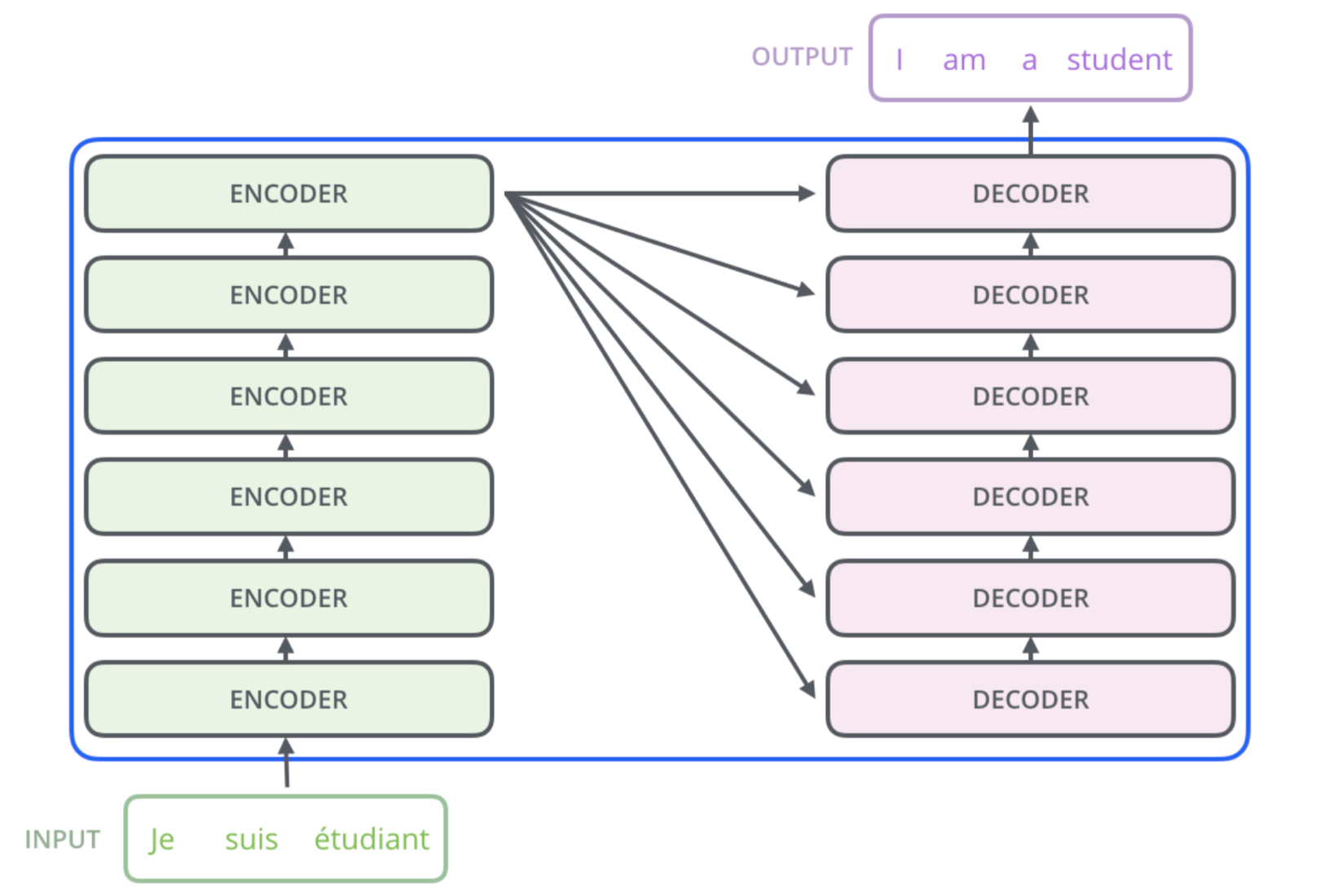
• input token 개수 = output token 개수
• Layer에 대한 for loop는 있지만 sequence에 대한 for loop는 없다.

🔗 Encoder, Single Block

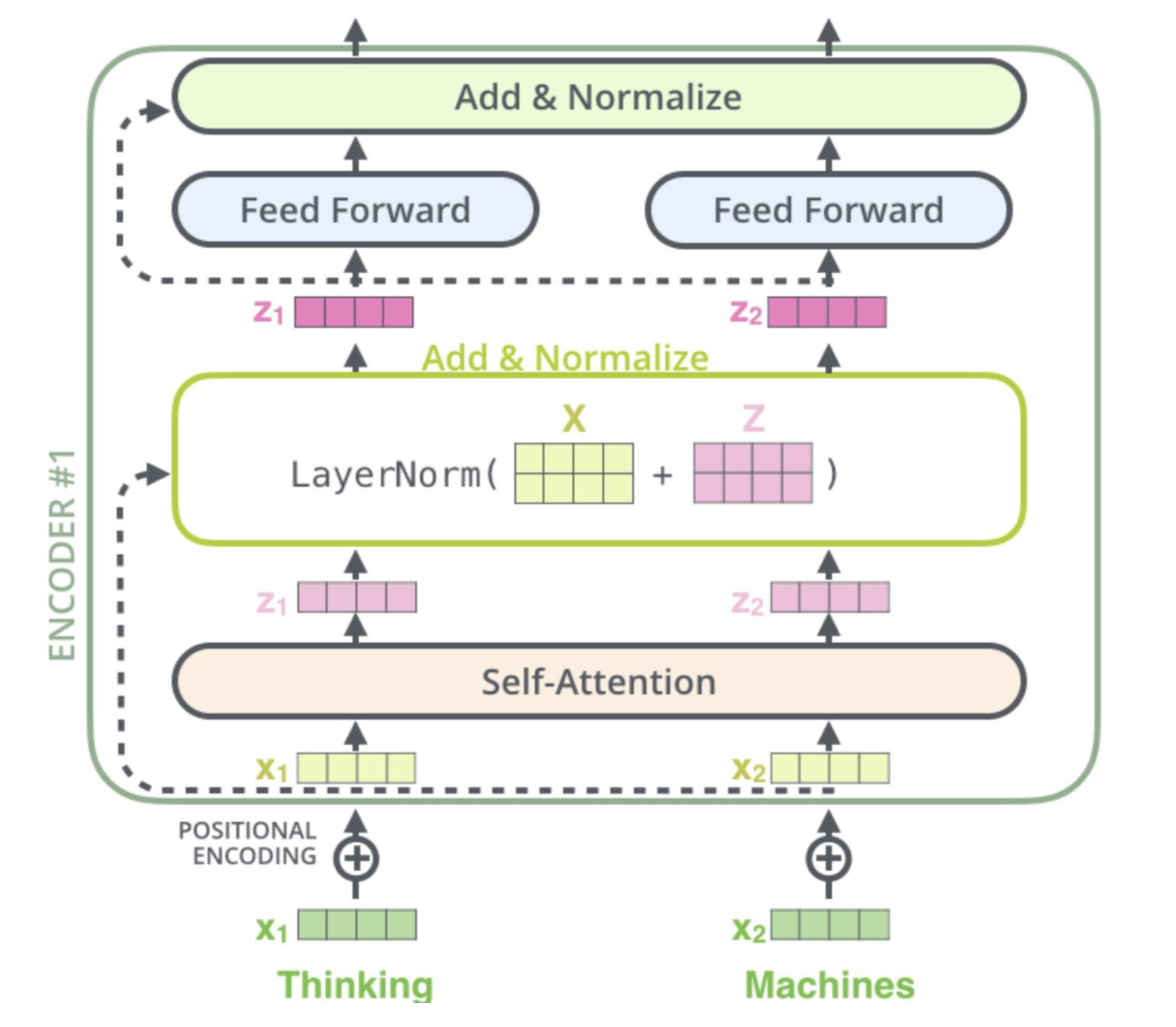
• Input(words) -> Self-attention (QKV Op) -> MLP -> Output
  • Feed-Forward Neural Network : non-linearity를 주기 위해서이다.
• Residual Connetion (from ResNet)
• Layer Normalization

Positional Encoding

🔗 Motivation

• Self-Attention = Set Encoding
  • Self-Attention은 purely data driven방식이며, 이것이 transformer가 powerful한 model인 이유이자 매우 많은 양의 데이터가 필요한 이유이다.
• Model이 sequence를 다룬다는 것을 알게하고 싶어, position마다 content가 바뀌어야 한다.
• 그래서 model에 order information을 넣어주고자 positional encoding을 한다.

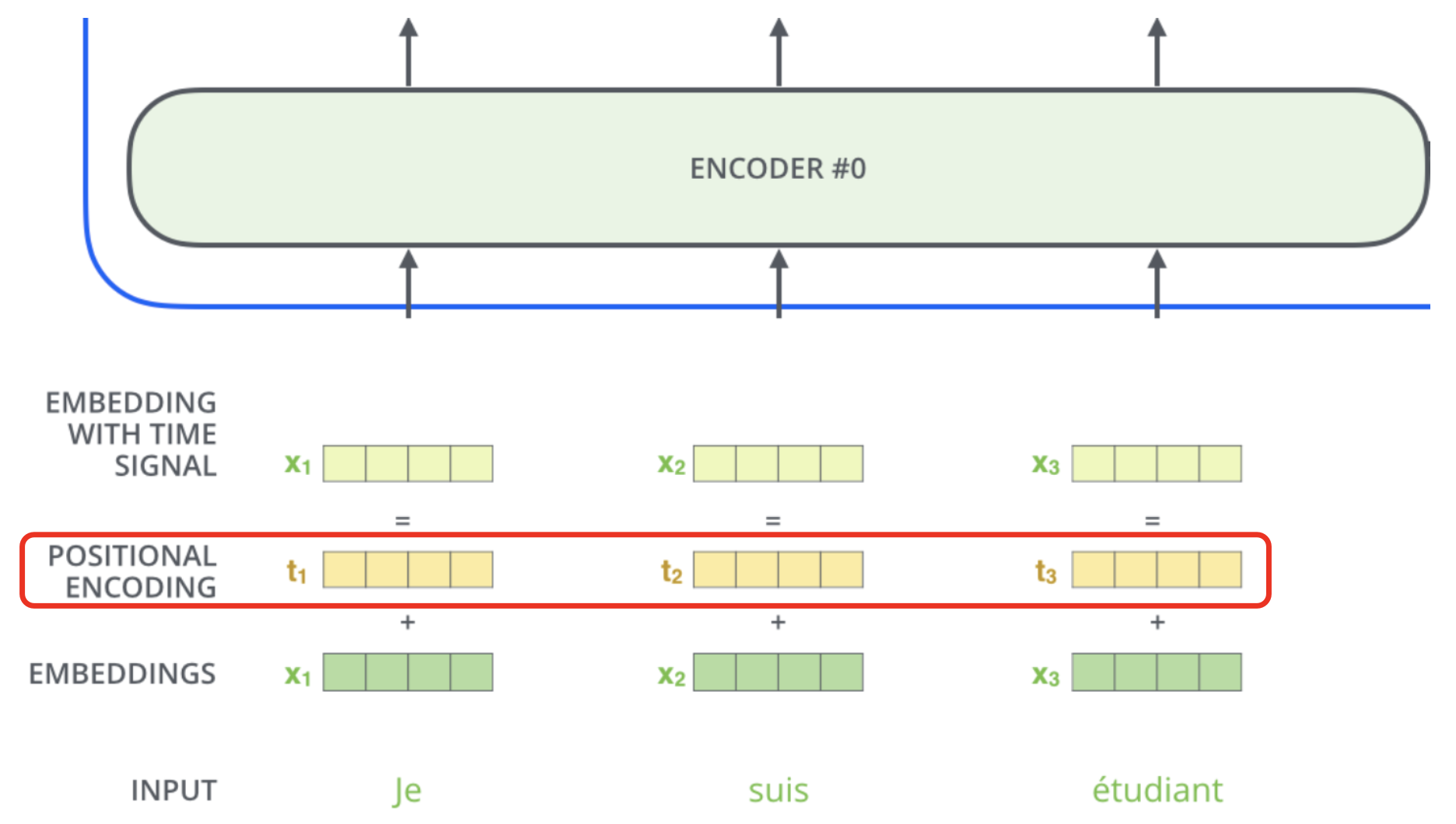
🔗 Position Encoding Requirement

• 각 time step(position)마다 unique encoding을 output해야한다.
• 두 time step 사이의 거리는 길이가 다른 문장 전체에 걸쳐 일치해야 한다.
• Model은 긴 문장으로 잘 generalize되어야 한다. 값은 제한되어야 한다.
• Deterministic해야한다.

🔗 Naive Examples

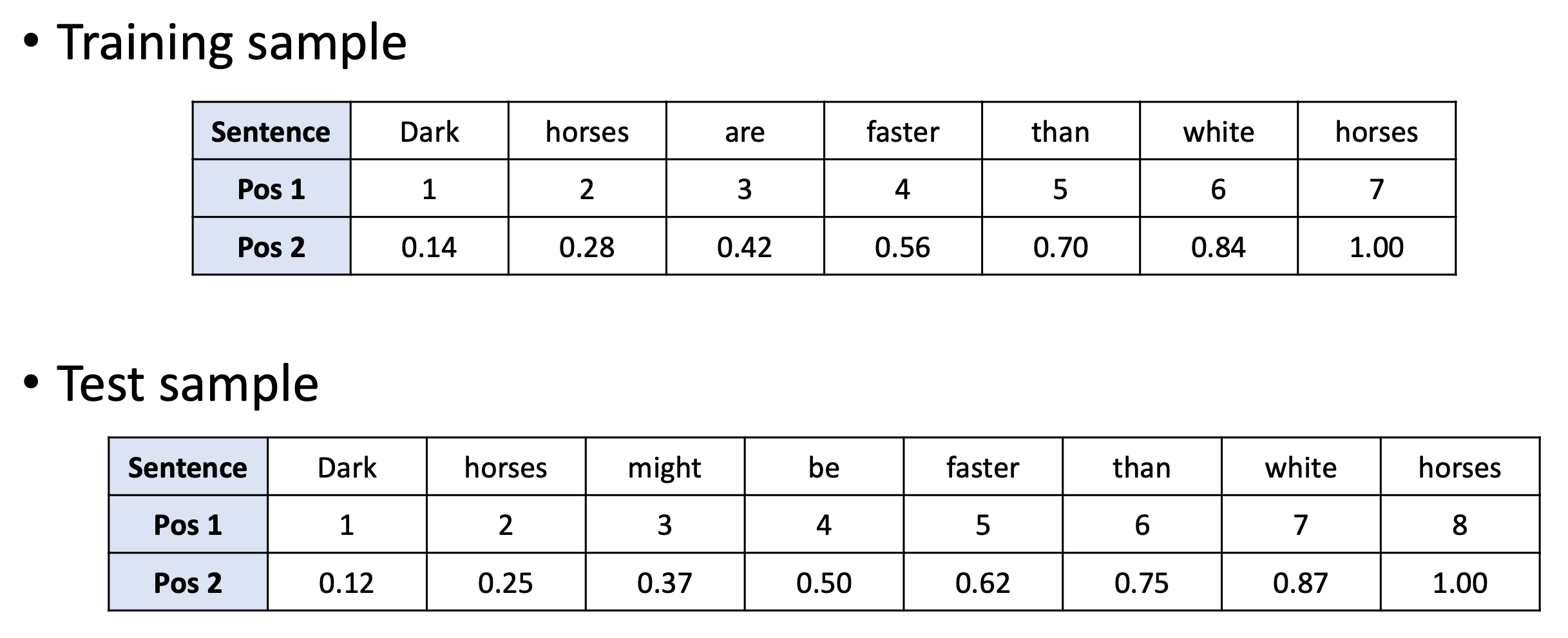
• Strategy1 문제 : 더 긴 문장을 만나면 못본 숫자가 나오게 된다.
• Strategy2 문제 : 더 긴 문장을 만나면 값이 살짝 바뀐다.

🔗 Discrete Example - Use binary values

• Scaler value 말고 vectorize form을 사용
• Dimension마다 frequency가 다르다.
  • 이 성질이 sin함수와 cos함수를 사용하여 continuous form으로 확장된다.
• 문제 : Binary values waste space.

🔗 Continuous Encoding - Use sinusoidal functions

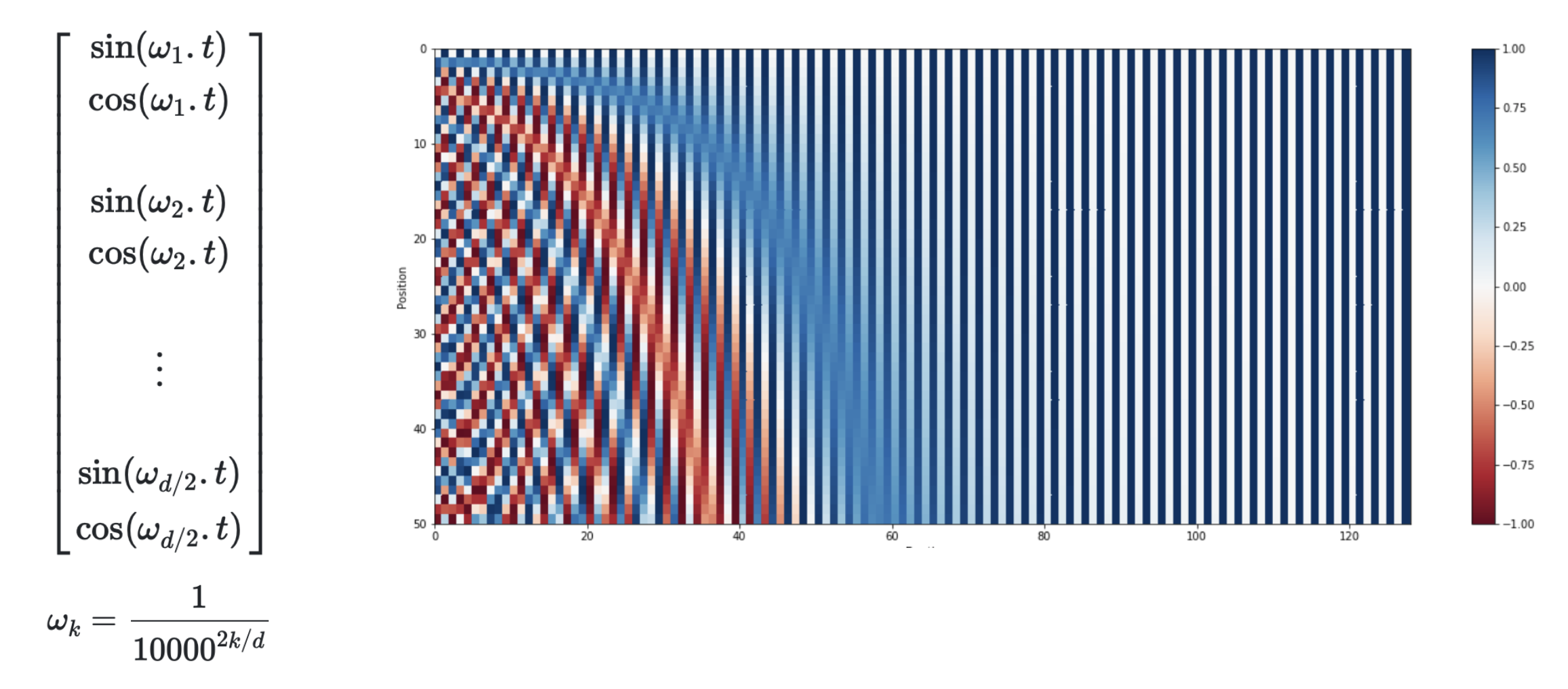
• Continuous function을 사용하여 각 dimension마다 다른 frequency를 적용한다.
  • 처음 dimension은 value가 자주 바뀌고, 뒤로 갈수록 덜 자주 바뀐다.
• 하나의 sin, cos쌍마다 같은 frequency를 적용한다.

Sequence-to-Sequence

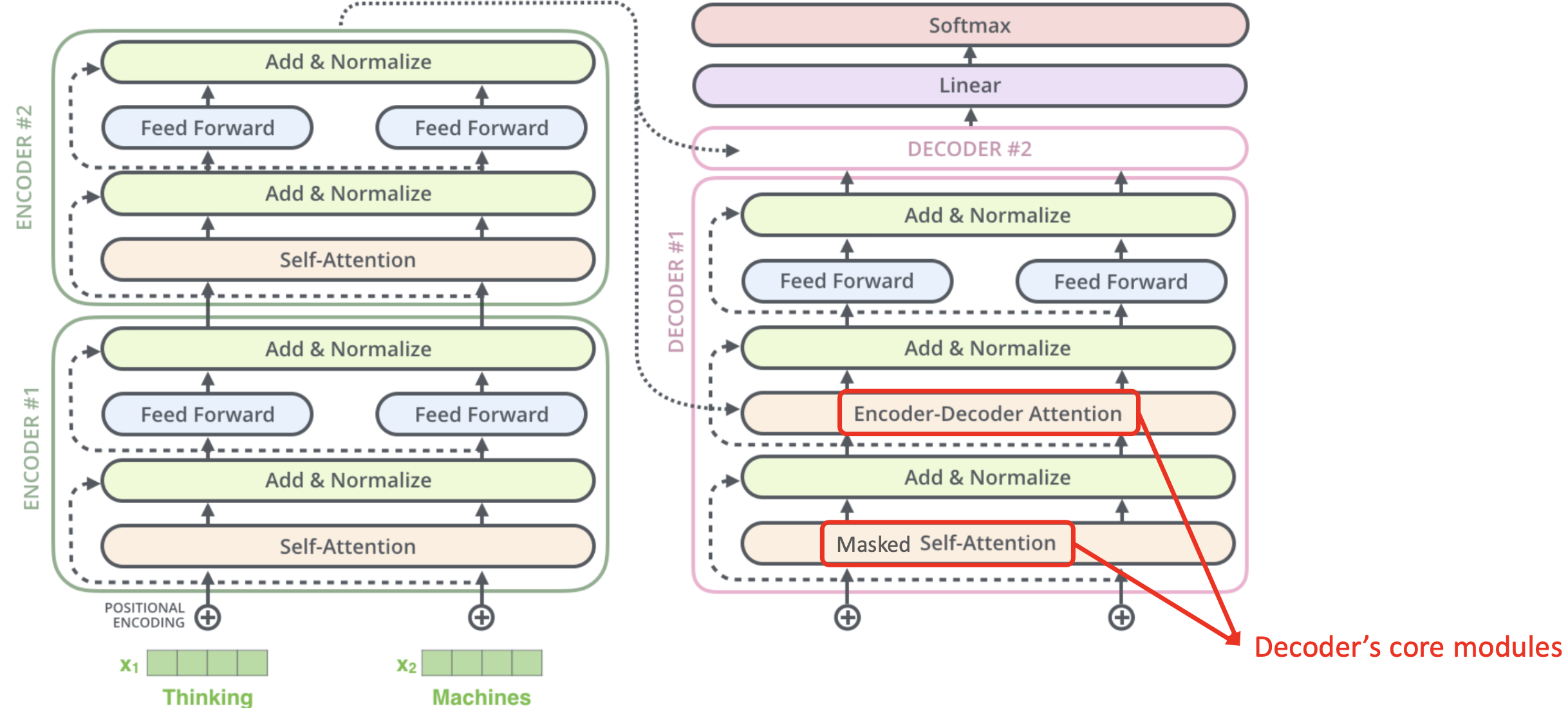
• End-to-end process

Decoding Process

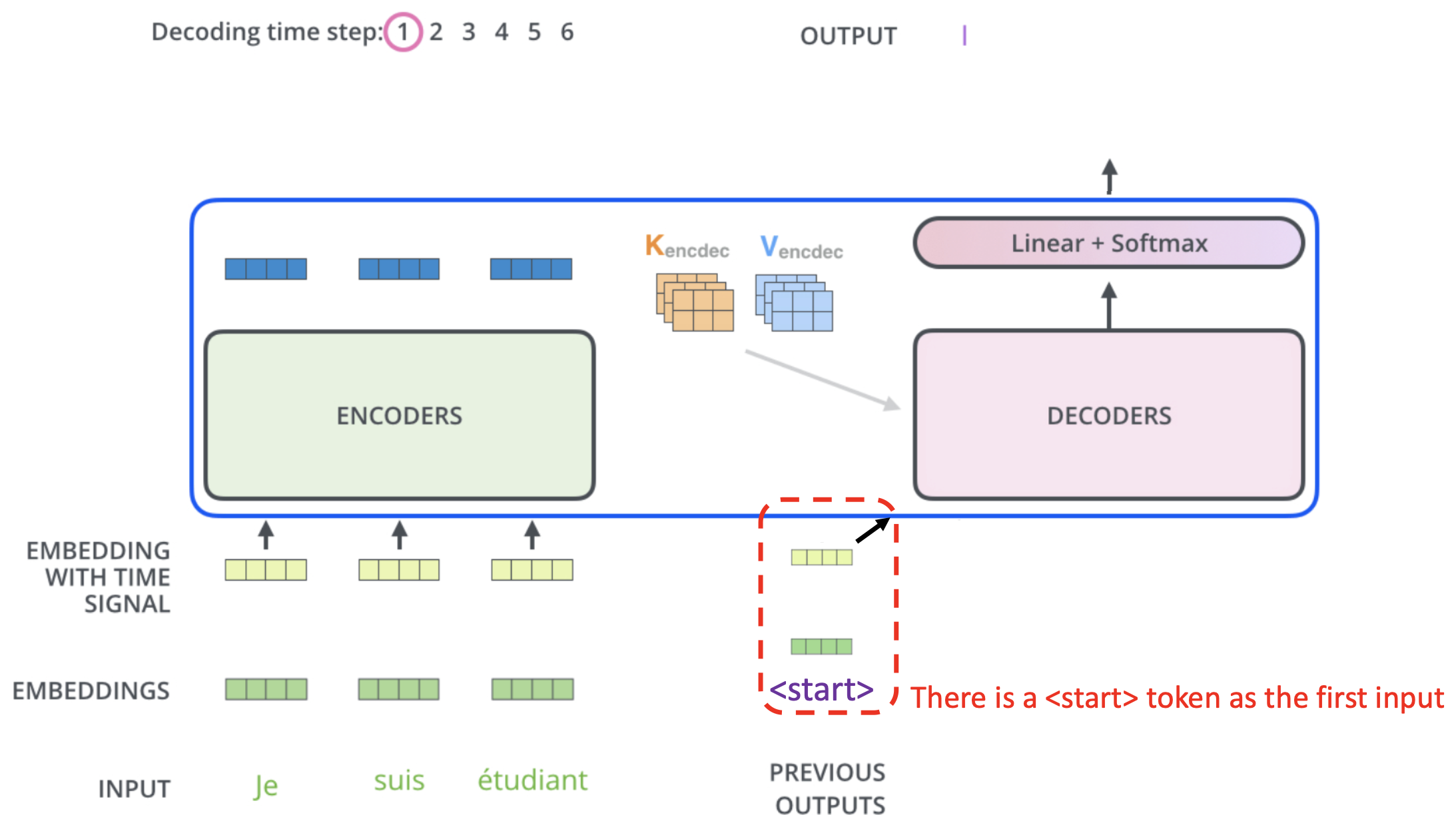
Prediction Layer

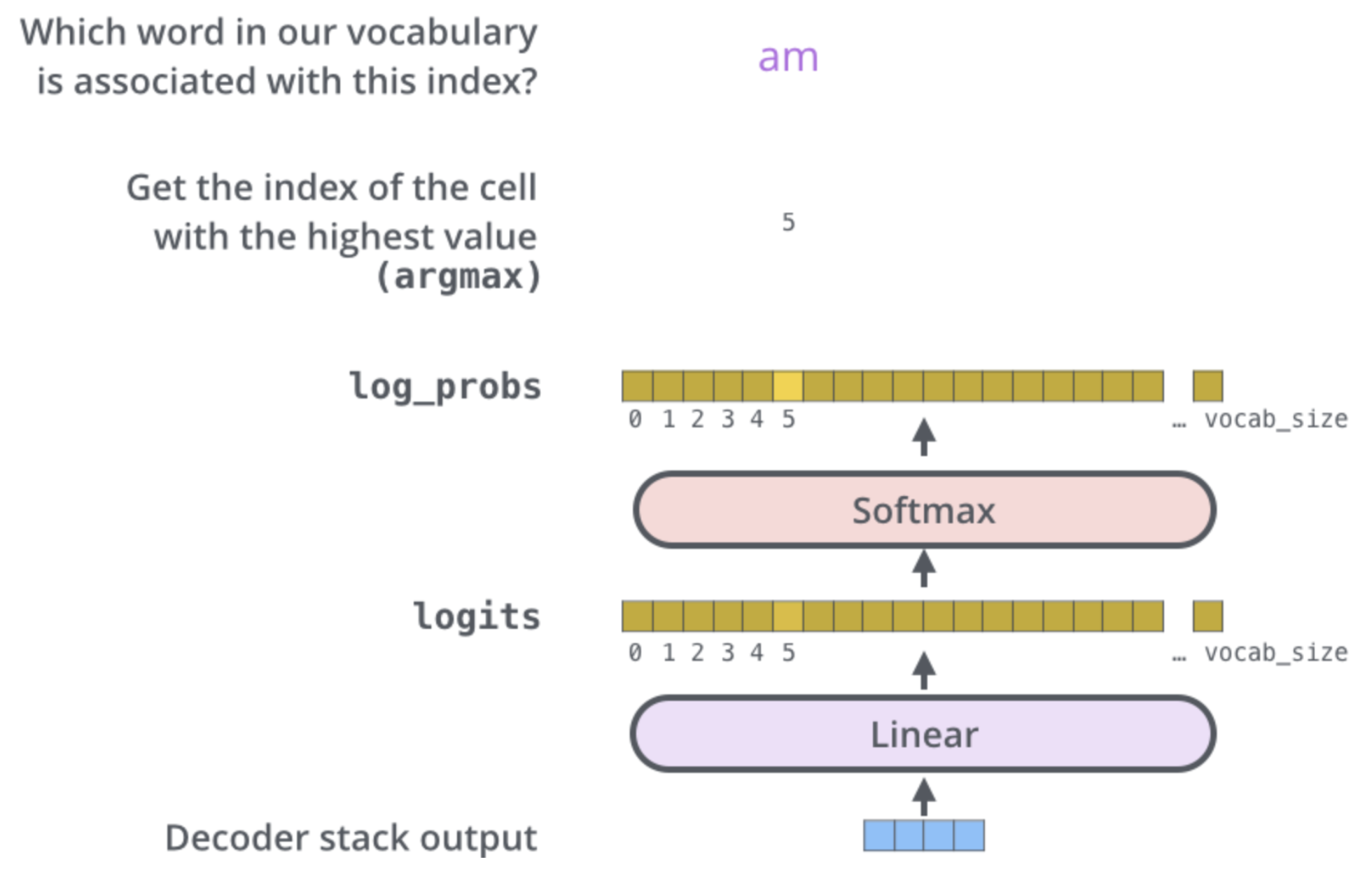
• 매 time step마다 어떤 word로 predict할지 결정한다.

Encoder-Decoder Attention

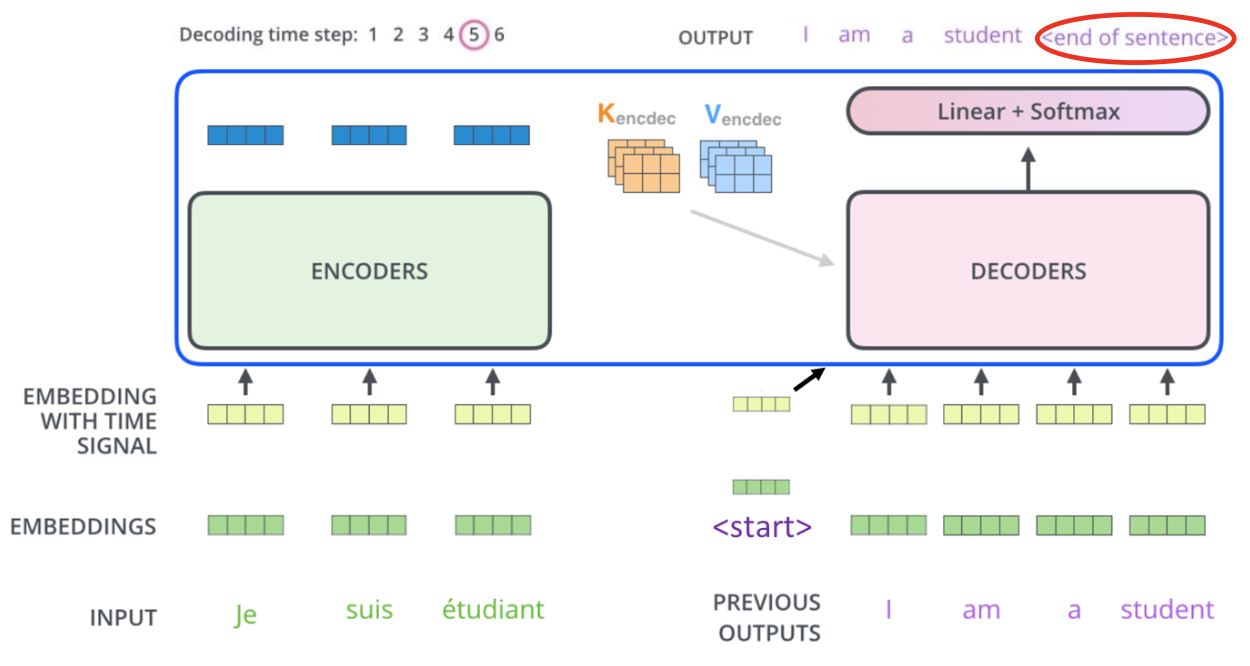
• Decoder input으로 querys를 생성한다.
• Encoder의 모든 output으로 keys와 values를 생성한다.
• query와 key로 score를 구하고 softmax를 적용해서 나온 probability로 values를 sum한다.
  • Attention matrix : (decoder에서 input token 개수) X (encoder에서 output 개수)

✔️ Decoding during Training & Testing

• Training phase

  • Ground truth word를 decoder의 input으로 집어넣기 때문에 모든 query들을 한번에 process할 수 있다.
  • Encoder에서처럼 matrix operation을 한다.
  • For loop이 없다.

• Testing phase

  • Ground truth를 모르기 때문에 한번에 한 token씩 generate한다.
  • Autoregressive generation
  • For loop이 필요하다.
  • Future를 볼 수 없다.

➡️ 이러한 training phase와 testing phase의 차이 때문에 동일하게 맞춰주고자 training phase에서도 future를 볼 수 없게 한다. 이렇게 cheating을 방지하게 위해 decoder에서는 Masked Self-Attention을 사용한다.

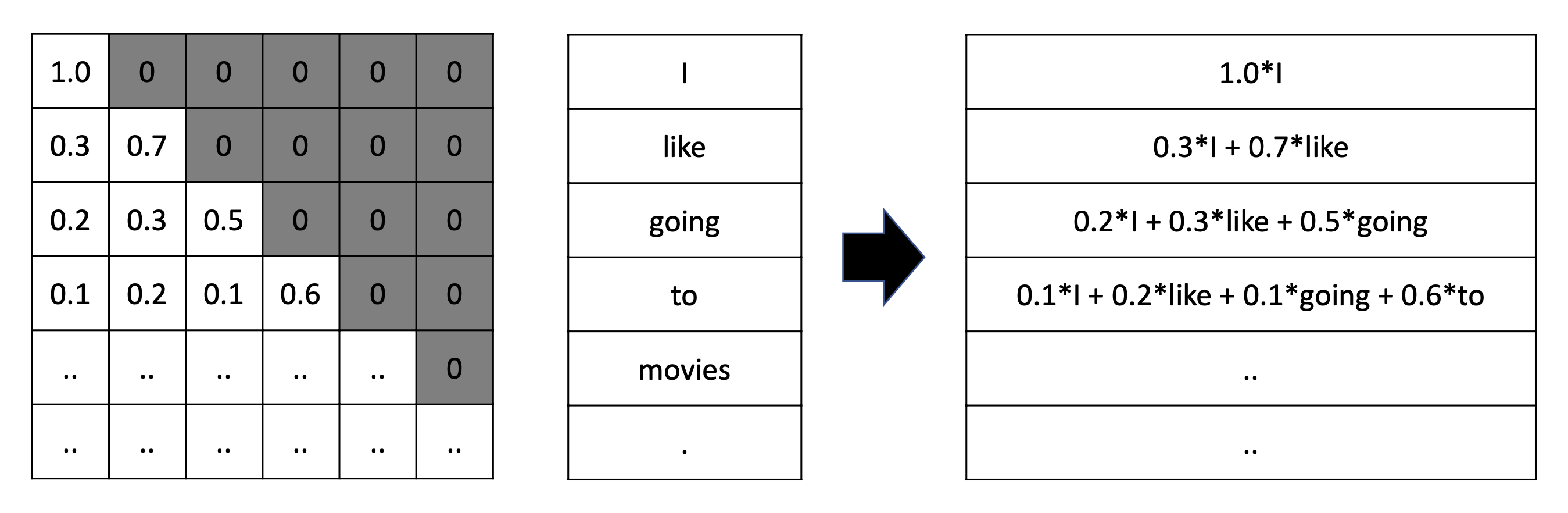
Masked Self-Attention

• 각 token은 자기 자신과 왼쪽(backwards)만 볼 수 있다.

🔗 Masked QKV Operation

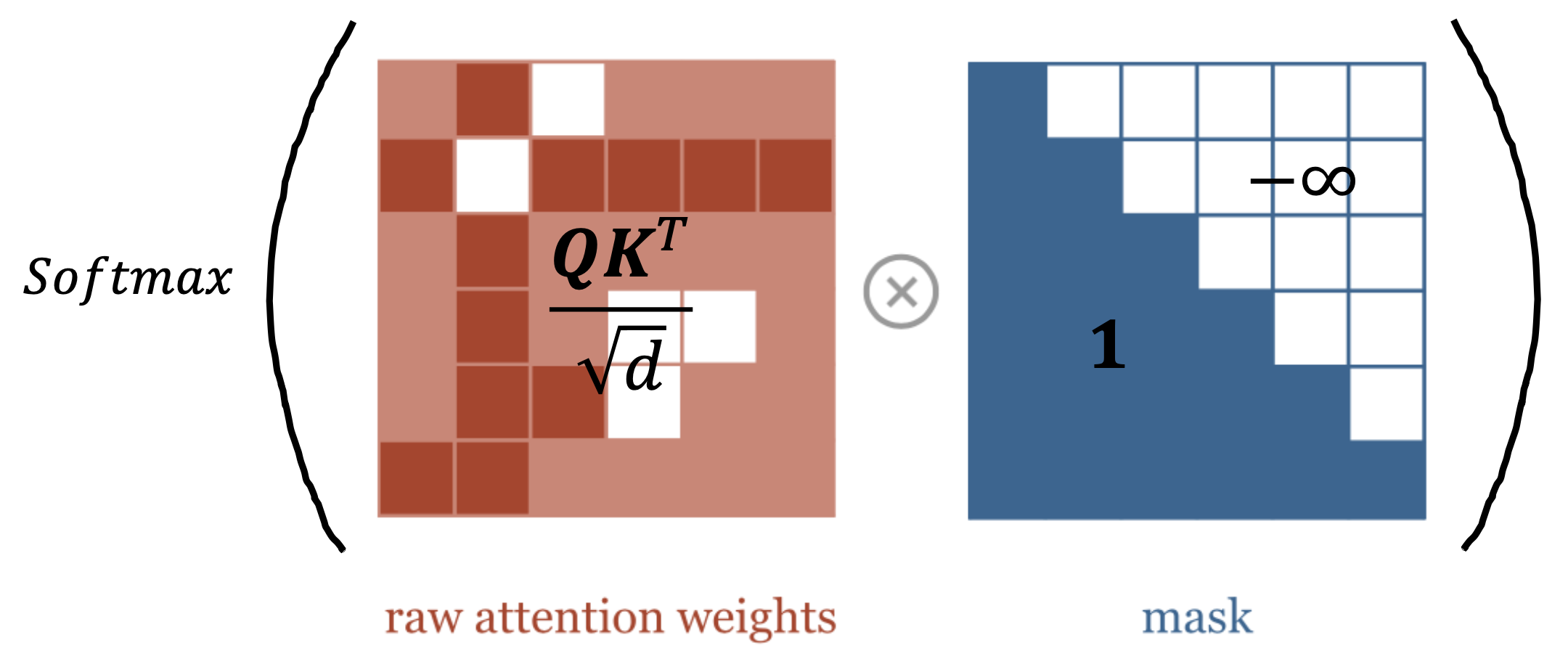
• Unnormalied attention에 softmax를 적용하기 전에 triangular matrix인 mask를 multiply한다.
  • -∞가 softmax에 들어가면 zero score가 된다.

Reference

• AI504: Programming for AI Lecture at KAIST AI