Overview

1. 차원의 저주
2. 차원 축소를 위한 접근법 ∘ 사영, 다양체학습
3. PCA ∘ 분산 보존, 주성분
4. 커널 PCA
5. LLE (지역 선형임베딩)

---

많은 ML 문제는 훈련 샘플이 수백만 개의 특성을 갖는데, 샘플의 특성이 너무 많으면 학습이 매우 느리고 어려워진다. 이런 문제를 차원의 저주라고 한다.

다행히 많은 경우 특성 수를 줄여서 학습 불가능한 문제를 학습 가능한 문제로 만들 수 있고, 이러한 기법이 차원 축소이다. 차원을 축소하면 정보가 손실되어 성능이 저하될 수 있지만, 학습 속도가 빨라진다는 장점이 있다.
예를 들어 앞서 본 MNIST 데이터는 사진 중앙 부분만 인식하거나 인접한 두 픽셀을 하나로 합쳐도 충분하며, 주성분분석(PCA) 기법을 이용하여 154개의 픽셀만 대상으로 학습할 수 있음을 뒤에서 볼 것이다.

데이터 시각화에 있어서도 3차원을 초과하는 고차원의 공간은 머릿속에서 상상하기 매우 어렵다. 차원을 2,3차원으로 줄이면 그래프로 시각화할 수 있고 군집 같은 시각적인 패턴을 감지하여 데이터에 대한 통찰을 얻을 수도 있다.

1. 차원의 저주

차원이 불필요하게 높은 것은 시각화 외에도 여러 문제를 일으킨다. 고차원은 많은 공간을 가지고 있기 때문에, 차원이 커질수록 두 지점 사이의 거리가 매우 커진다. 즉, 특성 수가 너무 많으면 훈련 샘플 사이의 거리가 커져서 불필요한 과대적합 위험도가 커진다.
해결책으로는 샘플이 충분한 밀도를 갖도록 샘플 크기를 늘리는 방법이 있지만, 고차원에 충분할 만큼의 많은 샘플을 준비하는 것은 사실상 불가능하다. 따라서 차원 축소를 적절히 사용해야 한다.

2. 차원 축소를 위한 접근법

일반적으로 고차원 훈련 샘플의 경우, 모든 샘플들이 저차원 부분공간에 가깝게 놓여있는 경우가 많다. 모든 차원에 균일하게 퍼져 있기보다는, 크게 영향을 주지 않는 특성이 있거나 강하게 연관된 특성들이 있을 수 있다.
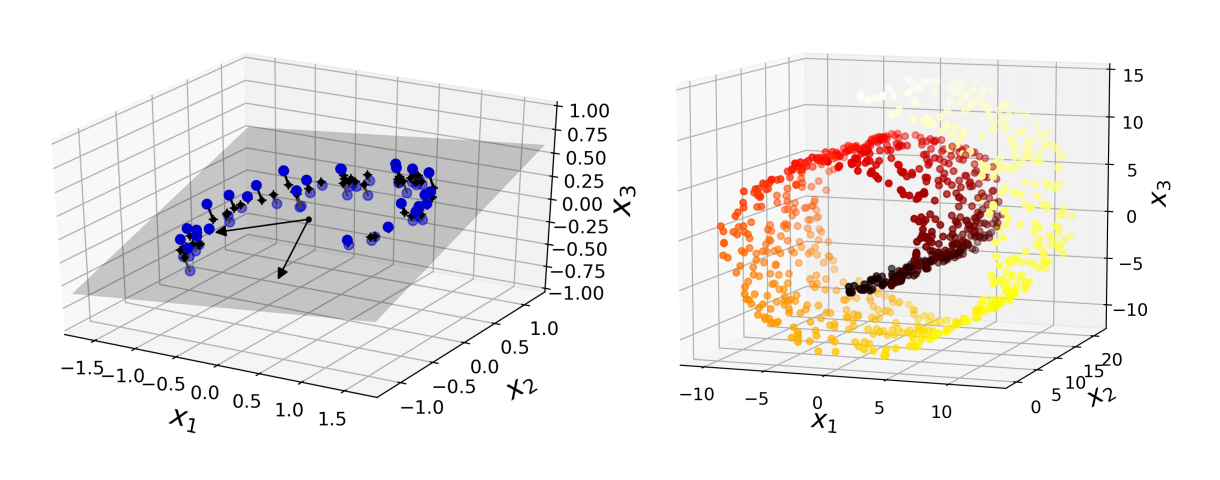
예를 들어 아래 두 이미지는 모두 3차원에 놓인 데이터를 나타내지만 왼쪽은 2차원 평면, 오른쪽은 휘어진 2차원 평면에 가깝다. 이 경우 3차원 데이터를 2차원으로 차원 축소할 필요가 있다. 대표적인 차원 축소 기법에는 사영과 다양체 학습이 있다.

사영

$N$차원 공간에 존재하는 $n$차원 부분공간을 $n$차원 공간으로 사영(projection)할 수 있다.

예를 들어 아래 첫 그림의 3차원 공간에 있는 훈련 샘플을 회색으로 표현된 2차원 평면으로 사영하면, 새로운 축 $z_1, z_2$를 갖는 2차원 데이터가 된다. 이때 새로운 축을 적절하게 찾는 것이 사영의 중요한 과제가 된다.

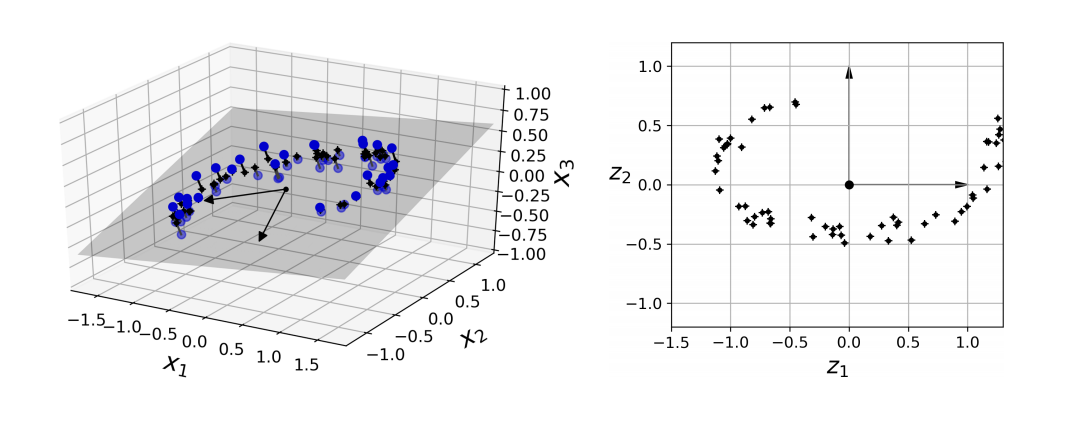
그러나 사영이 항상 최선의 차원 축소 기법은 아니다. 롤케이크형의 데이터를 $x_1, x_2$를 축으로 사영시키면 샘플 구분이 더 복잡해지는 결과가 나타난다.

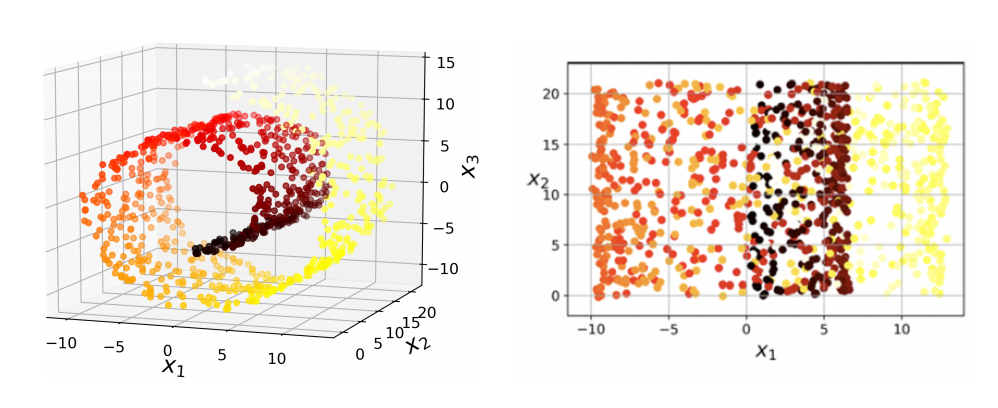
다양체 학습

롤케이크형과 같이 고차원 공간에서 휘어지거나 뒤틀린 저차원 다양체가 있다면 다양체 학습(manifold learning)을 적용하는 것이 더 효과적이다. 다양체 학습은 훈련 샘플이 놓여 있는 다양체를 모델링하여 작동한다.

롤케이크 데이터에 다양체 학습을 적용하여 롤케이크를 펼치면 더 적절한 2차원 데이터가 나온다.

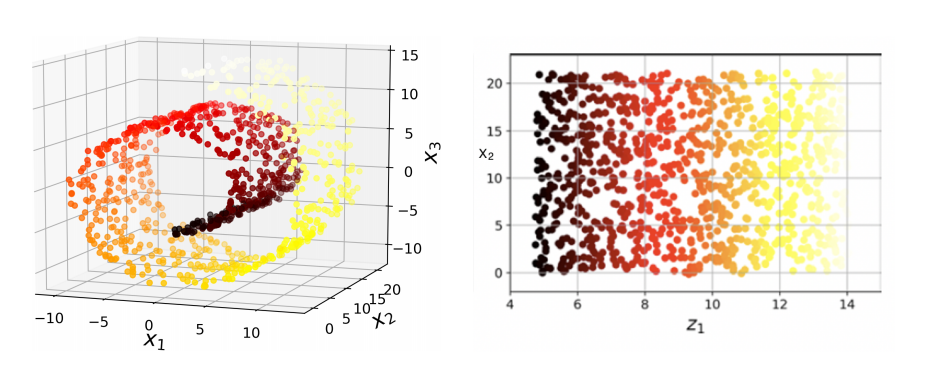
다양체 가정
다양체 학습은 대부분의 고차원 데이터가 저차원 다양체에 가깝다는 다양체 가정에 근거한다.
예를 들어 MNIST 데이터셋에서 숫자 이미지는 나름의 규칙을 가지고 있어서, 무작위 픽셀 이미지에 비해 훨씬 적은 이미지만 존재한다. 숫자 이미지를 만드는 자유도는 무작위 픽셀 이미지의 자유도에 비해 훨씬 낮으므로 고차원 픽셀 데이터를 저차원 다양체로 줄일 수 있다.

다양체 학습은 또한 저차원 다양체로 차원 축소를 하면 다음과 같이 문제가 더 간단해진다는 가정을 함께 사용한다.

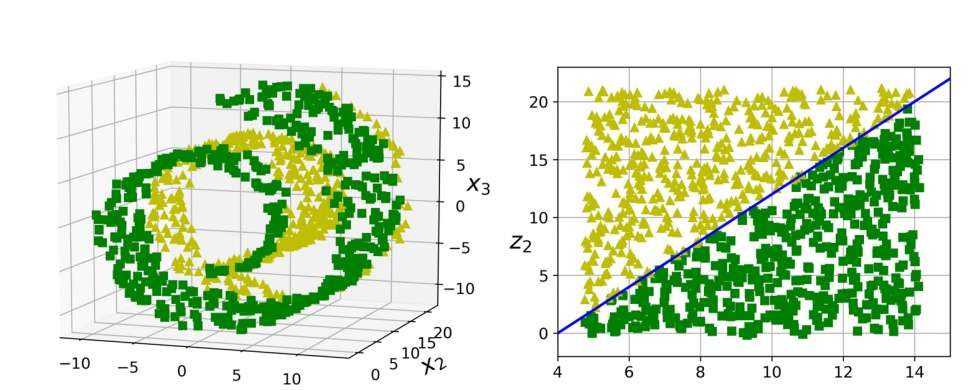
하지만 일반적으로 성립하는 사실은 아니다. 다음 3차원 데이터에서는 $x_1=5$라는 명확한 결정 경계가 있었지만 이를 2차원 다양체로 펼쳤더니 결정 경계가 더 복잡해졌다.

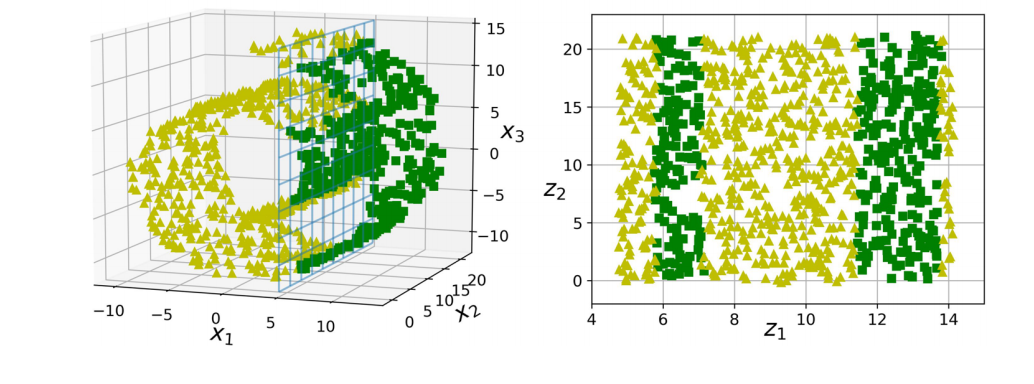
따라서 사영이나 다양체 학습을 사용했을 때 더 나은 솔루션을 줄 수 있을지는 데이터셋에 전적으로 달렸다.

차원 축소 기법을 활용한 학습 알고리즘

• 사영을 사용한 알고리즘 : PCA (주성분분석), 커널 PCA (비선형 사영)
• 다양체 학습을 사용한 알고리즘 : LLE (지역 선형 임베딩)

3. PCA

주성분분석(PCA, principlal component analysis)은 가장 많이 사용되는 차원 축소 알고리즘이다. PCA는 훈련 데이터에 가장 가까운 초평면을 정의한 다음, 그 평면에 사영하는 기법이다. 이때 분산 보존 개념과 주성분 개념이 중요하다.

분산 보존

저차원으로 데이터를 사영할 때 훈련 세트의 분산이 최대한 유지되도록 축을 지정해야 한다는 것이다.

왼쪽 데이터의 경우, $c_1$ 벡터를 축으로 사영해야 분산을 최대한 보존할 수 있다.

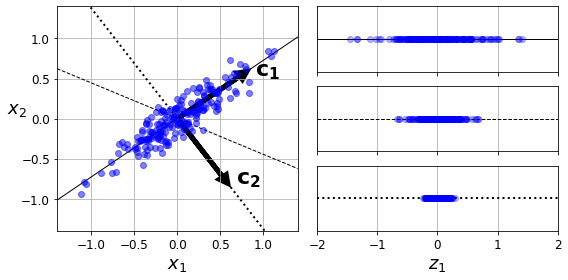
사영시킬 초평면의 축을 선택할 때 분산을 최대한 보존하는 축을 선택하는 것이 정보 손실이 가장 적어서 합리적이다. 이때 원본 데이터셋과 사영된 데이터셋 사이의 평균제곱거리가 최소화된다.

주성분 (PC)

• 첫째 주성분: 분산을 최대한 보존하는 축
• 둘째 주성분: 첫째 주성분과 수직하면서 분산을 최대한 보존하는 축
• 셋째 주성분: 첫째, 둘째 주성분과 수직을 이루면서 분산을 최대한 보존하는 축
  ...

일반적으로 $n$차원 데이터에서 주성분 $n$개를 선택하는 경우 $(n-1)$개의 주성분을 선택하면 마지막 주성분은 자동으로 결정된다.

주성분은 특잇값 분해(SVD)를 이용하여 얻을 수 있다.
훈련 세트 행렬 $X$를 SVD로 분해하면 다음과 같다.

• $V$: 주성분 행렬. ($c_i$ : $i$번째 주성분의 단위 벡터)
  $V= \begin{pmatrix} \vert & \vert & & \vert \\ c_{1} & c_{2} & \ldots & c_{n} \\ \vert & \vert & & \vert \end{pmatrix}$
• $X$: $m \times n$ 행렬, $U$: $m \times m$ 행렬, $\Sigma$ : $m \times n$ 행렬, $V$: $n \times n$ 행렬.
  (훈련 샘플의 개수: $m$, 특성 수: $n$)

❓ 특잇값 분해 뭐드라. 어떻게 주성분 나오는거제. (282 P 15번)

$n$차원 데이터셋을 $d$차원으로 축소하고 싶은 경우 $n$개의 주성분 중 $d$번째 주성분까지를 선택하여 행렬곱으로 데이터셋 $X$를 $d$차원으로 사영하면 된다.

• $X_{d-proj}$ : $d$차원으로 축소된 데이터셋
• $W_d$ : 주성분 행렬 $V$의 첫 $d$열로 구성된 행렬. ($d$번째 주성분까지 포함)

SVD를 이용한 PCA의 구현
3차원 데이터셋의 주성분을 구하고, 이를 적절한 2차원 평면에 사영시켜보자.

앞서 사영을 구현했던 데이터셋을 사용할 것이며, 해당 데이터셋은 다음과 같이 생성되었다.

np.random.seed(4)
m = 60
w1, w2 = 0.1, 0.3
noise = 0.1

angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
X = np.empty((m, 3))
X[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
X[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
X[:, 2] = X[:, 0] * w1 + X[:, 1] * w2 + noise * np.random.randn(m)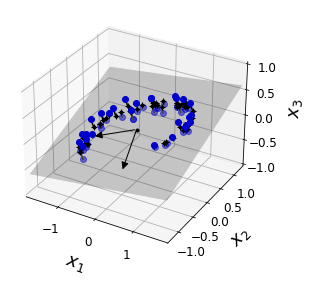

SVD를 사용하여 PC을 구하고, 다음과 같이 처음 두 PC의 단위벡터를 얻었다.

❓ PCA는 왜 평균이 0이어야 하는지는 https://excelsior-cjh.tistory.com/167 요기서 봤었는뎅. 식 전개할 때 필요했던 거 같어.

X_centered = X - X.mean(axis=0)  # PCA는 데이터셋의 평균이 0이라고 가정
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
c1, c2

> (array([0.93636116, 0.29854881, 0.18465208]),
   array([-0.34027485,  0.90119108,  0.2684542 ]))

주성분 행렬의 첫 두 열만 사용하여 행렬곱으로 데이터셋을 사영시켰다.

W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)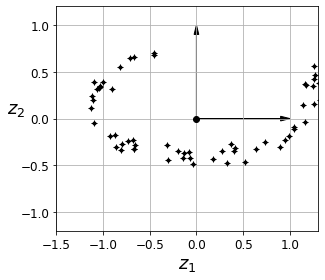

결과적으로 분산을 최대한 유지하며 2차원으로 축소된 데이터셋이 만들어졌다.

Scikit-learn의 PCA

sklearn.decomposition의 PCA로 사이킷런에서 PCA를 사용할 수 있다. 이는 SVD를 사용하며, 자동으로 데이터의 평균을 0으로 맞춰준다.

아래와 같은 코드로 데이터셋 $X$를 2차원으로 차원 축소할 수 있다.

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X2D = pca.fit_transform(X)

PCA를 사용하고 나면 components_에 $d$번째 주성분까지의 행렬 $W_d$의 전치행렬이 담겨 있다.

pca.components_

> array([[-0.93636116, -0.29854881, -0.18465208],
       [ 0.34027485, -0.90119108, -0.2684542 ]])

앞서 직접 구현한 PCA에서 얻은 첫 두 PC와 부호를 제외하고는 동일한 값을 나타내는 것을 볼 수 있다.

설명된 분산의 비율
explained_variance_ration_에는 각 주성분에 대한 원 데이터셋의 분산 비율이 저장된다.

pca.explained_variance_ratio_
> array([0.84248607, 0.14631839])

앞서 사용했던 3차원 데이터셋의 경우, 첫 두 PC로 대부분의 분산이 설명되고, 마지막 주성분은 1.2% 정도만 분산에 기여하여 매우 적은 양의 정보가 포함된 것을 알 수 있다.

적절한 차원 수 선택하는 방법
데이터 시각화가 목적이라면 2차원이나 3차원으로 줄이는 것이 적합하다.

시각화가 목적이 아니라면, 축소할 차원을 선택하는 첫번째 방법은 설명된 분산의 비율의 합이 95% 정도 되도록 하는 주성분들로 구성하는 것이다.
n_components에 0에서 1 사이의 실수를 입력하면 보존하려는 분산의 비율에 맞춰 주성분의 수가 정해진다. 다음과 같은 코드로 분산의 95%를 유지하는 PCA를 적용할 수 있다.

pca = PCA(n_components=0.95)
X2D = pca.fit_transform(X)

이처럼 비율을 설정하는 것이 더 낫지만, 비율이 아닌 주성분의 수를 구하여 지정해줄 수도 있다. 차원을 축소하지 않고 주성분 전체에 대해서 PCA를 계산하고, 설명된 분산의 비율로부터 필요한 최소한의 차원 수를 얻으면 된다. 아래 코드로 얻은 값을 n_components=d로 지정하여 PCA를 실행하면 된다.

pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
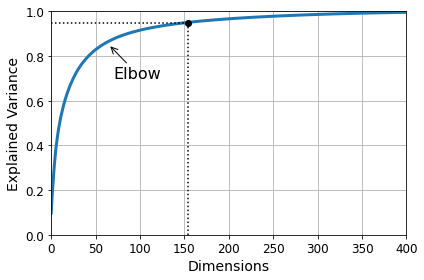
d = np.argmax(cumsum >= 0.95) + 1  #cumsum >= 0.95가 True(1, max)인 것 중 가장 먼저 나오는 index

적절한 차원을 선택하는 두번째 방법은 설명된 분산 비율의 합과 차원 수 사이의 그래프를 그려, 비율의 합이 완만하게 증가하는 지점(elbow)를 선택하는 것이다. cumsum을 그래프로 그려서 다음과 같다면 100차원 정도로 축소해도 분산을 충분히 설명할 수 있다.

PCA를 활용한 MNIST 데이터의 압축과 복원
PCA를 활용하여 MNIST 데이터의 차원을 축소할 수 있다.

MNIST 데이터의 분산을 95% 보존하는 주성분의 개수를 계산해보자.

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
pca.n_components_
> 154

기존에 MNIST는 784개의 픽셀을 차원으로 가졌는데 이 중 154개만 가지고도 분산이 대부분 유지된다. 즉 데이터를 대부분 보존하면서 크기를 원본의 20% 미만으로 줄였다. 이러한 전처리가 진행되면 SVM과 같은 분류 알고리즘의 속도가 크게 빨라질 수 있다.

압축된 데이터셋에 PCA 사영을 반대로 적용하여 원래 차원으로 되돌릴 수 있다. 사영하는 중에 5% 정도의 분산을 이미 잃어서, 원본 데이터셋과 동일한 데이터셋으로 복원되지는 않지만 원본과 매우 비슷한 데이터셋이 얻어질 것이다. 이때 발생하는 원본 데이터와 압축 후 복원한 데이터 사이의 평균제곱거리를 재구성 오차라고 한다.

차원 축소된 데이터셋에 $W_d$의 전치행렬을 곱하면 원본 데이터와 같은 차원으로 복원된다.

• $X_{recovered}$ : 복원된 데이터셋
• $W_d$ : $n$차원을 $d$차원으로 낮춘 행렬 ($W_d^T$는 $d$차원을 $n$차원으로 높여줌)

inverse_transform() 메서드는 PCA 사영된 데이터의 복원을 구현한다. 다음과 같은 코드로 MNIST 데이터셋을 154차원으로 압축한 뒤 다시 784차원으로 복원해보자.

pca = PCA(n_components=154)
X_reduced = pca.fit_transform(X_train)
X_recovered = pca.inverse_transform(X_reduced)

이미지의 품질은 조금 떨어졌지만 숫자를 인식하는데는 전혀 문제를 일으키지 않는 수준이다.

랜덤 PCA
SVD로 주성분을 계산하는 과정에 확률적 알고리즘을 적용하여, 지정된 개수의 주성분에 대한 근삿값을 보다 빠르게 찾는 기법이다. 완전한 SVD로 주성분을 얻는 계산 복잡도는 $O(m \times n^2)+O(n^3)$인데, 랜덤 PCA로 $d$개의 주성분 근삿값을 찾는 계산 복잡도는 $O(m \times d^2)+O(d^3)$이다. 따라서 $d$가 $n$보다 많이 작을 때는 기본 PCA보다 랜덤 PCA가 유용하다.

PCA의 매개변수 svd_solver="randomized"로 지정하면 랜덤 PCA가 수행된다.

rnd_pca = PCA(n_components=154, svd_solver="randomized")
X_reduced = rnd_pca.fit_transform(X_train)

지정해주지 않더라도, $m$이나 $n$이 500보다 크고, d가 m이나 n의 80%보다 작으면 사이킷런은 자동으로 랜덤 PCA를 수행한다. 완전한 SVD를 이용한 기본 PCA를 강제하고 싶으면 svd_solver="full"을 사용할 수 있다.

점진적 PCA
훈련세트를 미니배치로 나눈 후 점진적 PCA(Incremental PCA)에 하나씩 주입하는 기법이다. 이는 SVD를 위해 전체 훈련 세트를 메모리에 올릴 필요가 없으므로 훈련 세트가 매우 클 때 유용하다. 또한 새로운 데이터가 실시간으로 준비되는 온라인 학습에 적용할 수 있다.

Numpy의 array_split() 함수로 훈련세트를 미니배치로 나눌 수 있고, IPCA를 사용할 때는 fit() 대신 partial_fit()을 사용해야 한다.

from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)

X_reduced = inc_pca.transform(X_train)

혹은 Numpy의 memmap() 클래스를 활용하여 이진 파일로 저장된 매우 큰 데이터셋을 마치 메모리에 들어있는 것처럼 취급할 수 있다. 이 클래스는 필요할 때 데이터를 메모리에 적재하고, IPCA는 특정 순간에 데이터의 일부만을 사용하므로 메모리 부족 문제가 해결된다. 이를 이용할 경우 fit()을 사용하면 된다.

4. 커널 PCA

🛑 커널은 어려왕. 담에 할랭. / 여기서 롤케익 데이터 생성 언급 안하면 LLE에서 해롸.

5. LLE

지역 선형 임베딩(Locally Linear Embedding, LLE)는 비선형 차원축소 기법으로, 사영이 아닌 다양체학습에 의존한다.

LLE는 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는지를 측정하고, 이후 국소적 관계가 가장 잘 보존되는 훈련 세트의 저차원 표현을 찾는다. 이는 잡음이 많지 않은 다양체를 펼칠 때 잘 작동한다.


Scikit-learn의 LocallyLinearEmbedding을 사용하여 롤케이크를 펼칠 수 있다.

from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)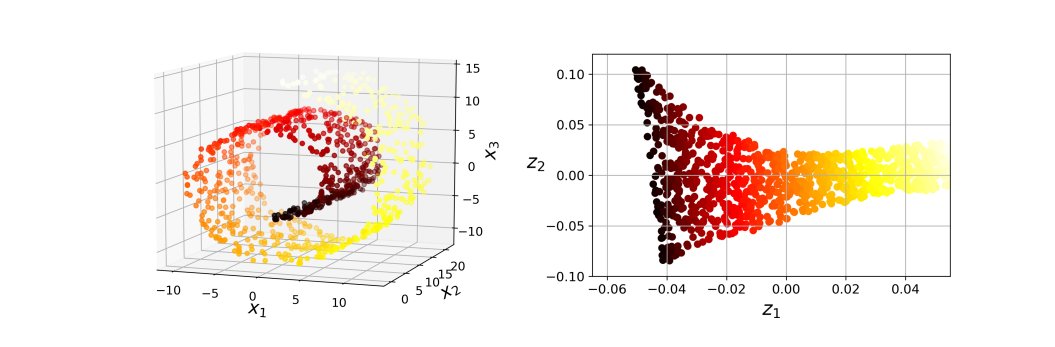

🛑 왕 여기부터도!

Reference
핸즈온 머신러닝 By 오렐리앙 제롱(Aurélien Géron)
이계식 교수님의 슬라이드 http://formal.hknu.ac.kr/handson-ml2/