[프로그래머스/파이썬] (동적계획법(Dynamic Programming)) 정수 삼각형

출처

문제 설명

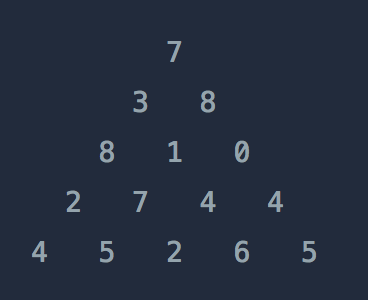
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한사항

• 삼각형의 높이는 1 이상 500 이하입니다.

• 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

입출력 예

triangle	result
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]	30

내 풀이

def solution(triangle):
    for h, tri in enumerate(triangle):
        if h > 0:
            for i in range(h+1):
                if i == 0:
                    tri[i] += triangle[h-1][0]
                elif i == len(tri) - 1:
                    tri[i] += triangle[h-1][-1]
                else:
                    tri[i] += max(triangle[h-1][i-1], triangle[h-1][i])
    return max(triangle[-1])

효율성 테스트: ~47.10ms / 14.7MB

맨 꼭대기부터 맨 밑까지의 높이를 h로 두고, h는 0부터 len(triangle)-1까지이다.
각 지점에서 바로 윗 칸에서 어디서 오는 것이 최적일지를 판단하고 그 때의 합을 누적한다.
h가 len(triangle)-1일 때의 각 요솟값은 그 지점까지 최적의 경로를 따라 왔을 때의 삼각형의 값의 합이다.

예를 들어서
h가 1일 때 0번 인덱스는 7-3 경로가 최적이고 합인 10으로 다시 설정하고 1번 인덱스도 7-8 경로에 대한 15를 입력한다.
변경된 triangle은 다음과 같다.

# h     triangle
# 0        7
# 1      10 15
# 2     8  1  0
# 3    2  7  4  4
# 4   4  5  2  6  5

h가 2일 때는 0번 인덱스는 10으로부터 오고 2번 인덱스는 15로부터 온다.
그리고 1번 인덱스는 10과 15중 15가 크므로 15로부터 온다.
0층을 신경쓰지 않는 이유는 1층이 누적값이기 때문이다.
변경된 triangle은 다음과 같다.

# h     triangle
# 0        7
# 1      10 15
# 2     18 16 15
# 3    2  7  4  4
# 4   4  5  2  6  5

이 과정을 끝까지 거치면

# h     triangle
# 0        7
# 1      10 15
# 2     18 16 15
# 3    20 25 20 19
# 4   24 30 27 26 24

triangle은 위와 같다.

triangle[4]의 최댓값인 30을 출력한다.

다른 풀이

solution = lambda t, l = []: max(l) if not t else solution(t[1:], [max(x,y)+z for x,y,z in zip([0]+l, l+[0], t[0])])

효율성 테스트: ~30.35ms / 20.9MB

가독성을 떠나서 꽤 까다로운 문제인데 한 줄로 표현한 게 너무 놀랍다.

우선은 재귀함수이며 매번 t = t[1:]로 triangle을 한 층씩 낮춘다.
l은 삭제된 t의 각 지점까지 누적해서 더한 최댓값의 리스트이다.
zip([0]+l, l+[0], t[0])을 통해 모서리에 zero padding 해주고 max(x,y), 즉 윗 층의 왼쪽과 오른쪽 중 큰 값을 t[0]의 z에 더해 l을 새로 만든다. 이 l의 길이는 t[0]와 같다.
이 과정을 반복해서 t가 없어진다면 모든 층을 다 누적해서 l에 더했다는 뜻이므로 max(l)을 반환한다.