[자료구조/알고리즘] 코딩 테스트 준비
- 알고리즘
프로그래밍에서는 input 값을 통해 output 값을 얻기 위한 계산 과정을 의미
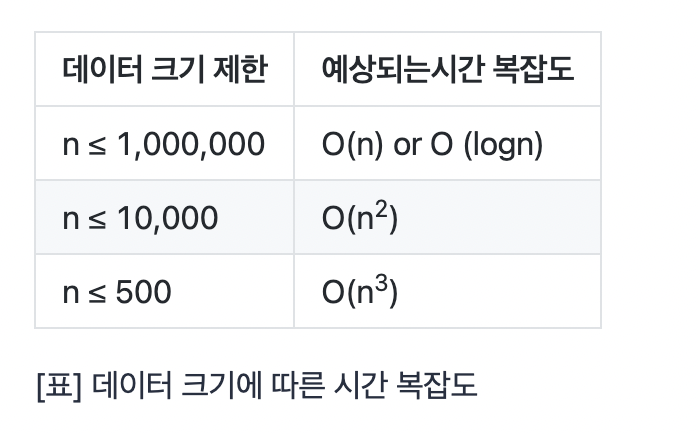
입력-출력-유한성-명확성-효율성
- 시간복잡도
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?
시간 복잡도는 주로 빅-오 표기법을 사용
- Big-0 표기법
프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려한다.
-
O(1)
입력값이 증가하더라도 시간이 늘어나지 않는다.
입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미function O_1_algorithm(arr, index) { return arr[index]; } let arr = [1, 2, 3, 4, 5]; let index = 1; let result = O_1_algorithm(arr, index); console.log(result); // 2 -
O(n)
입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미function O_n_algorithm(n) { for (let i = 0; i < n; i++) { // do something for 1 second } } function another_O_n_algorithm(n) { for (let i = 0; i < 2n; i++) { // do something for 1 second } } -
O(log n)
O(1) 다음으로 빠른 시간 복잡도를 가진다.
up&down 방식의 BST의 값 탐색도 같은 로직의 알고리즘 -
O(n제곱)
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미function O_quadratic_algorithm(n) { for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { // do something for 1 second } } } function another_O_quadratic_algorithm(n) { for (let i = 0; i < n; i++) { for (let j = 0; j < n; j++) { for (let k = 0; k < n; k++) { // do something for 1 second } } } } -
O(2의 n제곱)
Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.function fibonacci(n) { if (n <= 1) { return 1; } return fibonacci(n - 1) + fibonacci(n - 2); }
-
공간 복잡도
알고리즘이 수해되는 데에 필요한 메모리의 총량을 의미
프로그램이 요구하는 공간은 고정적인 공간과 함께 가변적인 공간을 함께 요구
고정적인 공간은 처리할 데이터의 양에 무관하게 항상 요구되는 공간으로서, 프로그램의 성능에 큰 영향을 주지 않는다.
그러나 가변적인 공간은 처리할 데이터의 양에 따라 다르게 요구되는 공간으로서 프로그램의 성능에 큰 영향을 준다.function factorial(n) { if(n === 1) { return n; } return n*factorial(n-1); } 변수 n에 따라 변수 n이 n개가 만들어지게 되며, factorial 함수를 재귀함수로 1까지 호출할 경우 n부터 1까지 스택에 쌓이게 된다. 따라서 해당 함수의 공간 복잡도는 O(n)
- Greedy Algorithm
선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법
문제를 해결하는 과정에서 매 순간, 최적이라 생각되는 해답을 찾으며, 이를 토대로 최종 문제의 해답에 도달하는 문제 해결 방식
- Greedy Algorithm 문제 해결 단계
- 선택 절차: 현재 상태에서의 최적의 해답을 선택합니다.
- 적절성 검사: 선택된 해가 문제의 조건을 만족하는지 검사합니다.
- 해답 검사: 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복합니다.
- 탐욕 알고리즘의 특징
탐욕적 선택 속성 : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
최적 부분 구조 : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
- Algorithm 구현의 기초
-내가 생각한 문제 해결 과정을 컴퓨팅 사고로 변환하여 코드로 구현한다는 것
-본인이 선택한 프로그래밍 언어의 문법을 정확히 알고 있어야 하며, 문제의 조건에 전부 부합하는 코드를 실수 없이 빠르게 작성하는 것을 목표로 두는 것
-완전 탐색이란 가능한 모든 경우의 수를 전부 확인하여 문제를 푸는 방식을 뜻하고, 시뮬레이션은 문제에서 요구하는 복잡한 구현 요구 사항을 하나도 빠트리지 않고 코드로 옮겨, 마치 시뮬레이션을 하는 것과 동일한 모습을 그린다.
- 완전 탐색
문제를 해결할 수 있지만 효율적으로 작동하지는 못한다.
완전히 탐색하는 방법에는 Brute Force(무차별 대입), 재귀, 순열, DFS/BFS 등 여러 가지가 있다. - 시뮬레이션
시뮬레이션은 모든 과정과 조건이 제시되어, 그 과정을 거친 결과가 무엇인지 확인하는 유형
-
Dynamic programming (DP , 동적계획법)
-탐욕 알고리즘(Greedy)과 함께 언급하는 알고리즘
-탐욕 알고리즘과 같이 작은 문제에서 출발한다는 점은 같으나 탐욕 알고리즘이 매 순간 최적의 선택을 찾는 방식이라면 DP는 모든 경우의 수를 조합해 최적의 해법을 찾는다.
-주어진 문제를 여러 개의 (작은) 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결
-하위 문제를 계산한 뒤 그 해결책을 저장
-나중에 동일한 하위 문제를 만날 경우 저장된 해결책을 적용해 계산 횟수를 줄인다.
-하나의 문제는 단 한 번만 풀도록 하는 알고리즘이 바로 이 다이내믹 프로그래밍 -
DP에서 필요한 조건
Overlapping Sub-problems :
큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제가 중복해서 발견된다.
대표적인 예시가 피보나치 수열
작은 문제의 결과를 큰 문제를 해결하기 위해 여러 번 반복하여 사용할 수 있을 때, 부분 문제의 반복이라는 조건을 만족
주어진 문제를 단순히 반복 계산하여 해결하는 것이 아니라, 작은 문제의 결과가 큰 문제를 해결하는 데에 여러 번 사용될 수 있어야 합니다
Optimal Substructure :
작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다.
대표적인 예시가 최단경로찾기
- 예시
-
Greedy Algorithm
function keepTheChange(input) { //1000엔짜리 지폐를 냈다는 가정이 있고, 입력 값으로는 지불해야 할 금액이 들어옵니다. let change = Number(1000 - input); //카운트하기 위해 변수 count에 0을 할당합니다. let count = 0; //입력 값에 배열이 들어오지 않으므로 직접 배열을 만들어줍니다. const joiCoins = [500, 100, 50, 10, 5, 1]; //만든 배열의 개수만큼만 돌려줘야 합니다. for(let i = 0; i < joiCoins.length; i++){ //거스름돈이 0원이 되면 for문을 멈춥니다. if(change === 0) break; //거스름돈과 잔돈을 나눈 몫을 카운팅합니다.(쓰인 잔돈의 개수 카운팅) count += Math.floor(Number(change/joiCoins[i])); //거스름돈을 잔돈으로 나눈 나머지를 재할당합니다. change %= joiCoins[i]; } //count를 리턴합니다. return count; } -
Brute-Force Algorithm
무차별 대입 방법을 나타내는 알고리즘
공간복잡도와 시간복잡도의 요소를 고려하지 않고 최악의 시나리오를 취하더라도 솔루션을 찾으려고 하는 방법순차 검색 알고리즘 function SequentialSearch2(arr, k) { // 검색 키 K를 사용하여 순차 검색을 구현 // 입력: n개의 요소를 갖는 배열 A와 검색 키 K // 출력: K값과 같은 요소 인덱스 또는 요소가 없을 때 -1 let n = arr.length; // 현재의 배열 개수를 n에 할당합니다. arr[n] = k; // 검색 키를 arr n인덱스에 할당합니다. let i = 0; // while 반복문의 초기 값을 지정하고 while (arr[i] !== k) { // 배열의 값이 k와 같지 않을 때까지 반복합니다. i = i + 1; // k와 같지않을 때 i를 +1 합니다. } if (i < n) { // i가 k를 할당하기전의 배열개수보다 적다면(배열안에 k값이 있다면) return i; // i를 반환합니다. } else { return -1; // -1을 반환합니다. } } 문자열 매칭 알고리즘 function BruteForceStringMatch(arr, patternArr) { // Brute Force 문자열 매칭을 구현합니다. // 입력: n개의 문자 텍스트를 나타내는 배열 T, m개의 문자 패턴을 나타내는 배열P // 출력: 일치하는 문자열이 있으면 첫번째 인덱스를 반환합니다. 검색에 실패한 경우 -1을 반환합니다. let n = arr.length; // 13 let m = patternArr.length; //4 for (let i = 0; i <= n - m; i++) { //9 // 전체 요소개수에서 패턴개수를 뺀 만큼만 반복합니다. 그 수가 마지막 비교요소이기 때문입니다. // i 반복문은 패턴과 비교의 위치를 잡는 반복문입니다. let j = 0; // j는 전체와 패턴의 요소 하나하나를 비교하는 반복문입니다. while (j < m && patternArr[j] === arr[i + j]) { // j가 패턴의 개수보다 커지면 안되기때문에 개수만큼만 반복합니다. // 패턴에서는 j인덱스와 전체에서는 i + j 인덱스의 값이 같은지 판단합니다. // 같을때 j에 +1 합니다. j = j + 1; } if (j === m) { // j와 패턴 수가 같다는 것은 패턴의 문자열과 완전히 같은 부분이 존재한다는 의미입니다. // 이 때의 비교했던 위치를 반환합니다. return i; } } return -1; } 선택 정렬 알고리즘 function SelectionSort(arr) { // 주어진 배열을 Selection Sort로 오름차순 정렬합니다. // 입력: 정렬 가능한 요소의 배열 A // 출력: 오름차순으로 정렬된 배열 for (let i = 0; i < arr.length - 1; i++) { // 배열의 0번째 인덱스부터 마지막인덱스까지 반복합니다. // 현재 값 위치에 가장 작은 값을 넣을 것입니다. let min = i; // 현재 인덱스를 최소값의 인덱스를 나타내는 변수에 할당합니다. for (let j = i + 1; j < arr.length; j++) { // 현재 i에 +1을 j로 반복문을 초기화하고 i 이후의 배열요소과 비교하는 반복문을 구성합니다. if (arr[j] < arr[min]) { // j인덱스의 배열 값이 현재 인덱스의 배열 값보다 작다면 min = j; // j 인덱스를 최소를 나타내는 인덱스로 할당합니다. } } // 반복문이 끝났을 때(모든 비교가 끝났을때) // min에는 최소값의 인덱스가 들어있습니다. // i값과 최소값을 바꿔서 할당합니다. let temp = arr[i]; arr[i] = arr[min]; arr[min] = temp; } // 모든 반복문이 끝나면 정렬된 배열을 반환합니다. return arr; } -
Dynamic Programming - 피보나치 수열과 타일링
DP를 이용하여 피보나치 수열 문제를 해결하려고 할 때, 크게 두 가지 방식 Recursion + Memoization 과 Iteration + Tabulation 이 있다.Recursion + Memoization function fibMemo(n, memo = []) { // 이미 해결한 하위 문제인지 찾아본다 if(memo[n] !== undefined) { return memo[n]; } if(n <= 2) { return 1; } // 없다면 재귀로 결괏값을 도출하여 res 에 할당 let res = fibMemo(n-1, memo) + fibMemo(n-2, memo); // 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장 memo[n] = res; return res; } Iteration + Tabulation function fibTab(n) { if(n <= 2) { return 1; } // n 이 1 & 2일 때의 값을 미리 배열에 저장해 놓는다 let fibNum = [0, 1, 1]; for(let i = 3; i <= n; i++) { fibNum[i] = fibNum[i-1] + fibNum[i-2]; // n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여 // n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다 } return fibNum[n]; }
2X1타일링
function tiling2x1(n) {
let memo = [0, 1, 2];
for (let i = 3; i <= n; i++) {
memo[i] = memo[i - 1] + memo[i - 2];
}
return memo[n];
};
순열과 조합
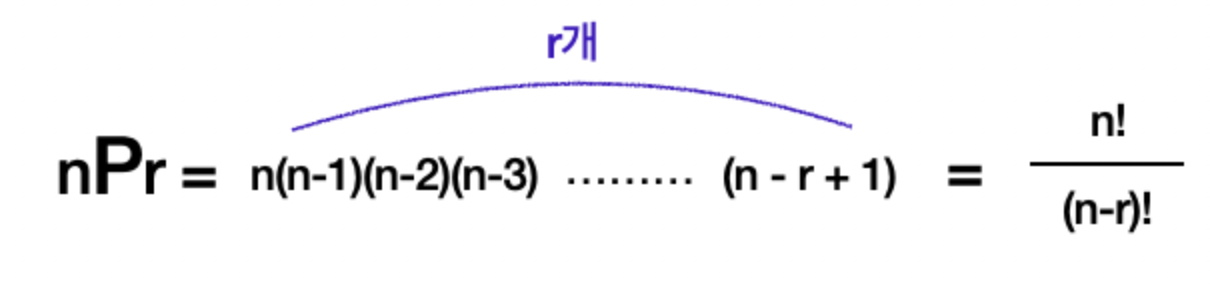
n= 원소의 총 개수 , r= 뽑는 개수

최대공약수 최소공배수
-
유클리드 호제법 : 두 수의 최대공약수를 구하는 알고리즘
MOD연산이란? 두 값을 나눈 나머지를 구하는 연산
유클리드 호제법은 MOD연산을 반복하면 된다. -
최소공배수
두 수 a와 b의 최소공배수는 a와 b의 곱을 a와 b의 최대공약수를 나눈 것
멱집합
- 어떤 집합이 있을 때 이 집합의 모든 부분집합을 멱집합이라고 한다.
원소가 있는지, 없는지 2가지 경우를 고려하기 때문에 집합의 요소가 n개일 때 모든 부분집합의 개수는 2의 n개이다. tip. 약수구하려면 제곱근을 이용해!
정규 표현식
문자열에서 특정한 규칙에 따른 문자열 집합을 표현하기 위해 사용되는 형식 언어
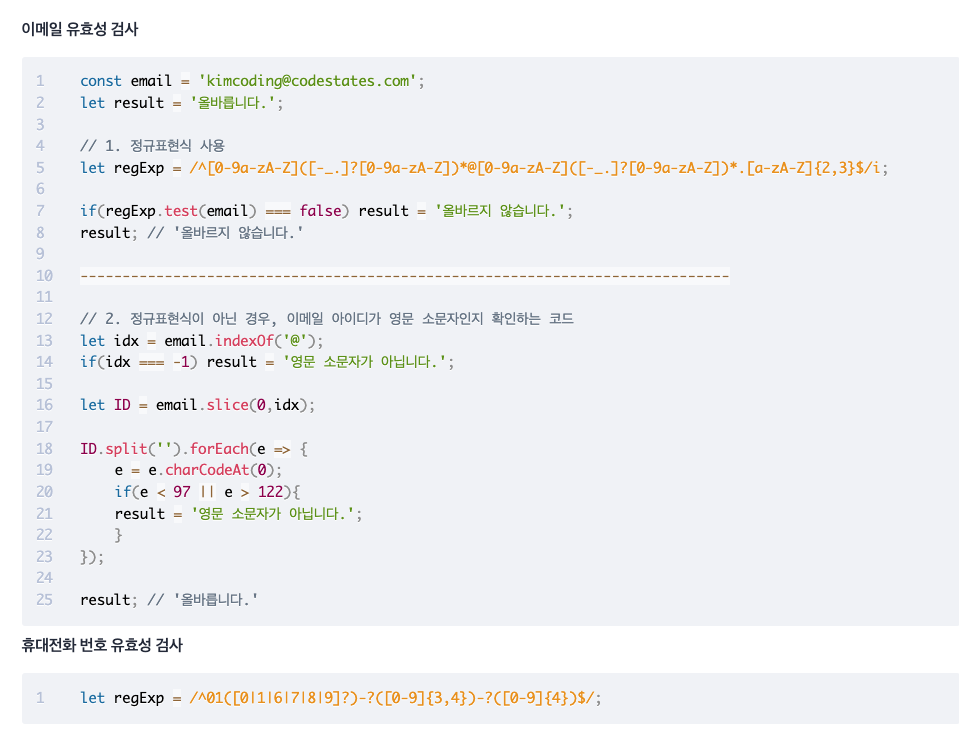
정규표현식 사용하기
-
리터럴 패턴
정규표현식 규칙을 슬래시(/)로 감싸 사용
let pattern = /c/; -
생성자 함수 호출 패턴
RegExp 객체의 생성자 함수를 호출하여 사용한다.

