2.1 퍼셉트론이란?

2.2 단순한 논리회로
2.2.1 AND 게이트

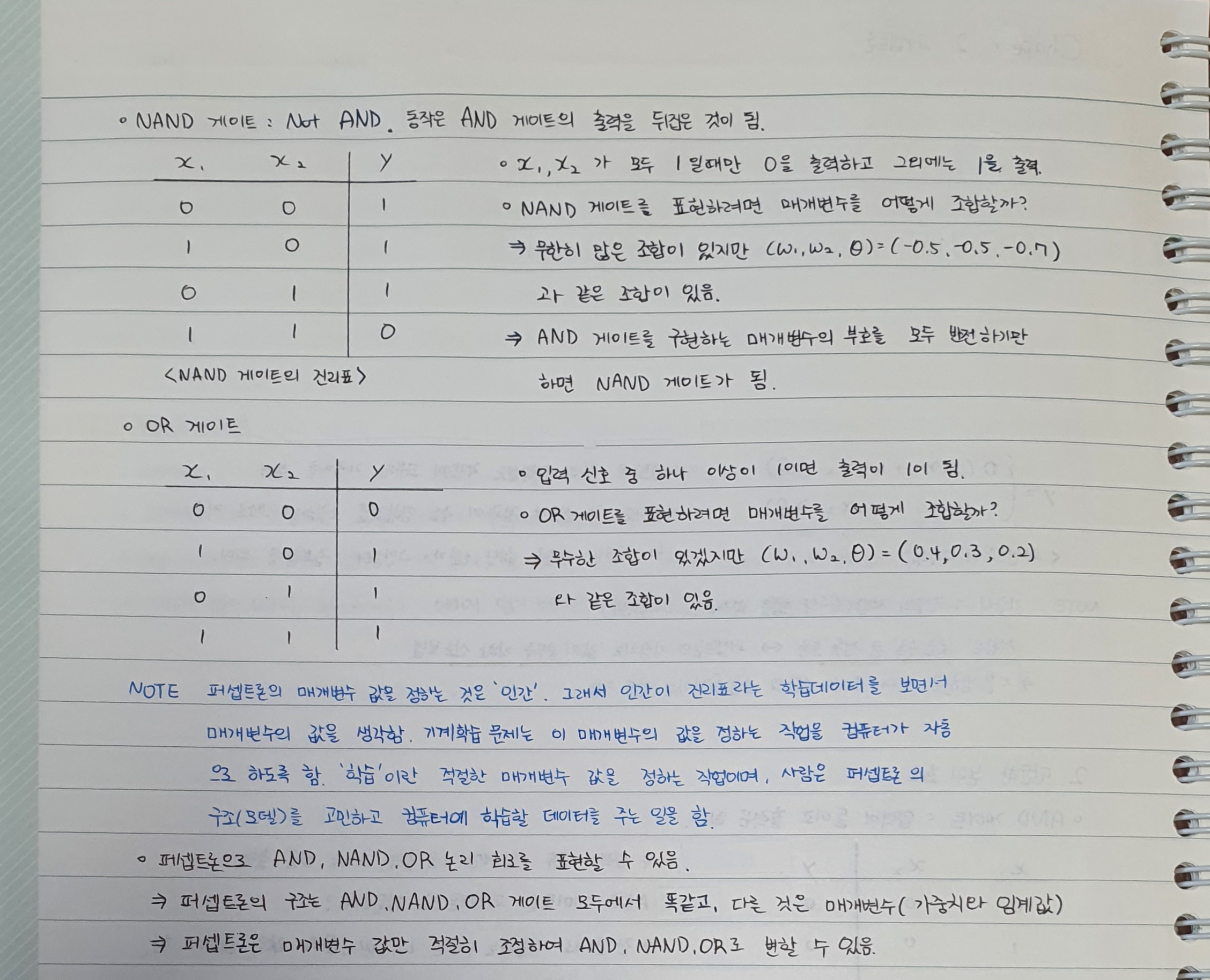
2.2.2 NAND 게이트와 OR 게이트
2.3 퍼셉트론 구현하기
2.3.1 간단한 구현부터
x1과 x2를 인수로 받는 AND 함수
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1+ x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
- 매개변수 w1, w2, 는 함수 안에서 초기화 하고, 가중치를 곱한 입력의 총합이 임계값을 넘으면 1을 반환하고 그외에는 0을 반환.
출력결과
AND(0, 0) # 0이 출력
AND(1, 0) # 0이 출력
AND(0, 1) # 0이 출력
AND(1, 1) # 1이 출력2.3.2 가중치와 편향 도입
- 위의 식에서 는 -b로 치환하면 퍼셉트론의 동작이 아래와 같이 바뀜.
퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력한다.
- 단, 위 식과 아래 식은 기호 표기만 바꿨을 뿐 그 의미는 같음.
- 여기서 b를 편향(bias)라고 하며 w1과 w2는 그대로 가중치임.
넘파이로 아래 식 구현해보기
import numpy as np
x = np.array([0, 1]) # 입력
w = np.array([0.5, 0.5]) # 가중치
b = -0.7 # 편향
w*x결과: array([0. , 0.5])- 넘파이 배열끼리 곱셈은 두 배열의 원소 수가 같다면 각 원소끼리 곱함.
- 그래서 w*x에서는 인덱스가 같은 원소끼리 곱함.
np.sum(w*x)결과: 0.5- np.sum()메서드는 입력한 배열에 담긴 모든 원소의 총합을 계산함.
np.sum(w*x)+b결과: -1.9999999999999996 # 약 -0.2- 이 가중치에 편향을 더하면 계산 완료!
2.3.3 가중치와 편향 구현하기
가중치와 편향을 도입한 AND 게이트
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1-
여기에서 가 편향 b로 치환됨.(2.3.1에서 구현한 theta가 -b가 됨.)
-
편향은 가중치 w1, w2와 기능이 다르다는 사실에 주의.
-
가중치 w1, w2는 각 입력 신호가 결과에 주는 영행력(중요도)를 조절하는 매개변수이지만,
편향은 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수인 셈. -
편향의 값은 뉴런이 얼마나 쉽게 활성화되는지를 결정.
b = -0.1이면 각 입력 신호에 가중치를 곱한 값들의 합이 0.1을 초과할 때만 뉴런 활성화 O
b = -20.0이면 각 입력 신호에 가중치를 곱한 값들의 합이 20.0을 넘지않으면 뉴런 활성화 X -
책에서 문맥에 따라 w1, w2, b를 가중치라고 할때도 있음.
노트
- 편향: 한쪽으로 치우쳐 균형을 깬다.
- 실제로 아래 식에서 두 입력이 모두 0이어도 결과로 (0이 아닌) 편향 값을 출력.
NAND 게이트
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # AND와는 가중치(w, b)만 다르다.
b = 0.7
tmp = sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1OR 게이트
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와는 가중치(w, b)만 다르다.
b = -0.2
tmp = sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1- AND, NAND, OR는 모두 같은 구조의 퍼셉트론이고, 차이는 가중치 매개변수의 값 뿐이라 코드에서도 해당 부분만 다름.
2.4 퍼셉트론의 한계
2.4.1 도전! XOR 게이트
- XOR 게이트는 '배타적 논리합'이라는 논리 회로.(배타적 = 자기 외에는 거부)
- x1과 x2 중 한쪽이 1일 때만 1을 출력.
- XOR 게이트는 지금까지 본 퍼셉트론으로 구현 X.
왜 AND,OR은 되고 XOR 게이트는 안되나?
- OR 게이트의 동작은, 예를들어, 가중치 매개변수가 (b , w1, w2) = (-0.5, 1.0, 1.0)일 때 진리표를 만족함.
- 퍼셉트론 식으로는 다음과 같음.
-
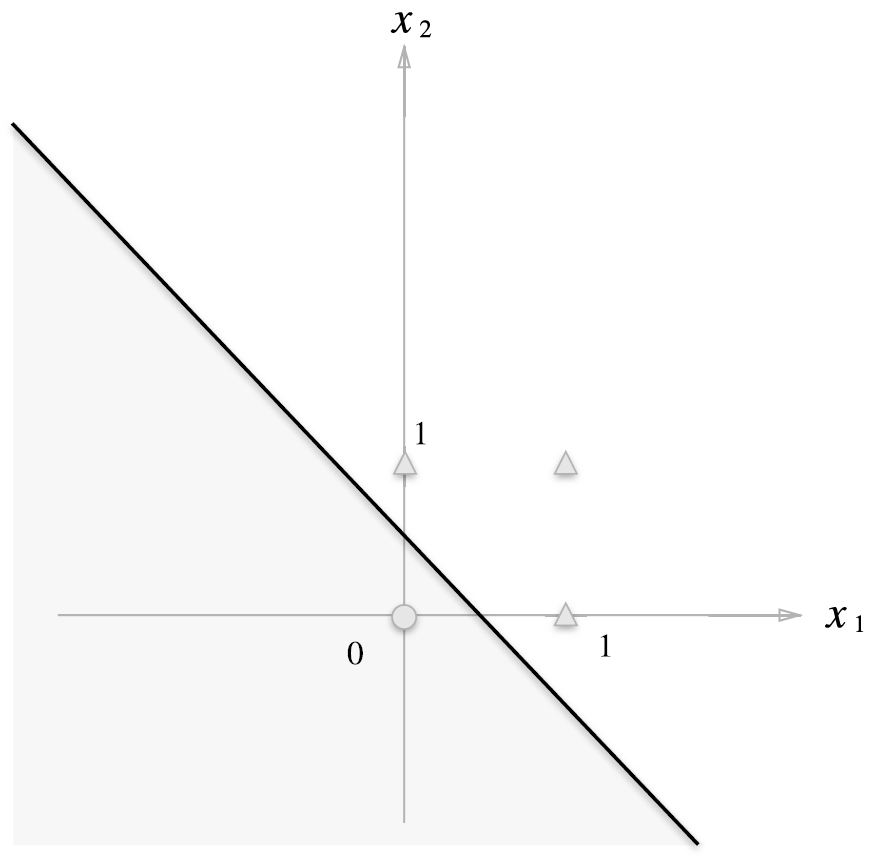
해당 페셉트론은 직선으로 나뉜 두 영역을 생성. 직선으로 나뉜 한쪽 영역은 1을 출력하고 다른 한쪽은 0을 출력함.
-
퍼셉트론의 시각화: 회색영역은 0을 출력하는 영역, 전체 영역은 OR 게이트의 성질을 만족
-
OR 게이트는 (x1, x2) = (0, 0)일 때, 0을 출력, (0,1), (1,0), (1,1)일 때, 1을 출력
-
위 그래프에서 0은 원, 1은 삼각형으로 표시. OR 게이트를 만들려면 원과 삼각형을 직선으로 나눠야 하는데 그래프의 직선은 네 점을 잘 나누고 있음.
-
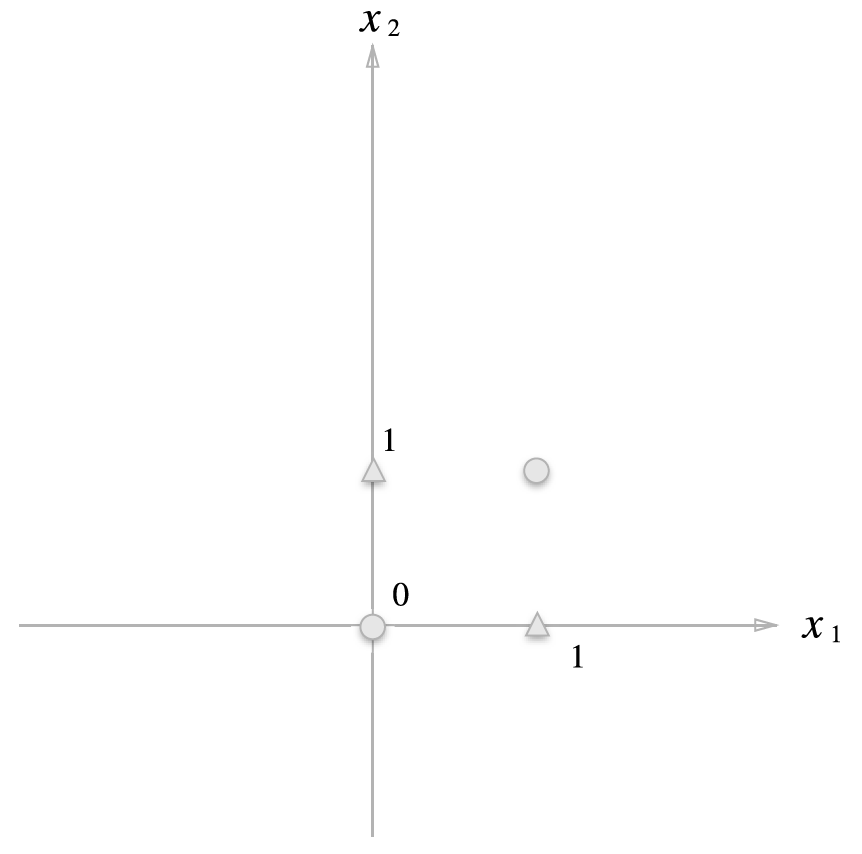
XOR 게이트. 원과 삼각형은 XOR 게이트의 출력을 나타냄.
-
하나의 직선으로 나누기란 불가능.
2.4.2 선형과 비선형
- XOR 게이트는 직선으로 원과 삼각형을 나눌 수 없었지만, 직선이라는 제약을 없앤다면 나눌 수 있게 됨.
(= 곡선은 가능)
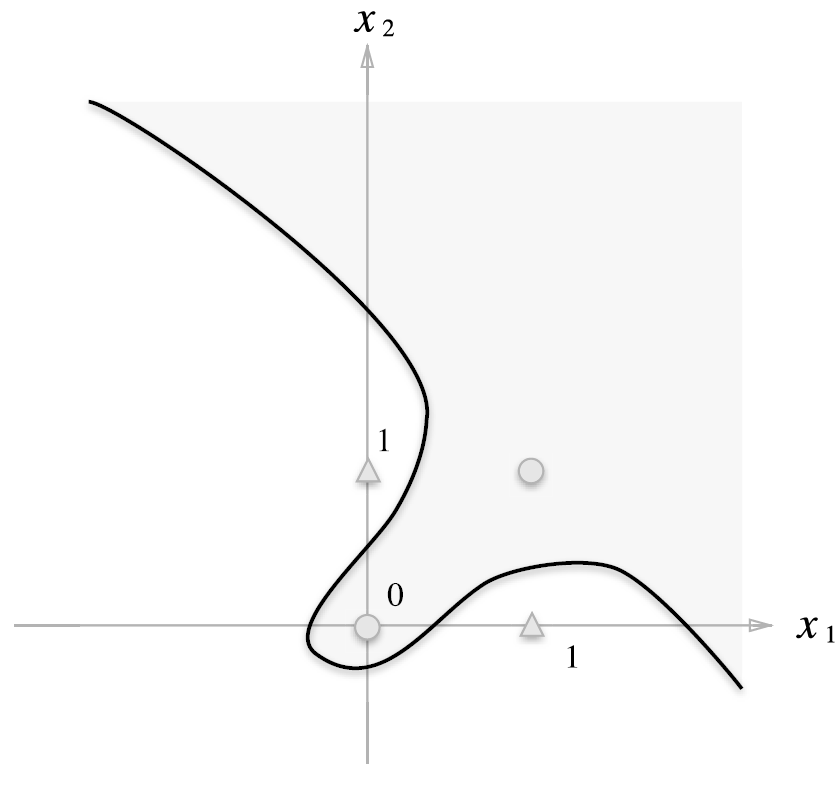
- 퍼셉트론은 직선 하나로만 나눈 영역만 표현할 수 있다는 한계가 존재 = 곡선은 표현.
- 위 그래프와 같은 곡선의 영역을 비선형 영역, 직선의 영역을 선형 영역이라고 함.
2.5 다층 퍼셉트론이 충돌한다면?!
- 퍼셉트론으로 XOR 게이트를 표현할 수는 없지만, 다층퍼셉트론으로는 만들 수 있음.
- 다층 퍼셉트론은 층을 쌓아 만드는 퍼셉트론.
2.5.1 기존 게이트 조합하기
- XOR 게이트를 만드는 방법은 다양하나 앞서봤던 AND, NAND, OR 게이트를 조합하는 방법이 그 중 한 가지.
- 여기서는 AND, NAND, OR 게이트를 각 기호로 표기함. NAND 뒤에 o 기호는 출력을 반전한다는 뜻.

노트
단층 퍼셉트론으로는 비선형 영역을 분리할 수 없기에 퍼셉트론 게이트를 조합하여, 즉 층을 쌓아서 XOR 게이트를 구현하게 될 것임.
- AND, NAND, OR 게이트를 조합하여 XOR 게이트를 구현할 수 있음.
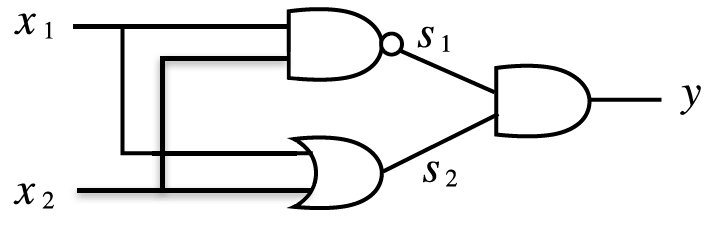
- x1, x2가 입력 신호이고, y가 출력신호. x1, x2는 NAND와 OR 게이트의 입력이 되고, NAND와 OR의 출력이 AND 게이트의 입력으로 이어짐.
- 위 조합이 정말 XOR를 구현하는지 보기 위해 XOR 진리표를 보면 다음과 같음.

- NAND의 출력: s1, OR의 출력: s2
- x1, x2, y를 살펴보면 XOR의 출력과 같음을 알 수 있음.
2.5.2 XOR 게이트 구현하기
XOR 게이트를 파이썬으로 구현
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y출력결과
XOR(0, 0) # 0을 출력
XOR(1, 0) # 1을 출력
XOR(0, 1) # 1을 출력
XOR(1, 1) # 0을 출력- 방금 구현한 XOR을 뉴런을 이용한 퍼셉트론으로 그리면 다음과 같음.
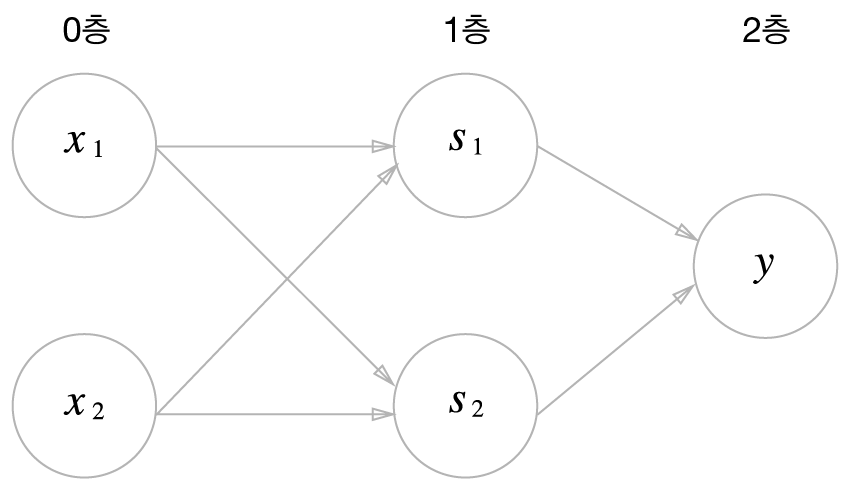
- XOR은 다층 구조의 네트워크.
- AND, OR은 단층 퍼셉트론인데, XOR은 2층 퍼셉트론.
- 이처럼 층이 여러 개인 셉트론을 다층 퍼셉트론이라고 지칭.
노트
위 그림의 퍼셉트론은 모두 3층으로 구성됨. 가중치를 갖는 층은 사실 2개(0층과 1층 사이, 1층과 2층 사이)뿐이라서 우리는 '2층 퍼셉트론'이라고 부르기로 함. 문헌에 따라 3층 퍼셉트론이라고 하기도 함.
-
위 2층 퍼셉트론의 동작은 다음과 같음.
- 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호를 보낸다.
- 1층의 뉴런이 2층의 뉴런으로 신호를 보내고, 2층의 뉴런은 y를 출력한다.
-
2층 구조를 사용해 퍼셉트론으로 XOR 게이트를 구현. = 단층 퍼셉트론으로 표현하지 못한 것을 층을 하나 늘려 구현.
2.6 NAND에서 컴퓨터까지
- 다층 퍼셉트론은 지금까지 보아온 회로보다 복잡한 회로를 만들기 가능
= 컴퓨터도 만들 수 있다?! - 컴퓨터에 무언가를 입력하면 정해진 방법으로 처리하고 그 결과를 출력.
= 퍼셉트론처럼 입/출력으로 구성된 특정한 규칙대로 계산을 수행. - NAND 게이트 조합만으로 컴퓨터가 수행하는 일 재현 가능.
노트
"NAND 게이트 조합만으로 컴퓨터를 만든다"라는 말이 궁금한 분은 'the elements of computer systems building a modern computer from first principles'를 참고.
- 어떤 구조의 퍼셉트론이면 컴퓨터를 표현할 수 있을까? 층을 얼마나 깊게 하면 컴퓨터가 만들어질까?
= 이론상 2층 퍼셉트론이면 컴퓨터를 만들 수 있다. - 비선형인 시그모이드 함수를 활성화 함수로 이용하면 임의의 함수를 표현 가능함이 증명됨.
- 하지만 2층 퍼셉트롬 구조에서 가중치를 적절히 설정해 컴퓨터를 만들기는 어려움.
정리
이번장에서 배운 내용
- 퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- 퍼셉트론에서는 가중치와 편향을 매개변수로 설정한다.
- 퍼셉트론으로 AND, OR 게이트 등의 논리 회로를 표현할 수 있다.
- XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
- 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.
- 단층 퍼셉트온은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.
- 다층 퍼셉트론은 이론상 컴퓨터를 표현할 수 있다.
출처
- 밑바닥부터 시작하는 딥러닝, 사이토 고키, 한빛 미디어
- 이미지:https://github.com/WegraLee/deep-learning-from-scratch.git
