처음에는 깜지쓰듯이 썼는데 그러니깐 너무 시간이 많이 드는군요. 그래서 오늘부터는 공부법을 바꾸어 책에서 눈에 밟히는 부분만 적겠습니다. 공부법을 바꾸기 전에 적은 부분은 그냥 남겨두겠습니다. 그래서 초반엔 장황한데 끝에는 미미할 수 있다는 점 주의바랍니다!

---

3.4.3 구현 정리

• 신경망 구현의 관례: 가중치만 W1처럼 대문자로 쓰고, 편향과 중간결과 등은 소문자로 표기.

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['B1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['B2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['B3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['B1'], network['B2'], network['B3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)    
>>> [0.31682708 0.69627909]

• init_network(): 가중치, 편향을 초기화하고 딕셔너리 변수인 network에 저장.
• 변수 network에는 각 층에 필요한 매개변수(가중치, 편향)을 저장.
• forword(): 입력 신호를 축력으로 변환하는 처리 과정을 모두 구현함. (신호가 순방향으로 전달=순전파)

3.5 출력층 설계하기

• 신경망은 분류, 회귀 모두에 이용 가능.
• 다만 어떤 문제냐에 따라 출력층에서 사용하는 활성화 함수가 달라짐.
• 일반적으로 회귀에는 항등 함수, 분류에는 소프트맥스 함수 사용.

---

노트
분류: 데이터가 어느 클래스에 속하나? (Ex. 사진 속 인물 성별 분류)
회귀: 입력 데이터에서 수치를 예측. (Ex. 사진 속 인물 몸무게 예측)

---

3.5.1 함등 함수와 소프트맥스 함구 구현하기

• 항등 함수: 입력을 그대로 출력.

• 항등 함수에 의한 변환은 은닉층에서의 활성화 함수와 같이 화살표로 그림.
  

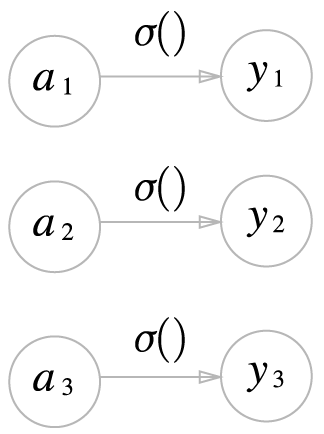
• 한편, 소프트맥스의 식은 다음과 같음.

$y_k=\frac{exp(a_k)}{\sum_{i=1}^nexp(a_i)}$

• exp(x): $e^x$을 뜻하는 지수함수.(e는 자연상수)

• n: 출력층의 뉴런 수,

• $y_k$: 그중 k번째 출력임을 나타냄.

• 소프트맥스 함수의 분자 = 입력 신호 $a_k$의 지수 함수.

• 소프트맥스 함수의 분모 = 모든 입력 신호의 지수 함수의 합.

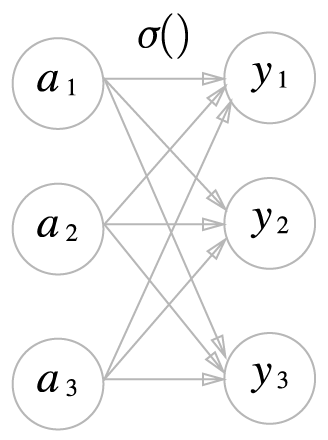
• 소프트맥스의 출력은 모든 입력 신로로부터 화살표를 받음.

• 분모에서 알 수 있듯이 출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문.
  

소프트맥스 함수 구현하기

a = np.array([0.3, 2.9, 4.0])

exp_a = np.exp(a) # 지수 함수
print(exp_a)
>>> [1.34985881 18.17414537 54.59815003]

sum_exp_a = np.sum(exp_a) # 지수 함수의 합
print(sum_exp_a)
>>> 74.1221542102

y = exp_a / sum_exp_a
print(y)
>>> [0.01821127 0.24519181 0.73659691]

• 위는 소프트맥스의 흐름에 따라 구현한 것이고, 아래는 논리 흐름의 정의하여 구현한 것.

def softmax(a): 
	exp_a = np.exp(a) 
    sum_exp_a = np.sum(exp_a) 
    return exp_a / sum_exp_a
    
    return y

3.5.2 소프트맥스 함수 구현 시 주의점

• 컴퓨터로 소프트맥스 함수를 계산할 때는 오버플로 문제가 생김.

• 오버플로 문제란 표현할 수 있는 수보다 큰 수가 올 경우 컴퓨터에서 표현이 불가능하다는 것.

• 소프트맥스 함수는 지수 함수를 사용하는 함. 그래서 결과값이 아주 클 때가 있는데, 이렇게 큰 값끼리 나눗셈을 하면 결과 수치가 불안정해짐.

• 소프트맥스의 이런 문제를 개선한 함수는 다음과 같음.
  

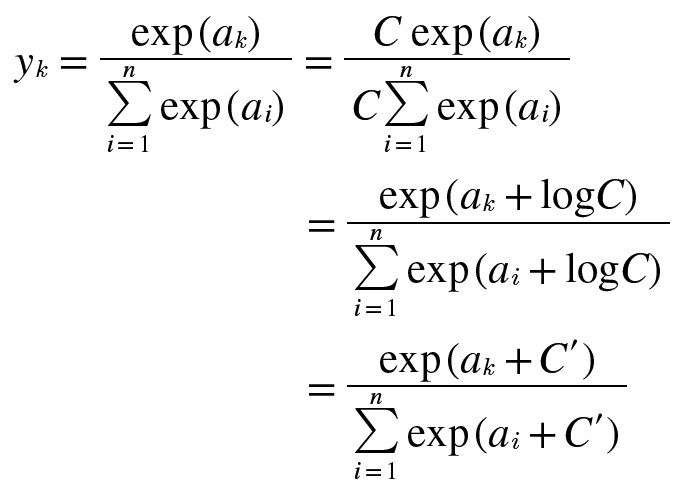
  1. C라는 임의의 정수를 분자와 분모 양쪽에 곱함.
  2. C를 지수 함수 exp() 안으로 옮겨 logC를 생성.
  3. 마지막으로 logC를 $C^{\prime}$라는 새로운 기호로 바꿈.

• 소프트맥스의 지수 함수를 계산할 때 어떤 정수를 더하고 빼도 결과는 바뀌지 않음을 말하고 있음.

• 여기에서 $C^{\prime}$에 어떤 값을 대입해도 상관 없지만 오버플로를 막을 목적으로는 입력 신호 중 최댓값을 이용하는 것이 일반적임.

a = np.array([1010, 1000, 990]) 
np.exp(a) / np.sum(np.exp(a)) # 소프트맥스 함수의 계산 
>>> array([nan, nan, nan]) # 결과값이 제대로 계산X

c = np.max(a) # c=1010(최댓값) 
a - c
>>> array([0, -10, -20])

np.exp(a-c) / np.sum(np.exp(a-c) 
>>> [9.99954600e-01 4.53978686e-05 2.06106005e-09]

• 위 예와같이 아무 조치 없이 계산하면 nan(not a number)이 출력됨.
• 하지만 입력 신호 중 최댓값을 빼주면 올바르게 계산할 수 있음.
• 이를 바탕으로 다시 구현하면 다음과 같음.

def softmax(a): 
	c = np.max(a) 
    exp_a = np.exp(a-c) # 오버플로 해결 
    sum_exp_a = np.sum(exp_a) 
    y = exp_a / sum_exp_a
    return y

3.5.3 소프트맥스 함수의 특징

• 소프트맥스 함수를 사용하면 신경망 출력은 다음과 같이 계산 가능.

a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)    
>>> [0.01821127 0.24519181 0.73659691]
num.sum(y)
>>> 0.1

• 보이는 바와 같이 소프트맥스 함수의 출력은 0 ~ 1 사이의 실수.

• 소프트맥스 함수의 총합은 1. 그래서 소프트맥스 함수의 출력을 확률로 해석 가능.

• 앞 예시에서처럼 y[0]의 확률이 0.018(1.8%), y[1]의 확률은 0.245(24.5%), y[2]의 확률은 0.737(73.7%)로 해석이 가능.

• 이는 "2번째 원소의 확률이 가장 높음. = 답은 2번째 클래스."라고 할 수 있는 것임. 또는 "74%의 확률로 2번째 클래스, 25%의 확률로 1번째 클래스, 1%의 확률로 0번째 클래스"라는 확률적 결론을 낼 수 있음.

• 소프트맥스 함수를 이용하면 확률적으로 대응이 가능해짐.

• 주의점: 소프트먁스 함수를 적용해도 각 원소의 대소 관계는 변하지 않음.

• 왜냐하면 지수 함수 y = exp(x)가 단조 증가 함수이기 때문.

• 신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식.

• 소프트맥수 함수를 적용해도 출력이 가장 큰 뉴런의 위치는 달라지지 않음.

• 그래서 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 빼줘도 됨.

---

노트

• 기계학습의 문제풀이는 학습과 추론으로 이루어짐.
• 학습단계에서는 모델을 학습하고, 추론 단계에서는 앞서 학습한 모델로 미지의 데이터에 대해서 추론(분류)을 수행함.
• 추론 단계에서는 출력층의 소프트맥스 함수를 생략하지만, 신경망 학습 중에는 출력층에서 소프트맥스 함수를 사용함.
• 학습은 좋은 성능을 위해 파라미터를 찾아가는 과정. 역전파를 이용해 최적의 가중치와 편향을 계속 찾아감.(forward, backward)
• 추론은 네트워크 조정 후 학습된 모델이 입력에 따라 예측하는 과정.(forward)

---

3.5.4 출력층의 뉴런 수 정하기

• 출력층의 뉴런 수는 풀려는 문제에 맞게 적정히 설정해야 함.

• 분류에서는 분류하고 싶은 클래스 수로 설정하는 것이 일반적.(Ex. 숫자 0~9 분류 = 10개)
  

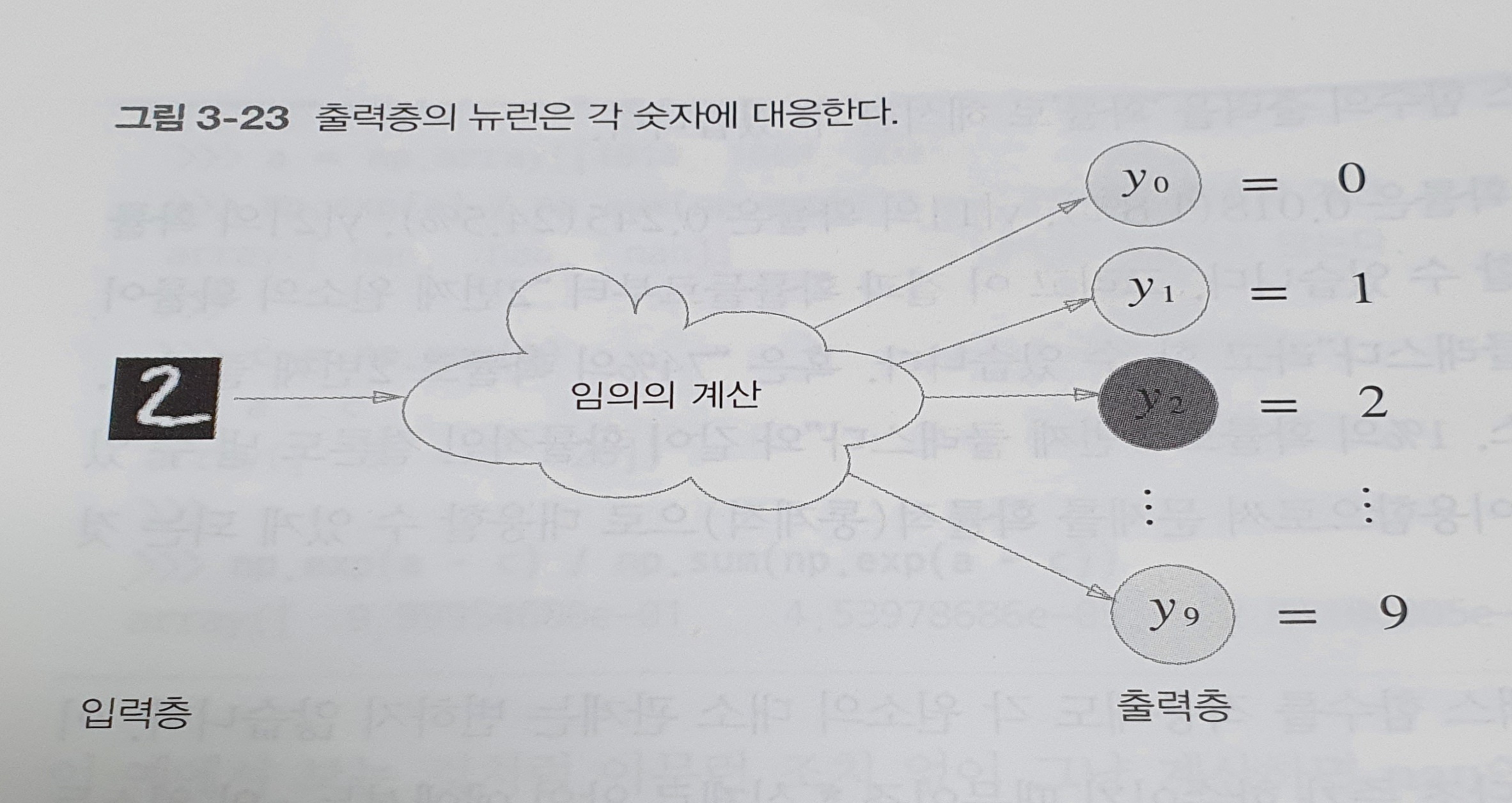
• 위 예에서 출력층의 뉴런은 위에서부터 차례로 숫자 0, 1, ..., 9에 대응하며, 뉴런의 회색 농도가 해당 뉴런의 출력 값의 크기를 의미함.

• 따라서 색이 가장 짙은 $y_2$ 뉴런이 가장 큰 값을 출력하는 것.

• 이 신경망이 선택한 클래스는 $y_2$, 즉 입력 이미지를 숫자 2로 판단했음을 의미.

3.6 손글씨 인식

• 추론과정을 신경망의 순전파 라고도 함.

---

노트

• 신경망도 훈련 데이터를 사용해 가중치 매개변수를 학습하고, 추론 단계에서 앞서 학습한 매개변수를 사용하여 입력 데이터를 분류함.

---

3.6.1 MNIST 데이터셋

• MNIST는 손글씨 숫자의 이미지 집합. 0 ~ 9까지의 숫자 이미지로 구성됨.

• 훈련 이미지: 60,000장, 시험 이미지 10,000장으로 구성.
  

• MNIST의 이미지 데이터는 28x28 크기의 회색조 이미지(1채널)이고, 각 픽셀은 0 ~ 225까지의 값을 취함.

• 각 이미지에는 실제 의미하는 숫자가 레이블로 붙어있음.

---

이 밑부터는 직접 구현해보는 부분입니다. 사실 한빛미디어 깃헙 사이트에서 자료까지 다 받아놨는데 파일 참조가 안되서 막혔습니다. 주말쯤에 다시 해보려고요. 그래서 여기서 사용한 함수 위주로 설명하겠습니다.

---

• load_mnist(): MNIST 데이터를 (훈련 이미지, 훈련 레이블), (시험 이미지, 시험 레이블) 형식으로 반환. 인수로는 normalize, flatten, ont_hot_label을 설정할 수 있음. 모두 bool 값임.

  normalize: 입력 이미지 픽셀 값을 0.0 ~ 1.0 사이로 정규화. False하면 원래 값대로 0 ~ 255 사이의 값을 가짐.
  flatten: 입력 이미지를 1차원 배열로 반환. False하면 원래 차원인 3차원 배열을 반환.
  ont_hot_label: 정답을 뜻하는 원소만 1이고 나머지는 0인 배열을 반환. False하면 원래 숫자를 그대로 반환.

• reshape(): 원하는 형상을 인수로 지정하면 넘파이 배열의 형상을 바꿀 수 있음.

• PIL.Image.fromarray(obj, mode): 이미지를 PIL용 데이터 객체로 변환.

3.6.2 신경망의 추론 처리

• 이 신경망의 입력층 뉴런은 784개, 출력층 뉴런은 10개.

• 입력층 뉴런이 784개인 이유는 이미지 크기가 28*28이기 때문임.

• 출력층의 뉴런이 10개인 이유는 숫자 0 ~ 9까지 구분하는 문제이기 때문.

• 분류의 경우, 출력층의 뉴런 개수는 클래스의 수와 같게 함.

• 뉴런 출력층을 정하는 기준은 데이터 표현의 문제와 직결. 그래서 출력하고자하는 형식에 따라 활성화 함수와 뉴런이 정해짐.

• 이 신경망은 모델 학습 후 추론 결과를 정확도를 기준으로 평가함.

• 데이터를 특벙 범위로 변환하는 처리과정을 정규화(normalization)이라고 하는데 학습을 빠르게 한다는 이점을 가지고 있음. 여기서는 전처리에 해당.

• 전처리는 현업에서도 많이 쓰임. 대신 예시와 같이 단순하진 않고 데이터 전체의 분포를 고려햐 전처리 하는 겨우가 많음.

• 예를 들면 데이터 정체 평균과 표준편차를 이용하여 데이터들이 0을 중심으로 분포하도록 이동하거나 데이터 확산 범위를 제한하는 정규화를 수행. 전체 데이터를 균일하게 분포시키는 데이터 백색화도 있음.

3.6.3 배치처리

• 위 그림은 이미지 데이터를 1장만 입력했을 때 흐름.
  
• 위 그림은 이미지 여러 장을 한번에 입력했을 때 흐름.
• 연산이 많을 경우 하나씩 계산하는 것보다 한무더기로 계산하는 것이 더 좋음.

• 이 한무더기를 여기서는 배치라고 함. 일종의 묶음임.
• 배치 처리는 이미지 1장당 처리 시간을 대폭 줄여줌.
• 이유 1번: 수치 계산 라이브러리가 대부분 큰 배열을 효과적으로 처리할 수 있게 최적화되어있기 때문.
• 이유 2번: 큰 신경망에서는 데이터 전송이 병목으로 작용하는 경우가 있는데 배치처리가 버스에 주는 부하를 줄여줌. 정확히 말하면 느린 I/Od를 통해 데이터를 읽는 횟수가 줄어 빠른 CPU나 GPU가 순수 계산을 하는 비율이 높아짐.

• 하지만 배치사이즈가 커지면 메모리를 많이 잡아먹음.
• 그래서 배치사이즈와 메모리는 트레이드 오프 관계.

• epoch(에포크)는 대이터 전체를 한번 훓어보는 것을 말하며, 배치는 이 에포크 속 덩어리를 말함.

정리

• 이 장의 신경망은 각 층의 뉴런들이 다음 층의 뉴런으로 신호를 전달한다는 점에서 퍼셉트론과 같음.
• 하지만 다음 뉴런으로 이동할 때 신호를 변화시키는 활성화 함수에 차이가 있음.
• 신경망에서는 활성화 함수로 매끄러운 시그모이드, ReLU를 사용, 퍼셉트론에서는 갑자기 변화하는 계단 함수를 사용.
• 넘파이의 다차원 배열을 잘 사용하면 신경망을 효율적으로 구현 가능(행렬의 곱, 특히 브로드캐스트)
• 기계학습 문제는 크게 회귀와 분류로 나뉨. 하지만 머신러닝은 지도학습, 비지도학습, 반지도학습, 강화학습이 있으며 회귀와 분류는 지도학습에 속하는 것임. 클러스터링과 같은 비지도학습에 속하는 기계 학습 문제도 있음.
• 출력층의 활성화 함수로는 회귀에서는 주로 항등함수를, 분류에서는 주로 소프트맥스 함수를 사용.
• 분류에서는 출력층의 뉴런 수를 분류하려는 클래스 수와 같게 설정함.
• 입력 데이터를 묶은 걸 배치라고 하며, 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있음.

출처

• 밑바닥부터 시작하는 딥러닝, 사이토 고키, 한빛 미디어
• 이미지:https://github.com/WegraLee/deep-learning-from-scratch.git