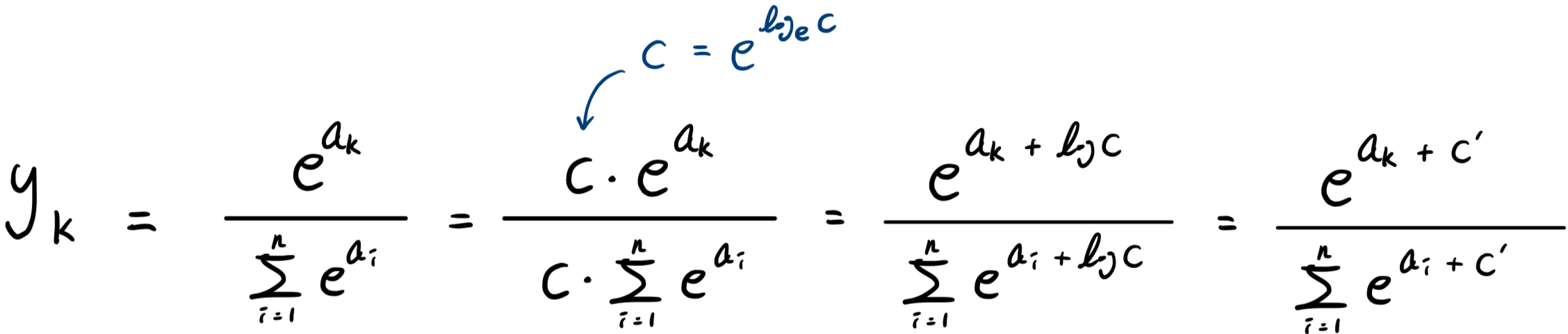[밑바닥부터 시작하는 딥러닝1] 교재 3장을 기반으로 작성되었습니다.
퍼셉트론으로 복잡한 처리까지 할 수 있었지만, 가중치를 적절하게 사람이 설정해주어야하는 불편함이 있었다. 이 불편함을 신경망이 해결해줄 수 있다.
신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하는 능력이 있다!
3.1 퍼셉트론에서 신경망으로
신경망의 예
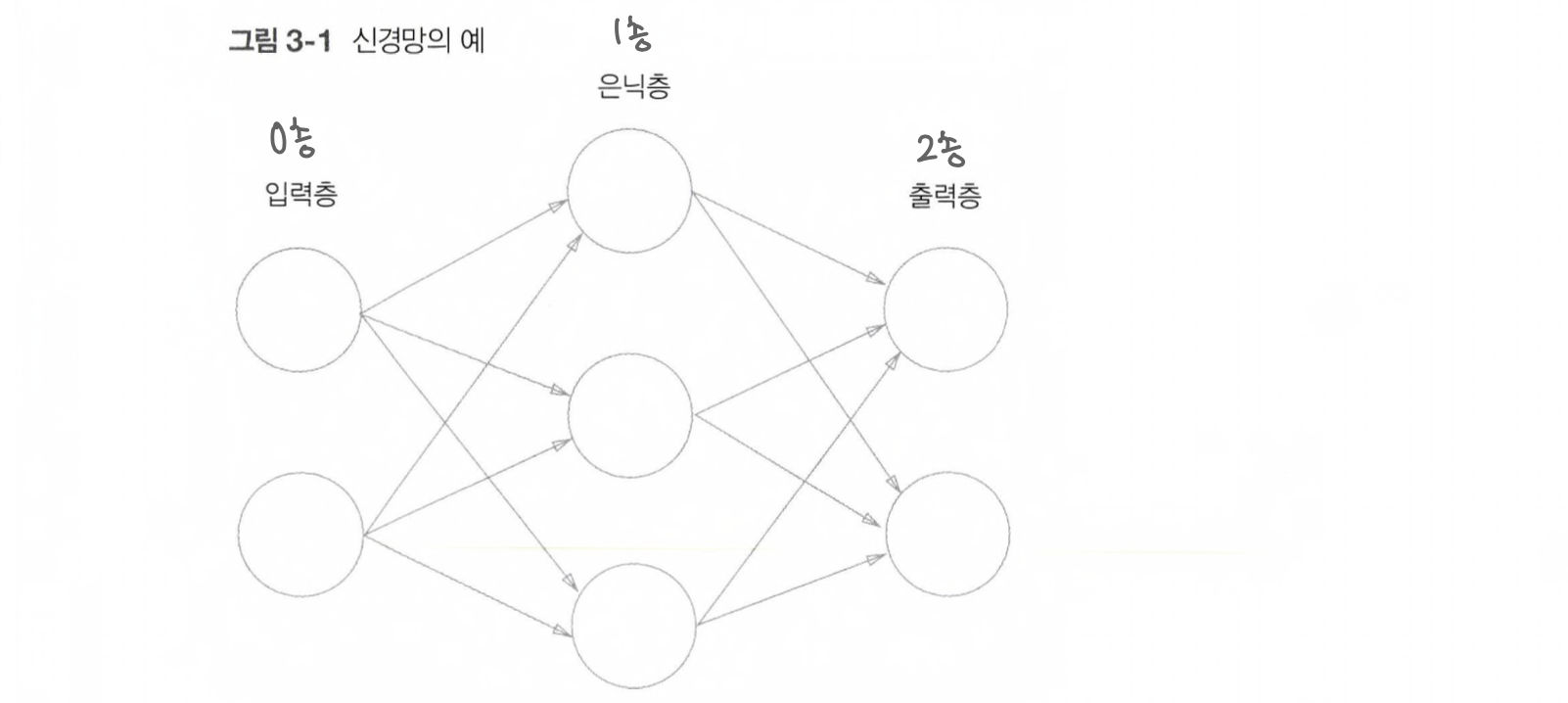
은닉층은 입력층이나 출력층과 달리 말 그대로 사람 눈에 보이지 않기 때문에 붙여진 이름이다.
이전에 본 퍼셉트론과 특별히 달라 보이지 않는다. 이번 장에선 이 둘의 차이점을 알아볼 것이다.
퍼셉트론 복습
차이점을 알아보기 위해 퍼셉트론을 복습해보자.
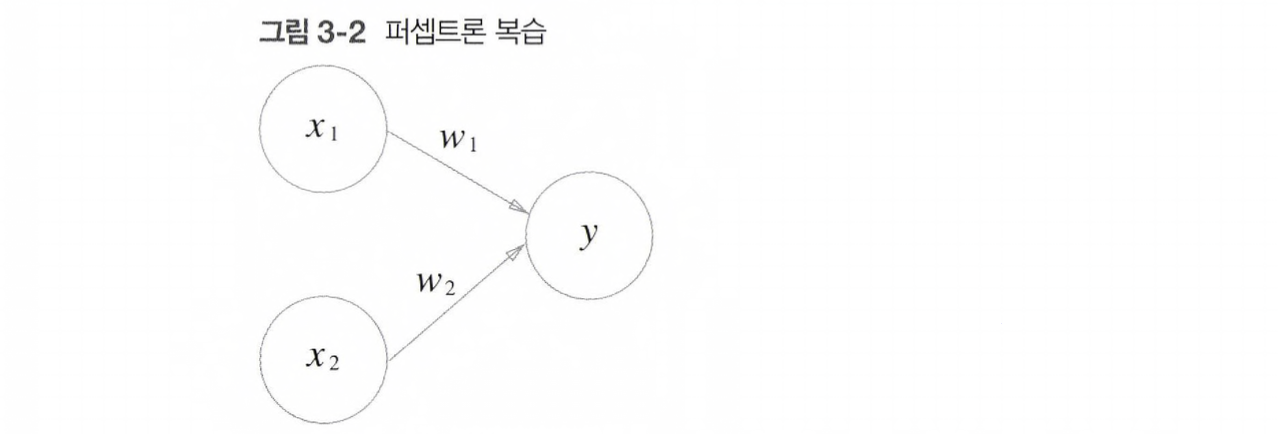
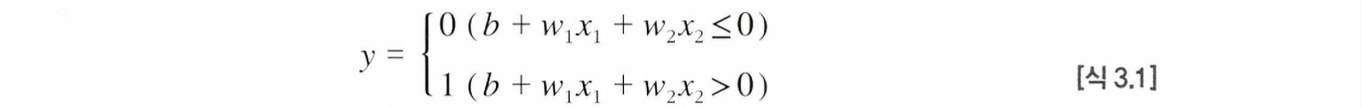
두 신호를 입력받는 퍼셉트론은 위와 같이 나타내어진다. (b=편향, w1,w2=가중치)
하지만 [식 3.1]과 달리 [그림 3-2]에서는 편향 b가 보이지 않는데, 편향 b를 명시하면 아래와 같다.
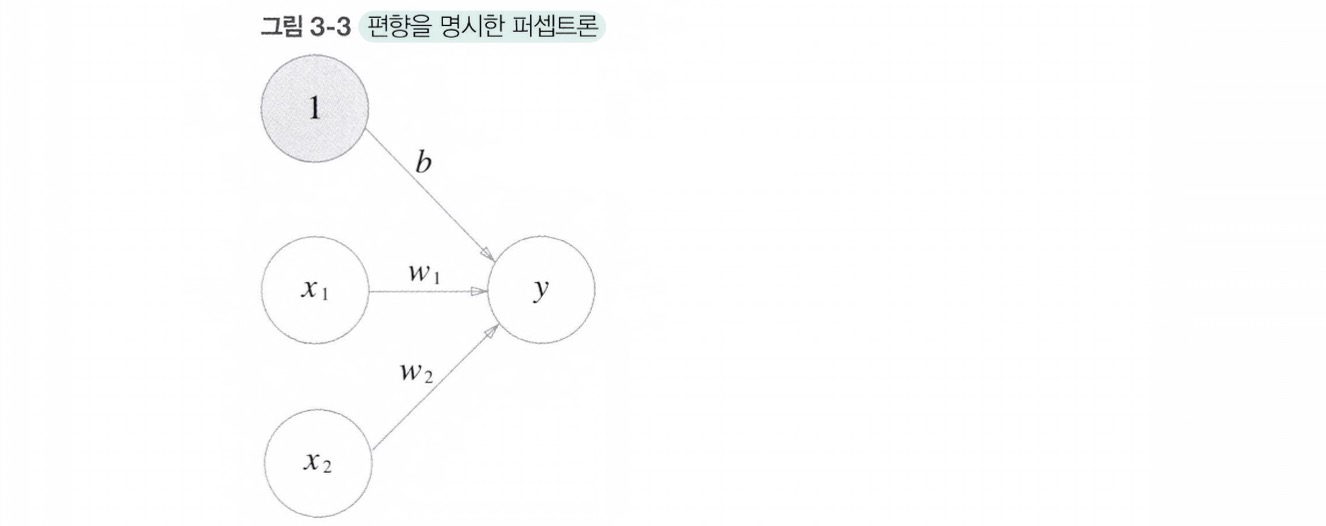
이에 더해, [식3.1]을 더 간결한 형태로 나타내면 아래와 같다.
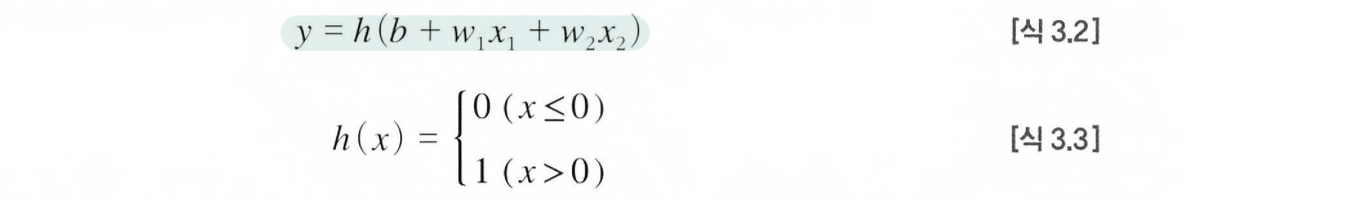
여기서 신호의 총합이 0을 넘으면 1을 출력하고, 그렇지 않으면 0을 출력하는 함수를 h(x)로 나타내주었다. (중요)
활성화 함수의 등장
위의 h(x), 입력 신호의 총합을 출력 신호로 변환하는 함수를 활성화 함수라고 한다.
이 함수는 입력 신호의 총합이 '활성화'를 일으키는지 정하는 역할을 한다.
활성화 함수의 처리 과정을 나타내면 아래와 같다.
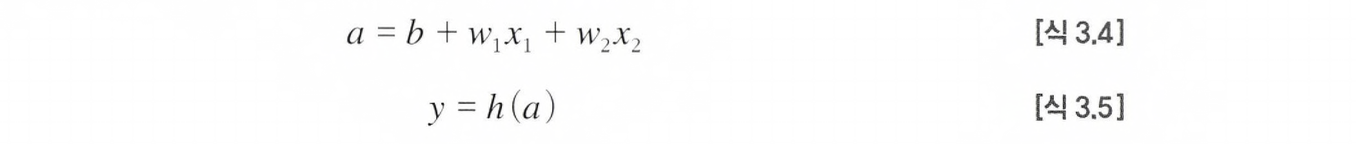
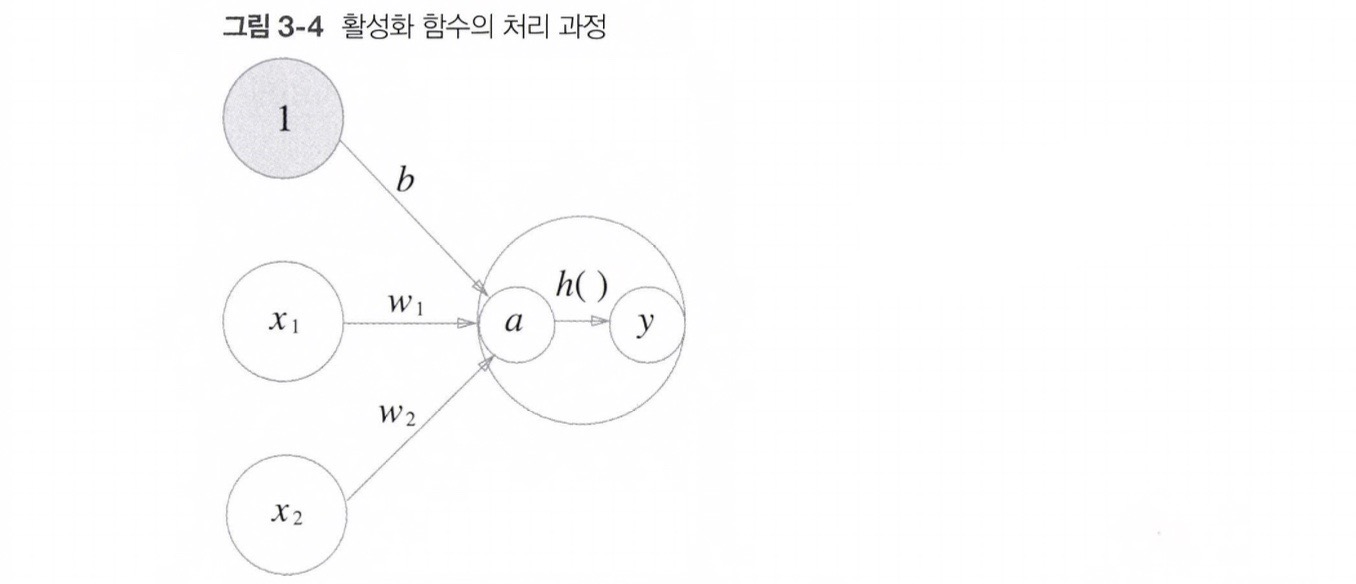
3.2 활성화 함수
퍼셉트론은 계단 함수를 활성화 함수로 사용하고,
신경망은 시그모이드와 같은 매끈한 활성화 함수를 사용한다.
+) 퍼셉트론과 신경망의 가장 큰 차이는 '활성화 함수의 차이'이다!!!
시그모이드 함수
신경망에서 자주 이용하는 활성화 함수인 시그모이드 함수를 식으로 나타내면 아래와 같다.
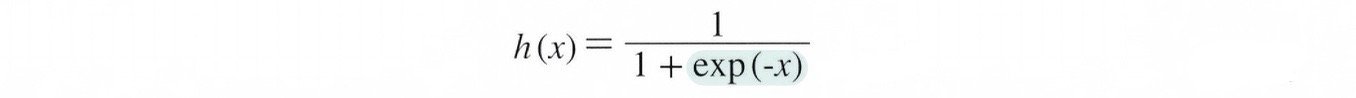
시그모이드 함수의 구현과 그래프는 아래에서 알아보자.계단 함수 구현하기
퍼셉트론에서 사용되는 활성화 함수인 계단 함수를 코드로 구현해보자.
def step_function(x):
if x > 0:
return 1
else:
return 0위의 구현은 직관적이고 간단하지만, 인수 x가 실수만 받을 수 있고 넘파이 배열을 인수로 받을 수 없다.
def step_function(x):
y = x > 0
return y.astype(np.int)위와 같이 구현하면 넘파이 배열도 잘 지원된다. 구동원리를 아래를 통해 이해해보자.
import numpy as np
x = np.array([-1.0, 1.0, 2.0])
x
# >>> array([-1., 1., 2.])
y = x > 0
y
# >>> array([False, True, True])
y = y.astype(int) # 위의 bool 타입을 int 타입으로 타입변환 🚨 교재의 np.int는 더이상 안 쓰인다.🚨
y
# >>> array([0, 1, 1])이제 계단 함수의 그래프를 그려보자.
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x>0, dtype=int) # 🚨 교재의 np.int는 더이상 안 쓰인다.🚨
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y축의 범위 지정
plt.show()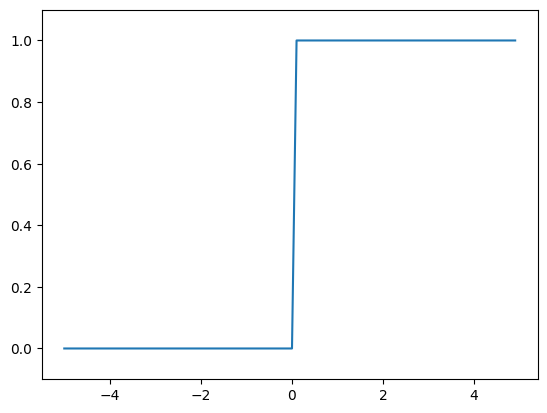
계단 함수는 0을 경계로 출력이 0에서 1로 바뀐다. 이름처럼 '계단'처럼 생긴 것을 확인할 수 있다.
시그모이드 함수 구현하기
이제 시그모이드 함수를 구현해보자.
def sigmoid(x):
return 1 / (1 + np.exp(-x))위 코드는 넘파이 배열도 제대로 처리해주는데, 브로드캐스팅 기능 덕분이다. 아래를 통해 확인/복습해보자.
"""넘파이 배열 처리 확인"""
x = np.array([-1.0, 1.0, 2.0])
sigmoid(x)
# >>> array([0.26894142, 0.73105858, 0.88079708])
"""브로드 캐스팅 복습"""
t = np.array([1.0, 2.0, 3.0])
1.0 + t
# >>> array([2., 3., 4.])
1.0 / t
# >>> array([1. , 0.5 , 0.33333333])
"""
[브로드 캐스트]
넘파이 배열과 스칼라값의 연산을 넘파이 배열의 원소 각각과 스칼라값의 연산으로 바꿔 수행해준다.
"""이제 시그모이드 함수의 그래프를 그려보자.
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y축 범위 지정
plt.show()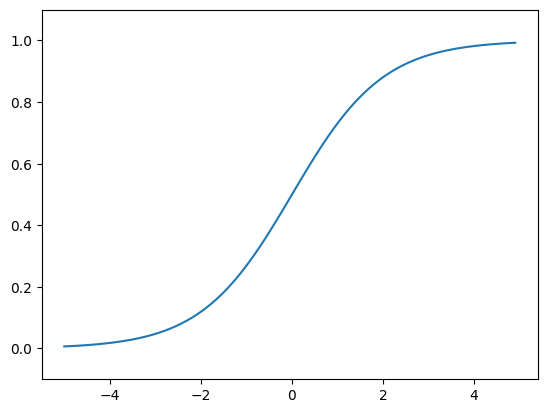
시그모이드(sigmoid)란 'S자 모양'이라는 뜻이다. 계단 함수처럼 그 모양을 따 이름을 지은 것이다.
시그모이드 함수와 계단 함수 비교
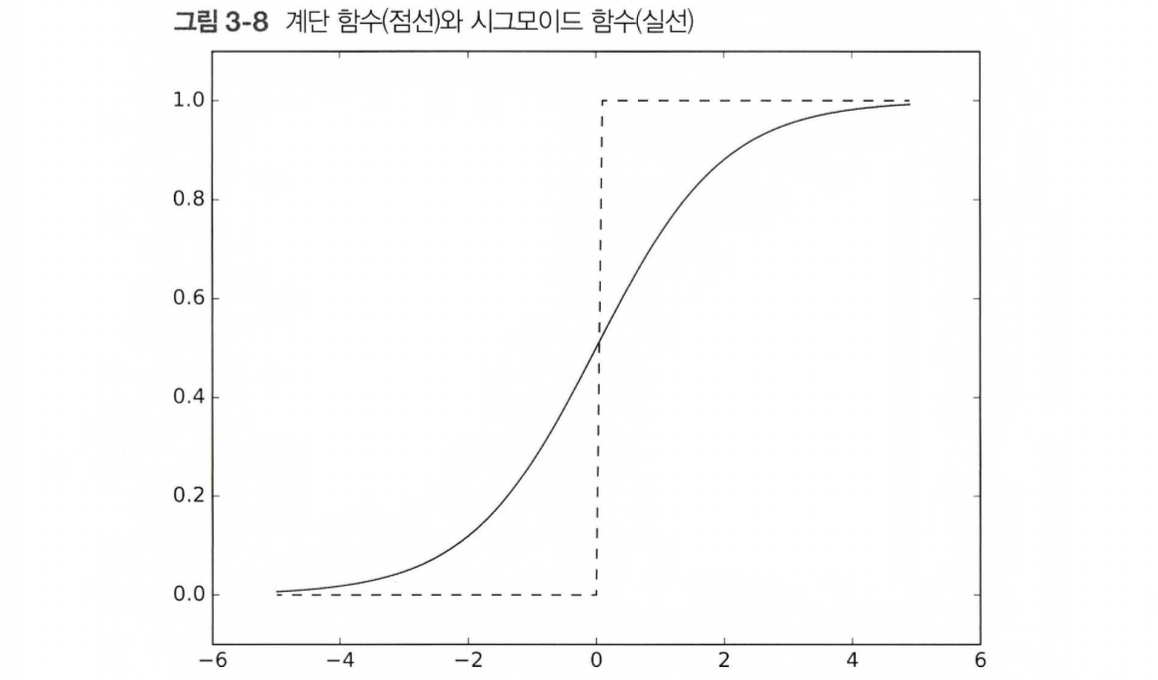
차이점
- 시그모이드 함수는 '매끄러운' 반면, 계단 함수는 출력이 갑자기 바뀌어버린다.(0을 경계로)
- 시그모이드 함수는 실수(0.731, ..., 0.880 등)를 돌려주는 반면 계단함수는 0과 1 중 하나의 값만 돌려준다. 즉, 신경망에서는 '연속적인 실수'가 흐르고, 퍼셉트론에서는 0 혹은 1만 흐른다.
공통점
- 입력이 중요하면 큰 값을 출력하고, 중요하지 않으면 작은 값을 출력한다.
- 비선형 함수이다.
비선형 함수
계단 함수와 시그모이드 함수는 공통적으로 '비선형 함수'인데,
계단 함수는 구부러진 직선, 시그모이드 함수는 곡선으로 나타나기 때문이다.
신경망에서는 활성화 함수로 비선형 함수를 사용해야만 하는데,
선형 함수를 이용하면 신경망의 층을 깊게 하는 의미가 없어지기 때문이다.
의미가 없어지는 이유는,
층을 깊게 만든 네트워크가 '층이 하나밖에 없는(은닉층이 없는) 네트워크' 와 똑같은 기능을 하기 때문이다.
h(x) = c*x 를 활성화 함수(선형함수)로 사용한 3층 네트워크를 생각해보면,
y(x) = h(h(h(x)))로 나타내지는데, 이는 곧 y(x) = c^3*x로 나타내지고,
이는 곧 a = c^3 인 y(x) = a*x와 같게 된다.
즉, 층이 하나밖에 없는(은닉층이 없는) 네트워크로 표현이 된다.
ReLU 함수
최근에는 시그모이드 함수 대신 ReLU(Rectified Linear Unit) 함수를 주로 이용한다.
ReLU는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수이다.
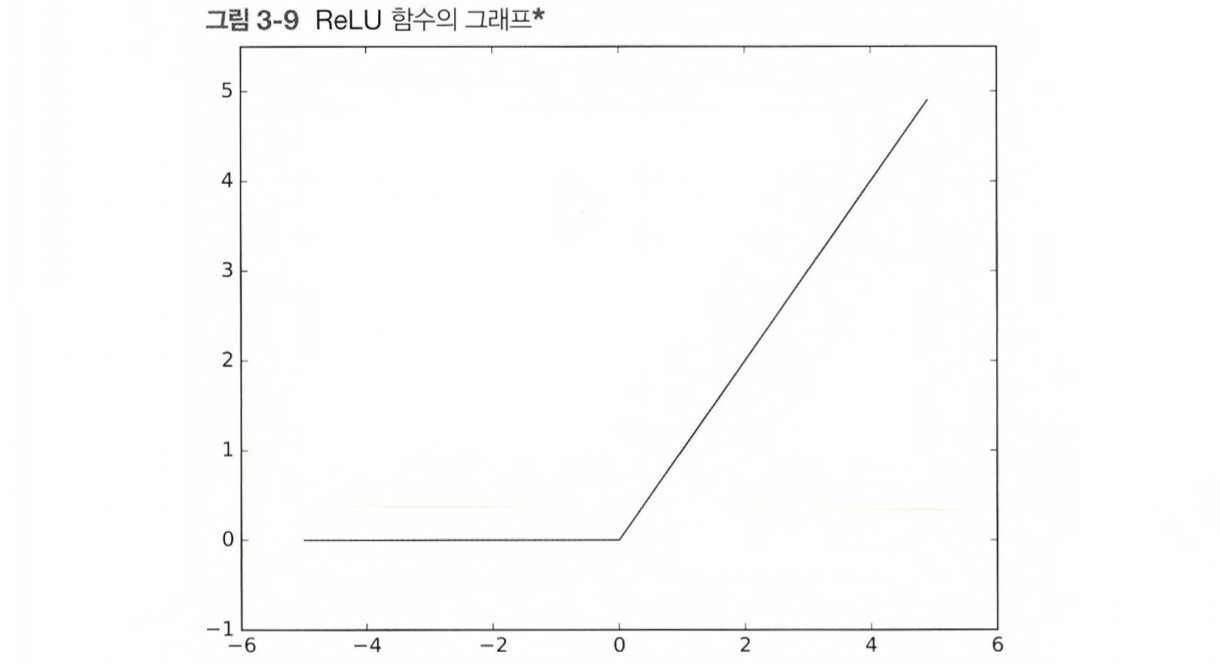
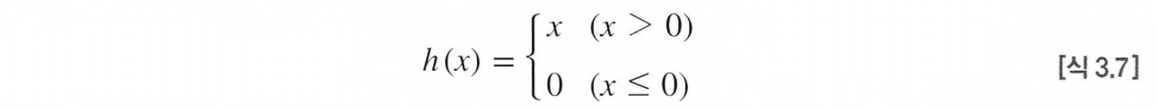
그래프에 수식에서 보이듯이 ReLU는 간단한 함수인데, 구현도 아래와 같이 간단하다.
def relu(x):
return np.maximum(0, x)3.3 다차원 배열의 계산
신경망을 구현하기에 앞서, 이를 효율적으로 구현하기 위해
넘파이의 다차원 배열을 사용한 계산법에 대해 알아보자.
다차원 배열
우선 1차원 배열을 작성해보자.
import numpy as np
A = np.array([1, 2, 3, 4])
print(A)
# >>> [1 2 3 4]
np.ndim(A) # 배열의 차원 수 확인
# >>> 1
A.shape # 배열의 형상 확인
# >>> (4,)
A.shape[0]이어서 2차원 배열을 작성해보자.
B = np.array([[1,2], [3,4], [5,6]])
print(B)
# >>> [[1 2]
# [3 4]
# [5 6]]
np.ndim(B) # 배열의 차원 수 확인
# >>> 2
B.shape # 배열의 형상 확인
# >>> (3, 2)알다시피, 위와 같은 2차원 배열은 행렬이라고 부른다.
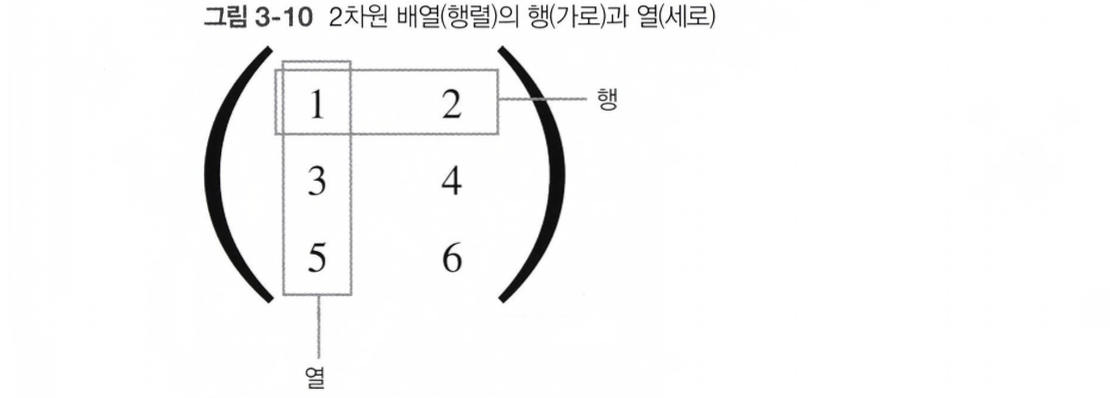
행렬의 곱
알고 있겠지만, 행렬의 곱을 구하는 방법은 아래와 같다.
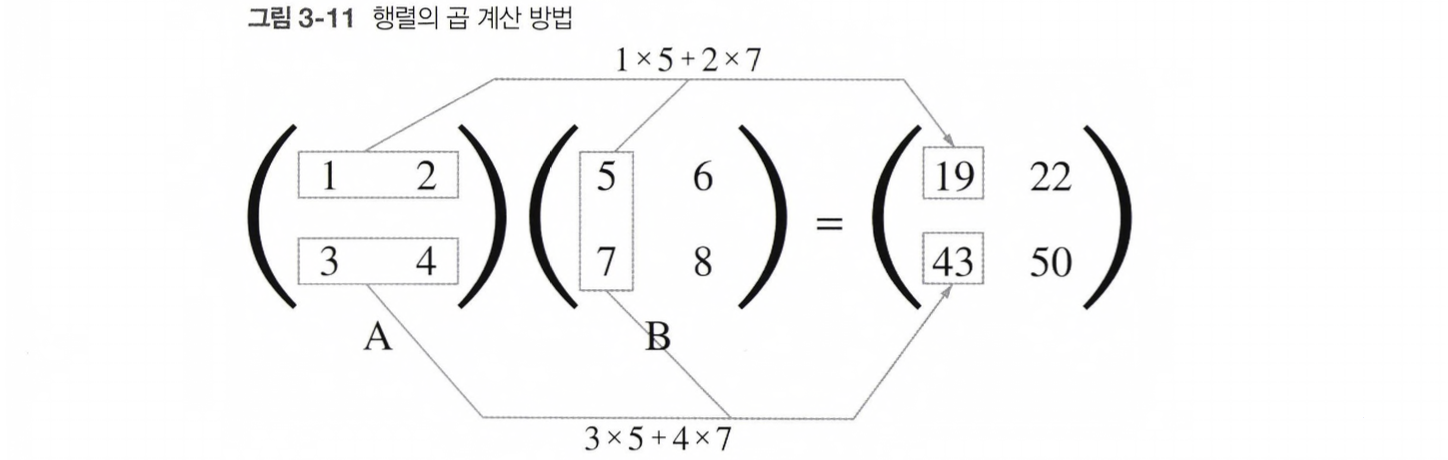
이를 코드로 구현하면 아래와 같다.
"""형상이 2x2로 같은 행렬의 곱"""
A = np.array([[1,2], [3,4]])
A.shape
# >>> (2, 2)
B = np.array([[5,6], [7,8]])
B.shape
# >>> (2, 2)
np.dot(A, B) # 행렬의 곱 연산
# >>> array([[19, 22],
# [43, 50]])
"""형상이 2x3 과 3x2로 다른 행렬의 곱"""
A = np.array([[1,2,3], [4,5,6]])
A.shape
# >>> (2, 3)
B = np.array([[1,2], [3,4], [5,6]])
B.shape
# >>> (3, 2)
np.dot(A, B) # 행렬의 곱 연산
# >>> array([[22, 28],
# [49, 64]])
"""🚨 형상이 2x2 와 2x3 으로 차원의 원소 수가 일치하지 않는 행렬의 곱 -> 오류🚨"""
C = np.array([[1,2], [3,4]])
C.shape
# >>> (2, 2)
A.shape
# >>> (2, 3)
np.dot(A, C)
# >>>
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-41-bb5afb89b162> in <cell line: 1>()
----> 1 np.dot(A, C)
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)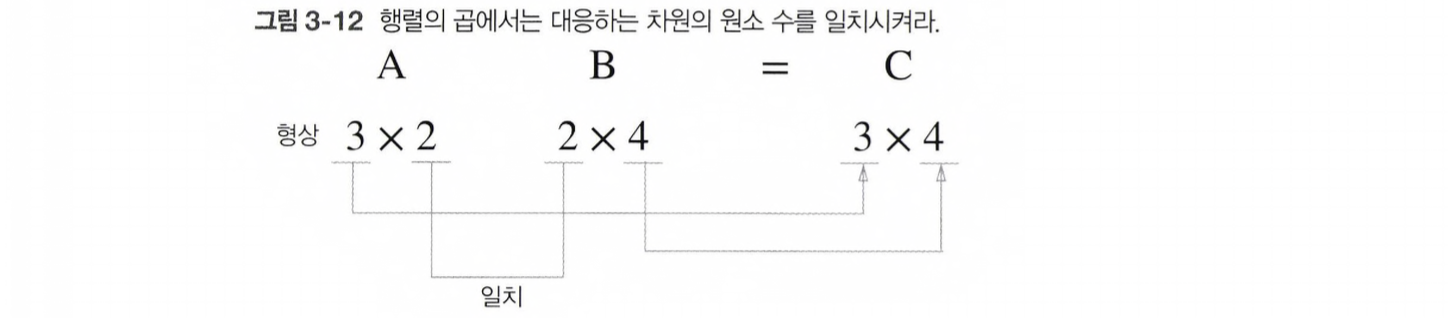

[그림 3-13]을 구현하면 아래와 같다.
A = np.array([[1,2], [3,4], [5,6]])
A.shape
# >>> (3, 2)
B = np.array([7,8])
B.shape
# >>> (2,)
np.dot(A, B) # 행렬의 곱 연산
# >>> array([23, 53, 83])신경망에서의 행렬 곱
넘파이 행렬을 사용해서, 편향과 활성화 함수를 생략한 간단한 신경망을 구현해보자.
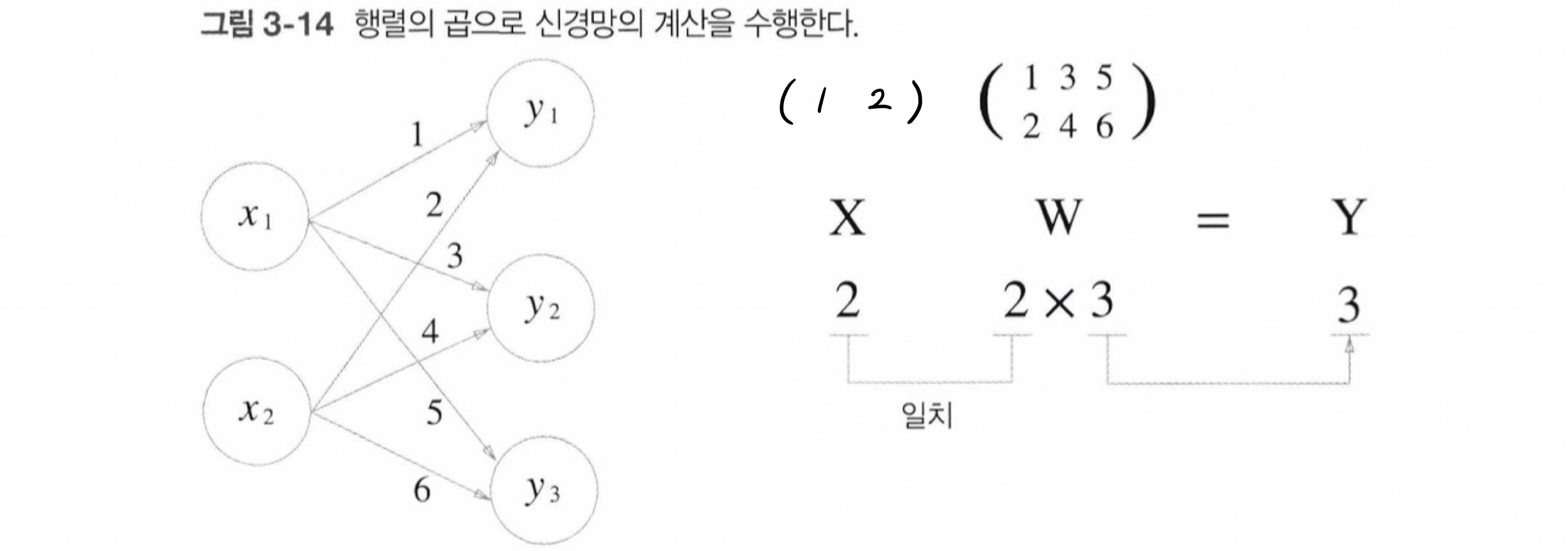
X = np.array([1,2])
X.shape
# >>> (2,)
W = np.array([[1,3,5], [2,4,6]])
print(W)
# >>> [[1 3 5]
# [2 4 6]]
W.shape
# >>> (2, 3)
Y = np.dot(X, W)
print(Y)
# >>> [ 5 11 17] np.dot 함수를 사용하면 Y의 원소가 몇 만개이던 한 번의 연산으로 결과를 계산할 수 있다.
그렇기에 신경망을 구현할 때 행렬의 곱으로 한번에 계산해주는 기능이 아주 중요하다!
3.4 3층 신경망 구현하기
이제 좀 더 본격적으로, 3층 신경망에서 수행되는 입력부터 출력까지의 처리(순방향)를 구현해보자.
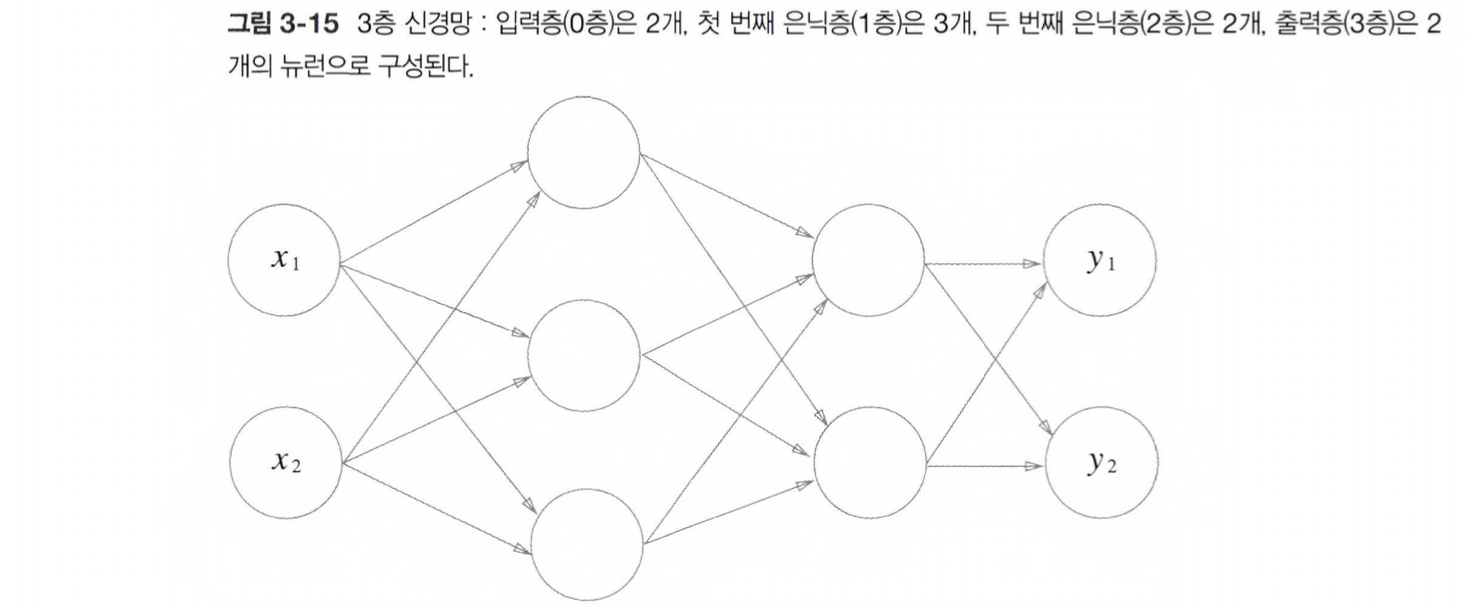
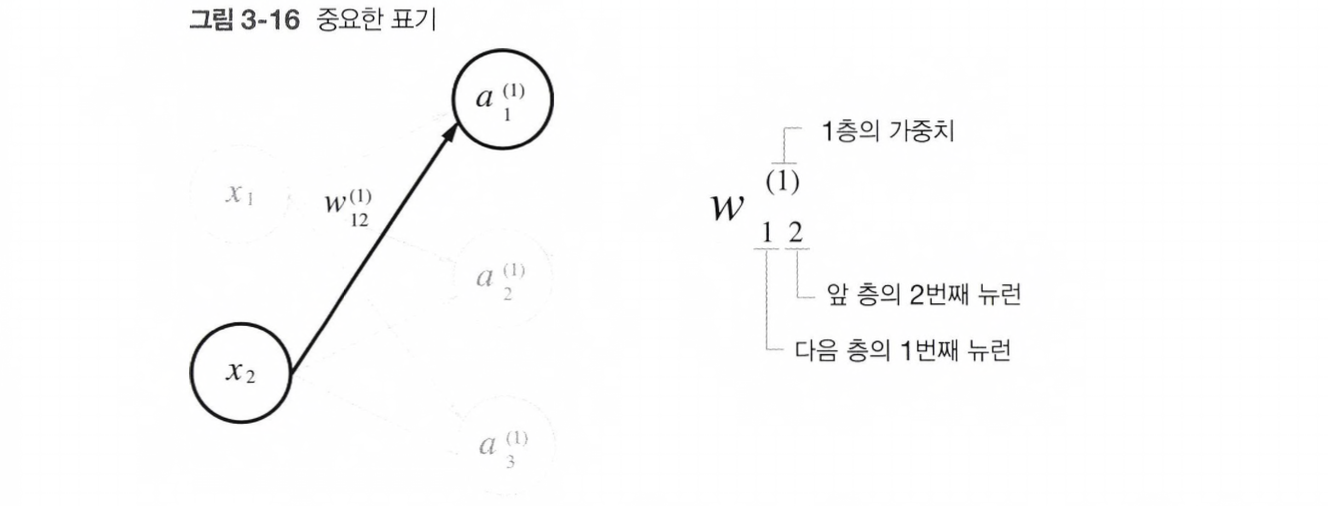
표기법 설명
각 층의 신호 전달 구현하기
먼저, '입력층 -> 1층의 첫번째 뉴런' 으로 가는 신호를 살펴보자.
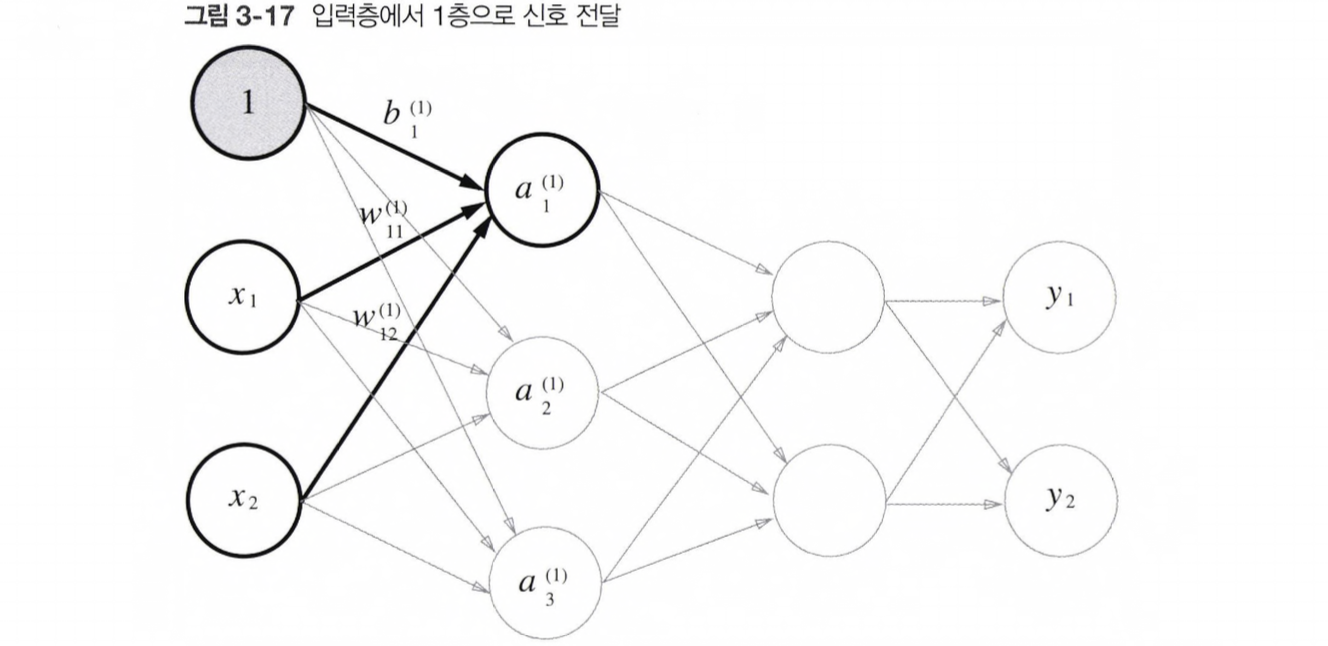
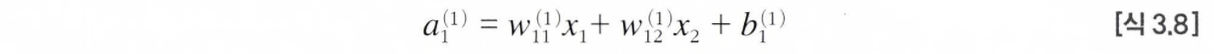
행렬의 곱을 이용하면 1층의 '가중치 부분'을 아래처럼 간소화 할 수 있다.

이때 각 표기는 아래와 같다.
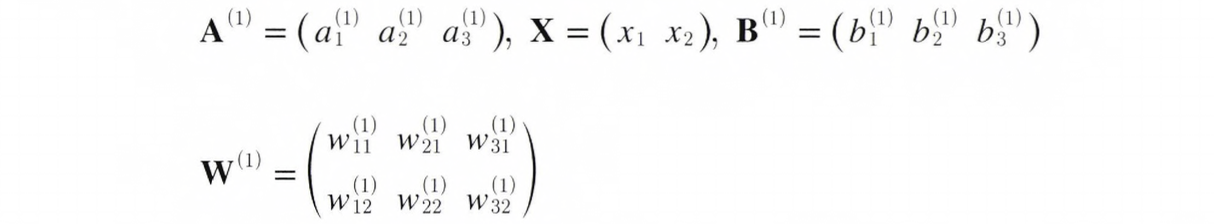
그럼 [식 3.9]를 코드로 구현해보자.
""" 입력층 -> 1층 가중치 부분 """
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape) # >>> (2, 3)
print(X.shape) # >>> (2,)
print(B1.shape) # >>> (3,)
A1 = np.dot(X, W1) + B1이어서 1층의 '활성화 함수'에서의 처리를 살펴보자.
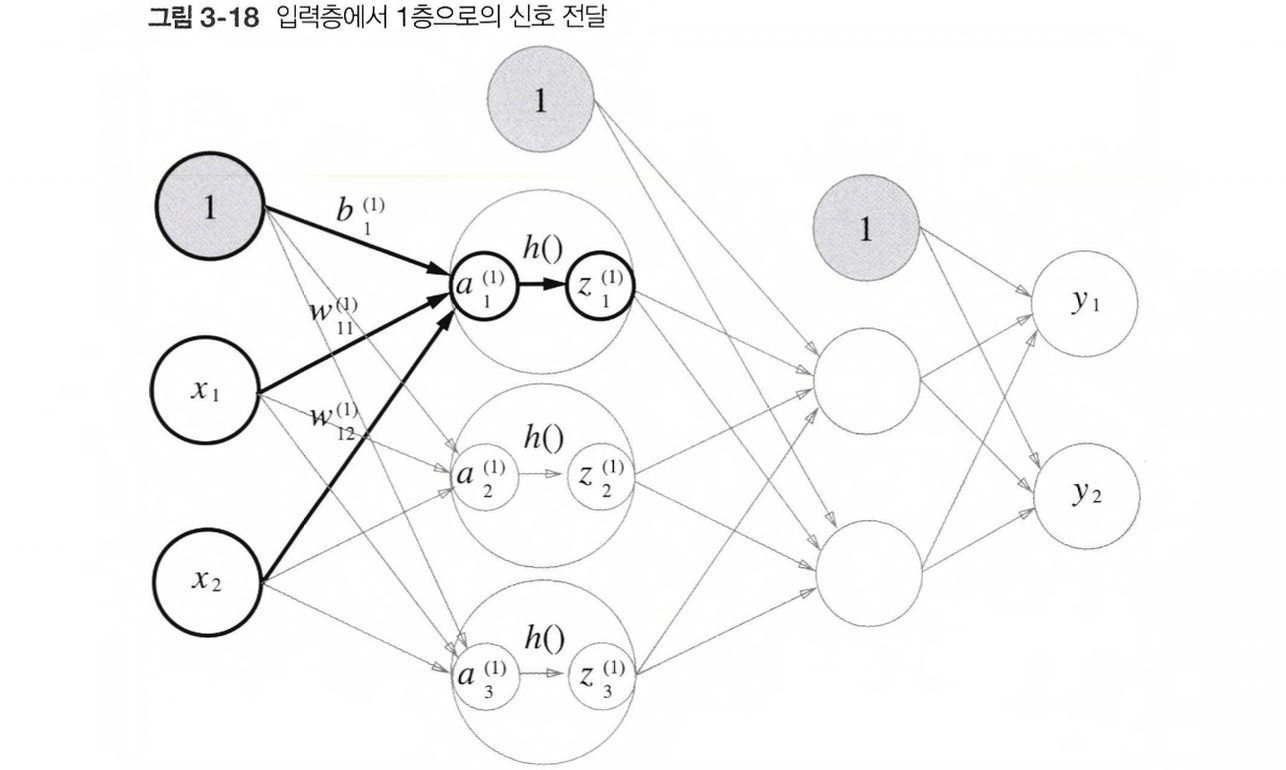
이를 코드로 구현하면 아래와 같다.
""" 입력층 -> 1층 활성화 함수 부분 """
Z1 = sigmoid(A1)
print(A1) # >>> [0.3 0.7 1.1]
print(Z1) # >>> [0.57444252 0.66818777 0.75026011]이제 1층에서 2층으로의 신호 전달 과정과 구현을 살펴보자.
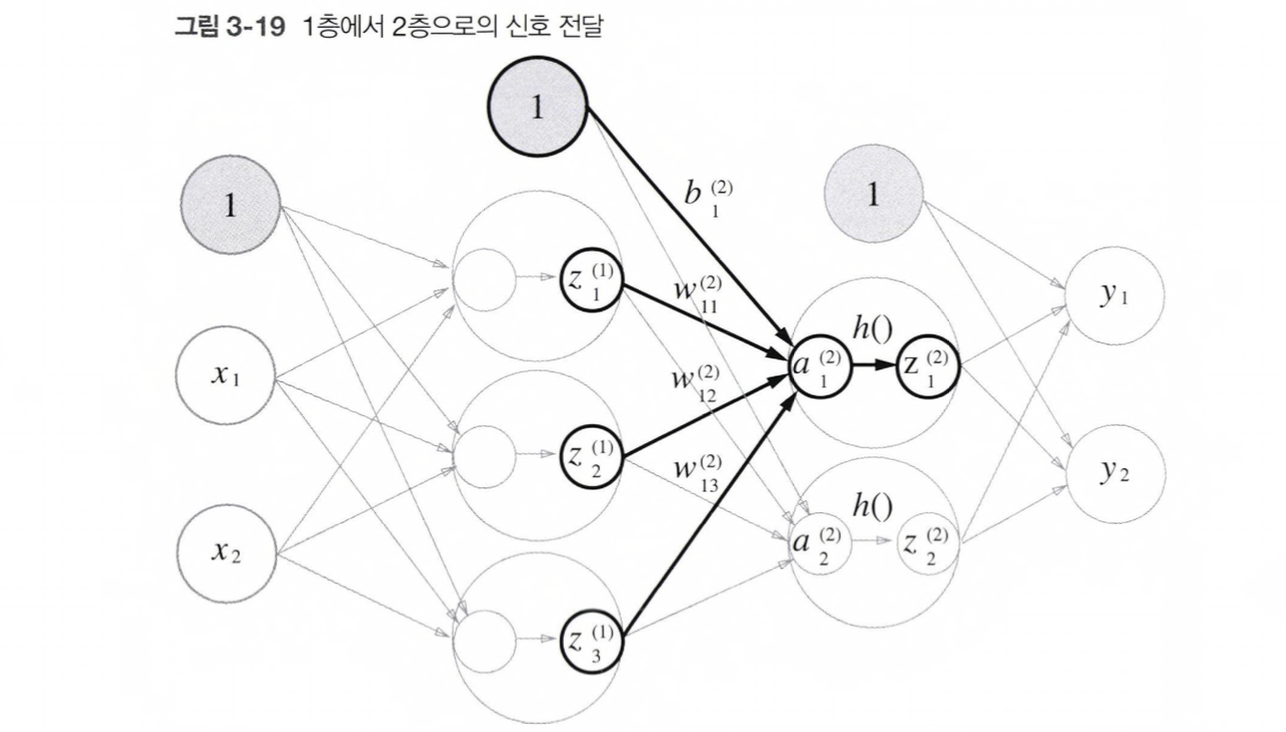
""" 1층 -> 2층 신호 전달 """
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape) # >>> (3,)
print(W2.shape) # >>> (3, 2)
print(B2.shape) # >>> (2,)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)마지막으로 2층에서 출력층으로의 신호 전달 과정과 구현을 살펴보자.
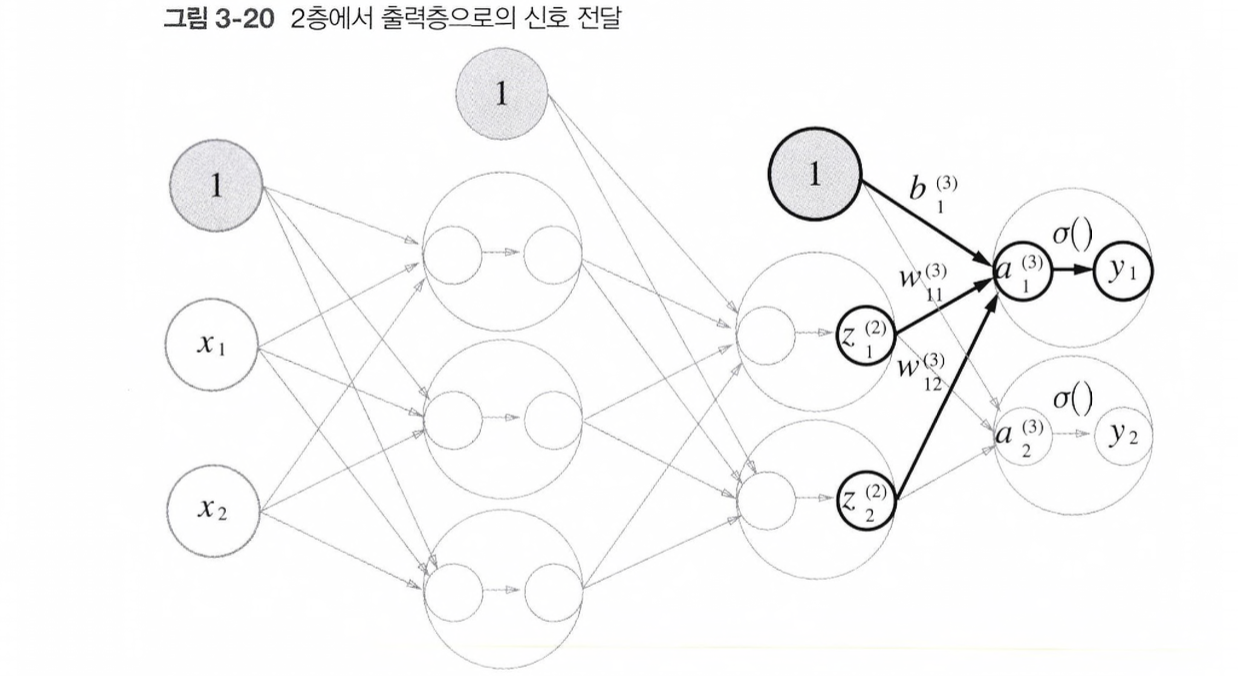
""" 2층 -> 3층 신호 전달 """
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3) # 혹은 Y = A3지금은 신경망의 출력층에 항등 함수인 identity_function() 을 정의하고 사용했지만,
실제로는 모델이 풀고자 하는 문제의 성질에 맞게 활성화 함수를 적용한다.
회귀에는 항등 함수를,
2 클래스 분류 (이중 분류)에는 시그모이드 함수를,
다중 클래스 분류(다중 분류)에는 소프트맥스 함수를 사용한다.
구현 정리
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) #2*3
network['b1'] = np.array([0.1, 0.2, 0.3]) #1*3
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) #3*2
network['b2'] = np.array([0.1, 0.2]) #1*2
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]]) #2*2
network['b3'] = np.array([0.1, 0.2]) #1*2
return network
#신호가 순방향(입력에서 출력 방향)으로 전달됨(순전파)임을 알리기 위함이다.
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5]) #1*2
y = forward(network, x)
print(y)3.5 출력층 설계하기
신경망에서 출력층에 사용되는 활성화 함수에 따라 회귀인지 분류인지가 나뉘어진다.
(일반적으로)
회귀 -- 항등함수
분류 -- 소프트맥스
항등 함수와 소프트맥스 함수 구현
회귀에 사용되는 항등 함수는 입력을 그대로 출력하기 때문에 아래의 그림과 같이 나타난다.
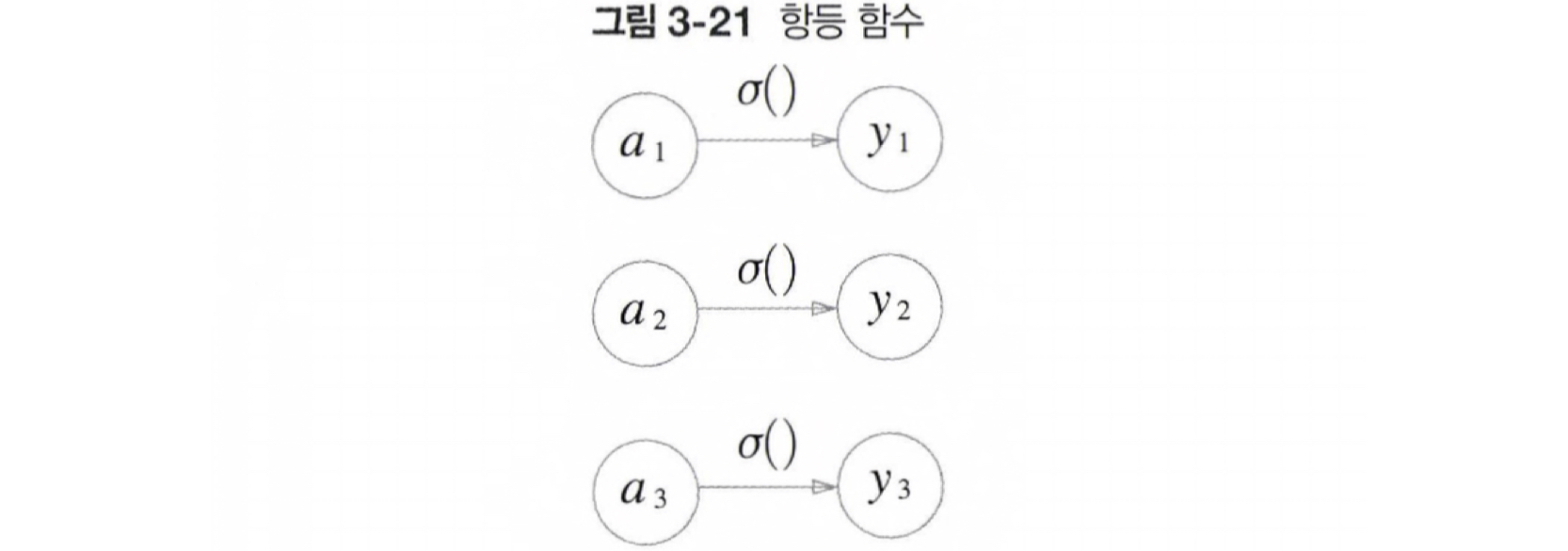
분류에 사용되는 소프트맥스 함수를 나타내는 식은 아래와 같은데,
(n = 출력층의 뉴런 수, yk = 그 중 k번째 출력, ak = k번째 입력 신호)
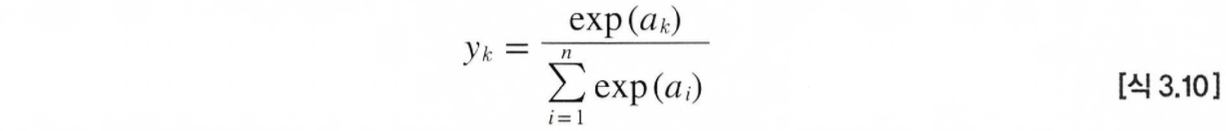
출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문에, 이를 그림으로 나타내면 아래와 같다.
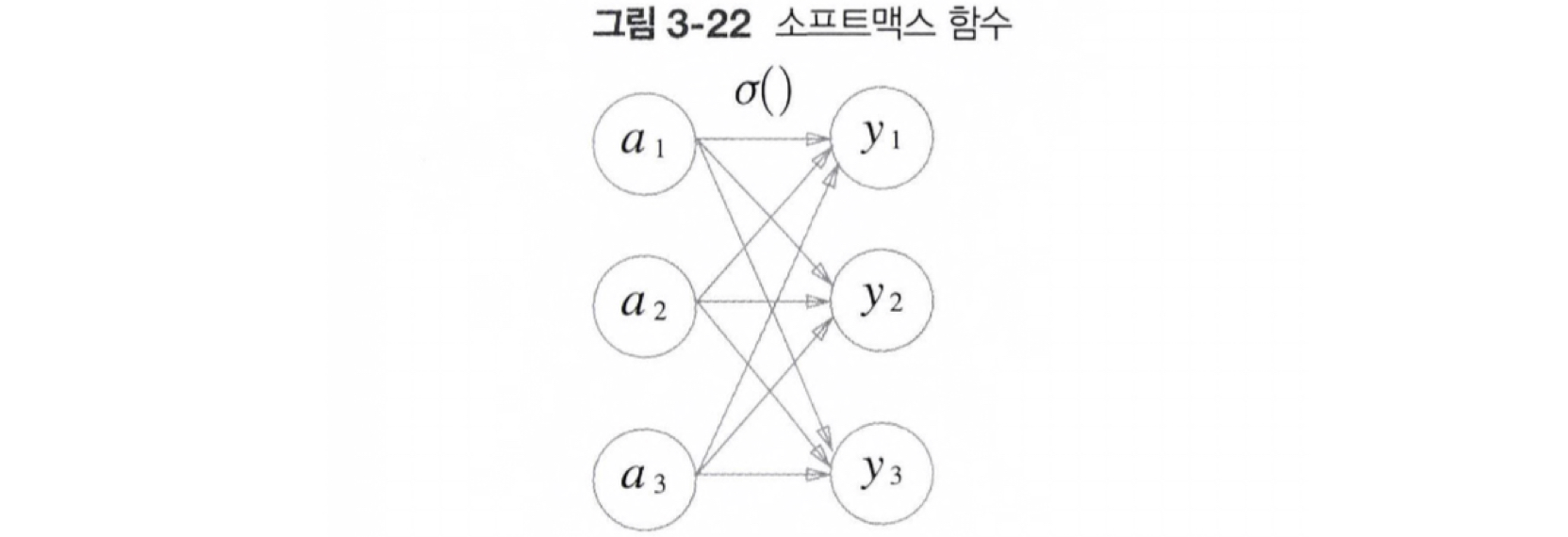
그럼 위의 소프트 맥스 함수를 구현해보자.
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y소프트맥스 함수 구현 시 주의점
위에서 구현한 코드는 지수함수 e 때문에 오버플로의 문제가 있다.
지수 함수는 쉽게 매우 큰 값을 내뱉는다.
e^100은 0이 40개가 넘는 큰 값이 되고, e^1000은 무한대를 뜻하는 inf를 내뱉는다.
이렇게 큰 값끼리 나눗셈을 하면 결과 수치가 불안정해진다
이 문제를 해결하기 위해
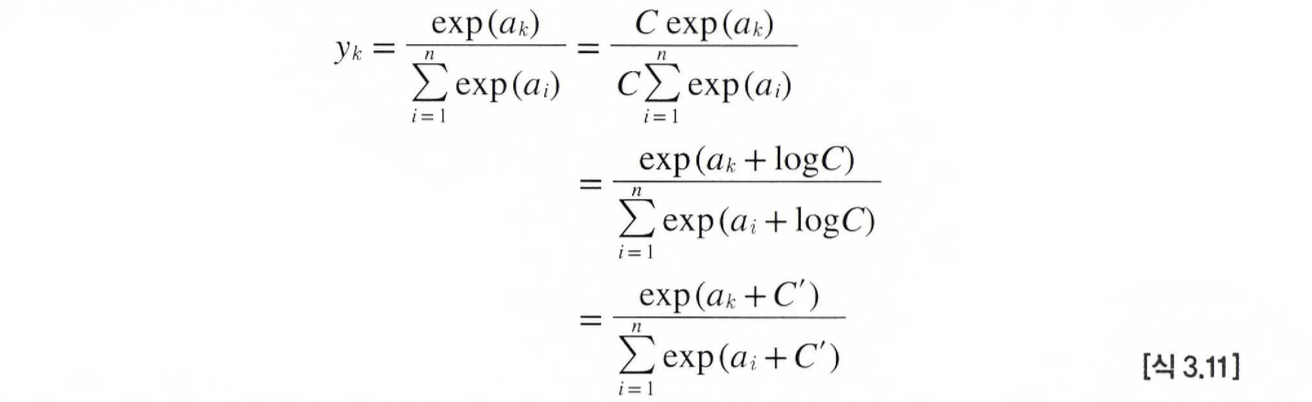
위와 같이 식을 바꿔주는데, 여기서 C'에 어떤 값을 대입해도 상관없지만, 오버플로를 막을 목적으로는 입력 신호 중 최댓값에 (-)를 붙여 이용하는 것이 일반적이다.
아래 예시를 통해 확인해보자.
a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a))
# >>> array([nan, nan, nan]) # 🚨 큰 값들의 나눗셈이라 제대로 계산되지 않는다! 🚨
c = np.max(a)
a - c
# >>> array([ 0, -10, -20])
np.exp(a - c) / np.sum(np.exp(a - c))
# >>> array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09]) # 올바르게 계산된다!이렇게 수정한 뒤에 소프트맥스 함수를 다시 구현해보자.
def softmax(a):
c = np.max(a)
exp_a = np(np.exp(a - c)) # 오버플로 방지
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y소프트맥스 함수의 특징
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
# >>> [0.01821127 0.24519181 0.73659691]
np.sum(y)
# >>> 1.0각각의 출력은 0~1 사이의 실수이고, 총합은 1이 된다는 성질이 있다.
이 덕분에 소프트맥스 함수의 출력을 '확률'로 해석할 수 있다!
위의 예시에서 '0번째 클래스는 1.8%, 1번째 클래스는 24.5%, 2번째 클래스는 73% 이므로,
2번째 클래스가 가장 확률이 높아 분류의 답은 2번째 클래스이다' 라고 해석된다.
그리고, 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않기 때문에,
결과적으로, 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 된다!
기계학습은 '학습' 과 '추론' 의 두 단계를 거쳐 이뤄지는데,
학습단계에서는 출력층에서 소프트맥스 함수를 사용해야하고,
추론단계에서는 출력층에서 소프트맥스 함수를 생략해도 된다. (성능을 위해 다들 생략한다)
출력층의 뉴런 수 정하기
출력층의 뉴런 수는 풀려는 문제에 맞게 적절히 정해야 하는데,
분류에서는 분류하고 싶은 클래스의 수로 설정하는게 일반적이다.
ex) 입력 이미지를 숫자 0~9 중 하나로 분류하는 문제라면 아래와 같이 출력층 뉴런을 10개로 설정한다.
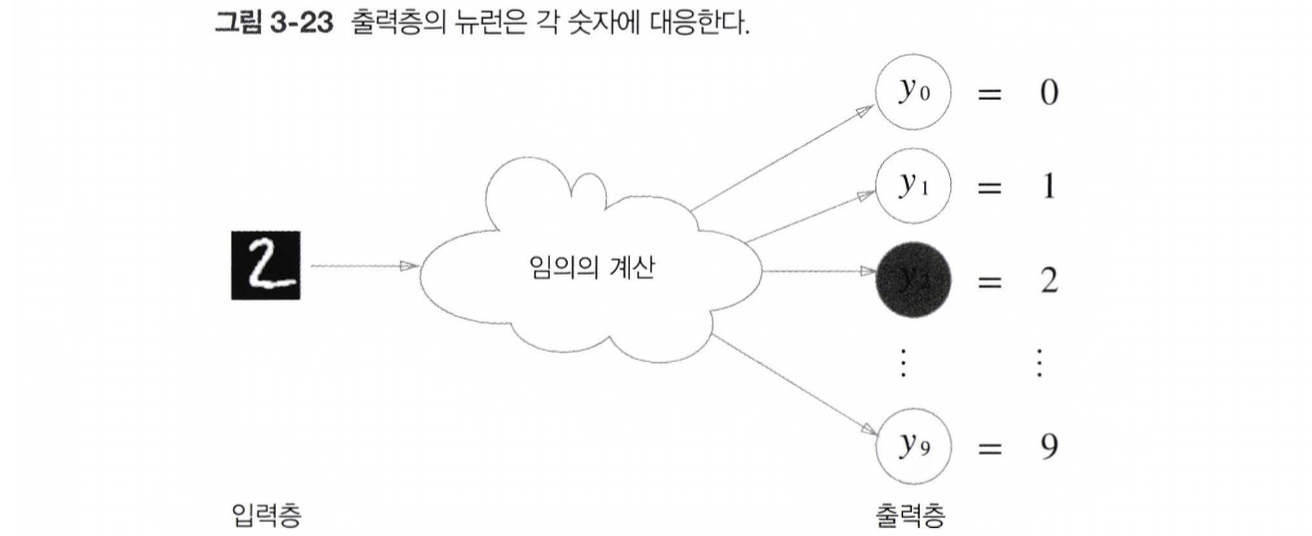
3.6 손글씨 숫자 인식
신경망도 기계학습과 동일하게 훈련과 추론과정을 거치는데,
훈련과정에서는 순전파 후에 역전파를 통해 가중치를 조정하지만,
추론과정에서는 순전파를 통해 단순히 예측을 계산하기만 한다.
MNIST 데이터셋

MNIST는 아주 유명한 데이터 셋으로, 손글씨 숫자 이미지들의 집합이다.
MINIST 데이터셋은 28x28 크기의 회색조 이미지이다.
아래 코드에서 데이터를 확인해보자.
+) Colab에서 교재의 MNIST 데이터셋 사용하는 방법
코랩에서 노트를 하나 만들어서 아래의 코드를 각 셀에 작성하고 실행하면
내 구글 드라이브에 교재가 제공하는 깃헙 파일들이 클론되고, 코랩에서 바로 사용 가능하다!from google.colab import drive drive.mount('/content/drive')cd "/content/drive/My Drive"!git clone https://github.com/kchcoo/WegraLee-deep-learning-from-scratchcd WegraLee-deep-learning-from-scratch
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
print(x_train.shape) # 입력 데이터
print(t_train.shape) # 타깃 데이터
print(x_test.shape)
print(t_train.shape)>>> (60000, 784) # 60,000개의 784차원 벡터로 이루어진 2차원 배열
(60000,) # 60,000개의 단일 정수로 이루어진 1차원 배열
(10000, 784)
(60000,)
# 784차원인 이유는 28x28 크기의 이미지를 flatten=True 를 통해 1차원 배열로 평탄하게 만들었기 때문load_mnist의 매개변수
flatten: 입력 이미지를 평탄하게, 즉 1차원 배열로 만들지 정함
normalize: 입력 이미지의 픽셀값을 0.0~1.0 사이의 값으로 정규화할지를 정함
one_hot_label: 레이블을 원-핫 인코딩 형태로 저장할지를 정함
위의 결과를 이해하려면 아래를 참고하면 좋다.
x_train = [
[0, 0, 0, ..., 0, 0, 0], # 1번째 이미지의 픽셀 값 (784개)
[0, 255, 0, ..., 255, 0, 0], # 2번째 이미지의 픽셀 값 (784개)
...
[0, 255, 0, ..., 255, 0, 0] # 60000번째 이미지의 픽셀 값(784개)
]
t_train = [5, 0, ... 7]
# 60000개데이터를 확인해보기 위해 MNIST 이미지를 화면으로 띄워보자.
from matplotlib.pyplot import imshow
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # >>> 5
print(img.shape) # >>> (784,)
img = img.reshape(28, 28) # 형상을 원래 이미지의 크기로 변형
print(img.shape) # >>> (28, 28)
imshow(img)
# 코랩에서 출력하기 위해 PIL을 사용하는 img_show 함수 대신에 pyplot의 imshow를 사용했다.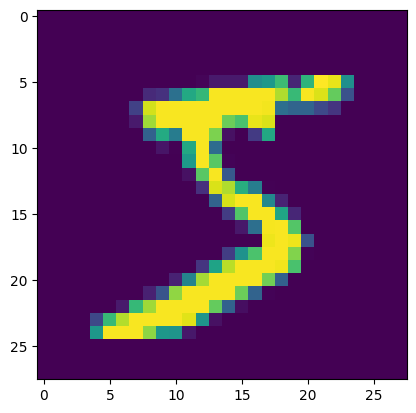
신경망의 추론 처리
이제 이 MNIST 데이터셋을 가지고 추론을 수행하는 신경망을 구현해보자.
입력층 뉴런을 784(28x28)개, 출력층 뉴런을 10(0부터9)개로 설정한다.
2개의 은닉층을 갖는데, 각각 임의로 50개, 100개의 뉴런을 갖도록 설정한다.
import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("/content/drive/My Drive/WegraLee-deep-learning-from-scratch/ch03/sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
w1, w2, w3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, w3) + b3
y = softmax(a3)
return yx, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p = np.argmax(y) # 확률이 가장 높은 원소의 인덱스를 얻는다
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))>>> Accuracy:0.9352추론의 정확도(분류가 얼마나 올바른가)가 93%가 나온다.
이 예에서 load_mnist 함수의 매개변수인 normalize를 True로 설정했는데,
0~255 범위인 각 픽셀의 값을 0.0~1.0 범위로 변환해준다.
이처럼 데이터를 특정 범위로 변환하는 처리를 정규화라고 하고, (스케일을 맞춤 -> 보통 표준편차를 사용)
이렇게 입력 데이터에 특정 변환을 가하는 것을 전처리라고 한다.
배치 처리
이번엔 위의 코드 구현에서 입력 데이터와 가중치 매개변수의 '형상'에 주의를 기울여보자.
x, _ = get_data()
network = init_network()
w1, w2, w3 = network['W1'], network['W2'], network['W3']
x.shape
# >>> (10000, 784)
x[0].shape
# >>> (784,)
W1.shape
# >>> (784, 50)
W2.shape
# >>> (50, 100)
W3.shape
# >>> (100, 10)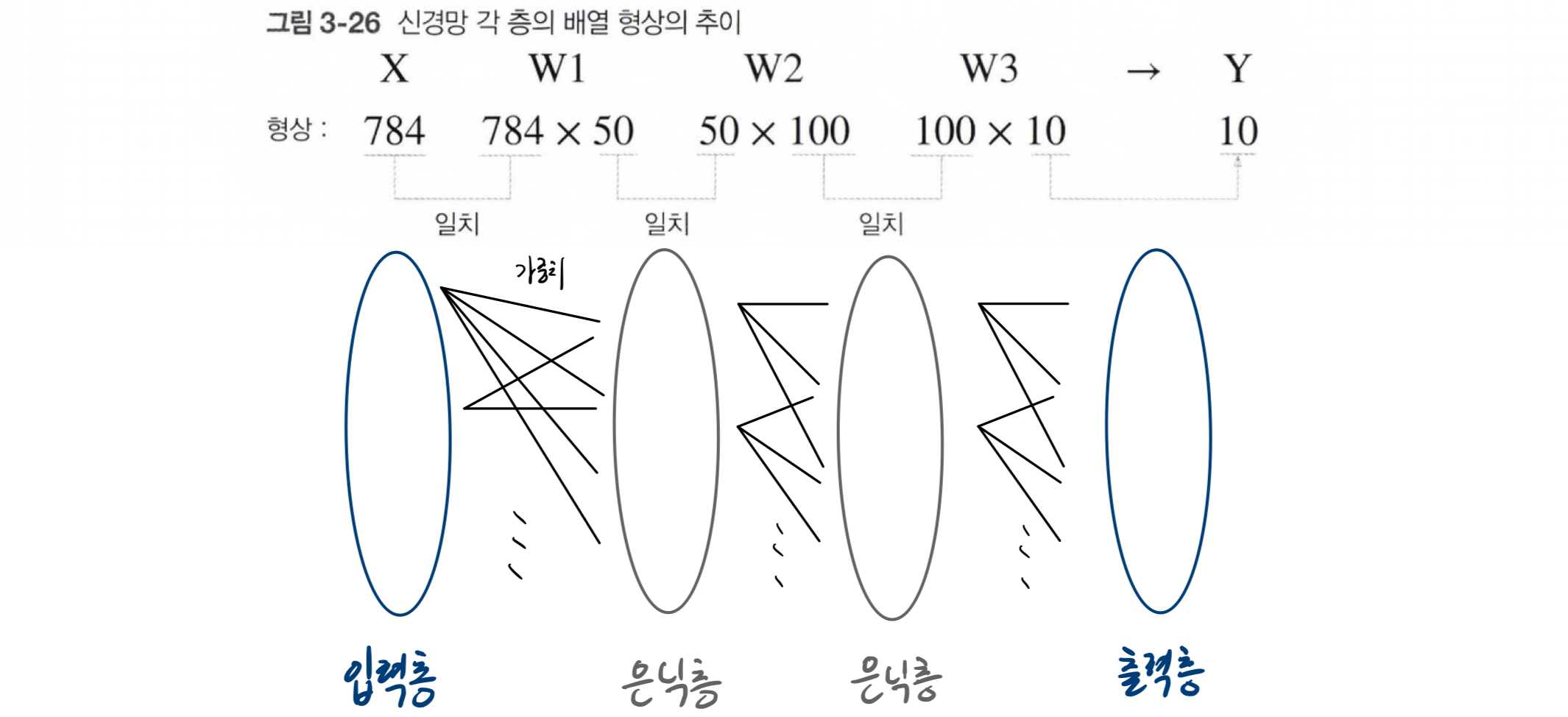
각 층의 가중치 형상을 보면, 다차원 배열의 대응하는 차원의 원소 수가 일치하는 것을 볼 수 있다.
원소가 784개인 1차원 배열이 입력되어 원소가 10개인 1차원 배열이 출력되는 흐름이다.
위는 데이터를 1장만 입력했을 때의 처리 흐름이다.
그러면, 이제 이미지 100장을 한꺼번에 입력하는 경우를 생각해보자.
(이미지 100개를 묶어 predict() 함수에 한번에 넘겨서)
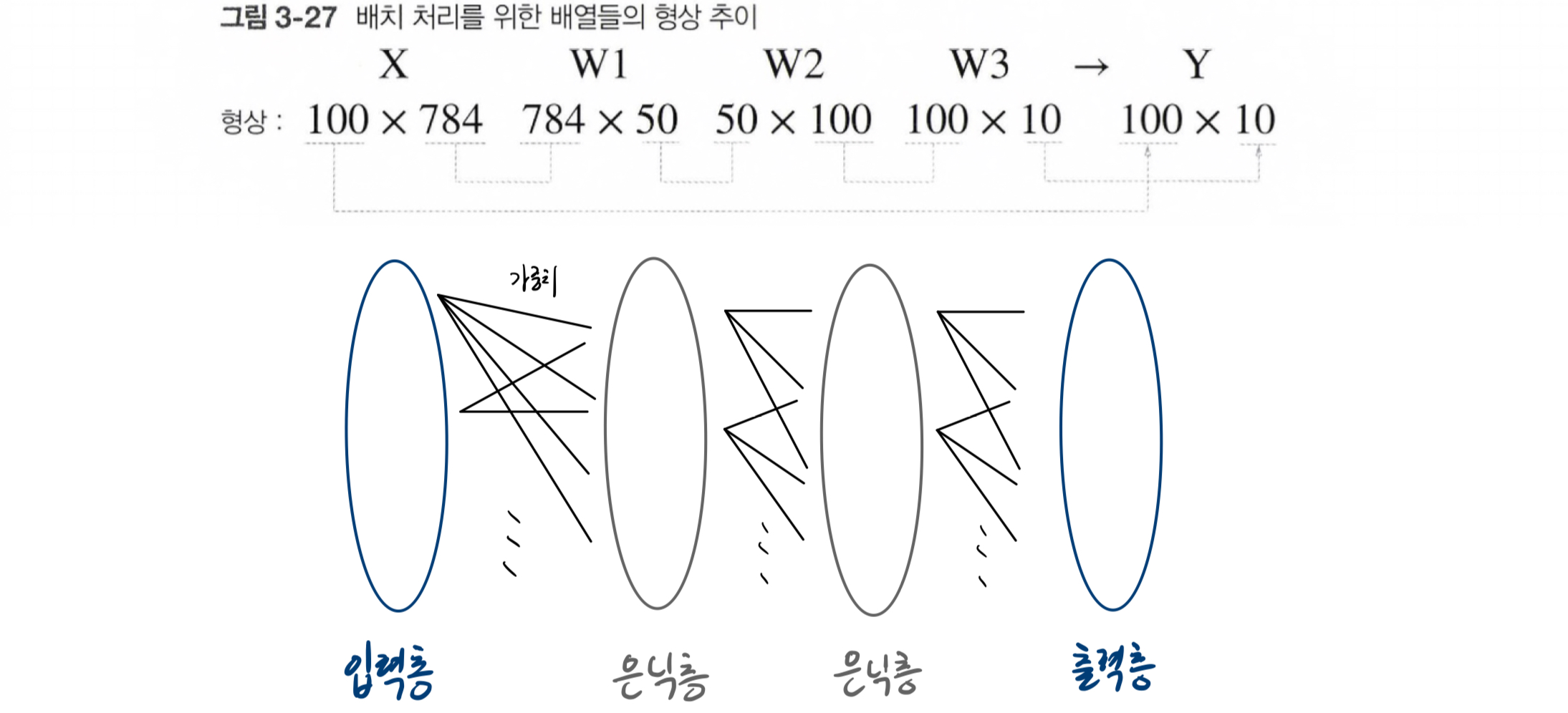
입력 데이터의 형상은 100x784, 출력 데이터의 형상은 100x10이 된다.
즉, 100장 분량의 입력 데이터의 결과가 한 번에 출력된다!
이렇게 하나로 묶은 입력 데이터를 배치(batch)라고 한다.
위에선 이미지가 지폐처럼 다발로 묶여 있다고 생각하면 좋다.
배치 처리를 수행함으로써 큰 배열로 이뤄진 계산을 하게 되는데,
컴퓨터에서는 큰 배열을 한꺼번에 계산하는 것이 분할된 작은 배열을 여러번 계산하는 것보다 빠르기에 처리 시간을 대폭 줄여준다!
그럼 이제 배치 처리를 구현해보자. (위의 코드에서 약간 변형됨!)
x, t = get_data()
network = init_network()
batch_size = 100 # 배치 크기
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))3.7 정리
- 신경망에서는 활성화 함수로 시그모이드 함수와 ReLU 함수 같은 매끄럽게 변화하는 함수를 이용한다
- 넘파이의 다차원 배열을 잘 사용하면 신경망을 효율적으로 구현할 수 있다.
- 기계학습 문제는 크게 회귀와 분류로 나눌 수 있다.
- 출력층의 활성화 함수로는 주로 회귀에서는 항등 함수를, 분류에서는 소프트맥스 함수를 이용한다.
- 분류에서는 출력층의 뉴런 수를 분류하려는 클래스 수와 같게 설정한다.
- 입력 데이터를 묶은 것을 배치라하며, 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있다.