[밑바닥부터 시작하는 딥러닝1] 교재 2장을 기반으로 작성되었습니다.
2.1 퍼셉트론이란?
퍼셉트론이란 신경망(딥러닝)의 기원이 되는 알고리즘이다.
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력하는데,
실제 전류와 달리 퍼셉트론 신호는 '흐른다 / 안 흐른다' 의 두 가지 값만 가진다. (1=흐른다, 0=안 흐른다)
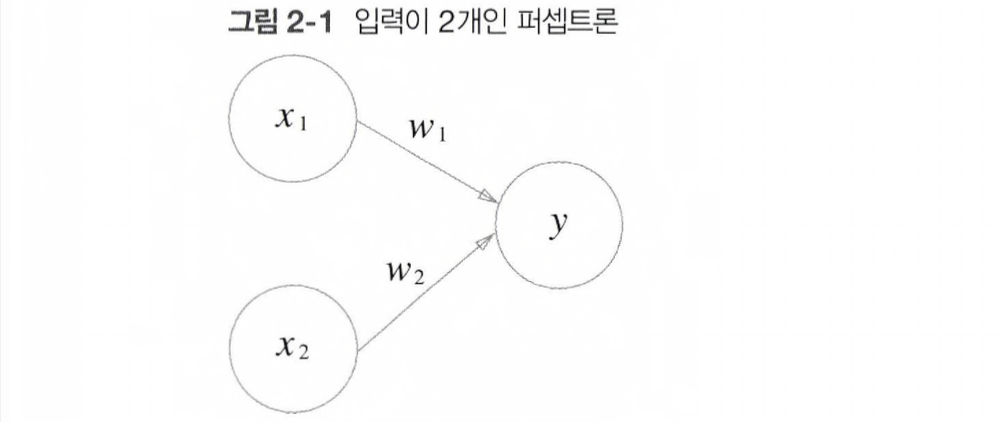
위의 그림에서 x1,x2는 입력 신호, y는 출력 신호, w1,w2는 가중치를 뜻하고 원은 뉴런(노드)라고 부른다.
입력 신호가 뉴런에 보내질 때 각각의 고유한 가중치가 곱해진다.(w1x1, w2x2)
이렇게 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력하는데,
이 한계를 임계값이라 한다. (θ로 표시)
이게 퍼셉트론 동작 원리의 전부인데, 수식으로 나타내면 아래와 같다.
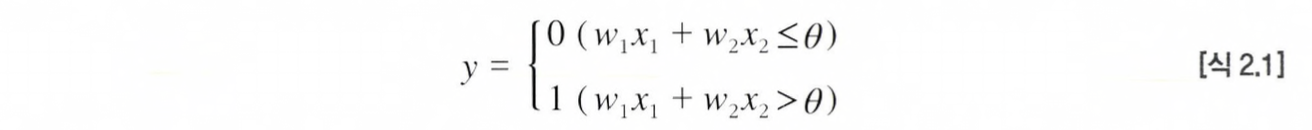
퍼셉트론은 여러 입력 신호에 고유한 가중치를 부여하는데,
가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용한다.
즉, 가중치가 클수록 해당 신호가 중요함을 뜻한다.
2.2 단순한 논리 회로
AND 게이트
퍼셉트론을 활용한 간단한 문제를 살펴보자. 아래는 AND 게이트의 진리표이다.
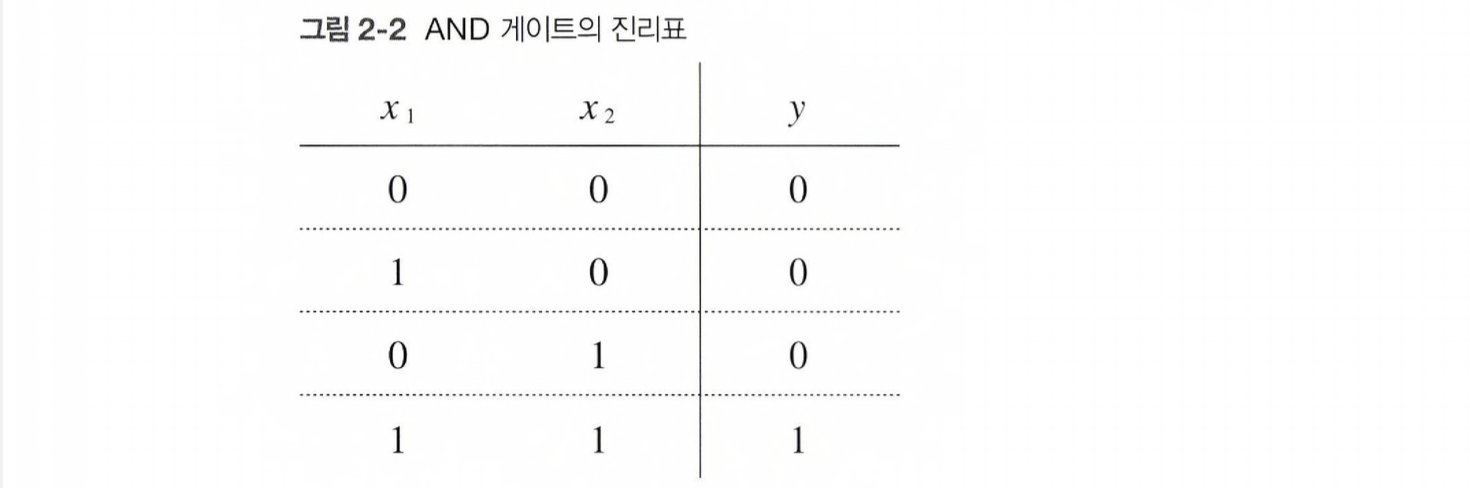
이 AND 게이트를 퍼셉트론으로 표현하고자 한다.
가장 먼저 할 일은 진리표대로 작동하는 w1, w2, θ의 값을 정하는 것이다.
사실 만족하는 매개변수 조합은 무수히 많다. (w1, w2, θ) = (0.5, 0.5, 0.7) or (1.0, 1.0, 1.0) or . . .
이렇게 설정하면 x1, x2가 모두 1일때만 가중 신호의 총합(w1x1 + w2x2)이 주어진 임계값(θ)보다 크게 된다.
NAND 게이트와 OR 게이트
아래는 NAND 게이트의 진리표이다.
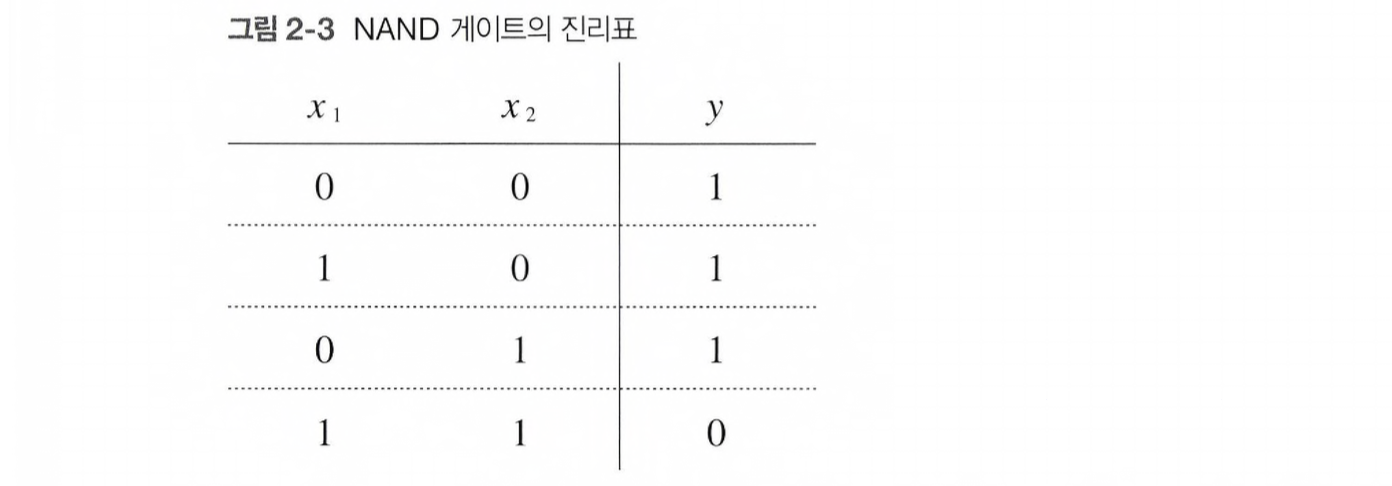
NAND 게이트를 표현하려면 (w1, w2, θ) = (-0.5, -0.5, -0.7) 과 같은 조합이 있다.
사실, NAND 게이트는 Not AND 이므로 AND 게이트의 출력을 뒤집은 것이고,
AND 게이트를 구현하는 매개변수의 부호를 모두 반전시키면 NAND 게이트가 된다.
아래는 OR 게이트의 진리표이다.

매개변수를 어떻게 설정하면 OR 게이트를 구현할 수 있을까?
(w1, w2, θ) = (0.5, 0.5, 0.2) 과 같이 설정하면 된다!
이렇게 간단한 문제를 풀어봤는데, 가장 중요한 점은
각각의 다른 게이트들을 구현하는데 퍼셉트론의 구조는 똑같다는 것이다!
똑같은 구조의 퍼셉트론이 매개변수의 값만 적적히 조정하여 AND, NAND, OR로 변신한다.
2.3 퍼셉트론 구현하기
간단한 구현부터
이제 논리회로를 코드로 구현해보자.
# AND 게이트 구현
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1print(AND(0, 0)) # 0 출력
print(AND(0, 1)) # 0 출력
print(AND(1, 0)) # 0 출력
print(AND(1, 1)) # 1 출력가중치와 편향 도입
위에서 구현한 AND 게이트는 직관적이고 알기 쉽지만, 다른 방식으로 수정하고자 한다.
그 전에, [식 2.1]의 θ를 -b로 치환하면 수식은 아래와 같이 바뀐다.
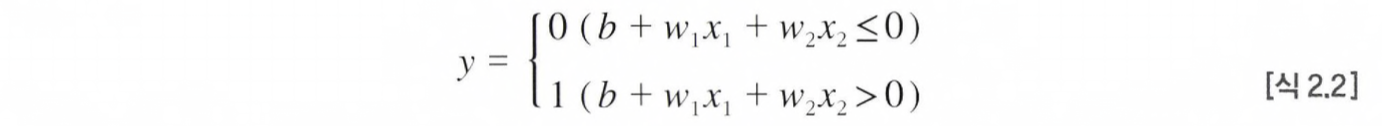
두 가지의 수식은 표기만 바뀌었을 뿐 의미는 같은데, 여기서 b를 편향(bias)라고 한다.
위 수식을 해석해보면 아래와 같다.
'퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력한다.'
이를 파이썬 인터프리터로 순서대로 결과를 확인해보자.
import numpy as np
x = np.array([0, 1])
w = np.array([0.5, 0.5])
b = -0.7
w*x
# >>> array([0. , 0.5])
np.sum(w*x)
# >>> 0.5
np.sum(w*x) + b
# >>> -0.19999999999999996위의 수식대로 계산이 완료된 것을 볼 수 있다.
가중치와 편향 구현하기
이제 '가중치와 편향을 도입한' AND 게이트를 코드로 구현해보자.
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1-θ가 b로 치환되었는데, 여기서 편향 b와 가중치 w1, w2의 기능이 다른 것에 주의하자.
가중치 : 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수
편향 : 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수
이어서 NAND 게이트와 OR 게이트를 구현해보자.
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
# AND와 가중치(w와 b)만 다르다!
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
# AND와 가중치(w와 b)만 다르다!
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 12.4 퍼셉트론의 한계
도전! XOR 게이트
XOR 게이트는 배타적 논리합을 뜻하는 논리회로이다.
x1과 x2가 중 한쪽만 1일때만 1을 출력하는데, 진리표는 아래와 같다.
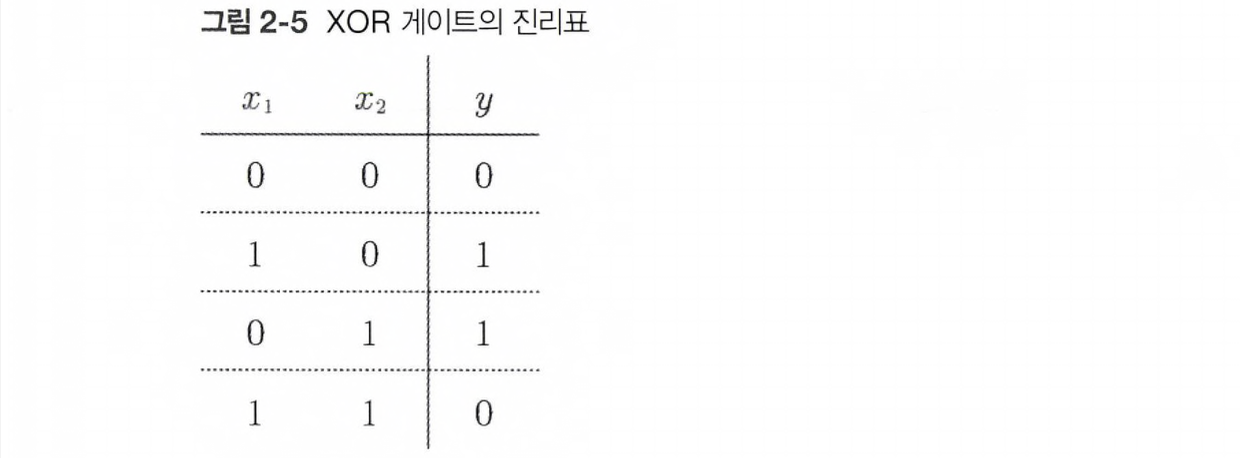
이 XOR 게이트를 퍼셉트론으로 구현하려면 매개변수를 어떻게 설정하면 될까?
사실, 지금까지 공부한 퍼셉트론으론 불가능하다.
불가능한 이유를 OR게이트를 예시로 들며 시각적으로 설명하겠다.
우선, OR 게이트의 퍼셉트론은 아래의 수식으로 표현된다.
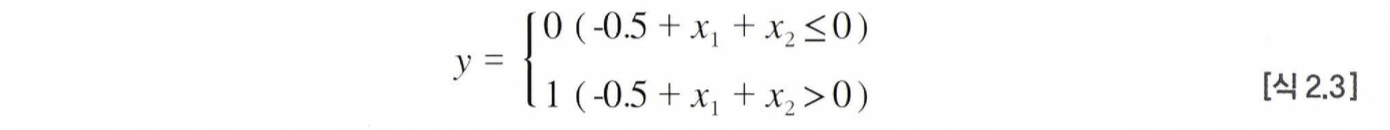
이 퍼셉트론은 아래처럼 직선으로 나뉜 두 영역을 만드는데,
한쪽 영역은 1을 출력하고 다른 한쪽은 0을 출력한다.
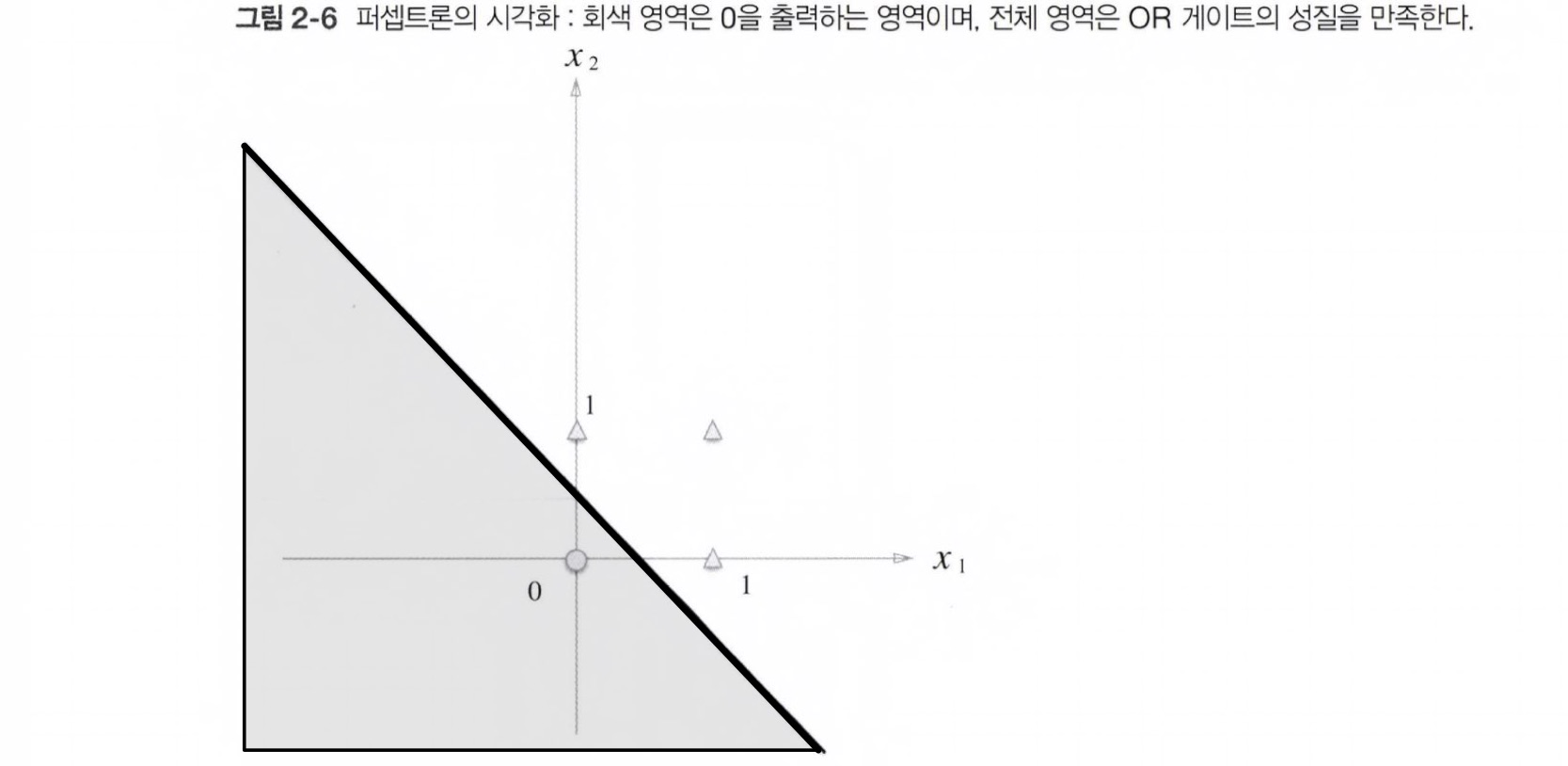
이제 XOR 게이트의 경우를 살펴보자. OR 게이트처럼 직선 하나로 영역을 나눌 수 있을까?
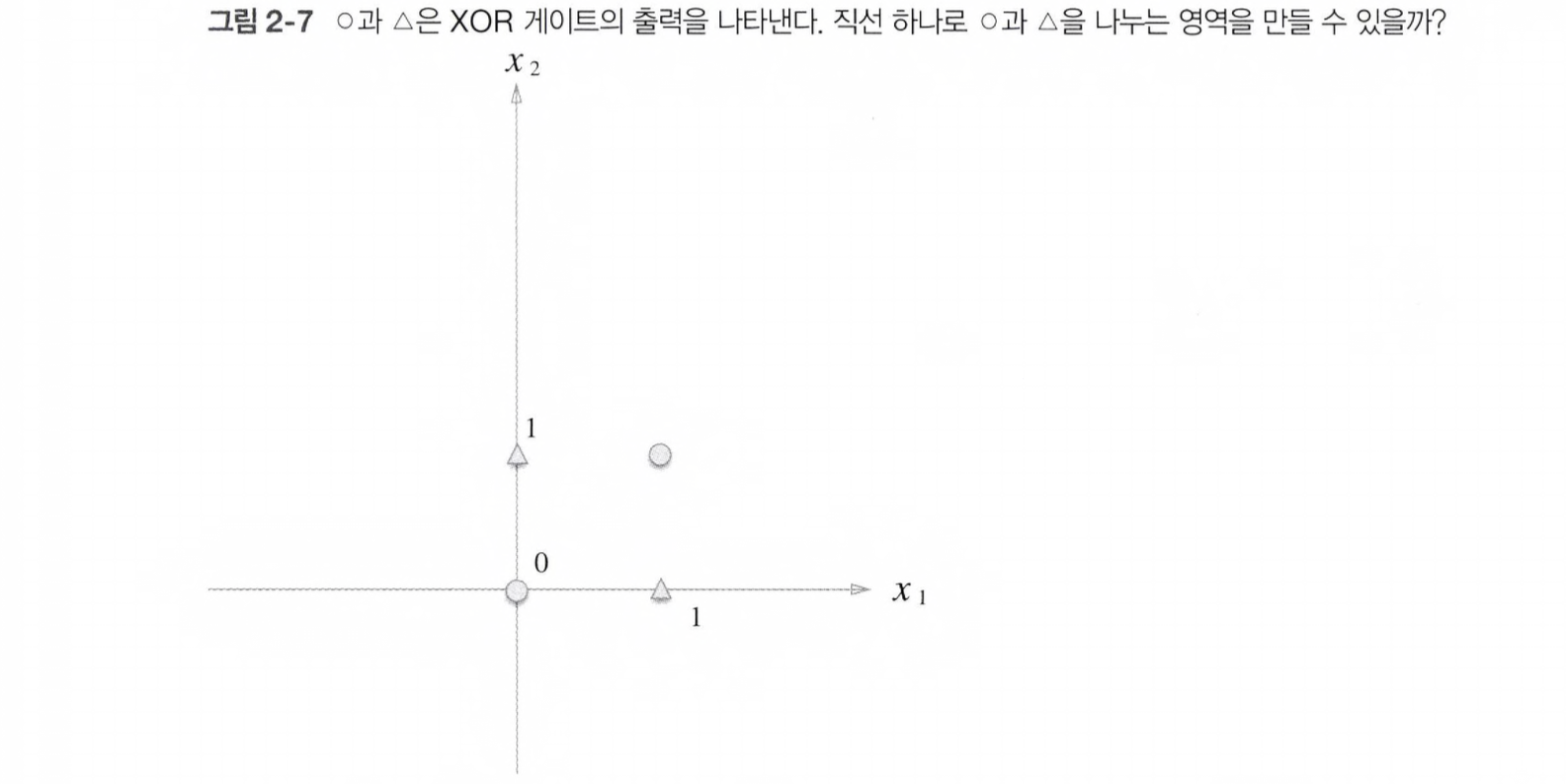
위 그림과 같이 XOR 게이트는 직선 하나로 동그라미와 세모 영역을 나누는 것이 불가능 하다.
선형과 비선형
직선 하나로는 위의 영역을 나눌 수 없지만, '직선'이어야 한다는 제약을 없앤다면 가능하다.
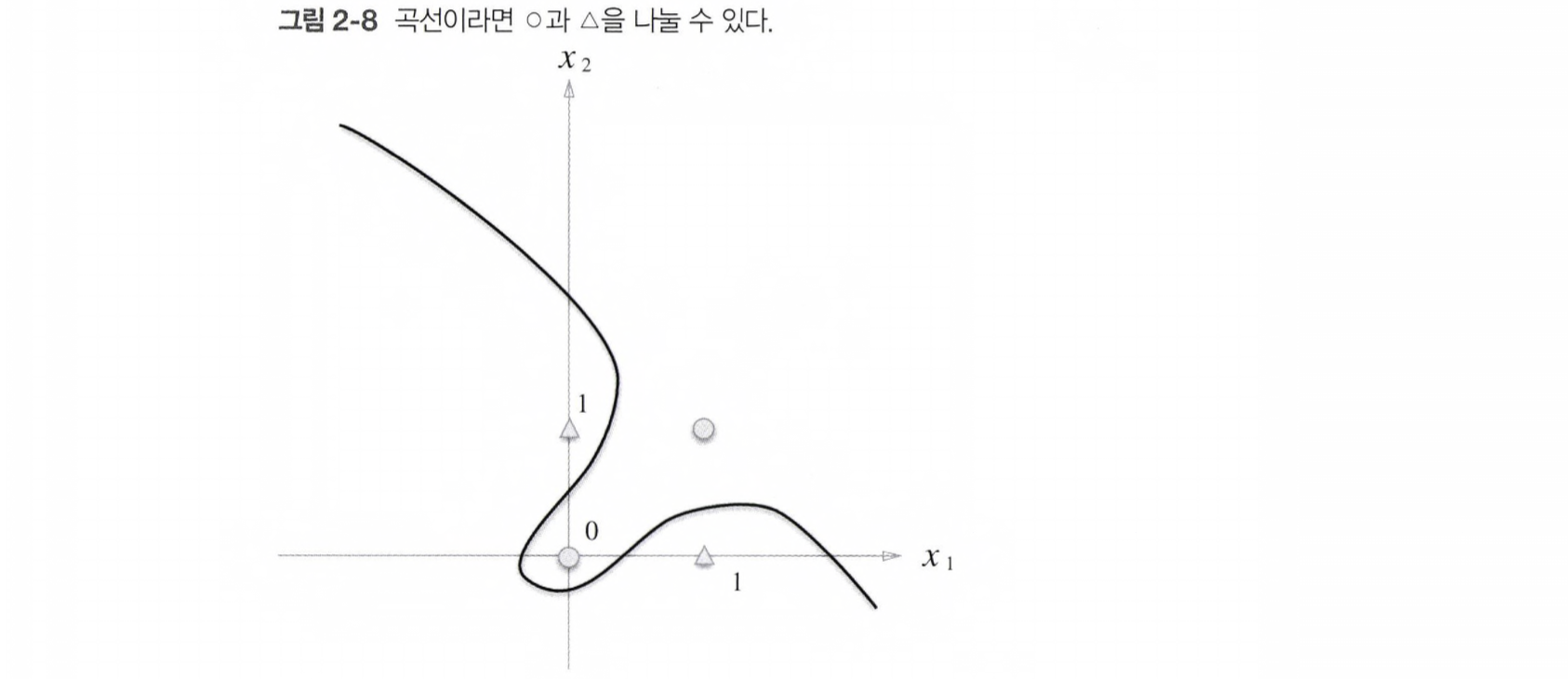
위 그림과 같은 '곡선'의 영역을 비선형 영역 , '직선'의 영역을 선형 영역이라 한다.
이 선형 영역은 '다층 퍼셉트론'이 표현할 수 있다.
2.5 다층 퍼셉트론이 충돌한다면
단층 퍼셉트론으로는 XOR 게이트를 표현할 수 없다.
하지만, 퍼셉트론의 진면모는 '층을 쌓아' 다층 퍼셉트론을 만들 수 있다는데에 있다.
이를 알아보기 전에, XOR 게이트 문제를 다른 관점에서 생각해보자.
기존 게이트 조합하기
XOR 게이트를 만드는 방법 중 하나는 AND, NAND, OR 게이트를 조합하는 방법이 있다.

이 세 가지 게이트를 조합하여 만든 XOR 게이트는 아래와 같다.
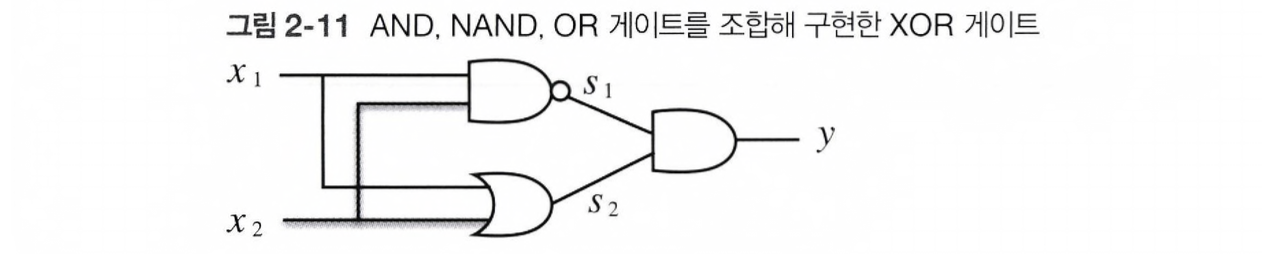
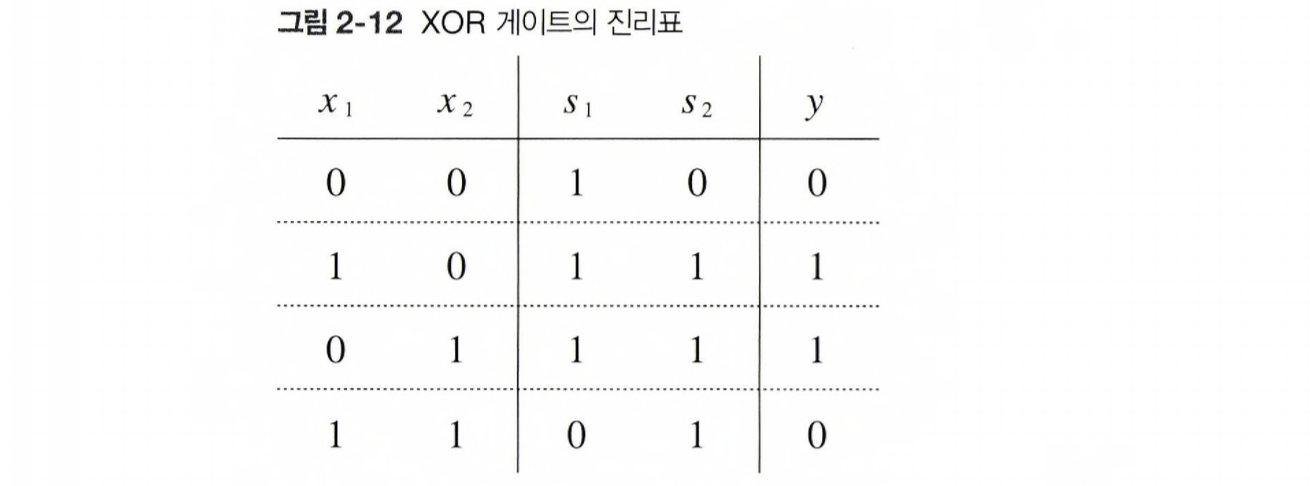
이 논리회로의 진리표는 아래와 같으므로 XOR 게이트를 완성했음을 알 수 있다.
XOR 게이트 구현하기
위와 같이 조합된 XOR 게이트를 코드로 구현해보자. 위에서 구현한 AND, NAND, OR을 사용하면 쉽다.
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return yprint(XOR(0, 0)) # 0을 출력
print(XOR(0, 1)) # 1을 출력
print(XOR(1, 0)) # 1을 출력
print(XOR(1, 1)) # 0을 출력이렇게 성공적으로 구현된 XOR 게이트를 뉴련을 이용한 퍼셉트론으로 표현하면 아래와 같다.
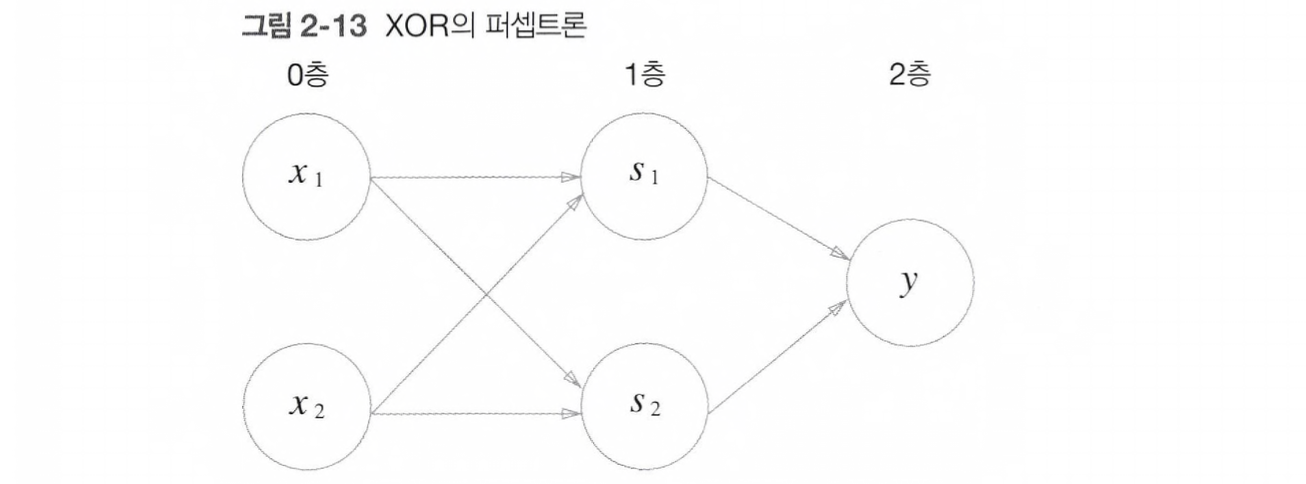
다층 구조의 네트워크를 이루는데, 이처럼 층이 여러 개인 퍼셉트론을 다층 퍼셉트론이라 한다.
단층 퍼셉트론으로는 표현하지 못한 XOR 게이트를 층을 하나 늘려 구현할 수 있게되었다.
이와 같이 퍼셉트론은 층을 쌓아 (깊게 하여) 더 다양한 것을 표현할 수 있다.
2.6 NAND에서 컴퓨터까지
다층 퍼셉트론은 생각보다 더 많이 복잡한 회로를 만들 수 있다.
사실 NAND 게이트의 조합만으로 컴퓨터를 만들 수 있기 때문에, 퍼셉트론으로 컴퓨터를 표현할 수 있다.
그러면 층을 얼마나 깊게 해야 컴퓨터가 만들어 질까?
미친 소리 같지만, 2층 퍼셉트론으로, 정확히는 '비선형인 시그모이드 함수를 활성화 함수로 이용하면' 표현할 수 있다. (활성화 함수는 3장에서 배워보자)
2.7 정리
- 퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- 퍼셉트론에서는 '가중치'와 '편향'을 매개변수로 설정한다.
- 퍼셉트론으로 AND,NAND ,OR 게이트 등의 논리 회로를 표현할 수 있다.
- XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
- 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.
- 단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.
- 다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.
