다이나믹 프로그래밍
중복되는 연산 줄이기
컴퓨터는 연산 속도에 한계가 있고, 메모리 공간을 사용할 수 있는 데이터의 개수도 한정적이라는 점이 많은 제약을 발생시킵니다. 그래서 연산 속도와 메모리 공간을 최대한 활용할 수 있는 효율적인 알고리즘을 작성해야 합니다.
다만, 어떤 문제는 메모리 공간을 약간 더 사용하면 연산 속도를 비약적으로 증가시킬수 있는 방법이 존재하는데, 그게 바로 다이나믹 프로그래밍(Dynamic Programming)입니다.
중복 연산 예시(다이나믹 프로그래밍의 필요성)
다이나믹 프로그래밍으로 해결할 수 있는 대표적인 예시가 파보나치 수열입니다. 파보나치 수열은 이전 두 항의 합을 현재의 항으로 설정하는 특징이 있는 수열입니다.
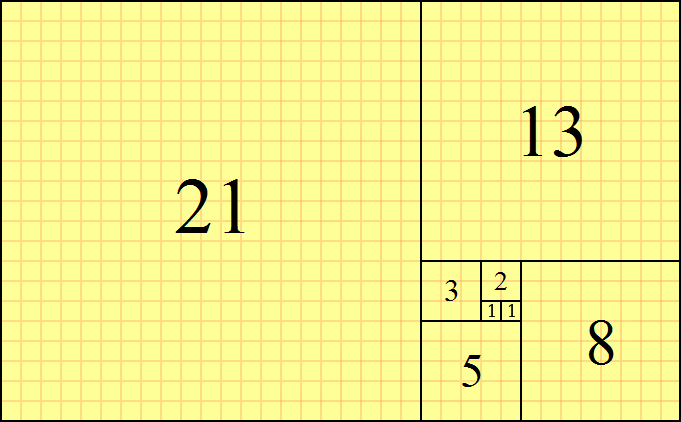
파노나치 수열에서 1번째 파보나치 수는 1, 2번째 파보나치 수는 1이고 3번째 파보나치 수는 1번째 수와 2번째 수를 더한 2와 같은 방식이 끝도 없이 이어지는데 이를 적자면 아래와 같습니다.(f는 fibo 함수)
f(1) = 1
f(2) = 1
f(3) = f(1) + f(2) = 2
f(4) = f(2) + f(3) = 3
...
f(n) = f(n - 2) + f(n - 1)
위를 점화식(점화식이란 인접한 항들 사이의 관계식을 의미)으로 표현하면 아래와 같이 표현합니다.
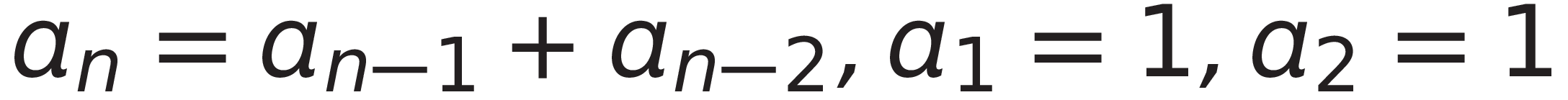
이 점화식에 따라서 피보나치함수를 재귀적으로 구현하면 다음과 같습니다.
# 피보나치 함수를 재귀 함수로 구현
def fibo(x):
# x가 1 또는 2일경우 1 반환
if x == 1 or x == 2:
return 1
return fibo(x - 1) + fibo(x - 2)
print(fibo(6))그런데 피보나치 수열의 소스코드를 이렇게 작성하면 심각한 문제가 생길 수 있습니다. fibo(x) 함수에서 x가 커지면 수행 시간이 기하 급수적으로 늘어나기 때문입니다(시간복잡도가 O(2^n)). 만약 fibo(6)을 호출한다고 가정하고 그 과정을 그림으로 그려보겠습니다.
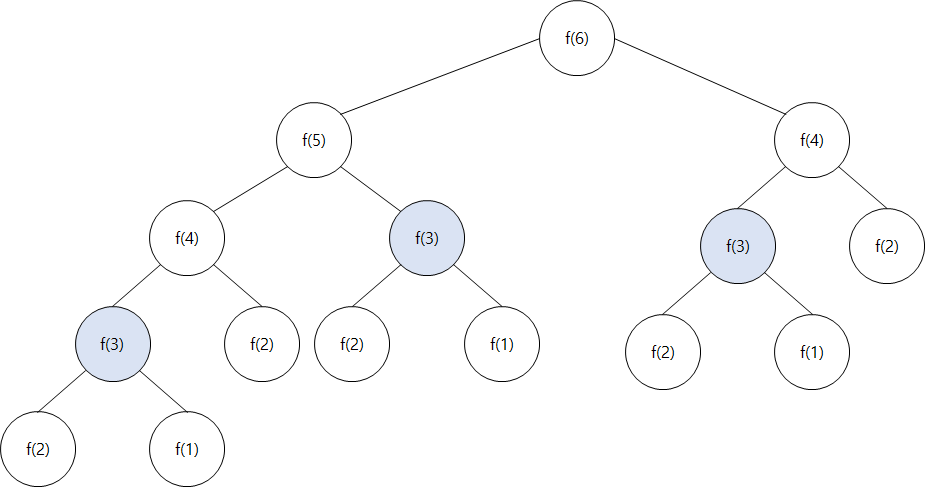
중복되는 계산이 계속해서 발생합니다. f(3)의 호출만 봐도 3번이 호출되었습니다. 만약 x가 커진다면 반복해서 호출되는 횟수가 더욱 많아집니다.
다이나믹 프로그래밍 - 그리디 알고리즘 - 분할 정복
다이나믹 프로그래밍에 대해 자세히 알아보기 전에 최적 부분 구조 라는 개념을 알아보겠습니다. 우선 위의 세 알고리즘은 모두 최적 부분 구조(Optimal Substructure)를 갖고 있는 문제입니다. 여기서 최적 부분 구조란 문제의 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 구성되는 경우 를 뜻합니다. 그림을 통해 예시를 들어보겠습니다.
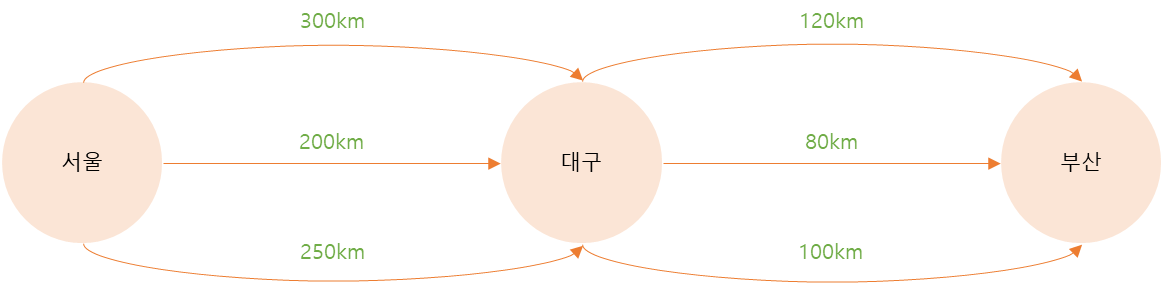
예시로 서울에서 부산까지 가는 최단 경로를 찾는 문제로 들겠습니다. 위에서 보면 서울에서 대구까지 가는 경로는 3가지가 있고, 부산까지도 마찬가지로 3가지 경로가 있습니다. 그림을 보면 알겠지만 서울에서 부산까지 가는 최단 경로는 200km + 80km 인 280km 입니다. 이 경로는 서울에서 대구까지 가는 최단 경로(200km)와 대구에서 부산까지 가는 최단 경로(80km)로 구성이 됩니다. 즉 서울에서 부산까지 가는 최단 경로는 각각의 부분 1) 서울에서 대구까지 가는 최단 경로 문제와 2) 대구에서 부산까지 가는 최단 경로 문제의 해결 방법의 합 입니다. 따라서 문제의 최적 해결 방법은 부분 문제에 대한 최적 해결 방법으로 구성이 되고, 이러한 구조를 최단 부분 구조 라고 하는 것입니다. 위에서 본 파보나치 수열 또한 최적 부분 구조 문제에 해당합니다.
만약, 위의 예시에서 서울에서 부산까지 바로 연결되는 길이 개통되어 더 이상 대구를 거칠 필요가 없다면, 이 문제는 더는 최적 부분 구조가 아닙니다.
이런 최적 부분 구조 유형의 문제는 다이나믹 프로그래밍뿐만 아니라 분할 정복 또는 그리디 알고리즘으로 접근해볼 수 있는 문제의 후보 가 됩니다. 그렇다면 "최적 부분 구조 유형의 문제가 나왔을 때 어떻게 다이나믹 프로그래밍 유형의 알고리즘 문제인지 파악하는가?" 에 대한 답변은 아래의 다이나믹 프로그래밍의 조건에서 알아보도록 하겠습니다.
다이나믹 프로그래밍 조건
- 큰 문제를 작은 문제로 나눌 수 있습니다(최적 부분 구조)
- 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일합니다
- 중복된 하위 문제들을 갖습니다
위의 조건 중 다이나믹 알고리즘으로 풀 수 있는 문제들과 다른 문제들(그리디 알고리즘, 분할 정복 등)의 결정적 차이는 중복된 하위 문제들을 갖는다는 점 입니다.
파보나치 수열은 이러한 조건을 만족하는 대표적인 문제입니다. 파보나치 수열에서 중복된 하위 문제들을 갖는다는 것은 이미 위에서 확인하였습니다. 이 부분이 핵심으로, 중복 문제가 발생하지 않는 병합 정렬은 분할 정복으로 분류되지만, 파보나치 수열을 풀이하는 알고리즘은 다이나믹 프로그래밍의 대상으로 분류되는 이유입니다.
다이나믹 프로그래밍 방법론
지금까지 최적 부분 구조와 중복된 하위 문제들로 구성된다는 다이나믹 프로그래밍의 패러다임을 살펴보았습니다. 이제는 다이나믹 프로그래밍의 방법론을 알아보도록 하겠습니다.
다이나믹 프로그래밍의 방법론은 크게 두 가지로 나뉩니다. 일반적으로 상향식을 타뷸레이션, 하향식을 메모이제이션이라고 구분해 부르기도 합니다.
- 상향식(Bottom-Up)
더 작은 하위 문제부터 살펴본 다음, 작은 문제의 정답을 이용해 큰 문제의 정답을 풀어나갑니다. 타뷸레이션(Tabulation) 이라고 부르며, 일반적으로 이 방식만을 다이나믹 프로그래밍이라고 지칭하기도 합니다.
- 하향식(Top-Down)
하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스러운 방식으로 풀어나갑니다. 이 방식을 특별히 메모이제이션(Memoization)이라 지칭합니다.
하향식(Top-Down = Memoization)
# 한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100
# 파보나치 함수를 재귀적으로 구현(탑다운 다이나믹 프로그래밍)
def fibo(x):
# 종료 조건(1 혹은 2일 때 1을 반환)
if x == 1 or x == 2:
return 1
# 이미 계산한 적 있다면 그대로 반환
if d[x] != 0:
return d[x]
# 아직 계산하지 않은 문제라면 점화식에 따라 파보나치 결과 반환
d[x] = fibo(x - 1) + fibo(x - 2)
return d[x]
print(fibo(99))하향식 방법론은 하위 문제에 대한 정답을 계산했는지 확인해가며 문제를 자연스럽게 재귀로 풀어나갑니다. 기존 재귀 풀이와 거의 동일하면서도 이미 풀어봤는지 확인하여 재활용하는 효율적인 방식으로, 메모이제이션 방식이라고 부릅니다.
상향식(Bottom-Up = Tabulation)
# 앞서 계산된 결과를 저장하기 위한 DP 테이블
dp = [0] * 100
# 첫 번째 파보나치 수와 두 번째 파보나치 수는 1
dp[1] = 1
dp[2] = 1
# 파보나치 99의 값을 알아보기 위한 수
n = 99
# 파보나치 함수 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
print(dp[n])상향식 방법론은 작은 하위 문제부터 차례대로 정답을 풀어나가며 큰 문제의 정답을 만듭니다. 데이터를 테이블 형태로 만들면서(Tabulate) 문제를 풀이한다고 하여 타뷸레이션 방식이라고 부릅니다.
두 방법의 핵심은 구한 결과를 저장해(메모해) 같은 식을 다시 호출하지 않고 저장된 결과를 반환하여 메모리의 사용량은 늘리지만 시간을 단축하는 것입니다.
정리
우선 문제가 주어지면 당연한 것이지만 다이나믹 프로그래밍 유형인지를 먼저 파악해야 합니다. 따라서 최적 부분 구조에 해당하는지 파악하고, 최적 부분 구조에 해당한다면 다이나믹 프로그래밍을 적용할 수 있는지 해결하고자 하는 부분 문제들의 중복 여부를 확인 해야합니다.
일단 단순히 재귀 함수로 프로그램을 작성한 뒤에 (탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 즉 메모이제이션을 적용할 수 있으면 코드를 개선하는 방법도 좋은 아이디어다(파보나치 수열을 재귀 함수로 구현한 뒤에 메모이제이션을 적용하는 방식과 같이).
또한 가능하다면 재귀 함수를 이용하는 탑다운 방식보다는 보텀업 방식으로 구현하는 것을 권장한다. 재귀 함수는 스택 크기가 한정되어 있을 수 있기 때문이다.
다이나믹 프로그래밍 - 그리디 알고리즘 - 분할 정복 구분
| 알고리즘 | 풀이 가능한 문제들의 특징 | 풀이 가능한 문제 및 알고리즘 |
|---|---|---|
| 다이나믹 프로그래밍 | 최적 부분 구조(Optimal Substructure) 중복된 하위 문제들(Overlapping Subproblems) | 파보나치 수열 다이나믹 프로그래밍 |
| 그리디 알고리즘 | 최적 부분 구조(Optimal Substructure) 탐욕 선택 속성(Greedy Choice Property) | 분할 가능 배낭 문제 다익스트라 알고리즘 |
| 분할 정복 | 최적 부분 구조(Optimal Substructure) | 병합 정렬 퀵 정렬 |
예제
참조
취업을 위한 코딩 테스트다 with 파이썬
파이썬 알고리즘 인터뷰
틀린 부분을 댓글로 남겨주시면 수정하겠습니다..!!