벨만 포드 알고리즘

벨만 포드 알고리즘은 다익스트라 알고리즘과 똑같이 한 정점에서 다른 모든 정점으로 가는데 걸리는 최소 비용(최단 경로)를 찾는 알고리즘 기법이다. 벨만 포드 알고리즘과 다익스트라 알고리즘의 가장 큰 차이점은 벨만 포드 알고리즘은 방향 그래프에서 음의 가중치를 지닌 간선이 존재해도 사용할 수 있다 라는 점입니다. 따라서 음의 가중치를 가진 방향 그래프를 주면서 최단 거리를 구하라고 한다면 다익스트라 알고리즘이 아닌 벨만 포드 알고리즘을 사용 해야 합니다. 우선 다익스트라 알고리즘을 사용하면 왜 음수 가중치를 가진 최단 경로를 찾을 수 없는지 확인해보겠습니다.

다익스트라 알고리즘 vs 벨만 포드 알고리즘

위와 같은 그래프가 주어진다면1번 -> 3번으로 가는 최단 경로는 직접 파악해보면 아시겠지만 1번 -> 2번 -> 3번(20 + (-15) = 5) 경로에 해당합니다. 하지만 다익스트라 알고리즘을 사용 해서 파악한다면 다익스트라 알고리즘에서는 매번 방문하지 않는 노드중에서 최단 거리가 가장 짧은 노드를 선택 하기에 1번 -> 3번(10) 경로를 선택하게 됩니다. 이처럼 음수 간선이 존재하면 다익스트라 알고리즘은 최단 거리를 찾을 수 없는 상황이 발생합니다.

벨만 포드 알고리즘 사용 예시

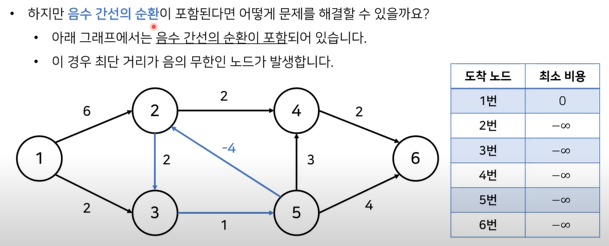
벨만 포드 알고리즘을 사용한다면 음수 가중치를 가지더라도 최단 거리를 파악할 수 있고 위의 그림과 같이 음수 간선의 순환이 발생하면 순환을 감지 할 수도 있습니다. 음수 간선의 순환이란 그림에서 2번 -> 3번 -> 5번과 같이 사이클안에 큰 음수가 포함될 때, 계속해서 반복적으로 돌면 음의 무한에 수렴하는 값을 가지는 상황입니다. 이제 과정과 코드를 통해 이를 어떻게 감지하고 최단 거리를 구하는지 알아보도록 하겠습니다.

벨만 포드 알고리즘 과정

1. 출발 노드를 설정합니다.
2. 최단 거리 테이블을 초기화합니다.
3. 다음의 과정을 V - 1 번(노드의 개수 만큼 = 모든 노드) 반복합니다.
   1. 전체 간선 E개를 하나씩 확인합니다.
   2. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신합니다.
   3. 다익스트라 알고리즘과는 다르게 모든 간선을 확인하므로 음수 가중치를 가지고 있어도 최단 거리가 계산이 가능합니다.

• 만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번의 과정을 한 번 더 수행합니다.
  * 이때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것입니다.
  

다익스트라 알고리즘과 똑같이 출발 노드를 설정하고, 최단 거리 테이블을 초기화 한 후 노드를 한번 씩 방문합니다. 다만, 노드를 방문할 때 다익스트라 알고리즘은 해당 노드에 붙어있는 간선만 확인하는데 비해 벨만 포드는 전체 간선을 방문하게 됩니다. 여기서 전체 간선을 방문하기에 음수 가중치가 포함되어 있으면 해당 가중치를 사용하여 최단 거리 테이블을 갱신할 수가 있는 것입니다.

벨만 포드 알고리즘 코드

import sys

input = sys.stdin.readline
INF = sys.maxsize

# 노드의 개수, 간선의 개수
V, E = map(int, input().split())
# 간선의 정보
edges = []

for _ in range(E):
    # 시작 노드, 도착 노드, 비용
    a, b, c = map(int, input().split())
    edges.append((a, b, c))

# 최단 거리 테이블
distance = [INF] * (V + 1)

def bf(start):
    # 시작 노드에 대해서 0으로 초기화
    distance[start] = 0

    # 전체 V - 1번의 라운드(round)를 반복
    for i in range(V):
        # 매 반복마다 "모든 간선"을 확인하며
        for j in range(E):
            cur = edges[j][0]
            next_node = edges[j][1]
            cost = edges[j][2]
            # 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if distance[cur] != INF and distance[next_node] > distance[cur] + cost:
                distance[next_node] = distance[cur] + cost

    # 음수 간선 순환 체크(한 번 더 확인해서 값이 갱신된다면 음수 순환이 존재하는 것)
    for j in range(E):
        cur = edges[j][0]
        next_node = edges[j][1]
        cost = edges[j][2]

        if distance[cur] != INF and distance[next_node] > distance[cur] + cost:
            return True

    return False

# 벨만 포드 알고리즘을 수행
negative_cycle = bf(1)

if negative_cycle:
    print("-1")
else:
    # 1번 노드를 제외한 다른 모든 노드로 가기 위한 최단 거리 출력
    for i in range(2, V + 1):
        # 도달할 수 없는 경우, -1
        if distance[i] == INF:
            print("-1")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(distance[i])

벨만 포드 알고리즘 시간복잡도

벨만 포드 알고리즘의 시간 복잡도는 O(VE)(V는 노드, E는 간선의 개수)로 다익스트라 알고리즘의 시간 복잡도 O(ElogV)보다 느리지만 음의 가중치를 가진 상황에서 사용할 수 있다는 장점이 있습니다.

요약 및 예시 문제

• 다익스트라 알고리즘

  • 매번 방문하지 않는 노드 중에서 최단 거리가 가장 짧은 노드를 선택합니다
  • 음수 간선이 없다면 최적의 해를 찾을 수 있습니다.

• 벨만 포드 알고리즘

  • 매번 모든 간선을 전부 확인합니다.
    • 따라서 다익스트라 알고리즘에서의 최적의 해를 항상 포함합니다.
  • 다익스트라 알고리즘에 비해서 시간이 오래 걸리지만 음수 간선 순환을 탐지할 수 있습니다. 즉, 음수 간선이 있어도 사용할 수 있다.

• 예시문제
  * 백준 - 타임머신

참조
코딩 테스트를 위한 벨만 포드 알고리즘 7분 핵심 요약
벨만-포드 알고리즘
알고리즘 - 벨만 포드 알고리즘
벨만포드 알고리즘 개념과 구현

틀린 부분은 댓글로 남겨주시면 수정하겠습니다..!!