[자료구조] 트리

hee09·2021년 12월 11일
자료구조
0

트리

트리의 개념

트리는 하나의 뿌리에서 위로 뻗어 나가는 형상처럼 생겨서 '트리(나무)'라는 명칭이 붙었는데, 트리 구조를 표현할 때는 나무의 형상과는 반대 방향으로 표현합니다. 트리 구조는 주변에서 쉽게 볼 수 있는 위아래 개념을 컴퓨터에서 표현한 구조로 회사의 조직도 등을 보면 보통 트리 구조 형태로 되어 있습니다.

트리의 중요한 속성 중 하나는 재귀로 정의된(Recursively Defined) 자기 참조(Self-Referential) 자료구조라는 점입니다. 쉽게 말해, 트리는 자식도 트리고 또 그 자식도 트리입니다. 흔히 서브트리로 구성된다고 표현합니다.


트리의 각 명칭

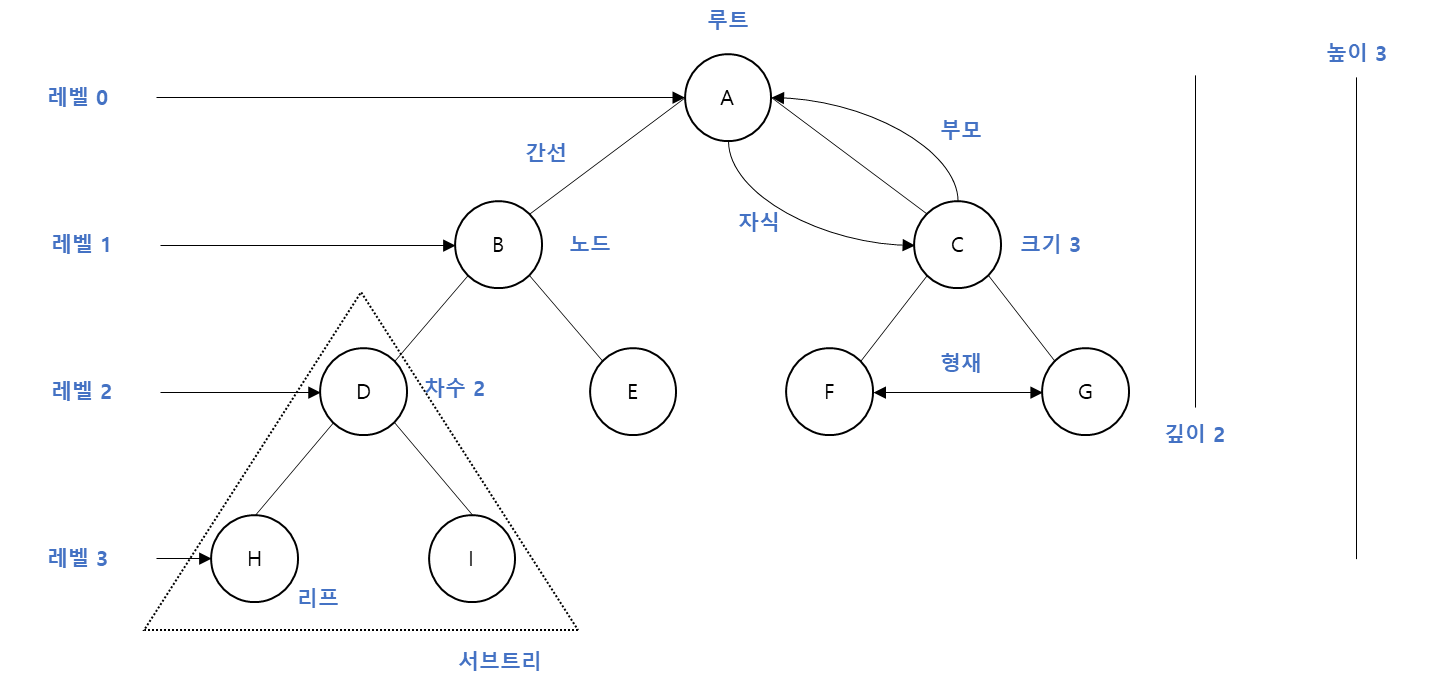
트리는 항상 루트(root)에서부터 시작합니다. 루트는 자식 노드(child)를 가지며, 간선(edge)으로 연결되어 있습니다.

  • 차수(degree) : 자식 노드의 개수

  • 크기(size) : 자신을 포함한 모든 자식 노드의 개수

  • 리프(leaf) : 자식 노드가 없는 노드

  • 높이(height) : 현재 위치에서 리프까지의 거리

  • 깊이(depth) : 루트에서부터 현재 노드까지의 거리

  • 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합

트리는 항상 단방향이기 때문에, 간선의 화살표는 생략이 가능합니다. 위의 그림에서도 생략해서 표현하였고 일반적으로 방향은 위에서 아래로 향합니다.


그래프 VS 트리

그래프와 트리의 가장 큰 차이점은 "트리는 순환 구조를 갖지 않는 그래프입니다"라는 점입니다. 핵심은 순환 구조(Cyclic)가 아니라는데 있습니다. 트리는 특수한 형태의 그래프의 일종이며 크게 그래프의 범주에 포함됩니다. 하지만 트리는 그래프와는 다르게 어떠한 경우에도 한번 연결된 노드가 다시 연결되는 법이 없습니다. 이외에도 단방향(Uni-Directional), 양방향(Bi-Directional)을 모두 가리킬 수 있는 그래포와 달리, 트리는 부모 노드에서 자식 노드를 가리키는 단방향뿐입니다. 그뿐아니라 트리는 하나의 부모 노드를 갖는다는 차이점이 있으며 루트 또한 하나여야 합니다.

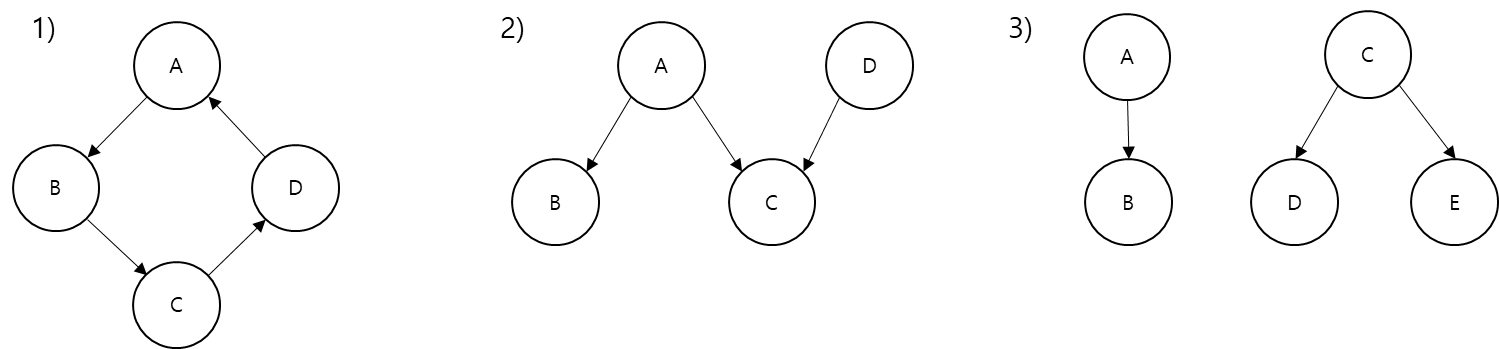
  • 1 예시
    순환 구조이기 때문에, 앞서 그래프와 트리의 차이점에서 첫 번째로 언급한, 트리는 순환 구조를 갖지 않아야 한다는 정의에 부합하지 않습니다.

  • 2 예시
    C 노드의 부모다 A, D 둘입니다. 부모 노드는 단 하나여야 합니다.

  • 3 예시
    A->B 와 D<-C->E가 서로 연결되어 있지 않으며, 루트가 둘이므로 트리가 아닙니다. 루트 또한 하나여야 합니다.


이진 트리

트리 중에서도 가장 널리 사용되는 트리 자료구조는 이진 트리와 이진 탐색 트리(Binary Search Tree = BST)입니다. 먼저, 각 노드가 m개 이하의 자식을 갖고 있으면 m-ary 트리(다항 트리, 다진 트리)라고 합니다. 여기서 m=2일 경우, 즉 모든 노드의 차수가 2 이하일 때는 특별히 이진 트리(Binary Tree)라고 부릅니다. 이진 트리는 왼쪽, 오른쪽, 최대 2개의 자식을 갖는 형태입니다. 대체로 트리라고 하면 특별한 경우가 아니고서는 대부분 이진 트리를 일컫습니다.

이진 트리의 형태

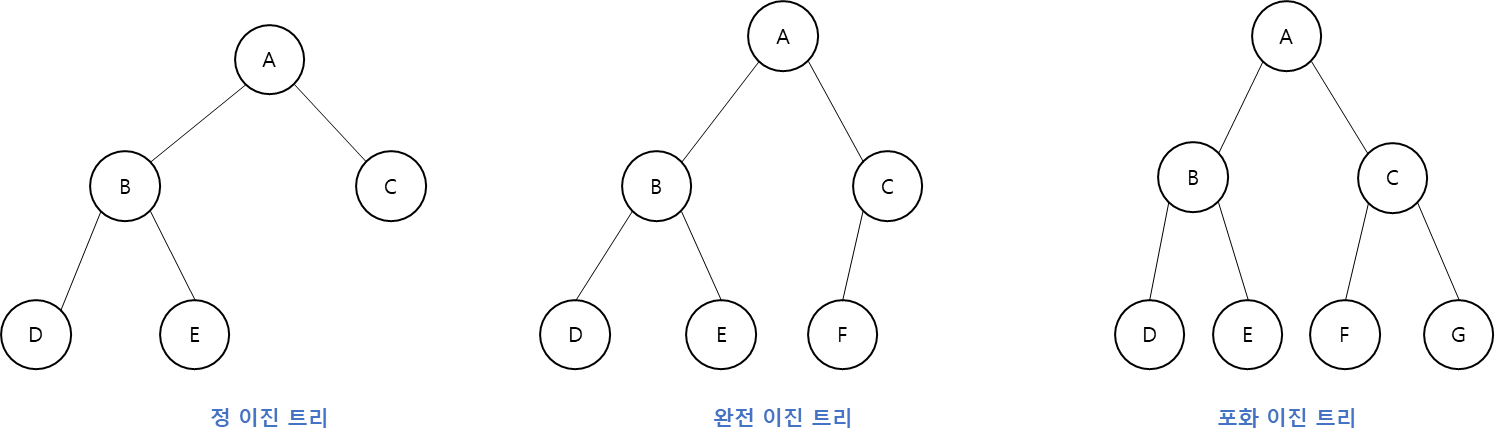
  • 정 이진 트리(Full Binary Tree): 모든 노드가 0개 또는 2개의 자식 노드를 갖습니다.

  • 완전 이진 트리(Complete Binary Tree): 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있습니다.

  • 포화 이진 트리(Perfect Binary Tree): 모든 노드가 2개의 자식 노드를 갖고 있으며, 모든 리프 노드가 동일한 깊이 또는 레벨을 갖습니다. 문자 그대로, 가장 완벽한(Perfect) 유형의 트리입니다.


이진 탐색 트리(BST)

이진 트리는 정렬 여부와 관계 없이 모든 노드가 둘 이하의 자식을 갖는 단순한 트리 형태입니다. 이진 '탐색' 트리는 정렬된 트리를 말하는데, 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이뤄져 있는 반면, 노드의 오른쪽 서브트리에는 그 노드의 값과 같거나 큰 값들을 지닌 노드들로 이루어져 있는 트리를 뜻합니다. 이렇게 왼쪽과 오른쪽의 값들이 각각 값의 크기에 따라 정렬되어 있는 트리를 이진 탐색 트리라 합니다. 이진 탐색 트리의 가장 훌륭한 점은 탐색 시 시간 복잡도가 O(lonN) 이라는 점입니다.

이진 탐색 트리에서 값 찾는 방식

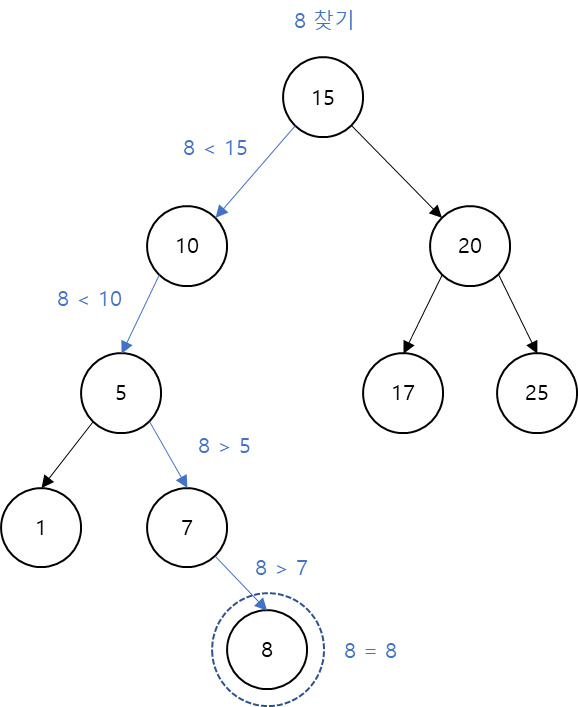
위 그림에서 과정은 아래와 같습니다.

  1. 루트는 15이며, 8은 15보다 작습니다. 따라서 왼쪽 자식 노드를 탐색합니다.

  2. 10 또한 마찬가지로 8보다 크므로, 왼쪽을 택합니다.

  3. 5는 8보다 작으므로, 오른쪽으로 탐색합니다.

  4. 그 다음, 7은 8보다 작으므로 마지막으로 오른쪽을 탐색해 정답 8을 찾을 수 있습니다.

이처럼 4번 만에 정답을 찾을 수 있습니다.

만약 여기서 정답이 없는 6을 찾는다면 5 이후에 오른쪽을 탐색하게 될 것이고, 그 다음에는 7 이후에 다시 왼쪽을 탐색하려 하는데, 더 이상 왼쪽 노드가 없으므로 탐색을 중단하게 됩니다.

균형이 깨진 이진 탐색 트리

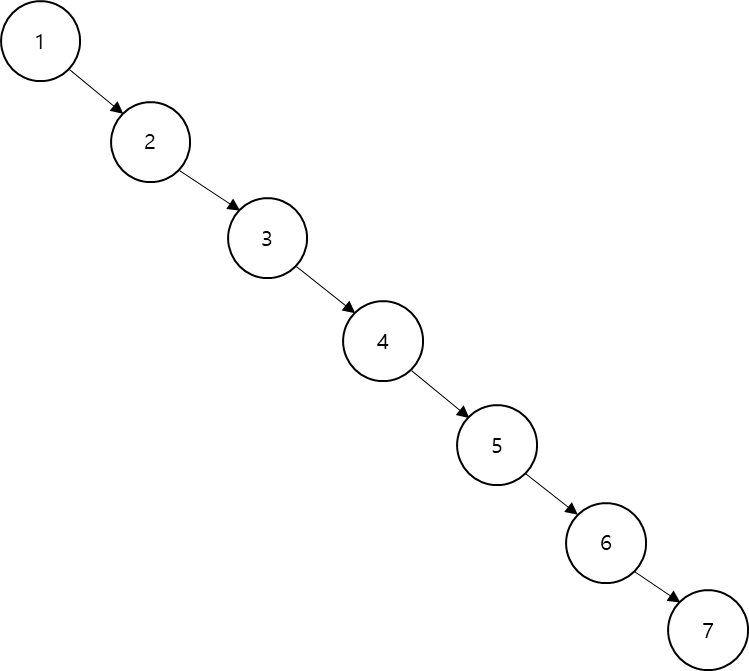
만약 랜덤하게 이진 탐색 트리를 생성하게 될 때 운이 나쁘면 위와 같이 트리의 모양이 균형을 제대로 이루지 못할 수 있습니다. 균형이 많이 깨지면 탐색 시에 O(logN)이 아니라 O(N)에 근접한 시간이 소요될 수 있습니다.

이와 같이 비효율적으로 구성이 되면 연결 리스트와 다를 바가 없습니다. 7을 찾기 위해서는 루트부터 맨 끝까지 차례대로 모두 탐색해야 하므로 전혀 효율적이지 않습니다. 강력한 로그 계산을 기반으로 하는 이진 탐색 트리의 장점을 전혀 살릴 수 없습니다. 따라서 이런 트리는 균형을 맞춰 줄 필요가 있는데, 그래서 고안해낸 것이 '자가 균형 이진 탐색 트리'입니다.


자가 균형 이진 탐색 트리

자가 균형(또는 높이 균형) 이진 탐색 트리는 삽입, 삭제 시 자동으로 높이를 작게 유지하는 노드 기반의 이진 탐색 트리입니다. 자가 균형 이진 탐색 트리(Self-Balancing Binary Tree)는 최악의 경우에도 이진 트리의 균형을 잘 맞도록 유지합니다. 즉 높이가 가능한 한 낮게 유지하는 것이 중요하다는 이야기입니다.


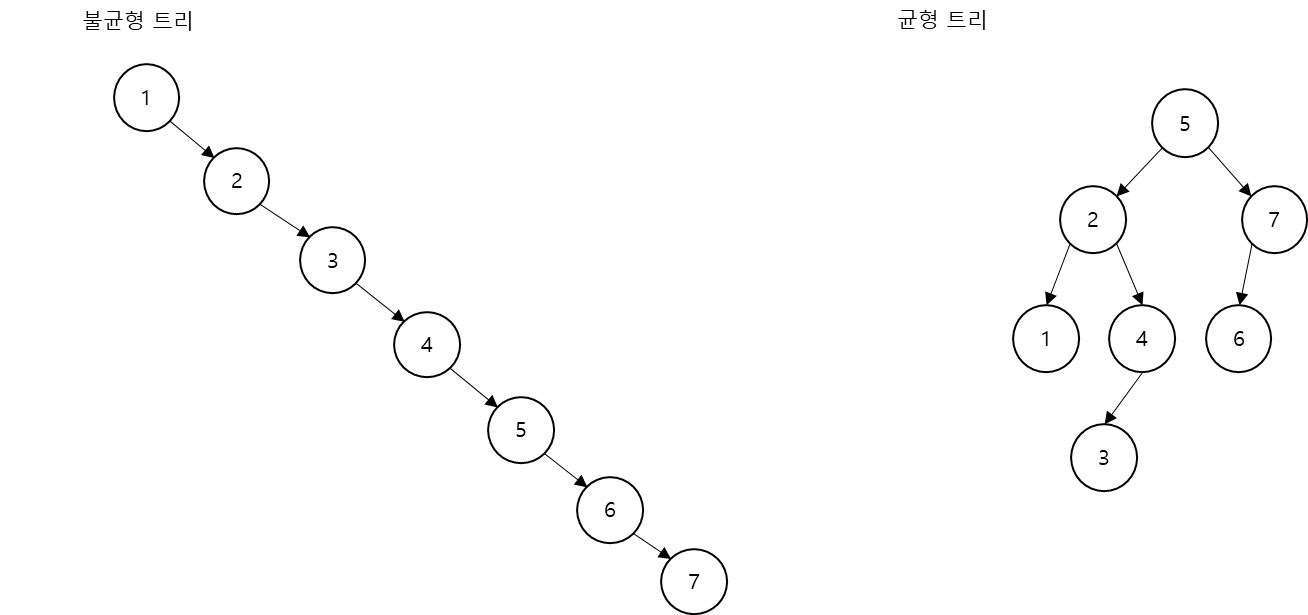
균형이 잘 잡힌 트리는 루트의 높이가 3으로, 높이를 가능한 한 작게 유지한 트리임을 확인할 수 있습니다. 균형이 맞지 않는 불균형 트리는 루트의 높이가 6으로 매우 높습니다.

위의 그림에서 원하는 값을 찾으려면 불균형 트리에서는 7을 찾기 위해 7번의 연산이 실행되어야 합니다. 그러나 균형 잡힌 트리는 불과 두 번 만에 7을 찾는게 가능합니다. 만약 노드가 100만개라고 가정하면 불균형 트리는 100만번의 연산이 필요하고 균형 잡힌 트리는 균형이 완벽히 잡혀 있다고 가정할 때 최대 19번이면 어떤 값이든 반드시 찾아내는 게 가능합니다.

이처럼 불균형과 균형의 성능 차이는 큽니다. 따라서 균형, 즉 높이의 균형을 맞추는 작업은 매우 중요합니다. 이와 같이 높이 균형을 맞춰주는 자가 균형 이진 탐색 트리의 대표적인 형태로는 AVL 트리와 레드-블랙 트리 등이 있으며, 특히 레드-블랙 트리는 높은 효율성으로 인해 실무에서도 매우 빈번하게 쓰이는 트리 형태입니다. 자바의 해시맵 또한 효율적인 저장 구조를 위해 해시 테이블의 개별 체이닝(Seperate Chaining) 시 연결리스트와 함께 레드-블랙 트리를 병행해 저장하는 구조로 구현되어 있습니다.


트리 순회

트리 순회란 그래프 순회의 한 형태로 트리 자료 구조에서 각 노드를 정확히 한 번 방문하는 과정을 말합니다. 그래프 순회와 마찬가지로 트리 순회(Tree Traversals) 또한 DFS 또는 BFS로 탐색하는데, 특히 이진 트리에서 DFS는 노드의 방문 순서에 따라 다음과 같이 크게 3가지 방식으로 구분됩니다.

  • 전위(Pre-Order) 순회(NLR)
    현재 노드를 순회한 다음 왼쪽과 오른쪽 서브트리를 순회

  • 중위(In-Order) 순회(LNR)
    왼쪽 서브트리를 순회한 다음 현재 노드와 오른쪽 서브 트리를 순회

  • 후위(Post-Order) 순회(LRN)
    왼쪽과 오른쪽 서브트리를 순회한 다음 현재 노드를 순회

순회 방식의 영문 문자어를 구성하는 3가지 문자 L,R,N 중 L은 현재 노드의 왼쪽 서브트리, R은 현재 노드의 오른쪽 서브트리, N은 현재 자신의 노드를 의미합니다.

트리 순회 예시

직접 트리를 그리고 순회 방식에 따른 순서를 나열해보겠습니다.

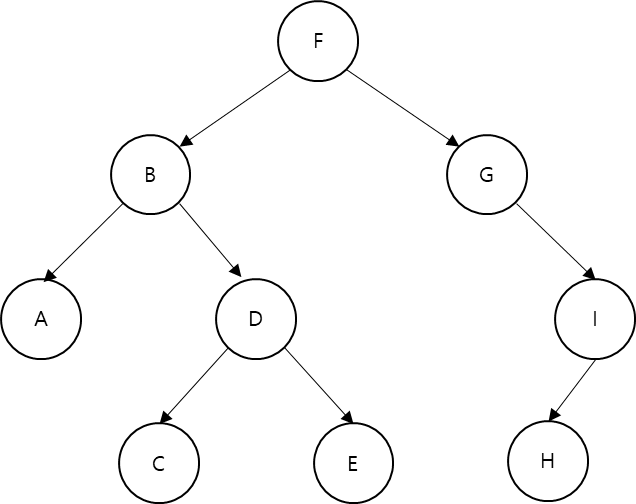
  • 전위(NLR): F, B, A, D, C, E, G, I, H
  • 중위(LNR): A, B, C, D, E, F, G, H, I
  • 후위(LRN): A, C, E, D, B, H, I, G, F

트리 순회 코드

트리는 앞서 언급한 대로 재귀적인 특성을 가지고 있습니다. 따라서 재귀 구현이 훨씬 더 간단하고 직관적이기에 재귀로 구현하는 코드를 작성하겠습니다.

우선 연결리스트를 담을 Node 클래스를 정의하고 트리의 전체 입력값을 root 변수로 아래와 같이 정의하겠습니다. root에 담긴 트리는 위에 나온 그림과 같은 트리입니다.

class Node:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

root = Node('F',
            Node('B',
                Node('A'),
                Node('D',
                    Node('C'), Node('E')),
                ),
            Node('G',
                None,
                Node('I', Node('H'))
                )
            )

아래는 각 순회에 대한 코드와 그 결과입니다.

  • 전위 순회(NLR)
# 전위 순회
def preorder(node):
    if node is None:
        return
    
    # 자기 자신 방문
    print(node.val, end=" ")
    # 왼쪽 방문
    preorder(node.left)
    # 오른쪽 방문
    preorder(node.right)
    
preorder(root)

결과 : F, B, A, D, C, E, G, I, H

  • 중위 순회(LNR)
# 중위 순회
def inorder(node):
    if node is None:
        return
    
    # 왼쪽 방문
    inorder(node.left)
    # 자기 자신 방문
    print(node.val, end=" ")
    # 오른쪽 방문
    inorder(node.right)

inorder(root)

결과 : A, B, C, D, E, F, G, H, I

  • 후위 순회(LRN)
# 후위 순회
def postorder(node):
    if node is None:
        return

    # 왼쪽 방문
    postorder(node.left)
    # 오른쪽 방문
    postorder(node.right)
    # 자기 자신 방문
    print(node.val, end=" ")

postorder(root)

결과 : A, C, E, D, B, H, I, G, F

참고
파이썬 알고리즘 인터뷰

틀린 부분 댓글로 남겨주시면 수정하겠습니다..!!

profile
hee09
되새기기 위해 기록
이전 포스트

[안드로이드] CardView

다음 포스트

[코틀린] 널 가능성

0개의 댓글