
기초부터 쌓아가는 머신러닝 #6
6주차 : Decision Tree 이론 및 실습
Decision Tree란 무엇인가?
- 의사결정 규칙을 나무 구조로 나타내어 전체 자료를 몇 개의 작은 집단으로 나누어서 분석하는 기법이다.
- SVM 처럼 결정트리(decision tree)는 분류 및 회귀가 가능한 머신러닝 알고리즘이다.
- 매우 복잡한 데이터셋도 학습할 수 있는 강력한 알고리즘
- 최근에 많이 사용하는 랜덤 포레스트의 기본 구성 요소이다.
Decision Tree 학습과 시각화
- 결정 트리의 이해를 돕기 위해서, 지난 시간에 배운 iris예제를 가지고 모델을 학습시켜서 시각화 해보겠다.
from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier from sklearn.tree import export_graphviz from subprocess import check_call iris = load_iris() x = iris.data[:,2:] # 꽃잎의 길이, 너비 y = iris.target # decision tree 모형 인스턴스 생성 및 하이퍼파라미터(depth) = 3 tree_model = DecisionTreeClassifier(max_depth=3) tree_model.fit(x,y) export_graphviz( tree_model, # 학습한 모형 out_file = './iris_tree_model.dot', # .dot 파일 저장 위치 feature_names = iris.feature_names[2:], # 사용한 변수 이름 class_names = iris.target_names, # 예측할 타겟 클래스 이름 rounded=True, # 사각형 끝을 둥글게 filled=True # 사각형 안 색깔 채우기 ) # 예측한 모형 png로 바꿔서, 시각화 하기 check_call(['dot','-Tpng','iris_tree_model.dot','-o','OutputFile.png'])
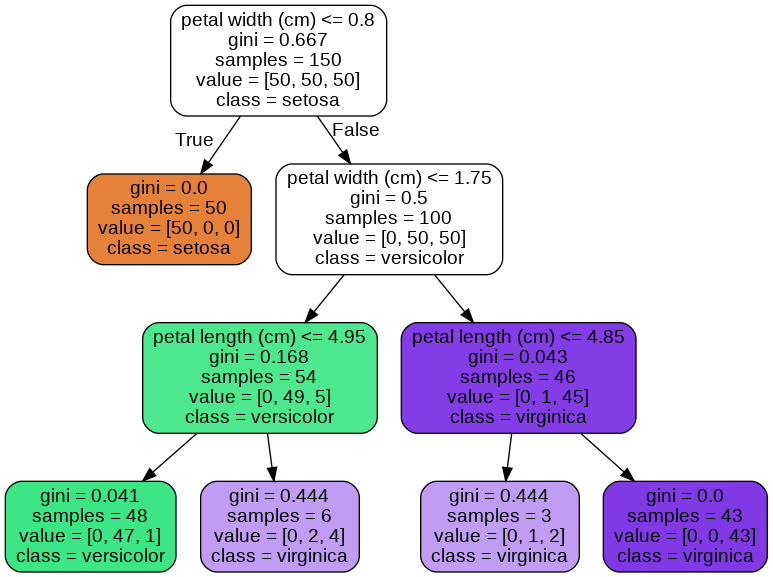
Decision Tree 예측하기
⛑ 용어 정리
- Root Node(루트 노드) : 깊이가 0인 꼭대기 노드
- Leaf Node(리프 노드) : 자식 노드가 없는 마지막 노드
- Gini Impurity(지니 불순도) : 한 노드의 모든 샘플이 같은 클래스에 속해있으면, 해당 노드는 순수(gini=0)하다고 한다.
- 첫번째로 root node(꼭대기)에서 시작한다.
- petal width가 0.8과 같거나 작은지 검사한다.(조건에 따라 좌우 분기)
- 만약 False라면 오른쪽으로 이동해 root node에서 했던 조건 검사를 실시하여 반복하여 분기한다.
- 마지막에 leaf node(끝)에 도달했을 때, 추가적인 조건 검사 없이 가장 많은 클래스의 비중을 차지하고 있는 곳으로 클래스를 예측하게 된다.
- 결정 트리의 장점 : 스케일이나 평균을 원점에 맞추는 것과 같은 데이터 전처리가 거의 필요하지 않다.
- 사이킷런은 이진 트리(자식 노드의 수가 2개 이하)만 만드는 CART 알고리즘을 사용한다.
- 결정 트리는 위와 같이 매우 직관적이고 이해하기 쉽고, 해석력이 아주 좋다. (이러한 모델을 '화이트 박스'라고 부른다')
- 반대로 다음 시간에 할 랜덤 포레스트와 신경망은 '블랙 박스'인데, 성능은 뛰어나지만 해석력이 떨어집니다.
- 그래서 상황(데이터 종류, 모델 적용할 비즈니스 모델, 환경 등등)을 고려해서 모델선택을 하여야 한다.
Decision Tree 클래스 확률 추정
- 결정 트리도 한 샘플이 특정 클래스에 속할 확률을 추정토록 할 수 있다.
- 위 과정처럼 어떤 샘플이 각 조건에 따라서 리프 노드로 분기를 하고, 해당 노드에 클래스 비율이 곧 클래스 확률이 된다.
tree_model.predict_proba([[3.1,2]]) >array([[0. , 0.33333333, 0.66666667]]) # 인덱스 2번이 가장 높은 0.6666667이라는 확률값을 산출하여 2번 클래스를 예측한다. tree_model.predict([[3.1,2]]) >array([2])
CART 훈련 알고리즘
-
위에서 말한대로 사이킷런의 결정트리 훈련 방식은 CART(Classification And Regression Tree) 알고리즘을 사용한다.
-
CART 알고리즘 아이디어
1.훈련 세트 중 하나의 특성과 거기에 대한 임계값을 정한다. ex) "Petal width < 2.6"
2.특성과 임계값을 고를 때는 가장 순수한(pure) 서브셋으로 나눌 수 있는 짝을 찾는다.
3.비용함수(loss function)은 다음과 같다.

4.훈련 세트를 순수하게 잘 나눴다면 위 방식을 반복적으로 지정한 max_depth만큼 서브셋으로 나눈다. -
CART 알고리즘은 root node에서부터 최적의 분기를 찾으면서 최대한 불순도를 낮추려고 하는 greedy algorithm(탐욕적 알고리즘)이다.
다르게 말하면, 미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법이다. 이렇게 각 단계에서 최선의 선택을 한 것이 전체적으로도 최선이길 바라는 알고리즘, 하지만 종종 충분히 훌륭한 모델을 찾곤 한다.
계산 복잡도
- decision tree를 학습시키기 위해서는 root node ~ leaf node까지 탐색을 해야 한다.
- 일반적으로 결정 트리는 평행하게 가지 분기를 하기 때문에, 모든 결정트리를 탐색하기 위해서는 약 log(m)/log(2) 만큼의 노드를 거쳐야한다.
- 각 노드의 한 개의 특성값만 확인하기 때문에, 예측에 필요한 전체 복잡도는 특성 수와 무관하게 log(m)/log(2)이다.
- 곧, 훈련 세트가 매우 클 경우에도 예측 속도가 아주 빠르다는 것을 알 수 있다.
- 그러나.. 훈련 알고리즘의 경우에는 각 노드에서 모든 훈련 샘플의 모든(max feature 이하) 특성을 비교한다.
- 그래서 훈련 복잡도는 n X m X log(m)이 된다.
- 그리고 훈련 세트가 (수천개 이하)만큼 작은 경우에는 DecisionTreeClassifier(~~~, presort = True)를 하게 되면 미리 데이터를 정렬하여 훈련 속도를 높일 수 있다.
presort : (기본값 = False) 피팅에서 최상의 분할을 찾는 속도를 높이기 위해 데이터를 사전 정렬할지 여부이다. 대규모 데이터 세트에 대한 의사 결정 트리의 기본 설정의 경우이를 true로 설정하면 훈련 프로세스가 느려질 수 있지만, 더 작은 데이터 세트 또는 제한된 깊이를 사용하면 훈련 속도가 빨라질 수 있습니다.
지니 불순도 또는 엔트로피
- Decision Tree Classifier의 criterion : 기본값 "gini"이고, Decision Tree Regressor의 criterion : 기본값 "mse" 를 사용한다.
- 만약에 criterion 매겨변수를 열역학 개념에서 많이 사용하는 "entropy"로 지정하여 엔트로피 불순도를 사용할 수 있다. -> 머신러닝의 불순도 측정 방법으로 많이 사용된다.
- 만약, 한 노드가 한 클래스의 샘플만 가지고 있다면 엔트로피 역시 "0" 이 된다.
- " 그렇다면 지니 불순도와 엔트로피 중 어떤 것을 사용해야 하나? " 답은 실제로 차이가 별로 없다이다.
- 지니 불순도의 경우가 약간 계산이 빠르다는 이유로 default값으로 많이 사용된다.
- 하지만 지니 불순도의 경우에는 빈도가 높은 클래스를 한쪽 가지로 고립시키는 경향이 있고, 엔트로피의 경우에는 조금 더 평형을 유지 하는 트리를 만드는 경향을 보인다.
규제 매개변수
- 결정 트리의 경우 훈련 데이터에 대한 가정을 보통 두지 않는다. (<=>선형 모델의 경우에는 데이터가 선형일거라 가정)
- 하지만 훈련 데이터에 대한 일반적인 가정을 두지 않는다면, 모델 자체가 훈련 데이터와 아주 가깝게 만들려고 해서 과접합이 발생할 수 있다.
- 결정 트리 모델의 경우에는 일반적인 선형 모델과 같이 파라미터 모델이 아니다.
- 결정 트리 모델은 훈련되기 전에 파라미터의 수를 지정할 수 없는 비파라미터 모델(nonparametric model)이다.
- 비파라미터 모델은 훈련 데이터에 맞춰지기 때문에 모델 구조가 고정되지 않고 자유롭다.
- 파라미터 모델은 미리 파라미터를 정할 수 있기 때문에 제한적이지만 과대적합의 위험을 조절할 수 있다.
- 결정 트리는 보통 최대 깊이(max_depth)로 모델의 과적합을 규제할 수 있다.
- max_depth가 낮아지면 과대적합의 위험이 감소될 수 있다.
- 결정 트리의 규제 매개변수 종류
-
max_depth : 트리 최대 깊이
- max_depth 감소 => 모델 규제 증가 => 과적합 감소
-
min_samples_split : 분할되기 위해 노드가 가져야 하는 최소 샘플 수
- min_samples_split 증가 => 모델 규제 증가 => 과적합 감소
-
min_samples_leaf : leaf node가 가지고 있어야할 최소 샘플 수
- min_samples_leaf 증가 => 모델 규제 증가 => 과적합 감소
-
min_weight_fraction_leaf : min_samples_leaf와 비슷하지만, 가중치가 부여된 전체 샘플 수에서의 비율
- min_weight_fraction_leaf 증가 => 모델 규제 증가 => 과적합 감소
-
max_leaf_nodes : leaf node의 총 최대 개수
- max_leaf_nodes 감소 => 모델 규제 증가 => 과적합 감소
-
max_features : 최상의 분할을 찾을 때 고려할 기능의 수
- max_features 감소 => 모델 규제 증가 => 과적합 감소
TIP : min_으로 시작하는 매개변수 증가 => 모델 규제 증가 => 과적합 감소
TIP : max_으로 시작하는 매개변수 감소 => 모델 규제 증가 => 과적합 감소
Decision Tree를 활용한 회귀
- decision tree(결정 트리)를 활용하여 회귀문제 또한 해결할 수 있다.
from sklearn.tree import DecisionTreeRegressor # max_depth = 3 tree_model = DecisionTreeRegressor(max_depth=3) tree_model.fit(x,y) export_graphviz( tree_model, # 학습한 모형 out_file = './iris_tree_model_reg.dot', # .dot 파일 저장 위치 feature_names = iris.feature_names[2:], # 사용한 변수 이름 rounded=True, # 사각형 끝을 둥글게 filled=True # 사각형 안 색깔 채우기 ) # 예측한 모형 png로 바꿔서, 시각화 하기 check_call(['dot','-Tpng','iris_tree_model_reg.dot','-o','OutputFile_reg.png'])
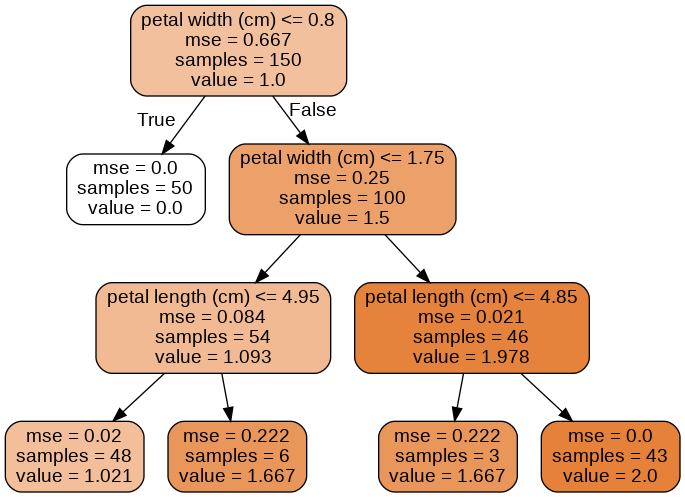
- 앞에서 classification 했을 때와 거의 비슷한 형태의 그림을 가지게 된다.
- 차이점이라고는 클래스를 예측하는 것이 아니라, 특정 연속적인 value값을 예측한다는 것이다.

- classification에서 CART알고리즘은 훈련 세트의 불순도를 줄이는 방향으로 학습하지만, 회귀에서는 형태는 비슷하게 불순도 대신 MSE를 기본값으로 사용한다.
Decision Tree의 불안정성
-
Decision Tree(결정 트리)는 이해 및 해석이 용이하면서 예측속도가 아주 빠르고 성능도 좋다.
-
하지만 결정트리는 계단 모양의 Decision Boundary(결정 경계)를 만들기 때문에 훈련 세트의 회전에 아주 민감하다.
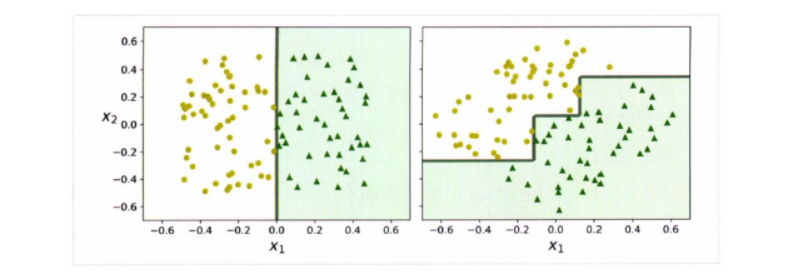
-
왼쪽의 그림의 경우에는 결정트리로 쉽게 classification을 할 수 있다.
-
하지만 왼쪽의 그림을 오른쪽 그림처럼 회전을 시키게 된다면, 결정트리는 복잡하게 형성이 된다.
-
만약 오른쪽의 그림을 새로운 데이터로 예측한다면 일반화되기란 어려울 것이다.
-
그래서 위와 같은 문제를 해결하기 위해서, PCA(Principal Component Analysis)방법을 사용할 수 있다.
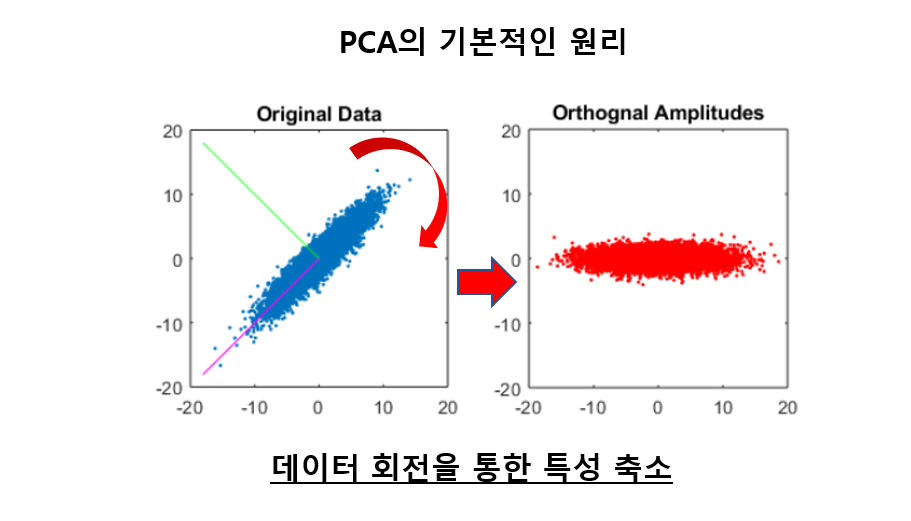
다음장에서 볼 랜덤 포레스트는 많은 트리의 예측들을 평균내어서 위에서 언급한 불안정성들을 어느정도 극복할 수 있다.
