[Python] 선형 분류 이론 및 실습

거친코딩·2021년 5월 5일

Kernel Logistic Regression SVM python 핸즈온머신러닝

기초부터 쌓아가는 머신러닝

목록 보기

6/9

기초부터 쌓아가는 머신러닝 #5

5주차 : 선형 분류 이론 및 실습

YouTube Channel(거친코딩)

- 로지스틱 회귀란 무엇인가

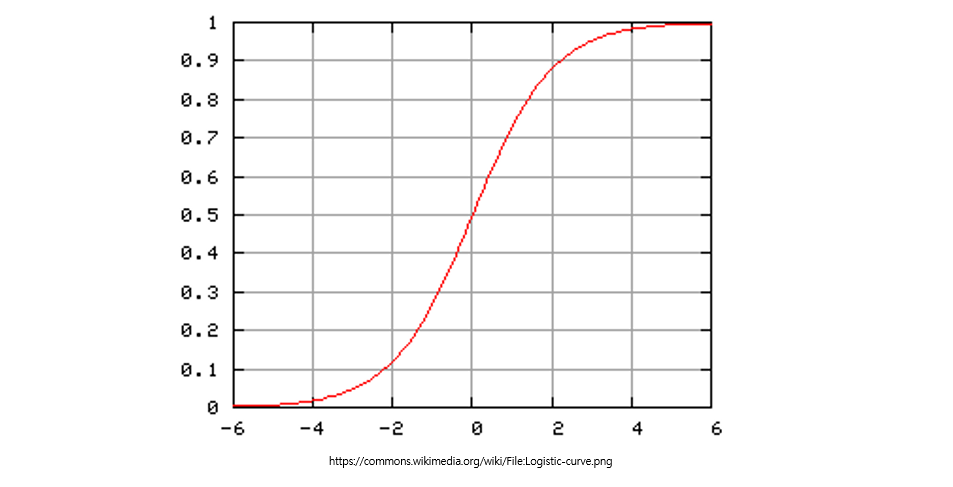
로지스틱 회귀
- 로지스틱 회귀란 샘플이 특정 클래스에 속할 확률을 추정하는 것, ex)특정 이메일이 스팸일 확률
- binary한 문제일 경우, 추정 확률이 50%가 넘으면 모델은 그 샘플이 해당 클래스에 속한다고 할 수 있음(이진 분류기)
확률을 추정하는 법
- 선형 회귀 모델과 같이 로지스틱 회귀 모델도 마찬가지로 입력 변수의 가중치 합을 계산한다.
- 대신 선형회귀와 같이 결과물을 연속적인 형태로 출력하는 것이 아니라, 0~1사이의 확률 값을 출력한다.
로지스틱 함수

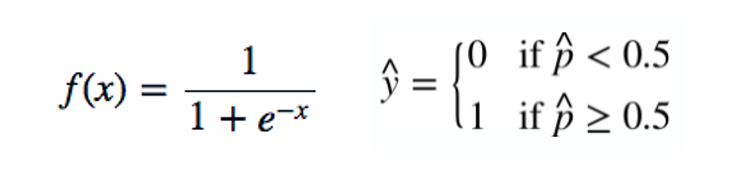
- f(x)값의 산출물인 p(probability)< 0.5 인 경우, y = 0
- f(x)값의 산출물인 p(probability)>= 0.5 인 경우, y = 1

- 로지스틱 회귀 모델의 훈련과 비용함수

로지스틱 회귀 모델의 훈련 목적은 positive(y=1)에 대한 샘플에 대해서는 높은 확률로 추정토록 하고, negative(y=0)에 대한 샘플에 대해서는 낮은 확률로 추정하게 하는 모델 최적의 가중치를 찾는 것입니다.

- (1) 비용함수는 p가 0에 가까워지면 질수록 -log값이 매우 커지고, 1에 가까워지면 질수록 0에 가까워지게 된다.
- 그래서 (1)의 경우 positive한 샘플에 대해서는 최대한 p를 1에 가깝게 만들고, negative한 샘플에 대해서는 최대한 p를 0에 가깝게 만들어야 한다.
- (2) 전체 훈련 세트에 대한 비용 함수는 (1)방식을 차용한 방식으로 모든 훈련 샘플의 비용에 평균을 한 것이다. => 이를 로그 손실이라 부른다.
- (2)의 비용 함수는 볼록 함수이므로 경사 하강법 혹은 다른 최적화 알고리즘을 통해서 전역 최소값을 찾을 수 있다.
- 그래서 만약 경사하강법을 사용하여서 모델을 최적화시킨다면 비용함수를 편미분하여서 얻어낸 그래디언트값을 통해서 가중치를 최신화 시킬 수 있다.

- 결정 경계

로지스틱 회귀를 더욱 이해하기 쉽게 설명하기 위해서 붗꽃 데이터 사용
이 데이터는 세 개의 품종 (Setosa, Versicolor, Virginica), 150개의 데이터 수, Petal(꽃잎) Sepal(꽃받침)의 너비와 길이를 가진다.

from sklearn import datasets
iris = datasets.load_iris() # sklearn의 빌트인 iris 예제 로드
print(list(iris.keys())) # iris데이터 key 값
> ['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']

x = iris['data'][:,3:] # 꽃잎의 너비 변수만 사용하겠다.
y = (iris['target']==2).astype('int') # index=2 : Versinica

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(x,y)

import numpy as np
import matplotlib.pyplot as plt
x_new = np.linspace(0,3,1000).reshape(-1,1)
# predict VS predict_proba => predict: 예측 라벨값 산출, predict_proba: 예측 확률 값 산출
y_proba = log_reg.predict_proba(x_new) 
plt.plot(x_new, y_proba[:,1], "r-", label = "Iris-Virginica")
plt.plot(x_new, y_proba[:,0], "b--", label = "not Iris-Virginica")
plt.legend()
plt.show()

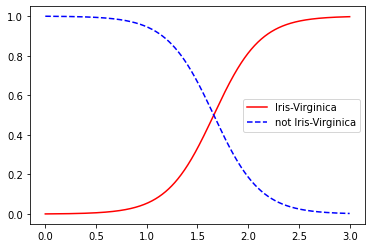
- iris의 verginica의 꽃잎 너비는 위 그림에 따르면 1.4~2.5 사이에 분포한다.
- 반면에 다른 붗꽃은 일반적으로 꽃잎 너비가 더 작아 0.1~1.8에 분포한다.
- 이렇게 약간의 겹치는 부분이 있어, 겹치는 부분의 확률 값은 극단적인 너비 값보다 작게 나타난다.

- 소프트맥스 회귀

- 로지스틱 회귀 모델은 이진 분류뿐만 아니라, 여러 클래스를 분류할 수도 있다.
- 이를 지원하는 것이 Softmax Regression(소프트맥스 회귀) 또는 다항 로지스틱 회귀라고 한다.
- (1)의 식은 각 클래스 별 softmax에 대한 점수이다.
- (2)은 각 클래스 점수를 exponential의 sum으로 나눈 것으로 정의 된다.

- (1)에서 처럼 softmax를 통해서 나온 각 클래스별 추정 확률 값이 가장 높은 클래스를 실제 클래스라고 예측한다.
- 모델의 훈련 방법은 로지스틱 회귀의 훈련 방식과 비슷하게 (2)과 같이 나타나게 되고, 이를 크로스 엔트로피라고 부른다.
- 크로스엔트로피는 추정된 클래스의 확률이 목표 클래스에 얼마나 잘 들어맞는지 판단하는 용도로 종종 사용된다.

x = iris['data'][:,(2,3)] # 꽃잎의 길이, 너비 변수 사용
y = iris['target'] # 3개 클래스 모두 사용

# multi class 역시 sklearn의 logisticregression 사용
# multi_class = 'multinomial' 옵션으로 소프트맥트 회귀를 사용할 수 있음
# solver = 'lbfgs'의 lbfgs는 의사 뉴턴 메서드 중, 제한된 메모리 공간에서 구현한 것으로 머신러닝 분야에서 많이 사용 됨
# 하이퍼파라미터 C를 통해, 이전 장에서 배운 L2 규제를 사용하게 됨
softmax_reg = LogisticRegression(multi_class='multinomial',solver='lbfgs',C=10,random_state=2021)
softmax_reg.fit(x,y)

# 꽃잎 길이 5cm, 너비 2cm의 iris 데이터를 예측한다고 가정
new_iris = [[5,2]]
prediction = softmax_reg.predict(new_iris)[0]
label = iris['target_names'].tolist()
print(label[prediction])
> virginica
softmax_reg.predict_proba(new_iris)
> array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])

- 서포트 벡터 머신이란 무엇인가

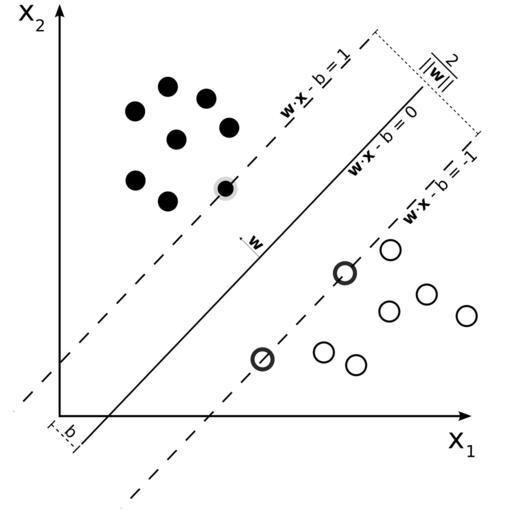
- 서포트 벡터 머신의 분류

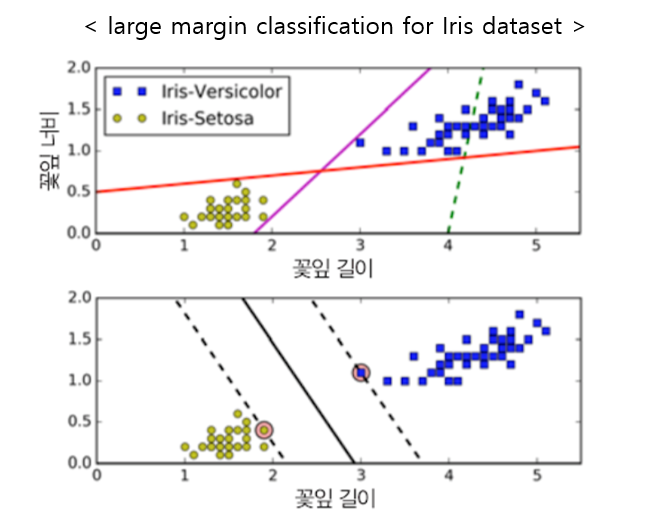
위 그림의 iris 데이터셋을 보면 SVM을 더 잘 이해하기 쉬울 것이다.
첫 번째 그림의 실선은 두 개의 클래스를 잘 분류하지 못하고 있다.
첫 번째 그림의 다른 두 모델 분류기는 정확히 분류는 하고 있으나, 모델 분류기의 선이 훈련 데이터와 너무 가까워서, 만약 새로운 new 데이터가 온다면 정확히 분류하지 못할 수도 있다.
두 번째 그림은 SVM 분류기의 결정 경계이다.
이 직선은 두 개의 클래스를 나누고 있을 뿐만 아니라, 클래스를 나누는 결정경계가 훈련샘플로부터 최대한 멀리 떨어져 있다.
그래서 SVM 분류기는 클래스 사이의 가장 폭이 넓은 구간을 찾는 것으로 이해할 수 있다. 그리고 이를 large margin classification(라지 마진 분류)라고 부른다.
방금 말한 SVM의 목적 때문에, 마진 구간 바깥쪽의 데이터는 결정 경계에 전혀 영향을 주지 않고, 오로지 마진 구간 근처에 위치한 샘플에만 결정경계는 영향을 받게 된다.
그리고 이렇게 영향을 주는 샘플들을 Support Vector(서포트 벡터)라고 부른다.
SVM 개요에서 말한 것처럼 SVM은 특성 스케일에 민감하므로, 보통 사이킷런의 StandardScaler을 사용하면 결정경계의 명확성을 높일 수 있다.

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris() # 사이킷런 빌트인 iris 예제 데이터 로드
x = iris['data'][:,(2,3)] # 꽃잎의 길이, 너비 변수 사용
y = (iris['target']==2).astype('int') # index=2 : Versinica

# 사이킷런의 파이프라인 라이브러리를 통해서 데이터 스케일과 모델 적합을 한번에 할 수 있음.
svm_clf = Pipeline([
                    ('scaler',StandardScaler()),
                    ('linear_svc',LinearSVC(C=1,loss='hinge'))
])

# 모델 훈련
svm_clf.fit(x,y)

# 꽃잎 길이 5.5cm, 너비 1.7cm의 iris 데이터를 예측한다고 가정
new_iris = [[5.5,1.7]]
prediction = svm_clf.predict(new_iris)[0]
print(prediction) # 1 : Versinica : True(1)
> 1

SVM 분류기는 기존 로지스틱 회귀처럼 클래스에 대한 확률, 즉 predict_proba() 메서드를 제공하지 않지만, SVC모델안에 probability=True 매개변수를 주게되면 predict_proba()메서드 사용 가능
위 방법말고, SVC(kernel='linear',C=1)과 같이 SVC 모델을 사용 가능 (훈련세트가 커지면 속도 느려져 권장 X)
위 방법말고, SGDClassifier(loss='hinge',alpha=1/(m*C)) <m = 샘플수>를 사용 할 수 있다. 이는 LinearSVC만큼 빠르게 수렴하지는 않지만 데이터셋이 아주 커서 메모리에 적재 불가능하거나, 온라인 학습으로 분류 문제를 다룰 때는 유용하다.

- 비선형 SVM 분류

선형 SVM이 많은 경우에서 잘 작동하지만, 데이터셋 자체가 선형으로 잘 분류할 수 없는 경우도 많다.
간단히 이러한 데이터셋에서는 다항 특성(polynomial)인 아래와 같은 특성을 추가하면 된다.

import matplotlib.pyplot as plt
x = np.linspace(-3,3,10)
y = np.linspace(1,1,10)
plt.scatter(x,y)
plt.grid()
plt.show()

b_func = x**2
plt.scatter(x,b_func)
plt.grid()
plt.show()

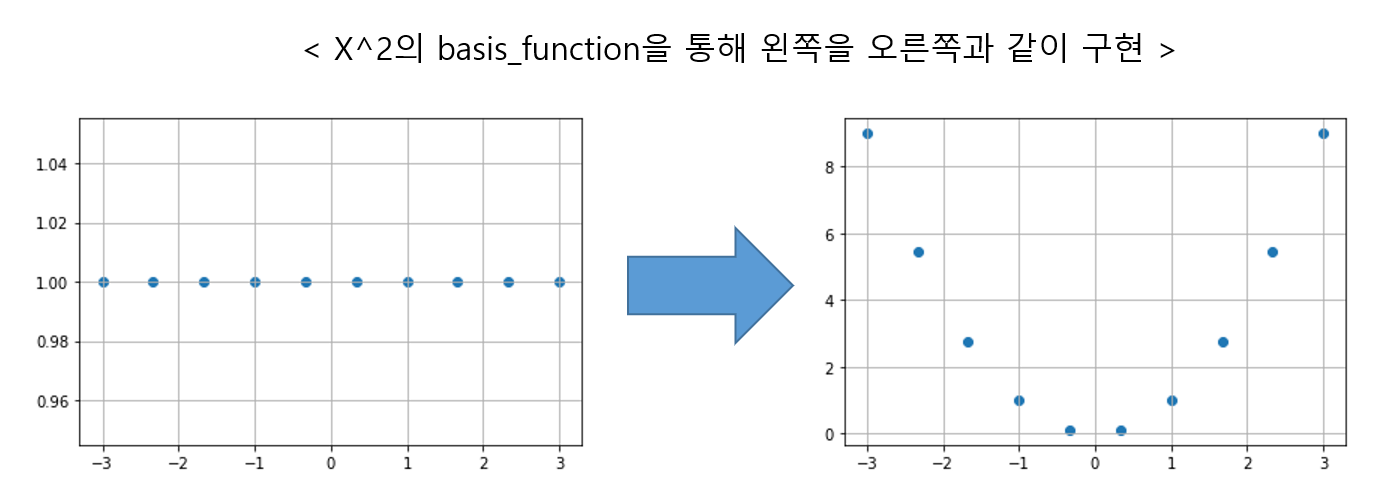
위 과정은 사이킷런의 PolynomialFeature를 사용하면 데이터에 다항특성을 적용할 수 있다.
다음은 실제 비선형적 특성을 가지는 사이킷런의 moons데이터 예제를 통해 비선형 SVM 분류를 해보겠다.

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.svm import LinearSVC

# 샘플 수 1000개, noise값 0.1, random_state=2021
x,y = make_moons(n_samples=1000,noise=0.1,random_state=2021)

# 변수변환 : polynomial 3차 다항식 사용, scaler : StandardScaler 사용, 모델 : LinearSVM(C=10,loss='hinge) 사용 
polynomial_std_svm = Pipeline([
                               ("polynomial",PolynomialFeatures(degree=3)),
                               ("std",StandardScaler()),
                               ("svm",LinearSVC(C=10,loss='hinge'))
])

# 모델 학습
polynomial_std_svm.fit(x,y)

# 첫번째 변수값:2.0, 두번째 변수값:1.0 인 새로운 데이터 예측
new_moon = [[2.0,1.0]]
polynomial_std_svm.predict(new_moon)
> array([1]) # True

hinge loss 부가 내용은 아래와 같다.

- 커널(다항식, 가우시안 RBF)

✔ 다항식 커널

다항식 특성(PolynomialFeatures)을 추가하는 것처럼 간단하고 모든 머신러닝 알고리즘에서 잘 동작한다.
하지만 낮은 차수의 다항식은 복잡한 모델을 표현하기 쉽지 않기 때문에, 굉장히 많은 차수를 사용하여서 모델을 학습해야한다.
그런데 많은 차수를 사용한 모델은 학습속도를 무시무시하게 떨어트리고 심지어 동작 자체를 안하는 경우도 있다.
데이터 변환을 통해 비선형적인 데이터를 분류를 하고 싶고, 모델 학습에도 지장을 주지 않는 효율적인 방법은 없을까라는 고민끝에, SVM을 사용할 땐 kernel trick이라는 수학적 기교를 사용할 수 있다.
실제로 특성을 추가하지 않았음에도, 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있다.
다시 moons 데이터셋을 통해 연습해보겠다.

from sklearn.svm import SVC
# kernel='poly(degree=3)'사용
# 매개변수 coef0는 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조절하는 것
# coef0을 적절한 값으로 지정하면 고차항의 영향을 줄일 수 있다. (coef0의 default=0)
poly_kernel_std_svm = Pipeline([
                            ("std",StandardScaler()),
                            ("poly_kernel_svm",SVC(kernel='poly',degree=3,coef0=1,C=5))
])
poly_kernel_std_svm.fit(x,y)

✔ 가우시안 RBF 커널

다항 특성 방식과 마찬가지로 유사도 특성 방식을 모델에 적용할 수 있다.
다항식 커널에서 말한 것과 같이 추가 특성을 계산하려면 엄청난 시간과 비용이 발생한다. (특히 훈련 세트가 클 경우 심해짐)
하지만 마찬가지로 커널 트릭 방식을 사용하면, 실제 특성을 추가하지 않고 유사도 특성을 많이 추가한 것과 같은 효과를 얻을 수 있다.

# 하이퍼파라미터 r는 규제 역할을 한다.
# (모델이 과적합일 경우=> r 감소시키고, 모델 과소적합일 경우=> r 증가시켜야함)
# 하이퍼파라미터 C도 r(gamma)와 비슷한 성격을 띈다.
# 그래서 모델 복잡도를 조절하기 위해서 gamma와 C를 함께 조절해야 한다.
# Tip (하이퍼파라미터 조절) : 그리드 탐색법 사용(그리드 큰 폭 => 그리드 작은 폭) : 줄여가면서 탐색
rbf_kernel_std_svm = Pipeline([
                               ('std',StandardScaler()),
                               ('rbf_kernel_svm',SVC(kernel='rbf',gamma=3,C=0.001))
])
rbf_kernel_std_svm.fit(x,y)

이전 장에서 배운 regression과 오늘 배운 classification 이론 및 모형들 통해서 전반적인 supervised learning의 이해 및 인지적 구조가 형성되었을 것이다. 앞으로 배울 decision tree, ensemble의 내용도 이러한 인지적 구조속에서 크게 벗어나지 않고, 방법적인 측면에서 새로운 인사이트를 제공할 뿐이니 함께 재밌게 앞으로 나아가 봅시다!