[프로그래머스] Lv1 소수 찾기

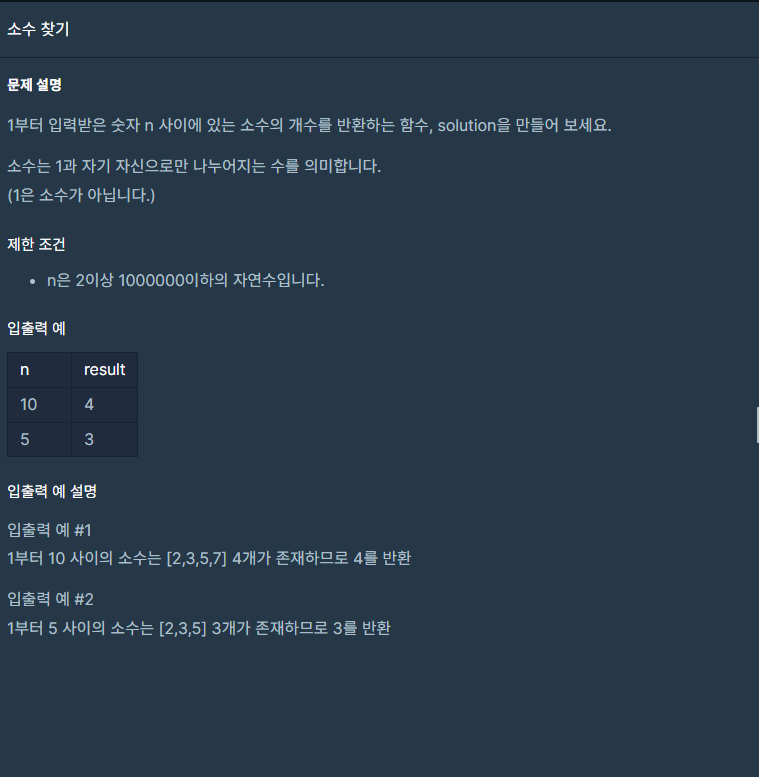
문제설명

해결방안

(1) n까지의 숫자중 소수를 찾자

코드

class Solution {
    public int solution(int n) {
         int answer = 0;
        
        for(int i= 2; i<=n ;i++) {
        	int cnt = 0;
        	for(int j = 1 ; j<=Math.sqrt(i) ; j++) {
        		if( i  % j == 0) {
        			cnt++;
        		}
        		if(cnt >1 ) {
        			break;
        		}
        	}
        	if(cnt == 1) {
        		answer++;
        	}
        }
        return answer;
    }
}

내 코드 설명

(1) 2 ~ i의 제곱근까지의 숫자중 1을 제외한 다른 약수를 가질 경우 노카운트
(2) 1만을 약수로 가질 경우만 카운트 하였다.

다른 사람 풀이

	public String[] solution(String[] strings, int n) {
	            int answer = 0;
        int [] arr = new int [n+1];
        for( int i = 2 ; i<= n ; i++) {
            arr[i] = i ;
        }

        for(int i = 2; i<= n  ; i++) {
            if(arr[i]== 0 ) {
                continue;
            }
            for(int j = i* 2 ; j<=n ; j+=i) {
                arr[j] = 0 ;
            }
        }

        for(int i = 2 ; i<=n ;i++) {
            if( arr[i] != 0 ) {
                answer++;
            }
        }
        return answer;
	}

다른 사람 코드 설명

(1) 느낀점에서 설명..

느낀점

시간복잡도 문제가 가장 어려운 것 같다..
에라토스테레스의 체 라는 방법이 있다는 것을 아예 몰랐다. 에라토스테레스의 체란 2~ n까지의 정수를 나열하여 그중 가장 작은 수의 배수들을 삭제시키고 남은 수들중 다시 가장 작은 수의 배수들을 삭제 시키는 방법이다. 이렇게 하면 시간복잡도의 문제를 줄일 수 있는 가장 좋은 방법인 것 같다.
에라토스테레스의 체 알고리즘 기억하자!