[프로그래머스] Lv1 소수 만들기

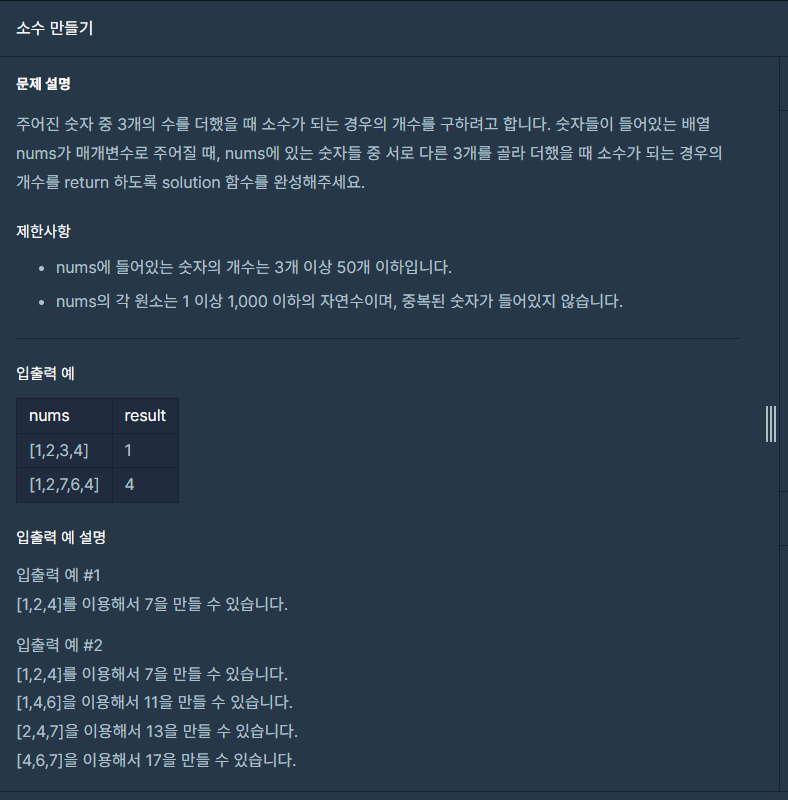
문제설명

해결방안

(1) 조합만 다르다면 합이 같아도 카운트 되므로 반복문을 돌려서 나오는 경우의 수 리스트에 넣고 소수 판별하자

코드

import java.util.*;
class Solution {
    public int solution(int[] nums) {
     int answer = 0;
        
        List list = new ArrayList();
        
        for(int i= 0;  i< nums.length;i++) {
        	
        	for(int j = i+1; j < nums.length;j++) {
        		
        		for(int k = j+1 ; k<nums.length ; k++) {
        			int sum = 0 ; 
        			sum = nums[i] + nums[j] + nums[k];	
        			list.add(sum);
        		}
        	}
        }
        
        for(int i =0; i <list.size();i++) {
        	int cnt = 0 ;
        	for(int j = 1 ; j<=(int) list.get(i) ; j++) {
        		if( (int) list.get(i) % j ==0 ) {
        			cnt++;
        		}
        	}
        	if(cnt == 2 ) {
        		answer ++;
        	}
        }
        
        return answer;
    }
}

내 코드 설명

(1) 3중 for문을 통해 각 자리에 해당하는 세 가지 조합을 모두 리스트에 추가
(2) 추가한 리스트에서 소수 판별하여 1과 자기자신만을 약수로 가질 경우 cnt 카운트 하여 2개일 때 answer값 증가

다른 사람 풀이

	import java.util.Arrays;

class Solution {



    public int solution(int[] nums) {
        int ans = 0;

        for(int i = 0; i < nums.length - 2; i ++){
            for(int j = i + 1; j < nums.length - 1; j ++){
                for(int k = j + 1; k < nums.length; k ++ ){
                    if(isPrime(nums[i] + nums[j] + nums[k])){
                        ans += 1;  
                    } 
                }
            }
        }
        return ans;
    }
    public Boolean isPrime(int num){
        int cnt = 0;
        for(int i = 1; i <= (int)Math.sqrt(num); i ++){
            if(num % i == 0) cnt += 1; 
        }
        return cnt == 1;
    }
}

다른 사람 코드 설명

(1) 나와 다르게 리스트 선언 없이 소수 판별하는 함수만 만들어 바로 마지막 for문에서 함수 호출하여 소수 판별 후 결과값 증가시켰다.

느낀점

함수를 만들어 호출하는 습관을 들여야겠다. 코드가 길어졌을 때 확실히 가독성이 좋고 유지보수가 좋을 것 같다는 생각이 들었다.