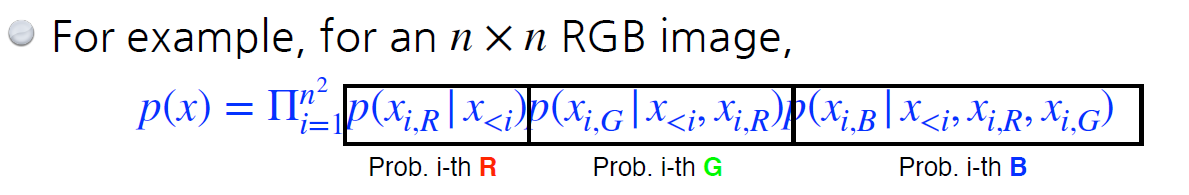[BoostCamp AI Tech / Day 10, DL basic] Sequential Models -Generative Models (1/2)
[boostcampAI U stage] week2
Generative model
- what does it mean to learn a generative model(생성 모델)?
- Suppose we ard given images of dogs.
- We want to learn a probability distribution such that
- generation: If we sample show look like a dog(sampling)
- Density estimation: should be high if x looks like a dog, and low other wise(anomaly detection, 이상치 탐지)
- Also known as, explicit models
- Unsupervised representation learning: We should be able to learn what these images hahve in common, e.g., ears, tail, etc(feature learning)
- Then, how can we represent ?
image들이 주어졌을 때 어떠한 task를 할 수 있을까?
예를 들어, GAN처럼 강아지 이미지를 sampling한 다음 서로 다른 강아지의 이미지를 생성해내는 것 뿐만 아니라 입력에 확률 값 를 기반으로 이상행동탐지과 같은 기능도 수행할 수 있다.
이처럼, Generative Model은 입력이 주어졌을 때 입력에 대한 확률값을 얻어낼 수 있는 model을 explicit models이라 하고, GAN이나 VAE처럼 generation만 할 수 있는 모델을 implicit models 이라 한다.
또한 강아지의 귀가 2개, 코 1개, 꼬리가 있는 등과 같이 이미지가 주어졌을 때 특징을 학습하는 자기지도학습도 수행할 수 있다고 한다.(by 스탠포드 강의...)
그렇다면, 는 어떻게 만들까?
Basic Discrete Distribution
-
Bernoulli distribution: (biased) coin flip
- D = {heads, Tails}
- Specify P(X = Heads) = p. Then P(X=Tails) = 1-p
- Write X ~ Ber(P)
- 확률값을 표현하는 파라미터는 1개만 있으면 됨
-
Categorical distribution: (biased) m-sided dice.
- D = {1,2,...,m}
- Specify P(Y=i) = , such that
- Write: Y~Cat
- 확률값을 표현하는 파라미터는 m-1개만 있으면 됨
- m-1개가 정해지면 자동적으로 나머지 1개는 정해지기 때문
-
주어진 학습 데이터의 확률 분포를 찾아내기 위해 몇 개의 파라미터가 필요한지 먼저 찾아야 한다.
E.G-1
예를 들어, RGB의 결합분포를 보면
R,G,B는 각각 0~255 gray scale 값을 가질 수 있다.
따라서 각각 256개로 표현이 가능하므로, 모든 경우의 수는 256x256x256이다.
그렇다면, RGB를 모두 표현하는 파라미터는 몇개일까?
바로 (256x256x256 - 1 )개이다
여기서 말하고자 하는 것은, 한 pixel을 표현하는데 매우 많은 파라미터가 필요하며, 이미지가, 수천 수만장이면 그 개수만큼 파라미터가 더 필요하게 된다.

E.G-2
더 쉽게, 흑백의 이미지가 있으면, 각 pixel은 1과 0으로 표현이 가능한데, 이미지가 28 x 28일 경우 총 784개의 pixel로 경우의 수는 이다.
따라서 한 이미지를 표현하기 위해 필요한 파라미터 개수는 총 이다.
여기서, 우리가 알고 있단 사실은, 기계학습에서 파라미터의 개수가 증가할수록 학습이 어려우며, normalization performance가 저하된다.
그렇다면 파라미터의 개수를 줄일 수 있는 방법은 무엇이 있을까?
단, GPT, hyper clova같은 거대 AI 모델이 나오고, 그것과 관련된 논문들(Scaling Laws for Meural Language Models)이 나오며 트렌드가 바뀌긴 했다. 하지만 현재 강의는 그 전에 만들어진 것이므로 어느 정도 가만하고 들으려고 한다.

parameter reduction
우선, 이미지에 있는의 n개 pixel들이 모두 independent하다고 가정을 하면
이 이미지를 표현할 수 있는 경우의 수는 기존과 같이 개 지만,
parameter의 개수는 개가 된다
- 각 pixel이 독립이라 각 픽셀을 표현하는데 2개의 파라미터가 있지만, 하나가 정해지면 다른 하나는 자동적으로 지정되기 때문이다.

하지만, fully dependent는 너무 파라미터 개수가 많고, fully independent는 너무 파라미터 개수가 줄이드니 그 중간 지점을 잘 고려해보고자 한다.
아래 주어진 Chain rule, Bayes' rule은 주어진 x가 끼리 의존인지 독립인지 상관이 없지만, conditional indepenence는 x,y가 독립일 때만 성립한다. 이 방법들을 통해 파라미터 개수를 줄여보고자 한다.

우선 chain rule을 보면, 결국 n개가 주어졌을 떄의 parameter 개수는 로 기존과 똑같다.

그렇다면, 여기서 Markov Assumption(현재 상태는 이전 상태에 대해서만 영향을 받는다) + 현재 상태는 이전 상태에만 독립적인 조건을 추가한 경우, 개의 파라미터만 남게 된다.
이처럼 conditional indepent assumption을 어떻게 정할지에 따라 파라미터의 개수가 달라지며, Auto-regressive model(AR)은 conditional indepency를 활용한다.

Auto-regressive Model
- 즉, 조건부 도긻을 이용해 파라미터 개수를 줄인 모델로,
- 특정 시점의 이전 값들에 대한 선형 조합을 이용하여 관심 대상을 예측하는 모델이다.
- 마르코프 가정에 의해 t번째 값이 t-1번째에만 종속하는 것 뿐만 아니라, t-1 : 1까지 종속하는 것도 AR model이다.
- 이전 n개를 고려: AR-n model
- 단, 조건부 독립 조건에 따라 전체 모델의 구조가 달라진다.
- 단, 여기서 중요한 건 ordering이다.
- 28x28 image의 pixel을 예로 들면, 어떤 방향으로 순서를 매기는지에 따라 결과가 다 다르다.
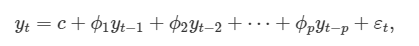
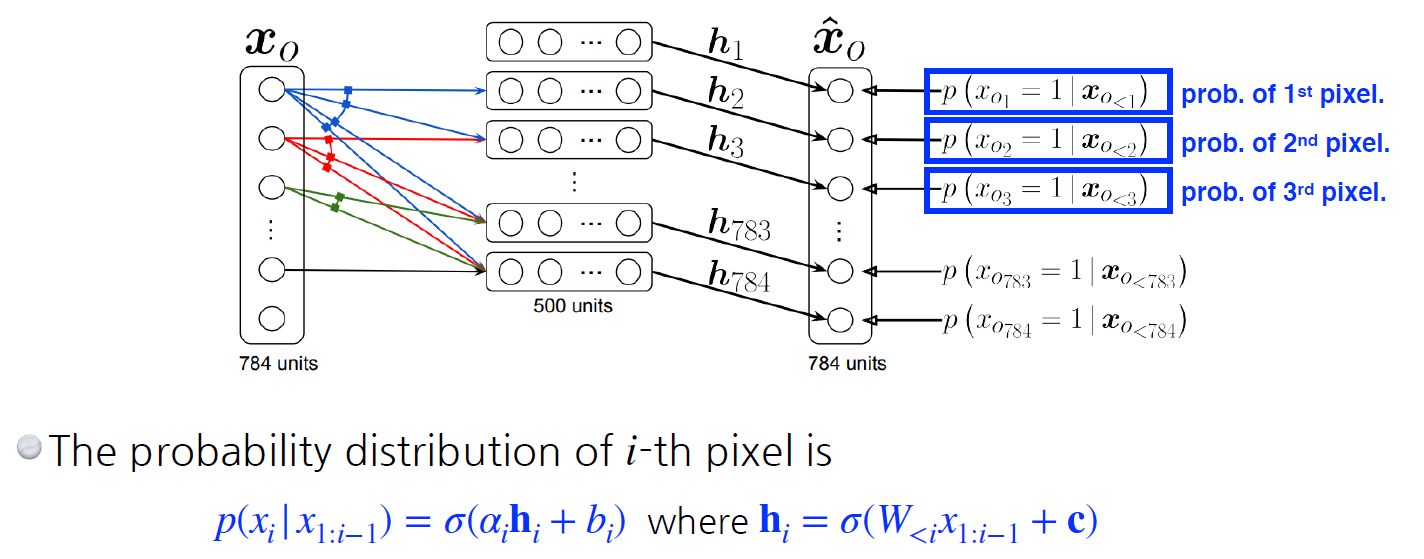
NADE: Neural Autoregressive Density Estimator
- NADE의 조건부 독립 조건은 i 번째는 1:i-1번째에 의존적
- explicit model로 확률을 계산할 수 있음
- continuous random variable이라면, 마지막 layer에 Gaussian mixture 모델을 활용하여 continuous distribution
Pixel RNN
- Pixel을 만들기 위한 AR 모델
- RNN을 통해 pixel을 generation(NADE는 Dense layer를 사용)
- i 번째 pixel에 R을 먼저 만들고 G,B만듬
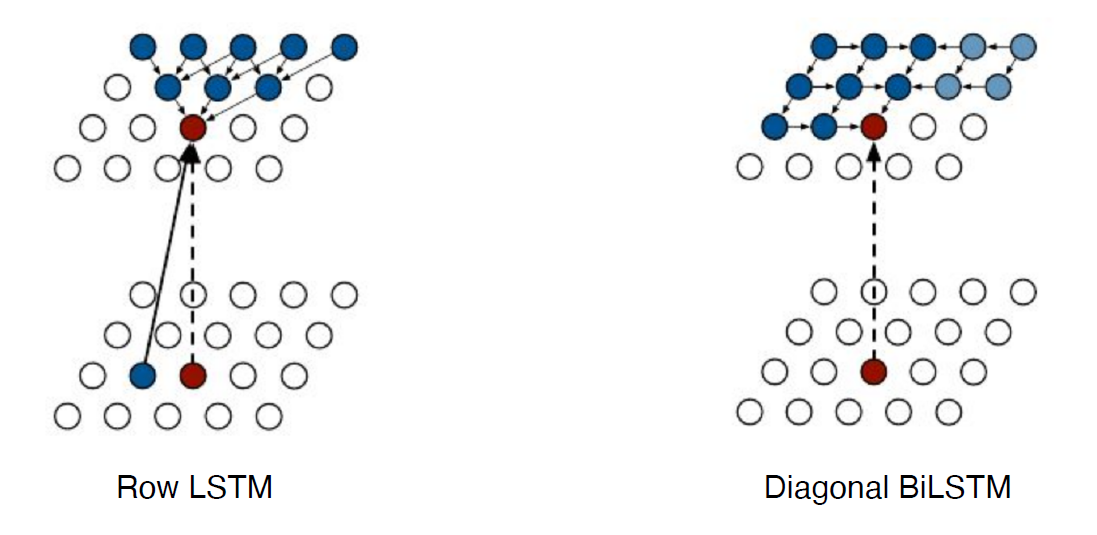
- Row LSTM, Diagonal BiLSTM 모델들이 있음
- Row LSTM: i번째 pixel을 생성 시 윗쪽 입력을 사용
- Diagonal BiLSTM: i번째 pixel 생성 시 이전 입력을 모두 사용