벡터

• 벡터란?

  • 공간에서의 한 점으로 나타내며
  • 원점으로부터 상대적 위치를 표현
  • 벡터에 숫자(스칼라)를 곱해주면 벡터의 길이가 변함
  • 벡터에 곱해주는 스칼라값이 0보다 작으면 벡터 방향이 바뀜

• 숫자를 원소로 가지는 리스트(list) 또는 배열(array)

• x = $\begin{bmatrix} 1 & 7 & 2\end{bmatrix}$ 열벡터

• x = $\begin{bmatrix} 1 \\ 7 \\ 2\end{bmatrix}$ 행벡터

• 파이썬 코드

  x = [1,7,2] or x= np.array([1,7,2)

• 벡터의 차원 : 벡터의 원소 개수

벡터의 연산

• 벡터 끼리의 덧셈과 뺼셈 : 같은 위치의 원소끼리의 연산
  • 단 동일 차원의 벡터끼리만 연산이 가능
• 벡터의 성분곱(element-wise) : 같은 위치의 원소끼리 곱셈
• x = $\begin{bmatrix} 1 & 7 & 2\end{bmatrix}$
  y = $\begin{bmatrix} 5 & 2 & 1\end{bmatrix}$
  x + y = $\begin{bmatrix} 6 & 9 & 3 \end{bmatrix}$
  x - y = $\begin{bmatrix} -4 & 5 & 1 \end{bmatrix}$
  x * y = $\begin{bmatrix} 5 & 14 & 2 \end{bmatrix}$ 성분곱
• 두 벡터의 덧셈 혹은 뺄셈은 다른 벡터로부터 상대적 위치 이동을 표현

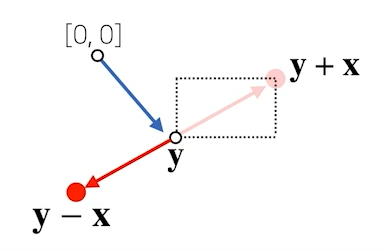
벡터의 노름

• 벡터의 노름 : 원점으로부터의 거리, $||x||$ 기호는 노름(norm)이라 부름

  • L1 norm : $||x||_1 = {\sum_{i=1}^{d} |x_i|}$

    • $L_1$-노름은 각 성분의 변화량의 절대값

  • L2 norm : $||x||_2 = {\sqrt{\sum_{i=1}^{d} |x_i|^2} }$

    • $L_2$-노름은 유클리드 거리
    • norm은 임의의 차원 d에 대해서 성립하는 것을 명심

        #L1-노름
        def l1_norm(x):
            x_norm = np.abs(x)
            x_norm = np.sum(x_norm)
            return x_norm
    
        #L2-노름
        ##L2-노름은 np.linalg.norm을 이용해도 구현 가능
        def l2_norm(x):
            x_norm = x*x
            x_norm = np.sum(x_norm)
            x_norm = np.sqrt(x_norm)
            return x_norm
        ```

• 노름별 기하학적 성질
  

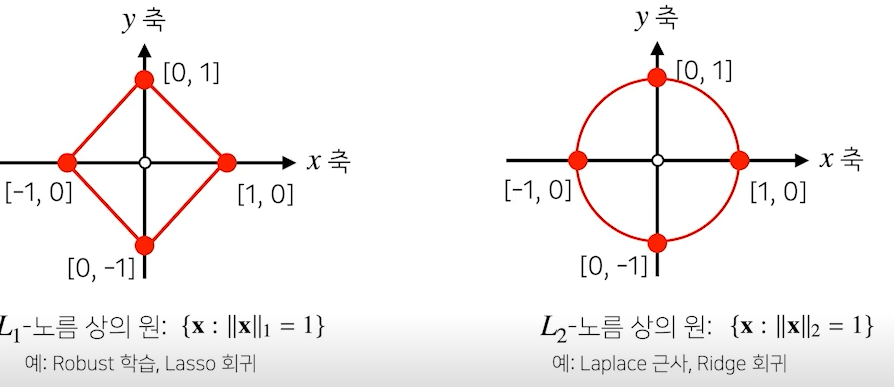
  • 노름별 거리를 정의하는 방식이 다르기 때문에 다른 기하학적 성질을 지님
  • 이러한 다른 성질을 바탕으로 기계학습에서 학습이나 정규화를 진행

• 두 벡터 사이의 거리(뺄셈)

  • 성분별로 뺄셈을 하므로 교환법칙 성립
    • $||x-y|| = ||y-x||$

• 두 벡터 사이의 각도($L_2||$-노름만 가능)
  

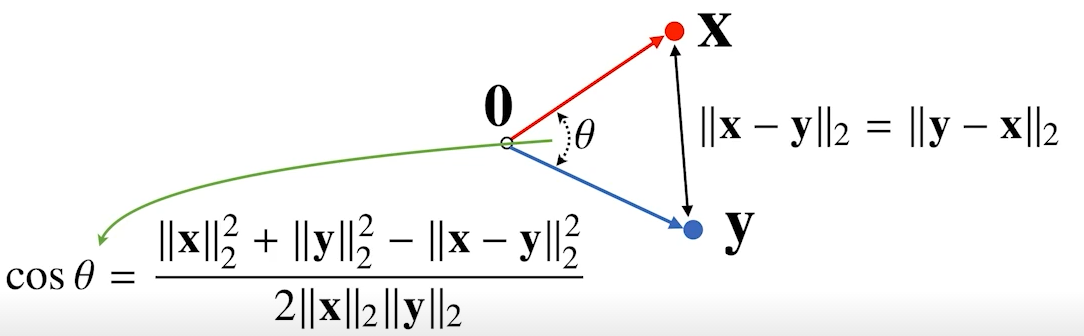
  • 유클리드 거리를 이용하여 두 점사이의 거리를 구할 수 있으면,
  • 제2 코사인 법칙을 이용해서 각도 계산 가능
  • 내적을 통해서도 쉽게 계산이 가능
    • 내적 : 적을 쌓는다는 뜻으로, 여기서는 곱하다의 뜻
      • 즉, 내적은 벡터를 마치 수처럼 곱하는 개념
      • 내적의 기호는 $(\cdot)$이고, 벡터의 크기를 절대값으로 표시(스칼라)
        • 내적 공식 : $\vec{a} \cdot \vec{b} = {|\vec{a}||\vec{b}|cos\theta}$
        • 여기서 $\vec{a} \cdot \vec{b}$ 는 성분곱의 합 => $<x,y> = {\sum_{i_1}^{d}x_iy_i}$
      • 내적 해석

        • 벡터 b에 정사영(orthogonal Projection)된 벡터의 길이 $|a|cos\theta$ 만큼 벡터 b의 길이를 조정한 것

          

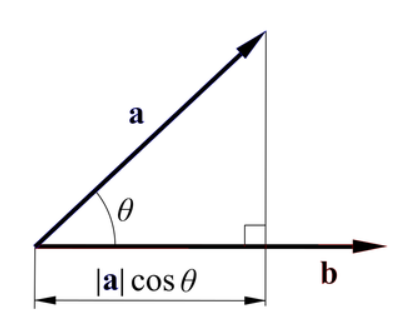
        사진 출처 : https://wikidocs.net/22384

  • 따라 내적 공식을 변환하여 우변을 $cos\theta$만 남기면 $L_2$-노름의 수식과 분자만 다르며, 쉽게 사잇각을 구할 수 있음
  • 내적은 numpy의 np.inner()를 이용하여 계산

  def angle(x,y):
      v = np.inner(x,y) / (l2_norm(x) * l2_norm(y))
      theta = np.arccos(v)
      return theta