행렬(matrix)

• 행렬은 벡터를 원소로 가지는 2차원 배열( n x m 행렬)

• 행렬은 행(row)과 열(column)이라는 인덱스(index)를 가짐

• 열 벡터 : $x_{11}$~$x_{n1}$ 로이 루어진 벡터

• 행 벡터 : $x_{11}$~$x_{1m}$ 로이 루어진 벡터

• $X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}$

  # numpy array
  X = np.array([[1,-,2,3],[7,5,0],[-2,-1,2]])
  # 3x3 matrix
  

전치행렬

• 행과 열의 인덱스가 바뀐 행렬
• $X^{T}$ => $X_{ij}$ 의 원소가 $X_{ji}$로 이동
• 대각성분은 변하지 않고 나머지 원소들이 바뀜
• 벡터에 적용할 경우, 열벡터 => 행벡터, 행벡터 => 열벡터

행렬 이해(1)

• 벡터를 공간에서의 한 점을 의미한다면 행렬은 여러 점들의 집함
• 여기서 벡터를 각각의 데이터로 본다면 행렬은 데이터를 모아놓은 집합체
  - 행렬 $X$에서 $X_i$는 i번쨰 데이터, $X_{ij}$는 i번째 데이터의 j번째 변수 값
  

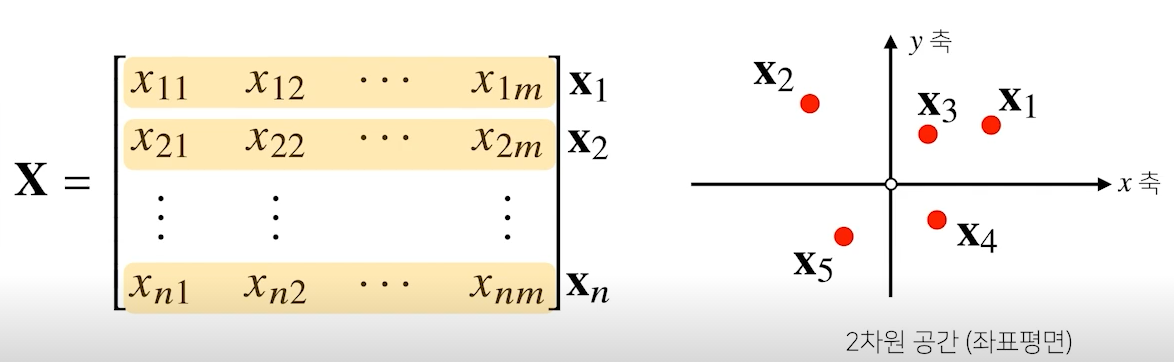
행렬의 연산

• 같은 모양을 가지면 덧셈, 뺄셈 연산, 성분곱(element-wise) 가능

• 성분곱 표시 : $X \bigodot Y = {(x_{ij}y_{ij})}$

• 스칼라곱은 행렬의 각 원소에 스칼라값을 곱함

• 행렬 곱셈(matrix multiplication) : i번째 행 벡터와 j번째 열벡터 사이의 내적 : $XY = {(\sum_k x_{ik}y_{kj})}$
  $X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ x_{21} & x_{22} & \cdots & x_{2m} \\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nm} \end{bmatrix}$ $Y = \begin{bmatrix} y_{11} & y_{12} & \cdots & y_{1l} \\ y_{21} & y_{22} & \cdots & y_{2l} \\ \vdots & \vdots & & \vdots \\ y_{m1} & y_{m2} & \cdots & y_{ml} \end{bmatrix}$

  • XY : $X(n,m)Y(m,l) = n \times l$ 크기의 행렬

  X = np.array([[1,2,3],[7,5,0]])
  Y = np.array([[0,1],[1,-1],[-2,1]])
  
  # numpy 행렬곱셈 : @ 연산 사용
  X @ Y
  >> array([[-8, 6],[5,2]])

• 주의

  • 행렬 곱셈은 행벡터와 열 벡터 사이의 연산
  • numpy에서 @ 연산 : 행렬 연산(행벡터 X 열벡터) != np.inner 내적(행벡터 X 행벡터)
    • np.inner로 행렬곱셈을 수행하고자 할 경우, 두 행렬 중 하나를 전치행렬로 변환 후 연산을 수행할 것
    • 즉, numpy의 내적 inner와 수학의 내적은 다르므로 주의
    • 수학의 내적 : $XY = {(\sum_k x_{ik}y_{kj})}$ = $np.inner(XY^T)$
    • numpy의 내적 : $XY = {(\sum_k x_{ik}y_{jk})}$ = $np.inner(XY)$

행렬 이해(2)

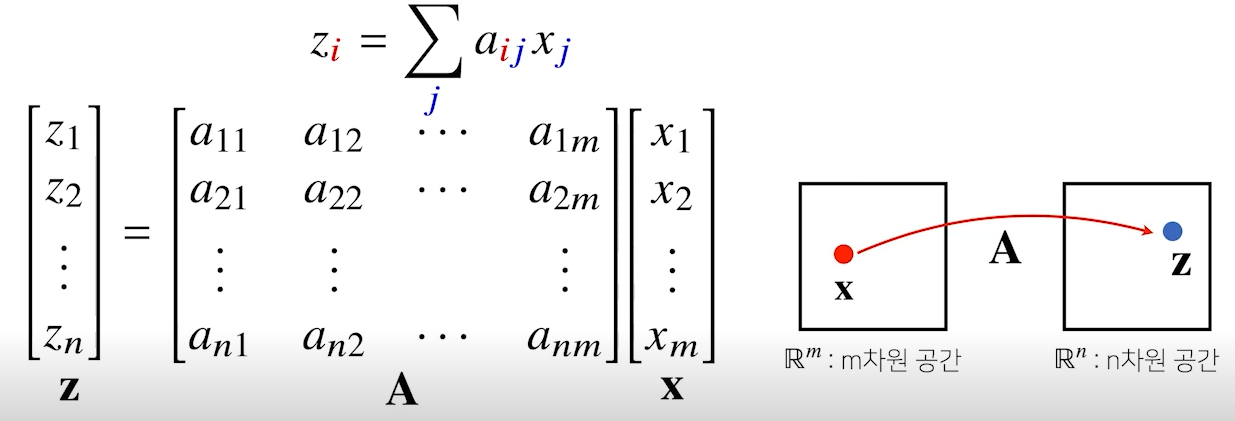
• 행렬은 벡터 공간에서 사용되는 연산자(operator)
• 행렬곱을 통해 벡터를 다른 차원으로 이동
• 행렬곱을 통해 패턴을 추출할 수 있고, 데이터 압축도 가능
• 모든 선형변환(linear transform)은 행렬곱으로 계산 가능
  

역행렬 이해하기

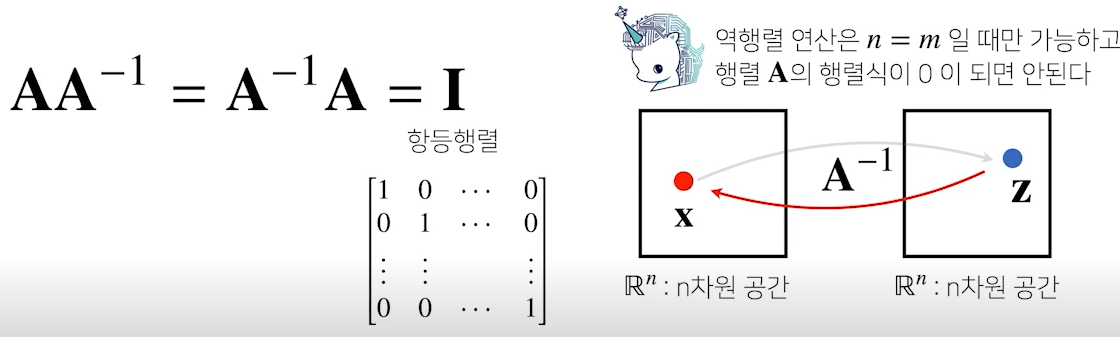
• 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)라고 부르고 $A^{-1}$라 표기

• 역행렬은 행과 열의 개수가 같고, 행렬식(determinant)이 0이 아닌 경우에만 계산 가능

  • 행렬식 계산 방법 : https://engineershelp.tistory.com/297

• 행렬 A와 A의 역행렬의 연산 결과는 I라는 항등행렬(identity matrix, 대각성분은 1 나머지는 0)이 출력됨
  

• numpy에서 행렬식 구하는 방법 : np.linalg.inv()

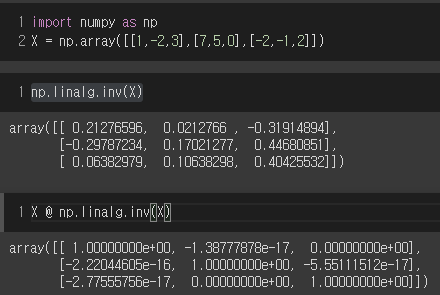
  • 컴퓨터로 수행하는 연산이기에 대각성분을 제외한 나머지가 거의 0에 가까운 값으로 출력됨

    

• 만약, 행과 열이 다르게 되면 역행렬을 구할 방법은 없는지?

  • 연산을 되돌린다는 개념으로 접근하게 되면, 유사 역행렬(pseudo-inverse) 또는 무어 펜로즈(Moore-Penrose) 역행렬 $A^+$를 이용
  • 행과 열의 개수가 달라도 역행렬과 완전히 같지 않지만, 유사한 기능을 하는 유사 역행렬을 구할 수 있음
  • 단 행과 열의 개수에 따라 계산 방식이 달라짐
    1) $n >= m$ 인 경우 $A^+={(A^TA)^-1A^T}$, $A^+A = I$만 성립
    2) $n <= m$ 인 경우 $A^+={A^T(A^TA)^-1}$, $AA^+ = I$만 성립

    

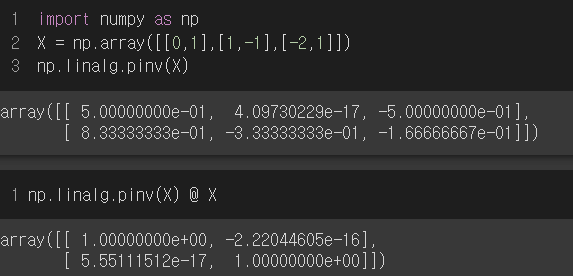
유사 역행렬 응용

• 응용 1) 변수의 개수가 식의 개수보다 많은 연립방정식
  • n <= m(해)인 경우이므로 유사역행렬 2) 방식으로 풀기
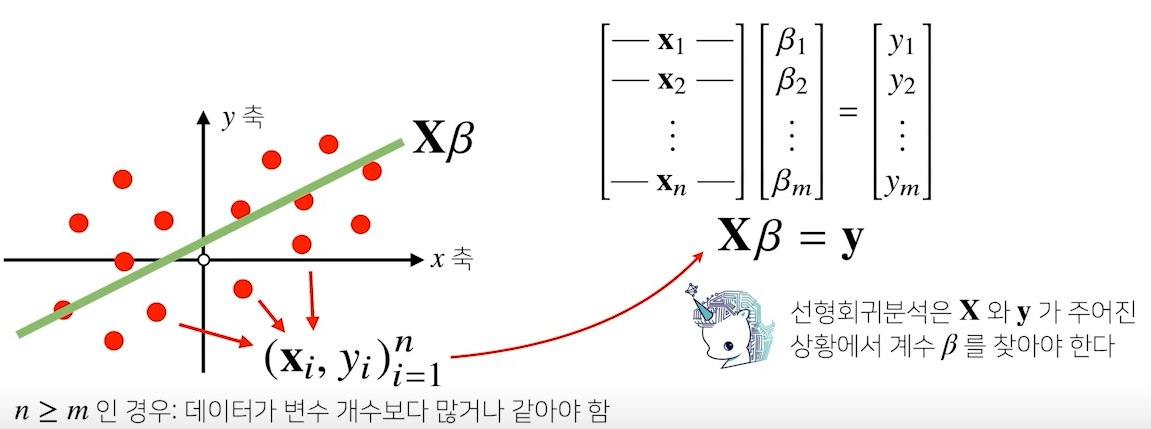
• 응용 2) 선형회귀분석
  • np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있음
  • 단, 행의 개수가 열의 개수보다 X -> Y를 만족하는 $\beta$를 찾는 것은 불가능하고, 최대한 X 계수를 잘 설명해줄 수 있는 선형회귀식을 찾는 것이 최선
  • $X\beta=\hat{y}\approx y$, $\underset{\beta}{min}||y-\hat{y}||_2$
  • 예측한 $\hat{y}$값과 실제 $y$값의 차이($L_2$-노름)가 최소화가 되는 $\beta$를 찾는 것이 잘 예측했다고 표현할 수 있음
    
  • sklearn의 LinearRegression과 같은 결과
    • 단 결과가 다르게 나올 수도 있는데, sklearn의 선형회귀는 y절편(bias)도 포함하고 있음
    • 유사역행렬로 구한 선형회귀식에 y절편을 포함 시 동일한 결과가 출력됨