• 신경망 모델
  • 기본적으로 비선형 모델인데
  • 실제로는 신경망 모델을 수식적으로 파해쳐보면 선형 모델과 비선형 함수로 이루어진 모델
  • 실제 모델의 동작 방식과 비선형 학습 패턴에 대한 이해가 필요

    

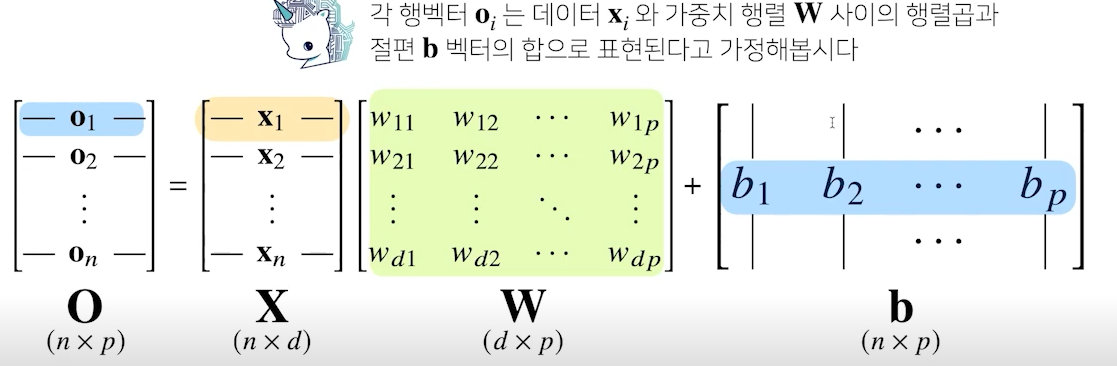
  • X : 전체 데이터가 모여있는 행렬, 각 행데이터는 각 데이터 포인트
  • W : 가중치 행렬 W, 다른 데이터 공간으로 변환해주는 역할
  • b : y절편 벡터들의 행렬, $b_1~b_p$까지 모든 행에 대해서 동일한 값 적용
  • O : 출력 데이터 행렬, 입력 데이터의 입력 데이터 형태와 가중치 데이터 형태에 따라 출력 데이터의 형태가 달라짐
    • d개의 입력 변수를 p개의 선형 모델을 만들어서 p개의 잠재 변수 생성

---

신경망 이해

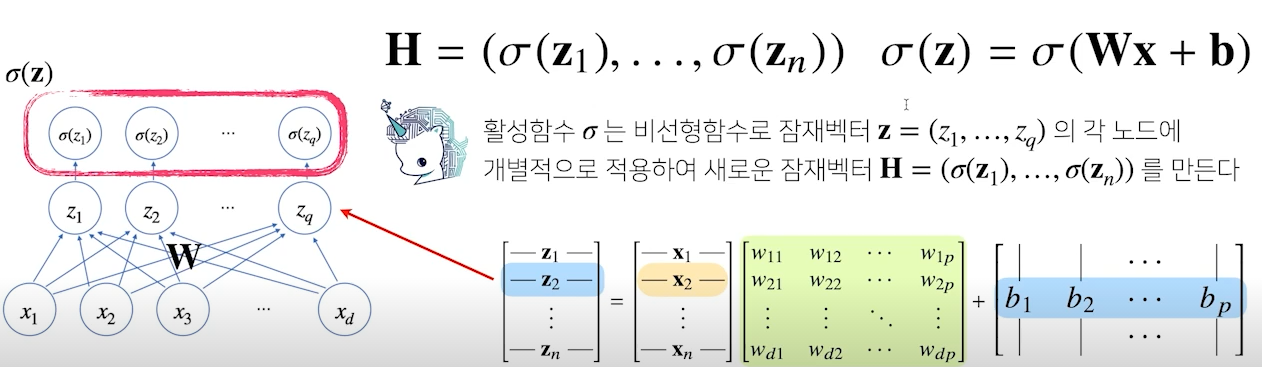
• 신경망은 선형 모델과 활성함수(activation function)를 합성한 함수
• regression 문제가 아닌 Classification 문제에선 이진 분류 시, sigmoid, 다중클래스 시 softmax actvation 함수를 활용
• activation 함수는 선형의 출력을 비선형 모델에 맞는 값(분류 클래스별 확률값)으로 변환
• activation 함수를 통해 Dense layer의 각 노드가 확률값을 갖게 되며, 그 값들을 모아놓은 벡터를 잠재벡터 $H = ({\sigma(z_1),\cdots,\sigma(z_n)})$라고 한다.
  (이부분은 조금 확인이 필요할 것으로 보임, 강의 내에서 activation function과 softmax 함수도 개별적인 존재로 다뤘는데, 왜 그런지도 확인이 필요할 것으로 보임
  ※ 해당 내용을 정리한 강의 내에는 $\sigma$를 activation 함수의 기호로 사용했으니 이 점을 참고)
  • 일반적으로 $\sigma$는 활성화 함수 중 sigmoid를 뜻하는 것으로 알고 있음.. 잘못되었으면 코멘트 부탁드립니다.

    

활성 함수

• activation function(활성함수)은 R 위에 정의된 비선형(nonlinear) 함수로서 딥러닝에서 매우 중요한 개념
• 활성화 함수를 쓰지 않으면, 딥러닝은 선형 모델과 차이가 없음
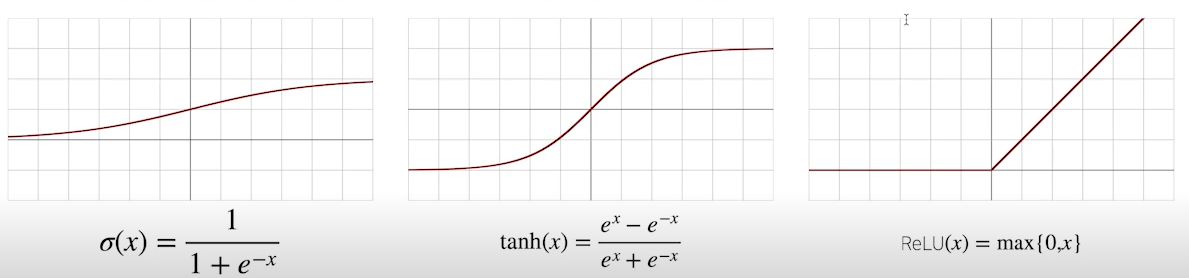
• 시그모이드(sigmoid) 함수나 tanh 함수는 전통적으로 많이 쓰이던 활성화 함수지만 딥러닝에선 ReLU 함수를 많이 쓰고 있음
• sigmoid는 어려번 사용하게 될수록 결국 값이 0으로 수렴하게 되는 문제가 있음, 따라서 이진 분류 문제에서 최종 확률값을 출력해주는 방식으로만 쓰임
• tanh는 RNN model에서 쓰임(LSTM, GRU)

  

softmax

• 소트프맥스(softmax)함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
• 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측
• activation function 중 하나로, 이진분류 이상의 결과를 해석할 떄 사용

• 선형 모델의 결과인 O를 입력으로 받아서, 각 O에 대한 지수함수 값을 분자로하고, 그 지수함수들의 합을 분모로 하여, 각 class별 확률을 반환

• 단, 추론을 할 때는 원-핫(one-hot) 벡터로 최대값을 가진 주소만 1로 출력하는 연산을 하여 softmax로 출력

신경망

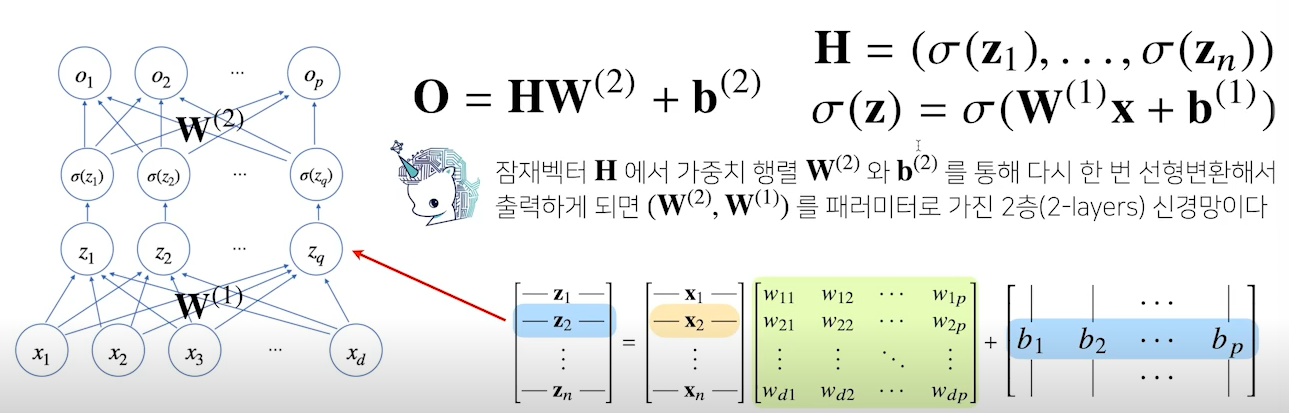
• 신경망은 선형 모델과 activation 함수를 합성한 함수
• 선형 모델과 acivation 함수가 반복적으로 사용되는 모델이 딥러닝의 가장 기본적인 모형

Multi-layer perceptron

다층(Multi-layer)퍼셉트론(perceptron), 줄여서 MLP는 신경망이 어려 층으로 합성된 함수

• H는 Z에 활성화 함수를 적용한 값
• 이 층을 여러 개 쌓은 형태(MLP)
• Z를 출력하는 선형회귀식에서 weight와 bias는 층 개수만큼 행렬의 형태로 생성됨
• 입력부터 출력까지 순차적으로 신경망을 계산하는 것을 순전파(forward propagration)이라 한다

  

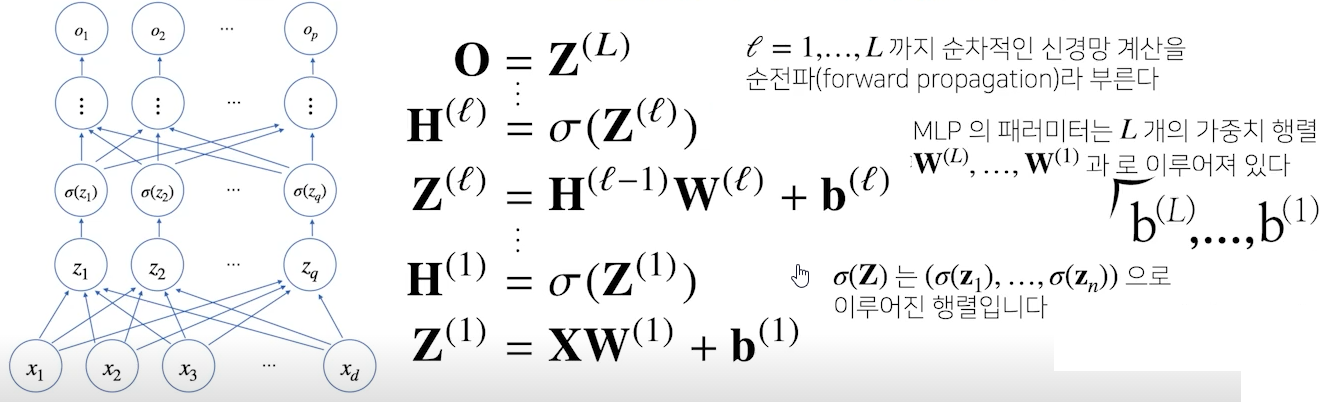
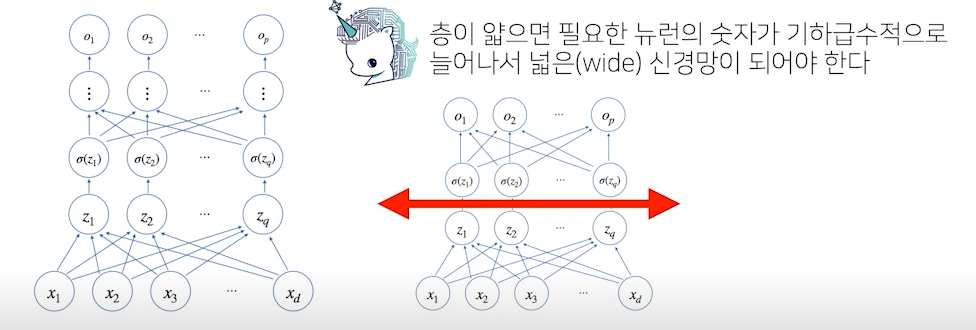
층을 여러개 쌓는 이유

• 이론적으론 2층 신경망으로도 임의의 연속함수를 근사 가능
• 단 층이 깊을 수록 목적 함수를 근사하는데 필요한 뉴런(노드)의 개수가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
  • 적은 뉴런의 개수로 조금 더 빠르게 목적함수로 근사 가능
  • 층이 깊어질수록 적은 파라미터로도 복잡한 함수를 표현 가능
• 복잡한 패턴의 데이터일 경우 조금 더 깊은 신경망을 통해 목적 함수로 근사 가능
• 단, 층이 깊다고 복잡한 함수로 근사를 할 수 있지만, 최적화가 어려워질 수 있음(학습)

  

딥러닝 학습 원리

• 딥러닝은 역전파(backpropagation) 알고리즘을 이용하여 각 층에 사용된 파라미터${W^l, b^l}_{l=1}^L$ 학습
• 학습은 경사하강법을 적용하는데, 각 가중치 행렬을 학습시킬 gradient vector를 계산해야 경사하강법 적용 가능

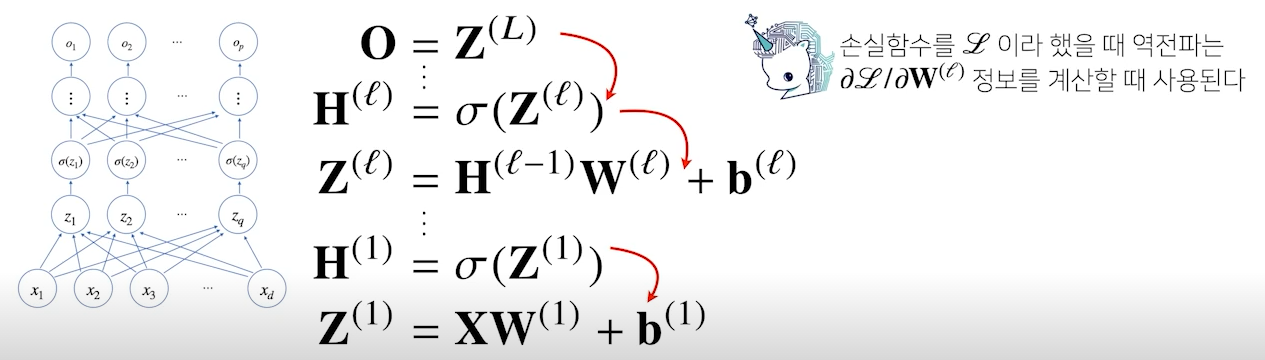
• gradient를 계산할 때는 고층에서 저층(출력층 방향 => 입력층 방향)으로 학습이 진행
• 즉, 각 층 파라미터의 gradient 벡터는 윗층으로부터 역순으로 계산

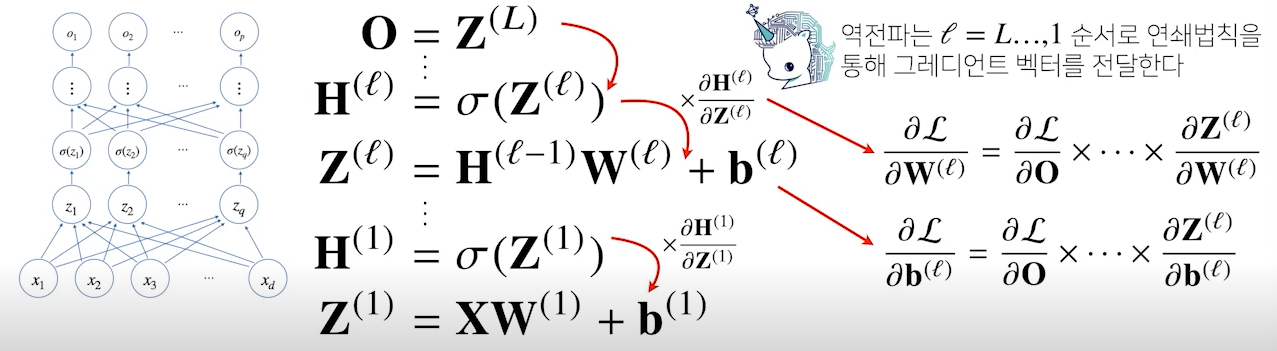
• 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용
• 역전파 알고리즘은 순전파 알고리즘보다 더 많은 메모리를 사용
  • 역전파는 최하층의 미분을 진행하려면 그 위의 모든 노드에 대한 텐서값을 컴퓨터가 가지고 있어야 함

    

2층 신경망

• 다른 예제로 진행항 역전파 (Backpropagation) 계산 : https://pasus.tistory.com/114
• 공부 시 참고했던 행렬 미분 내용 https://datascienceschool.net/02%20mathematics/04.04%20%ED%96%89%EB%A0%AC%EC%9D%98%20%EB%AF%B8%EB%B6%84.html