• 무어펜로즈 역행렬을 사용하지 않고 선형 모델 만들어보기
  • 선형 모델이 아닌 경우에도 적용할수 있는, 조금 더 일반적인 기계 학습 모델에서도 사용하는 방법에 대해 학습

경사하강법

경사하강법으로 선형회귀 계수 구하기

• 선형회귀의 목적은 $||y-X\beta||_2$을 최소화 하는 $\beta$를 찾아야 하므로 다음과 같은 그레디언트 벡터를 계산

  $\nabla_{\beta}||y-X\beta||_2=(\partial_{\beta_1}{||y-X\beta||_2,\cdots,\partial_{\beta_d}{||y-X\beta||_2}})$
  ※ $||y-X\beta||_2$ 대신 $||y-X\beta||^2_2$도 가능

  $\begin{matrix} \partial_{\beta_k}{||y-X\beta||_2} &=& \begin{Bmatrix} {1\over n} \sum_{i=1}^n (y_i - \sum_{j=1}^d X_{ij}\beta_i )^2 \end{Bmatrix}^{1/2} \\ \\ &=& -{{X_k^T(y-X\beta)}\over\ n||y-X\beta||_2} \end{matrix}$
  ※ $X_k^T$ : 행렬 $X$의 $k$번째 열(column)벡터를 전치시킨 것

• 이 공식을 토대로 vector_1 ~ vector_d까지 각각의 gradient vector를 계산

  $\begin{matrix} \nabla_{\beta}{||y-X\beta||_2} &=& (\partial_{\beta_1}{||y-X\beta||_2}, \cdots, \partial_{\beta_k}{||y-X\beta||_d}) \\ \\ &=&(-{{X_1^T(y-X\beta)}\over\ n||y-X\beta||_2}, \cdots, -{{X_d^T(y-X\beta)}\over\ n||y-X\beta||_2}) \\ \\ &=& -{{X^T(y-X\beta)}\over\ n||y-X\beta||_2} \end{matrix}\\$
  ※ 복잡한 계산이지만 실상은 $X\beta$를 계수 $\beta$에 대한 미분한 결과인 $X^T$만 곱해지는 것

-l2-norm의 제곱을 이용하면 조금 더 간결한 식이 나옴

$\begin{matrix} \nabla_{\beta}{||y-X\beta||_2^2} &=& (\partial_{\beta_1}{||y-X\beta||_2^2}, \cdots, \partial_{\beta_k}{||y-X\beta||_d^2}) \\ \\ &=&(-{2\over\ n}{X_1^T(y-X\beta)}, \cdots, -{2\over\ n}{X_d^T(y-X\beta)}) \\ \\ &=& -{2\over\ n}{X^T(y-X\beta)} \end{matrix}\\$

• 목적식을 최소화하는 $\beta$를 구하는 경사하강법 알고리즘은 다음과 같다

  $\beta^{(t+1)} \Longleftarrow \beta^t -\lambda \times\nabla_{\beta}{||y-X\beta||_2}\quad ( or\ \nabla_{\beta}{||y-X\beta||_2^2})$
  ※ 기존 beta - 학습률 x 목적식

경사하강법 기반 선형회귀 알고리즘

# norm : L2 노름을 계산하는 함수
# Input : X, y, lr, epochs(T, 학습획수)
# Output = beta
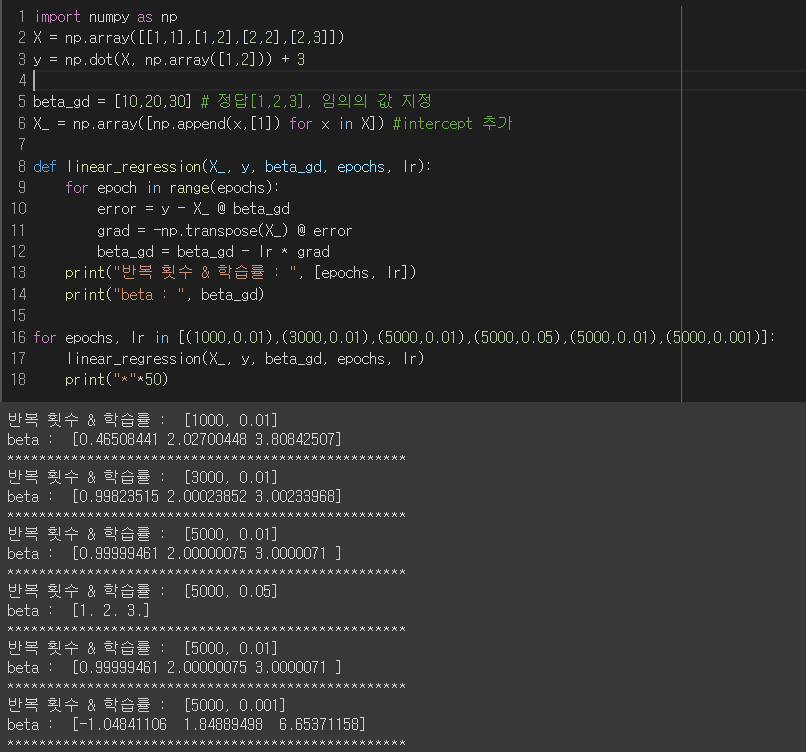
for epoch in range(epochs):
    error = y - X @ beta
    grad = - transpose(X) @ error
    beta = beta - lr * grad

• 무어펜로즈 역행렬로 구한 선형회귀식을 구하는 알고리즘과 차이는 학습 정지 규칙
  • 기존엔 오차 기준이었고, 이번에는 학습 횟수
  • 어느 것을 선택해도 무방함
• 학습을 할 때 적당한 학습 횟수와 학습률을 지정해야 함
• 학습률이 너무 작거나 목표한 값에 도달을 못하고, 너무 크면 불안정함
• 학습 횟수가 너무 적으면 목표한 값에 도달을 못하고, 너무 크면 불필요한 리소스 과다 사용

  

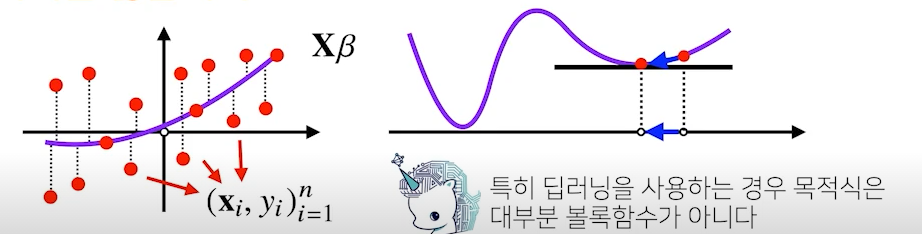
• 경사하강법은 만능은 아니며, 이론적으로 미분가능하고 볼록한 함수에 대해 적절한 학습률과 학습 횟수를 선택했을 때에만 수렴 보장
• 선형 회귀의 경우 볼록한 함수이기에 수렴을 보장
• 단, 비선형회귀 문제는 목적식이 볼록하지 않기에 수렴이 보장되어 있지 않음

  

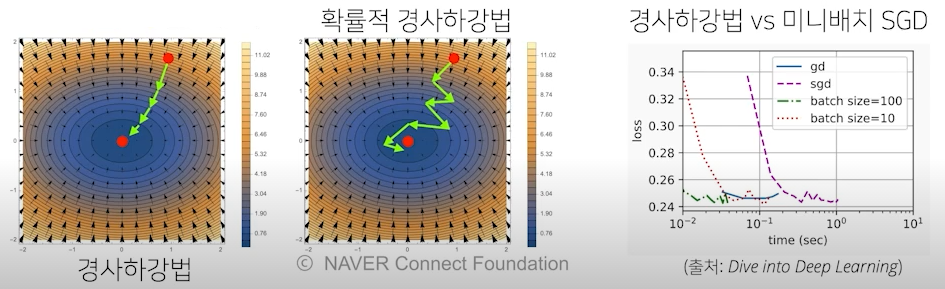
확률적 경사하강법

• 확률적 경사하강법(stochastic gradient descent)은 모든 데이터를 사용해서 업데이트하는 대신 데이터 한 개 또는 일부(mini-batch)를 활용하여 업데이트
• 볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화 가능
• 모든 데이터를 사용한 것이 아니기에 모든 데이터를 사용한 gradient vector와 유사하긴 하지만 같지는 않음, 하지만 SGD의 기댓값이 GD와 유사
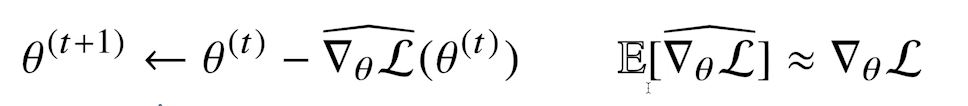
  • SGD도 만능은 아니지만 딥러닝의 경우 SGD가 일반적인 GD보다 실증적으로 낫다고 검증됨

    

• SGD는 데이터의 일부를 가지고 업데이터하기에 연산자원을 조금 더 효율적으로 활용 가능

  

SGD 원리 : 미니배치 연산

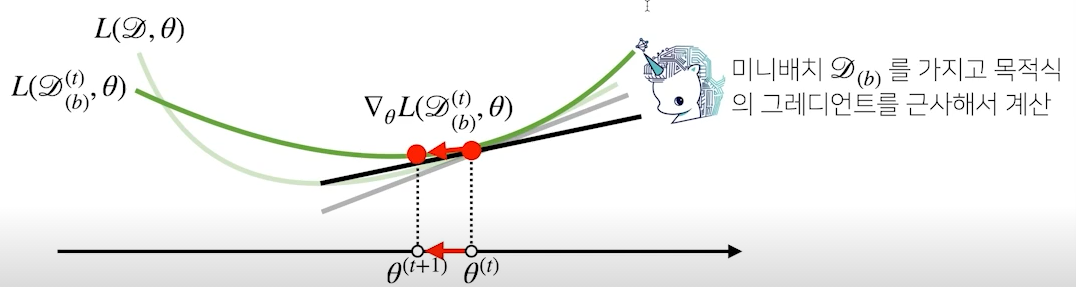
• 경사하강법은 전체 데이터를 $D = (X,y)$를 가지고 목적식의 그레디언트 벡터인 $\nabla_\theta L(D,\theta)$를 계산
• SGD는 미니배치 $D_{(b)} = (X_{(b)},y_{(b)}) \subset D$를 가지고 그레디언트 벡터 $\nabla_{(b)} L(D_{(b)}^{(t)},\theta)$를 계산
  • 목적식의 모양이 미니배치에 따라 달라져서 기본 gradient 벡터와 비슷하지만 다른 여러개의 gradient 벡터를 얻을 수 있음
  • 비선형의 경우 수많은 볼록한 구간이 존재하는데, 경사하강법이 찾은 minimum이 어느 구간의 minimum인지 확인 불가
  • SGD의 경우 mini-batch로 서로 다른 볼록한 구간을 보유했기에 조금 더 정확한 최솟점을 찾을수도 있음
• SGD는 볼록이 아닌 목적식에서도 사용 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적
  • 경사하강법처럼 모든 데이터를 메모리에 업로드하면, 대용량 데이터일 경우 Out-of-memory도 발생
  • sgd로 하면 배치 크기만큼만 업로드하기에 효율적인 메모리 관리 가능

★★★★★ 경사하강법 설명 : https://light-tree.tistory.com/133