조건부 확률

• 데이터가 새로 추가될 때 데이터를 업데이트 하는 방식에 대한 이론적 기반으로, 기계학습에 사용하는 예측 모형의 방법론에 많이 사용됨

베이즈 정리

• 베이즈 통계학을 이해하기 위해선 조건부확률의 개념에 대한 이해가 필요
  • $P(A \cap B) = P(B)P(A|B)$
  • 조건부확률 $P(A|B)$는 사건 B가 일어난 상황에서 사건 A가 발생활 확률
• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법
  • $\textcolor{red}{P(B|A)} = {P(A\cap B) \over P(A)} = \textcolor{red}{P(B)}{P(A|B) \over P(A)}$
  • $A$라는 새로운 정보가 주어졌을 때 $P(B)$로부터 $$P(B|A)$를 계산하는 방법을 제공

베이즈 정리의 용어정리

• Bayesian이란 즉, 사후확률(posterior)을 모델링하는 것으로, 관심있는 대상을 찾는게 아니라 관심 대상의 분포를 찾는 것
  • D : 새로 관찰하는 데이터를 의미
  • $\theta$ : 가설, 모델링하는 이벤트, 모델에서 계산하고자 하는 파라미터(모수) 등 모델링 target 의미
  • 사후확률(posterior) : 데이터가 주어졌을 때 가설이 성립할 확률
  • 사전확률(Prior) : 데이터가 주어지기 전 모델링에 대한 가정을 설정하고 확률분포에 대해 미리 설정해놓은 확률분포
  • 가능도함수 : 설정한 모수 또는 가설이 주어졌을 때 데이터가 관찰될 확률
  • Evidence : 데이터 자체 분포

    

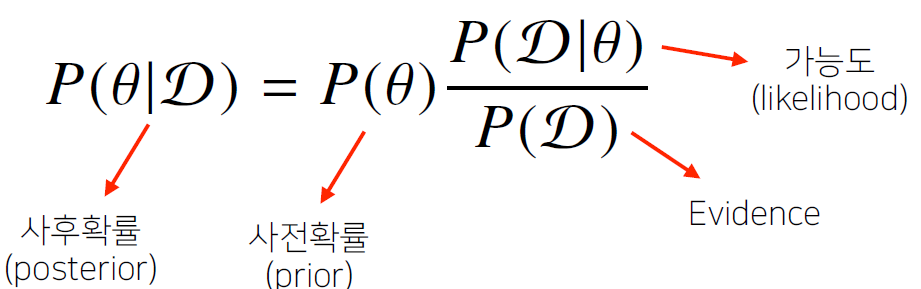
베이즈 정리 예제

• 다음과 같이 사전확률과 가능도를 선정했다면 evidence를 구해야 함
• evidence는 전전체확률정리(법칙)에 의해 구할 수 있음
• evidence 및 사후 확률

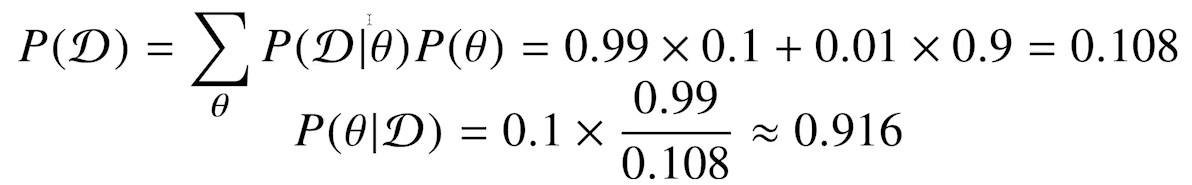
• 만약 오검진율이 1% -> 10%로 증가하면 어떻게 될까?
  • 아래와 같이, 양성반응일 때 실제 걸렸을 확률이 매우 낮아진다.
  • 즉, 오탐율(False alarm)이 오르면 테스트의 정밀도(Precision)이 떨어진다.

조건부 확률 시각화

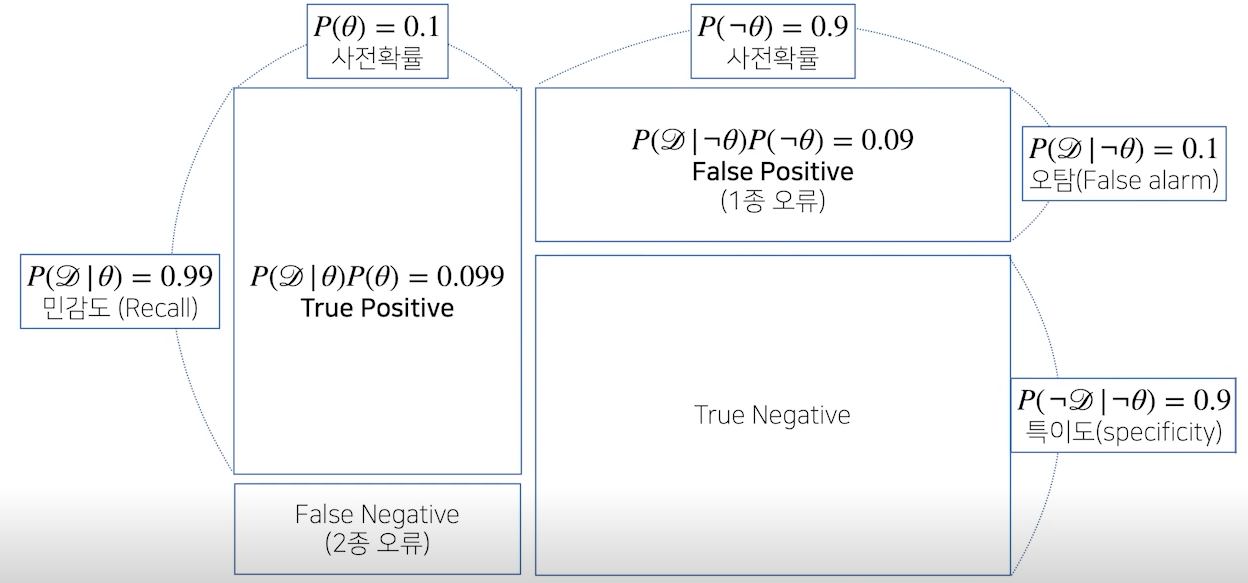
• TP : 양성으로 나왔는데 질병에 걸린 경우
• FP : 양성으로 나왔는데 질병에 걸리지 않은 경우(1종 오류, 오탐)
• FN : 음성으로 나왔는데 질병에 걸린 경우 (2종 오류)
• TF : 음성으로 나왔는데 질병에 걸리지 않은 경우

• 테스트 평가지표(confusion matrix 이용)
  • Recall(민감도, sensitivity) : 참 값 중 참으로 예측한 비율, TP/(TP+FN)
  • Precision(정밀도) : 참으로 예측한 것 중 실제 참인 비율, TP/(TP+FP) => 상기 문제에 오탐율에 따라 정밀도가 매우 크게 변동하는 것을 볼 수 있음
  • 1-특이도(False Positive Rate, FPR) : 거짓 값 중 참으로 예측한 비율
  • accuracy는 잘 활용 안함 => 관심 데이터가 1인데 1의 데이터가 적으면서 0을 잘 맞추는 모델의 경우, 정확도는 높지만 1을 맞춘 비율이 매우 낮을 수도 있음
  • f1-score : recall과 precision의 조화평균

• 1종 오류 및 2종 오류 중 데이터 종류에 따라 관심 오류가 달라짐
  • 암 환자의 경우, 1종 오류보단 걸렸는데 음성으로 나온 것이 더 문제가 됌(의료 문제 : 2종 오류가 중요!!)
  • 반대로 약을 판매하는 경우, 약 효과가 없는데 있다고 한 1종 오류가 문제가 됨(제약, 1종 오류가 중요!!)

베이즈 정리를 통한 정보의 갱신

• 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산가능
• likelihood는 그대로 사용하고, evidence를 다시 구한 다음, 수식에 맞춰서 계산
• 1차에 정밀도가 52.4%밖에 안나왔지만, 2차때는 91.7%까지 검출, 한 번 더 진행하면 99.1%까지 검출!

조건부 확률 $\rightarrow$ 인과관계?

• 조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계(causality)을를 추론할 때 함수로 사용해선 안됨
  • 데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것을 불가
• 인과관계는 데이터 분포의 변화에 간건한 예측모형을 만들 때 필요
• 조건부확률 기반 예측 모형은 테스트 정확도는 매우 높으나 새로운 데이터가 들어올 시 예측정확도가 낮아질 수 있음
• 반대로, 인과관계 기반은 조건부 확률만큼의 테스트 예측은 불가하지만 로버스트한 모형을 만들 수 있음

• 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계싼해야 함
  • 그림 상에선 Z를 제거해야 T를 원인으로 했을 때 결과 R의 인과관계를 알 수 있음
  • 가짜 연관성은 데이터의 유입이 생겼을 떄 예측 모형의 정확도를 떨어뜨리는 요인이 될 수 있음
    • ex) 키가 클수록 지능지수가 높다 => why?
    • 나이라는 중첩요인을 제거하지 않았기 때문