Convolution
- MLP는 각 뉴런들이 선형모델과 활성함수로 연결된 fully-connected layer
- MLP는 i번째 출력값을 얻기 위해 가중치의 i번째 행에 대한 값이 필요
- 반면, 컨볼루션 연산은 고정된 가중치 행렬(커널)이 이동을 하며 출력값을 계산
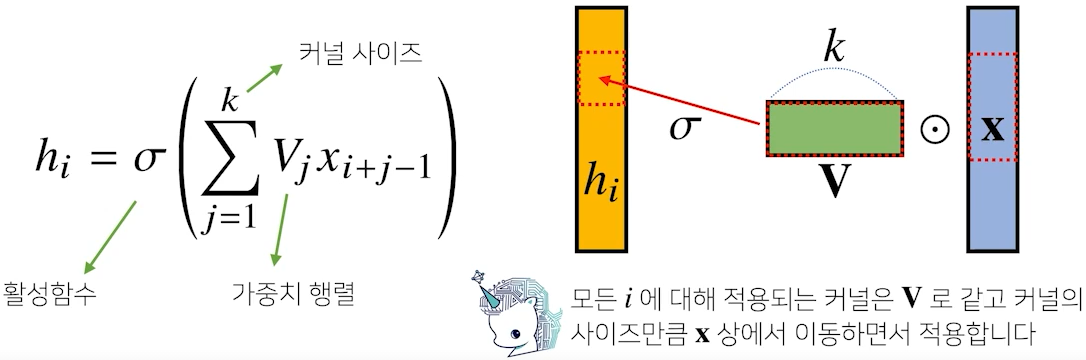
- convolution 연산의 수학적 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것
- Continuous :
- discrete :
- 엄밀히 말하면, 해당 수식에서 대신 를 사용하며, 정확한 용어는 cross-correlation이게 정확함
- 단, 전체 공간에서 plus인지, minus인지 중요하지 않지만, 컴퓨터 내에선 조금 차이가 있음
- 관용적으로 convolution 연산이라고 불렀기에 그대로 부르는 것이며, 실질적으론 다른 연산임을 기억
- 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용
다양한 차원의 Convolution
-
데이터 성격에 따라 사용하는 커널이 달라짐
-
1D-conv
-
2D-conv
-
3D-conv
- 커널은 위치는 이동하더라도 값은 변하지 않음
- f() : 커널, p,q,r은 커널의 위치로, p=1,j=2인 2D의 경우 커널의 (1,2) 위치의 값
- g() : 입력
-
2D-Conv 연산은 커널을 입력벡터 상에서 움직여가며 선형모델과 합성함수가 적용되는 구조
-
입력 크기를 (H,W), 커널 크기를(, ), 출력 크기(,)라 하면 출력크기는 다음과 같음
-
-
- 만약, 28x28 입력, 3x3커널일 때 2D Conv 연산 시 26x26
-
2차원 입력의 채널의 개수만큼 커널 개수도 있어야 함
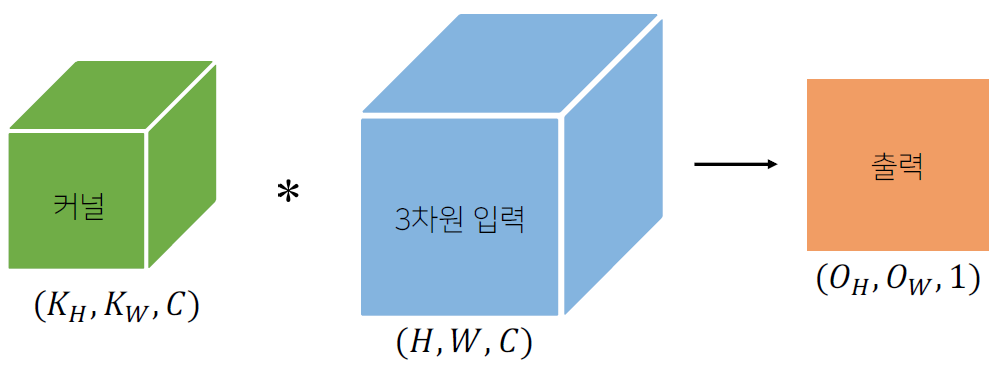
-
만약, 출력을 여러 개 만들고자 한다면 커널을 개 사용하면 출력도 텐서가 됨
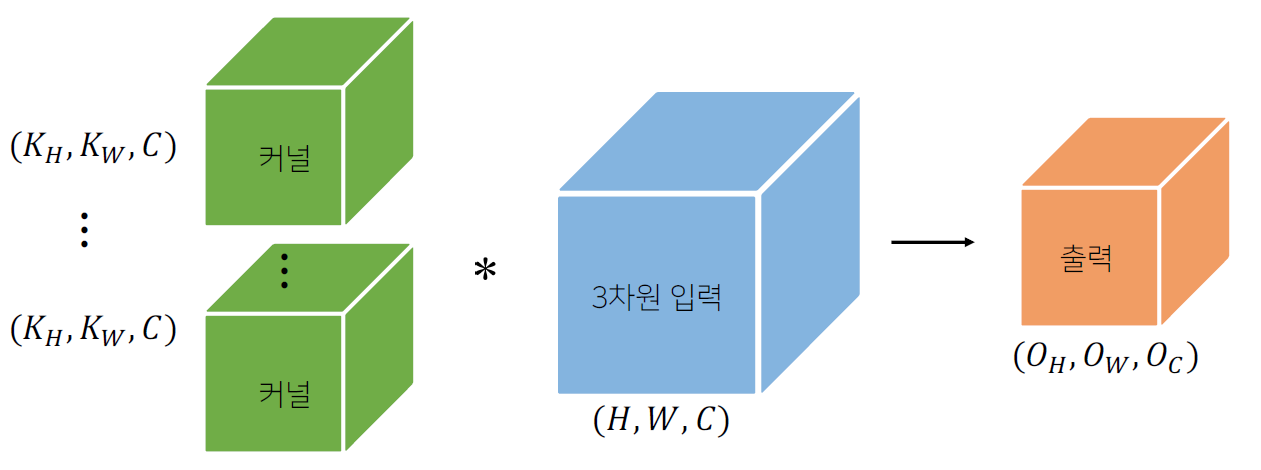
-
Convolution 역전파
- Convolution 연산은 커널이 모든 입력데이터에 대해 공통으로 적용되므로 역전파를 계산할 때도 Convolution 연산 수행
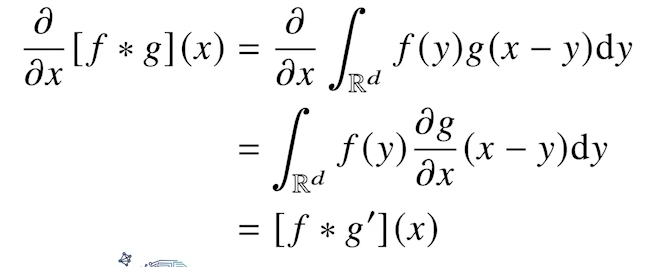
- Discrete일 때도 마찬가지로 성립
-
(순전파)각 입력이 3채널의 커널을 통과하여 출력으로 전달
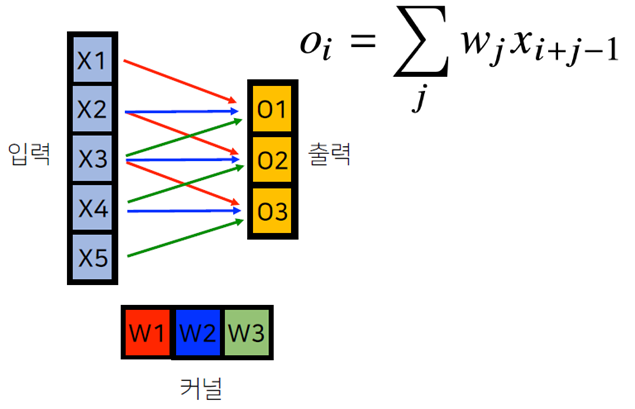
-
(역전파) 각 는 미분값을 의미하며, 순전파 시 각 커널을 통해 입력되었던 것처럼 역전파에서도 동일하게 전달
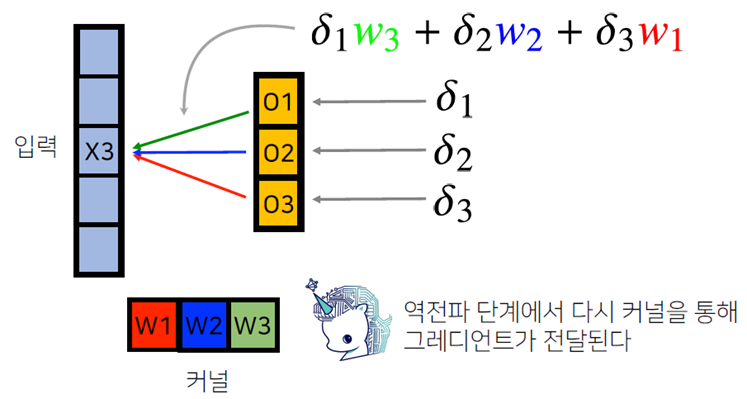
-
이때 커널에는 와 입력 가 곱해져서 전달됨

-
결국 각 커널에 들어오는 gradient를 더해주면 convolution 연산과 동일하다는 것을 알 수 있음

