keywoard

• convex optimization, nonconvex optimization, gradient free optimization

Introduction

• optmization에 대해 공부할 때 다양한 용어의 정의에 대해 제대로 이해하고, 용어를 통일 할 것
• ex) Gradient Desent: 미분함수의 local minimum을 찾기 위해 1차 미분한 값을 이용해 반복적으로 최적화를 시키는 알고리즘

important concpets in Optimization

• Generalization
• Under-fitting vs. over-fitting
• Cross Validation
• Bias-variance tradeoff
• Bootstrapping
• Bagging and boosting

Generalization

• 일반화 성능을 높이는 것
• 일반적으로, 모델이 학습을 할 때 iteration이 반복될수록 train data에 대한 error는 감소
• 하지만, Train Data에 최적화된 모델은 train data에 없는 Test data를 예측할수록 점차 error는 증가
• 따라서 일반화 성능을 높인다는 것은, Test error와 Train error에 대한 gap을 줄이는 것
• 단, 주의할 점은 train data 자체에 noise가 많아서 학습 자체가 잘 이뤄지지 않았을 경우에도 generalization performance는, 즉 Gap은 적을 수 있음

Underfitting vs. Overfitting

• Overfitting : train data에 대한 성능은 좋더라도 test data에 대한 잘 동작하지 않는 현상
• Underfitting : 네트워크가 너무 간단하거나, 학습데이터가 충분하지 않아서 학습 데이터조차 잘 마추지 못하는 현상
• 단, 이 부분들은 이론적이고 실제로 Overfitting과 같은 모델이 target일 수도 있음

  

Cross-Validation(K fold validation)

• model validation technique으로 independent (test) data set에 대한 성능, 즉 Generalization Performance를 높이기 위한 방법
• Train data를 K개의 fold로 나누고 그 중 1개는 train 시 validation data set으로 사용하고 나머지는 train data set으로 활용
  • 단 이때 epoch마다 validation에 사용할 data set이 달라짐(1~k번 중 하나 선택됨)
• Cross validation을 사용하는 경우
  • Data가 충분하지 않아서 validation set을 나눌 수 없을 때
  • neural Net을 학습 시킬 때 많은 하이퍼 파라미터가 존재하는데, 어떤 하이퍼 파라미터가 최적인지 모를 경우 cross validation으로 test를 하고, 이후 최적 파라미터를 선정 후 모든 train data로 학습 진행
    • test data는 절대 학습에 사용되선 안됨

Bias and Variance

• 특정 데이터를 여러 번 예측한 결과를 볼 때, 데이터가 밀집되어 있는 정도를 분산(variance, 정밀도)로 보고, 예측값이 실제값과 근접한 정도를 편향(bias, 정확도)라고 한다.
• 예측 결과가 밀집된 경우, 즉 비슷하게 예측한 경우 => low variance
• 예측한 결과가 target에 근접한 경우 => low bias

Bias ans Variance Tradeoff

• 학습 데이터에 노이즈가 있는 데이터를 minimizing하는 것은 세 가지 파트(bias, variance, noise)로 나뉜다.
• 이 때 loss를 줄이기 위해 각 성분을 minimizing하고 싶으나 하나를 줄이게 되면 다른 하나는 커지는, 즉 tradeoff형태이다.

출처 : https://www.analyticsvidhya.com/blog/2020/08/bias-and-variance-tradeoff-machine-learning/

bootstrapping

• Bootstrapping is any test or metric that uses random sampling with replacement.
• 학습 데이터가 고정되어 있을 때 학습데이터를 일정 비율로 random sampling 하는 방법론

Bagging vs Boosting

• Bagging(Bootstrapping aggregating)
  • multiple models ard being trained with bootstrapping
    • ex) Base classifiers ard fitted on random subset where individual predictions are aggregated(voting or averaging)
  • bootstrapping을 이용한 앙상블
  • bootstrapping 방법을 이용하여 만든 random subset으로 학습한 여러 개의 모델을 생성해내는 방법
  • 입력이 들어온 경우 모델들의 투표(평균 등)을 통해 uncertainty 예측
  • 모든 train 데이터를 활용하여 하나의 모델을 만드는 것보다, 일부 데이터만을 활용하여 여러 개의 모델의 앙상블로 결과를 예측하는게 성능이 더 좋을 때가 많음
• Boosting
  • It focuses on those specific training samples that are hard to classify.
  • A strong model is built by combining weak learners in sequence where each learner learns from the mistakes of the previou sweak learner.
  • sequential한 weak learner들을 여러 개 결합하여 예측 혹은 분류 성능을 높이는 알고리즘[참고]

---

Optimization

Practical Gradient Descent Methods

• Stochastic Gradient Descent(SGD)

  • 한 개의 데이터씩 gradient를 계산하여 weight를 update하는 방법

• Mini-batch Gradient Descent

  • 전체 데이터를 mini-batch로 나누고 mini-batch마다 gradient를 계산하여 weight를 update하는 방법

• Batch Gradient Descent

  • 한번에 전체 데이터의 gradient를 구하여 weight를 update하는 방법

batch size matters

On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima (ICLR 2017) 논문 해석

• batch size를 크게 할 경우 sharp minima로 수렴할 가능성이 높아지고
• batch size를 작게 할 경우 flat minima로 수렴할 가능성이 있음
• 결과적으로 train data에서 잘 동작하면 test data에서도 잘 동작하므로 small batch인 경우 Generalization 성능이 높음

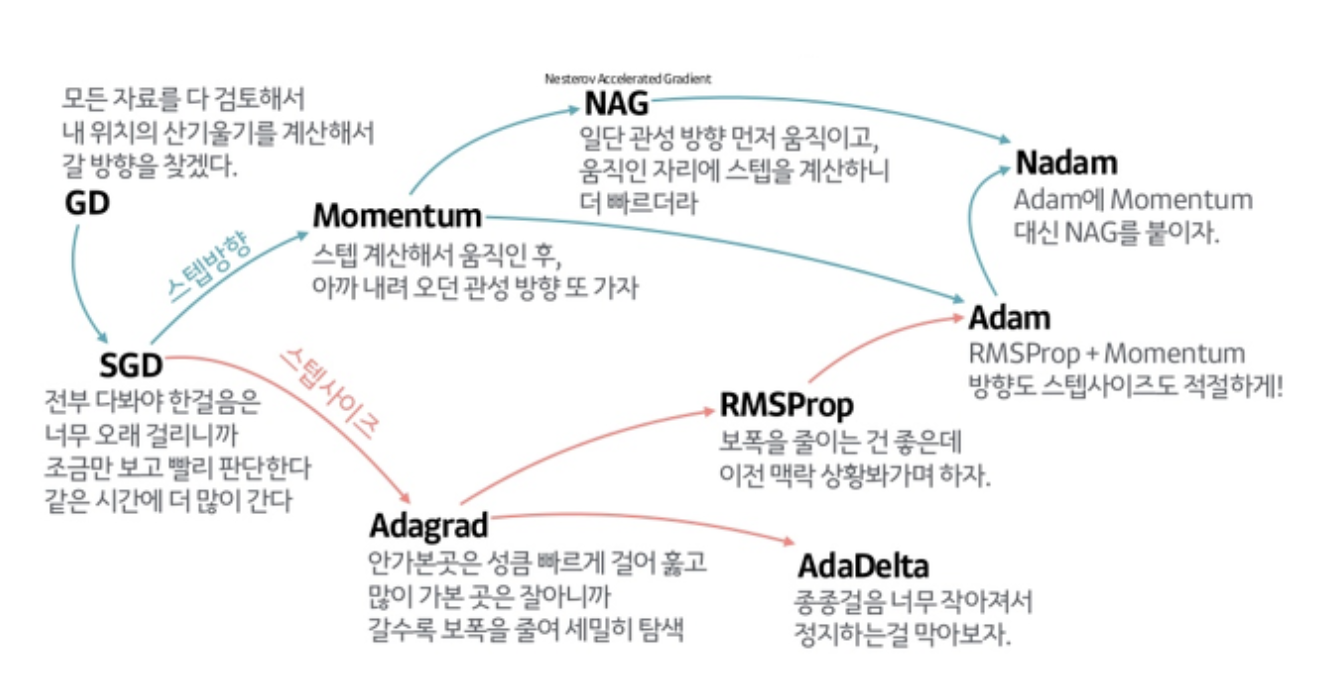
Gradient Descent Methods

• Stochastic gradient descent
• Momentum
• Nesterov accelerated gradient
• Adagrad
• Adadelta
• RMSprop
• Adam

(Stochastic) gradient descent

• gradient를 lr을 곱하여 기존 Weight에서 빼줌
• 단, learning rate(or step size)를 선정하기가 어려움
• 너무 크면 수렴이 안되고, 너무 작으면 시간이 오래 걸림

  

---

• 모델을 학습 시킬 때 objective function를 optimize하는 방법은 다양하게 있는데, 간단한 방법으로는 loss를 최소화 하는것도 optimize의 일종

• 그 중 한가지 방법으로 convex optimization으로 크게 gradient descent method, newton method, lagrange multiplier 구분

gradient descent(batch gradient descent)

• $θ=θ−η∇θJ(θ)$
• 모든 데이터에 대해 gradient를 계산하고, 이 값을 학습률과 곱하여 weight를 update하는 방법
• 문제는, minima로 찾은 point가 global인지, local인지, saddle point인지 확인이 불가
• 또한 전체 데이터를 사용하기에 학습 속도가 매우 느림

  

Stochastic Gradient Descent

• 확률적 경사하강법
• 전체 데이터에서 일부 데이터를 추출하고, 추출된 데이터를 한개씩 학습하여 weight을 update
• 하나의 데이터만으로 gradient를 계산하기에 이전 데이터에선 minima라도 다음 데이터에선 minima가 아닐 수 있음
• 결과적으로, batch gradient descent 대비 속도 개선
• 단, gradient가 매우 크기에 진행 방향이 크게 바뀔 수 있으며, local minima에 수렴학 확률을 줄어들지만 최적해의 정확도는 낮은 편
  

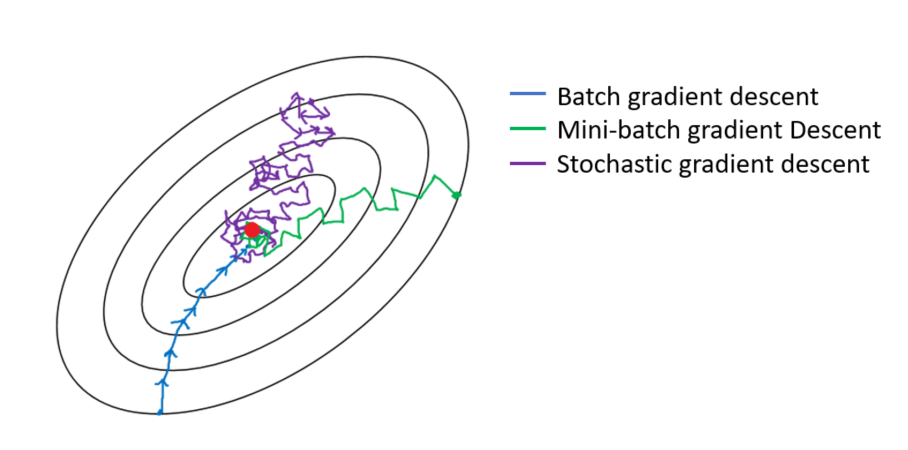
mini-batch Gradient Descent

• 미니배치 경사하강법
• 전체 데이터를 랜덤하게 mini-batch로 나누고, mini-batch로 gradient를 계산하여 weight를 업데이트
• batch gradient descent보다 빠르고, Stochastic Gradient Descent만큼 gradient의 변화가 크지 않음

---

Momentum

• (Stochastic) gradient descent 개선된 optimizers
• mini-batch 별로 데이터가 달라서 batch의 gradient와 다음 batch의 gradient가 다를 경우가 있음
• 이때, Momentum optimizer는 현재의 gradient의 방향성을 다음 gradient에도 활용해보고자 함
• 이것의 장점은 한 번 흘러간 gradient를 어느 정도 유지시켜주기에 gradient가 왔다갔다 하더라도 어느 정도 잘 학습이 진행됨
• 단, gradient가 방향이 바뀐 경우 이전 gradient와 현재 gradient 사이에 local minima가 존재하여 수렴하는 방향으로 이동해야 하는데 momentum 알고리즘에 의해 현재 방향성을 유지하여 local minima 반대 방향으로 더 움직이다가 방향성이 바뀜
• 이러한 과정의 반복으로 인해 local minima로 converging이 어려움
• 이 문제를 개선한 것이 Nesterov Accelerated gradient

  

Nesterov accelerated gradient

• momentum은, 현재 주어진 파라미터에서 gradient를 계산하고, 그 gradient를 가지고 momentum을 accumulation을 진행
• 반면에, Nesterov accelerated gradient는 현재 주어진 파라미터를 가지고 다음 값으로 가서 gradient를 계산하고, 그 상태에서 acculation을 계산하여 weight를 update
• momentum보다 수렴속도가 빠름

Adagrad

• 이전까지는 momentum을 이용한 알고리즘
• 반면에, Adagrad 이후부턴 학습률에 대해 조정해보고자 함
• Adagrad는 parameters의 학습량을 토대로 학습률을 조정하는 알고리즘으로, 많은 변화가 있던 parameters는 학습률을 낮추고, 반대로 학습을 적게 한 parameters는 학습률을 올림
• 이 때 해당 parameter가 얼만큼 변했는지에 대한 값은 $G_t$에 저장됨
  • $G_t$ : sum of gradient squares로, gradient의 변화량을 제곱해서 더함
• adaptive learning rate를 최초로 도입한 optimizers
• 단, 문제는 G가 무한대로 가게 되면 W의 업데이트가 되지 않아 뒤로 갈수록 학습이 점점 멈춰지는 현상이 발생함
• 이것을 해결해보고자 했던 방법론들이 Adadelta, RMSProp

Adadelta

• adagrad의 연장으로, 이론적으로 무한대까지 커지는 G를 막기 위해 가장 간단한 방법은 현재 time step에서 어느 정도 window size만큼의 시간에 대한 gradient 값만 고려
• 단, 이 부분에 문제는 해당 window size만큼 데이터를 갖고 있어야 한다는 점
  • 만약 GPT-3같이 천억개의 파라미터를 가진 모델의 경우 일정 시간대의 gradient 정보를 모두 갖고 있기엔 메모리 비효율적
• 따라서, exponential moving average(EMA, 이동평균)인 $\gamma$를 적용하여 일정 time window만큼의 정보만 고려
• adadelta의 가장 큰 특징은 lr가 없어서 조정할 수 있는 요소가 많이 없어서 잘 활용되지는 않음
• 이거 대신 rmsprop이 많이 사용됐었음

  

RMSprop

• rmsprop는 논문으로 발표된 내용이 아니라 Geoff Hinton이 강의 중 이 방법으로 최적화시키면 잘될거라고 발표한 방법론
• Adadelta와 마찬가지로, gradient squares에 EMA를 적용하여 더하여 분모에 넣고, $\eta$라는 stepsize를 분자에 넣음

  

Adam

• adam은 gradient squares + EMA와 momentum을 같이 활용
• hyper parameter : $\beta_1$(momentum을 얼마나 유지시킬지), $\beta_2$(EMA of gradient squares), $\eta$(stepsize), $\epsilon$(분모가 0이 되지 않도록 해주는 값으로 practical 시 중요)
• weight update항에 들어가는 B_2^t, B_1_t는 unbiased estimator가 되기 위해 수학적으로 증명한 값

  

Regularization

데이터가 제한적일 때 Generalization performance를 높이기 위해 학습을 방해하는 방법론

• Ealry Stopping
• Parameter norm penalty
• Data augmentation
• Noise robustness
• Label smoothing
• Dropout
• Batch normalization

Ealry Stopping

• 학습 시 loss가 어느 시점부터 커지기 시작하는데 그 전에 멈추기 위한 방법

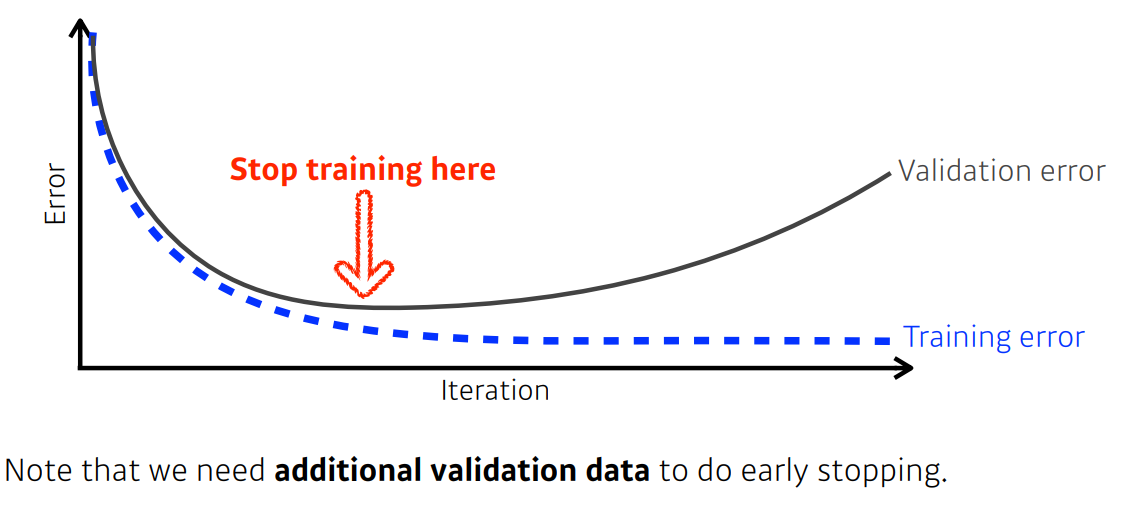
Parameter norm penalty

• Nueral Net이 만든 함수 공간을 최대한 smooth하게 만들면 Generalization performance가 높을 거라는 가정에서 시작
• Nueral Net의 파라미터가 너무 커지지 않게 방지
• network 파라미터들을 다 제곱하여 더한 값을 같이 줄임
• 파라미터 값의 절대값 기준에서 크기 자체를 줄이고자 함
• 이것을 parameter Norm penalty 또는 weight decay라고 함

Data augmentation

• 데이터가 적을 땐 DL 보단 ML이 성능이 더 높을 경우가 많았음
• 반대로 데이터가 많을 땐 Neural Net, Deep learning 성능이 높아짐
• 데이터를 증량시키는 방법 다양한 방법이 있음

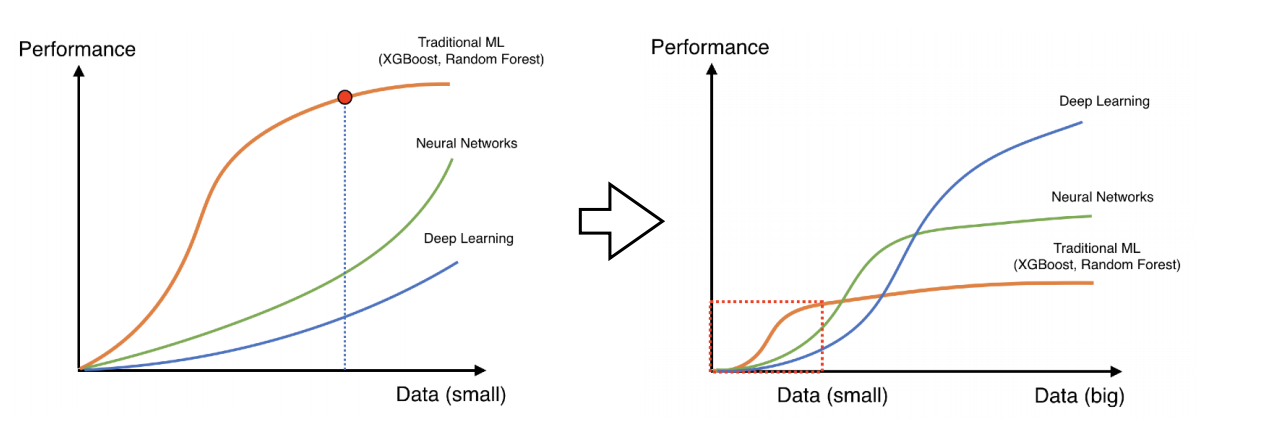
• 그 중 한 가지로, 이미지 데이터의 경우 데이터를 특정 각도로 틀어도 동일한 이미지인데, 이런 식으로 데이터를 증량시키는 방법을 label preserving agmentation(label이 바뀌지 않는 한도 내에서 데이터를 변환하여 증량시키는 방법)
• 이미지에서도 mnist의 경우는 뒤짚거나 하는 변환을 하면 label이 바뀌기에 하면 안됨

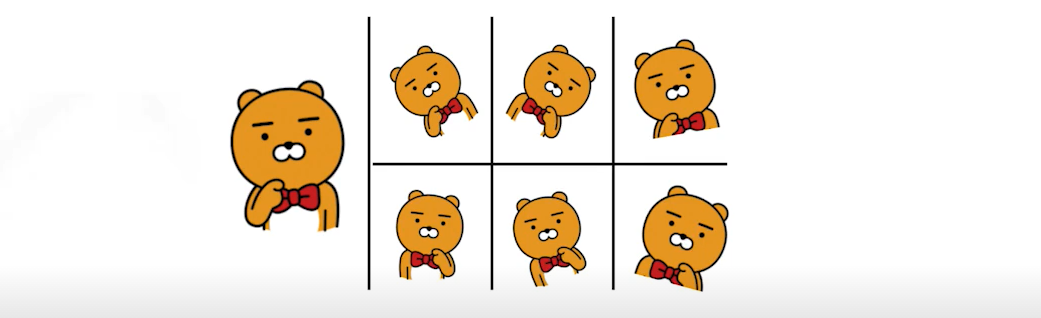
Noise robustness

• 입력 및 weight에 random noises를 집어넣는 방법

Label smoothing

• data augmentation과 유사하나
• Label smoothing 효과 : 예로, 이미지 분류 문제에서 image data set 안에서 특정 class들을 구분지을 수 있는 decision boundary를 찾고하는 경우
• 해당 regularization을 통해 generalization performance가 향상됨
• Label smoothing : mix-up과 cutMix, cutout 등이 존재
  • Mix-up : train data 두개를 섞어서 합쳐주는 방법
  • cutMix : 두 개의 데이터의 일부 영역을 cut 후 cut된 부분을 바꿔주는 방법

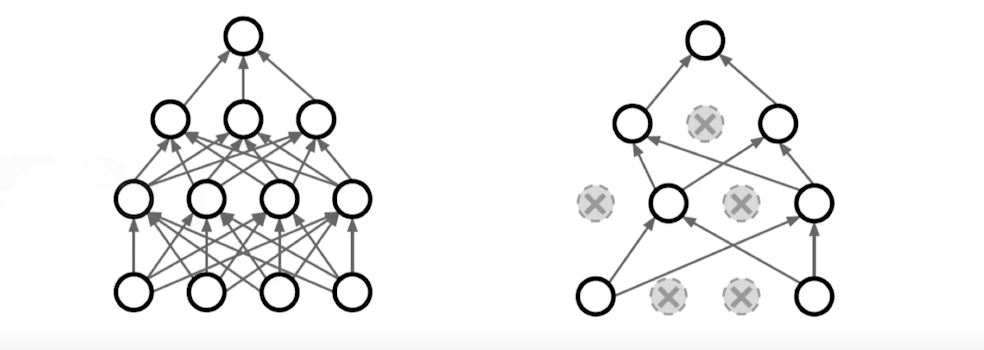
Dropout

• NeurNet의 weight를 지정한 ratio만큼 random하게 0으로 바꾸는 방법
• 각각의 neuron들을 조금 더 robust한 feature로 만들어주기 위한 방법

Batch normalization

• BN을 적용하고자 하는 layer의 statistics를 정규화 시키는 것
  • 예로, 특정 layer에 parameter가 1000개가 있고 100정도의 값을 가지고 있을 때 표준화를 통해 평균=0, 분산=1로 만드는 방법
• 일반적으로, 특히 layer가 깊을수록 해당 방법을 사용하게 되면 performance가 향상됨참고

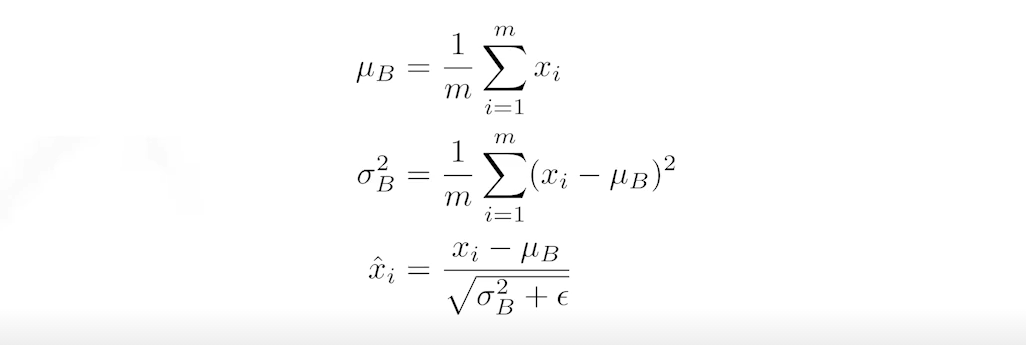
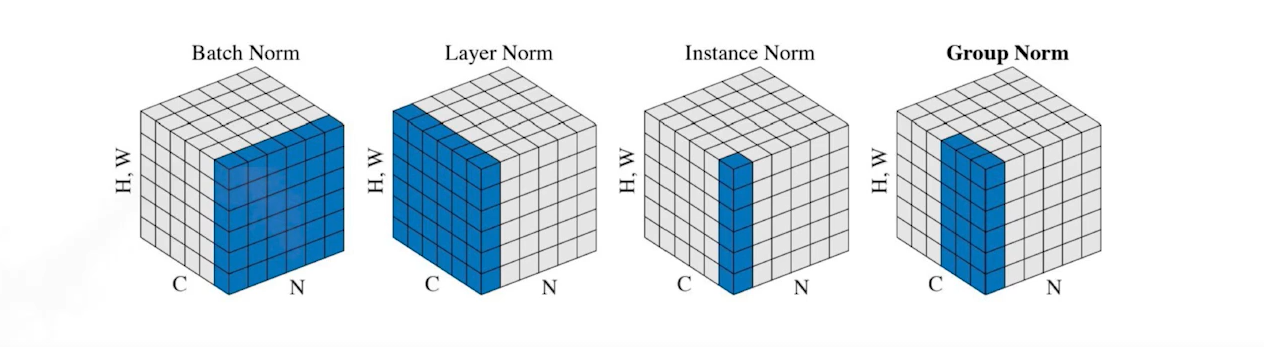
• 다음과 같이 다양한 normalizaiton이 존재
  • batch norm : layer 전체를 줄임
  • layer norm : 각 layer만 줄임
  • instance norm : data instance(이미지의 데이터의 경우 이미지한 장)씩 활용해서 줄임
  • group norm : layer norm과 instance norm의 중간(group normalization 논문 읽어보기 추천!)
• 각 normalization마다 성능이 올라가는 상황이 다르기에 알아두면 좋음

---

참고 자료

• convex optimization
• 딥러닝 옵티마이저(optimizer) 총정리
• 옵티마이저 총정리2, cs231
• 옵티마이저 총정리3
• 옵티마이저 총정리4, 코드로 설명
• 옵티마이저 총정리5
• adabelief
• gd, rmsprop, adam 하드 코딩