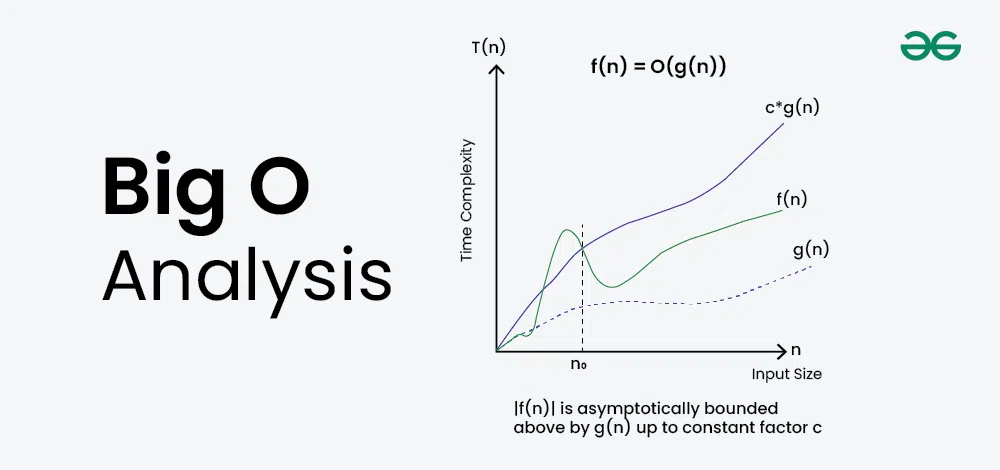
빅오 표기법에 대한 내용은 전 게시물에 작성해두었다. 참고하자!
빅오 표기법의 성능 순서
빅오 표기법의 성능 순서는 다음과 같이 나타낼 수 있다.

- 가장 왼쪽
O(1)으로 갈수록 실행 횟수가 적은 것 / 시간 복잡도가 낮은 것 - 가장 오른쪽
O(n!)으로 갈수록 실행 횟수가 많은 것 / 시간 복잡도가 높은 것
O(1) - 상수 시간 복잡도
이 시간 복잡도는 입력 크기와 무관하게 항상 일정한 실행 시간을 가진다.
예제 코드:
def constant_time_example(lst):
return lst[0]설명:
이 함수는 리스트 lst의 첫 번째 요소를 반환한다. 리스트의 크기가 얼마나 크든 상관없이 첫 번째 요소에 접근하는 작업은 항상 일정한 시간(O(1))이 소요된다.
O(log n) - 로그 시간 복잡도
입력 크기가 증가함에 따라 실행 시간이 로그 함수의 비율로 증가한다.
예제 코드:
def logarithmic_time_example(n):
i = 1
while i < n:
print(i)
i = i * 2설명:
이 함수는 1부터 시작하여 지수적으로 증가하는 수열을 출력한다. i가 n보다 작을 때까지 두 배씩 증가하므로, 실행 횟수는 입력 n에 대해 로그 시간 복잡도인 O(log n)이다.
O(n) - 선형 시간 복잡도
입력 크기에 비례하여 실행 시간이 증가한다.
예제 코드:
def linear_time_example(lst):
for item in lst:
print(item)설명:
이 함수는 리스트 lst의 각 요소를 한 번씩 출력한다. 리스트의 길이 n에 비례하여 n번 반복하므로, 시간 복잡도는 O(n)이다.
O(n log n) - 선형 로그 시간 복잡도
입력 크기 n에 대해 n과 로그 함수의 곱으로 실행 시간이 증가한다.
예제 코드:
def n_log_n_example(lst):
lst.sort() # 정렬은 O(n log n)
for item in lst:
print(item)설명:
이 함수는 리스트 lst를 정렬한 후 모든 요소를 출력한다. 리스트 정렬은 평균적으로 O(n log n) 시간 복잡도를 가진다. 따라서 정렬 후에 각 요소를 출력하는 데는 O(n) 시간이 걸리므로 전체 시간 복잡도는 O(n log n)이다.
O(n²) - 제곱 시간 복잡도
입력 크기의 제곱에 비례하여 실행 시간이 증가한다.
예제 코드:
def quadratic_time_example(lst):
for i in lst:
for j in lst:
print(i, j)설명:
이 함수는 리스트 lst의 모든 요소 쌍을 출력한다. 이중 반복문을 사용하므로 리스트의 길이 n에 대해 제곱 시간 복잡도인 O(n²)을 가진다.
O(2ⁿ) - 지수 시간 복잡도
각 단계마다 실행 시간이 배로 증가한다.
예제 코드:
def exponential_time_example(n):
if n <= 0:
return 1
else:
return exponential_time_example(n - 1) + exponential_time_example(n - 2)설명:
이 함수는 피보나치 수열을 재귀적으로 계산한다. 각 호출은 이전 두 개의 호출을 추가로 호출하므로 실행 시간이 지수적으로 증가한다. 따라서 시간 복잡도는 O(2ⁿ)이다.
O(n!) - 팩토리얼 시간 복잡도
입력 크기의 팩토리얼에 비례하여 실행 시간이 증가한다.
예제 코드:
def factorial_time_example(n):
if n <= 1:
return 1
else:
return n * factorial_time_example(n - 1)설명:
이 함수는 입력 값 n의 팩토리얼을 계산한다. 재귀적으로 호출하여 n부터 1까지의 모든 수를 곱하는 방식으로 작동하므로 시간 복잡도는 O(n!)이다. 팩토리얼 함수의 실행 시간은 입력 값 n의 증가에 따라 기하급수적으로 증가한다.
결론
이렇게 각각의 빅오 표기법에 대해 예제와 함께 설명해 보았다. 각 시간 복잡도는 알고리즘의 성능을 분석하고 비교하는 데 중요한 지표이니 꼭 이해하고 넘어가도록 하자!
