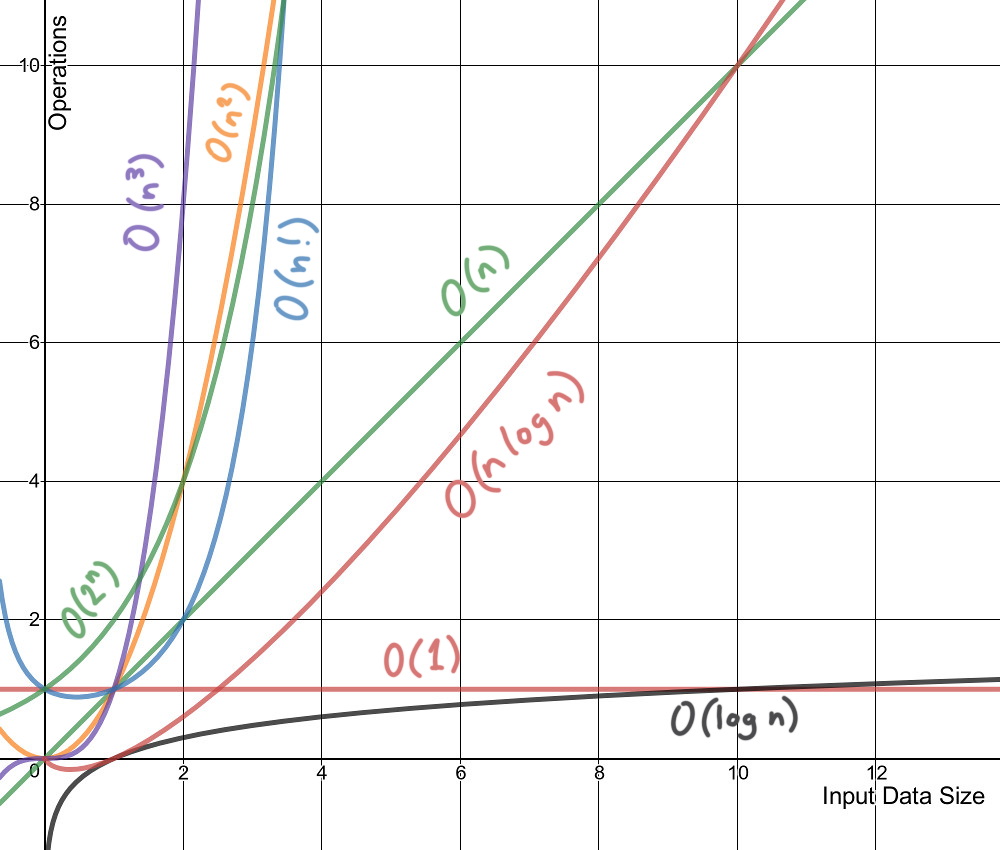
시간 복잡도 예제 10문제
지금까지 시간 복잡도와 빅오 표기법(Big O)에 대해 배워보았다. 이제 간단한 파이썬 코드 문제를 통해 그동안 배운 것들을 잘 기억하고 있는지 테스트해 보자!
시간 복잡도 추정 문제
문제 1
def example1(lst):
print(lst[0])문제 2
def example2(lst):
for item in lst:
print(item)문제 3
def example3(n):
i = 1
while i < n:
print(i)
i = i * 2문제 4
def example4(lst):
n = len(lst)
for i in range(n):
for j in range(n):
print(lst[i], lst[j])문제 5
def example5(n):
if n <= 1:
return 1
else:
return n * example5(n - 1)문제 6
def example6(lst):
lst.sort()
for item in lst:
print(item)문제 7
def example7(n):
i = 0
while i < n:
j = 0
while j < n:
print(i, j)
j += 1
i += 1문제 8
def example8(n):
for i in range(n):
j = 1
while j < n:
print(i, j)
j = j * 2문제 9
def example9(lst):
for i in range(len(lst)):
print(lst[i])문제 10
def example10(lst):
for i in range(len(lst)):
for j in range(len(lst)):
print(lst[i], lst[j])정답과 해설
아래에 각 문제에 대한 정답과 코드 예제를 함께 정리해 두었다.
문제 1 - O(1)
def example1(lst):
print(lst[0])해설: 이 함수는 리스트 lst의 첫 번째 요소를 출력한다. 리스트에서 한 번의 접근만 하므로 실행 시간은 입력 크기와 무관하게 항상 일정하다. 따라서 시간 복잡도는 O(1)이다.
문제 2 - O(n)
def example2(lst):
for item in lst:
print(item)해설: 이 함수는 리스트 lst의 모든 요소를 한 번씩 출력한다. 리스트의 길이에 비례하여 반복하므로 실행 시간은 입력 크기 n에 비례한다. 따라서 시간 복잡도는 O(n)이다.
문제 3 - O(log n)
def example3(n):
i = 1
while i < n:
print(i)
i = i * 2해설: 이 함수는 1부터 시작하여 i를 2배씩 증가시키며 n보다 작을 때까지 출력한다. i의 값이 지수적으로 증가하므로 실행 시간은 입력 크기 n에 대해 로그 함수의 비율로 증가한다. 따라서 시간 복잡도는 O(log n)이다.
문제 4 - O(n^2)
def example4(lst):
for i in range(len(lst)):
for j in range(len(lst)):
print(i, j)해설: 이 함수는 리스트 lst의 모든 요소 쌍을 출력한다. 이중 반복문을 사용하여 모든 요소를 비교하므로 실행 시간은 입력 크기 n에 대해 제곱 비율로 증가한다. 따라서 시간 복잡도는 O(n^2)이다.
문제 5 - O(n!)
def example5(n):
if n <= 1:
return 1
else:
return n * example5(n - 1)해설: 이 함수는 팩토리얼을 계산하는 재귀 함수로, 모든 가능한 순열의 수를 계산한다. 실행 시간은 입력 크기 n에 대해 팩토리얼 비율로 급격히 증가하므로 시간 복잡도는 O(n!)이다.
문제 6 - O(n log n)
def example6(lst):
lst.sort()
for item in lst:
print(item)해설: 이 함수는 리스트 lst를 정렬한 후 모든 요소를 출력한다. 정렬 알고리즘의 시간 복잡도가 O(n log n)이므로 전체 시간 복잡도도 O(n log n)이다.
문제 7 - O(n^2)
def example7(n):
for i in range(n):
for j in range(1, n):
print(i, j)해설: 이 함수는 이중 반복문을 사용하여 모든 요소 쌍을 출력한다. 따라서 실행 시간은 입력 크기 n에 대해 제곱 비율로 증가하므로 시간 복잡도는 O(n^2)이다.
문제 8 - O(n log n)
def example8(n):
i = n
while i > 0:
for j in range(n):
print(i, j)
i = i // 2해설: 이 함수는 i를 절반으로 나누어가며 이중 반복문을 실행한다. 바깥쪽 반복문은 O(log n)이고 내부 반복문은 O(n)이므로 전체 시간 복잡도는 O(n log n)이다.
문제 9 - O(n)
def example9(n):
for i in range(1, n, 2):
print(i)해설: 이 함수는 홀수 인덱스만 출력하는 반복문을 사용한다. 실행 시간은 입력 크기 n에 비례하므로 시간 복잡도는 O(n)이다.
문제 10 - O(n^2)
def example10(n):
for i in range(n):
for j in range(i, n):
print(i, j)해설: 이 함수는 이중 반복문을 사용하여 삼각형 모양으로 모든 요소를 출력한다. 실행 시간은 입력 크기 n에 대해 제곱 비율로 증가하므로 시간 복잡도는 O(n^2)이다.
지금은 간단한 코드지만 기본을 확실하게 다져야 나중에 복잡한 코드를 보고도 계산할 줄 알게 될 것이다. 앞으로도 열심히 공부하자!
