
최단 경로 알고리즘이란?
최단 경로shortest path는 그래프 내의 두 노드 사이의 최단 경로를 찾는 데 사용되는 알고리즘이다. 주로 다음과 같은 두 가지 유형의 그래프에서 적용된다.
1) 가중치 없는 그래프 (Unweighted Graphs):
- 간선 개수가 가장 적은 경로
BFS를 사용하여 최단 경로를 찾음
2) 가중치 있는 그래프 (Weighted Graphs):
- 시작 노드에서 끝 노드까지 거치는 간선의 가중치의 총합이 최소가 되는 경로
- 다익스트라 알고리즘 (
Dijkstra's Algorithm) - 벨만-포드 알고리즘 (
Bellman-Ford Algorithm)
다익스트라 알고리즘 (Dijkstra's Algorithm)
다익스트라 알고리즘은 1959년 에츠허르 데이크스트라가 발표한 최단 경로 알고리즘으로, 사실상 가중치가 있는 그래프의 최단 경로 문제는 대부분 다익스트라 알고리즘을 사용한다고 보면 될 정도로 중요한 알고리즘이다.
🔄️ 동작 단계
- 출발 노드와 도착 노드를 설정한다.
- '최단 거리 테이블'을 초기화한다. 이 테이블은 출발 노드에서 각 노드까지의 최단 거리를 저장한다. 출발 노드의 거리는 0으로, 나머지 노드의 거리는 무한대(∞)로 초기화한다.
- 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다.
- 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트한다.
- 3번과 4번 과정을 반복한다. 모든 노드를 방문할 때까지 반복한다.
🗒️ 용어 설명
-
최단 거리 테이블: 각 노드까지의 최단 거리를 기록한 배열
- N개(1부터 시작하는 노드 번호와 일치시키려면 N + 1개) 크기
- 출발 노드는 0으로, 나머지 노드는 무한대(∞)로 초기화
-
노드 방문 여부 체크 배열: 각 노드가 방문되었는지를 기록한 배열
- 크기는 최단 거리 테이블과 같음
- 기본적으로는
False로 초기화
💻 다익스트라 알고리즘의 예시
간단한 그래프를 통해 다익스트라 알고리즘을 설명하도록 하겠다.
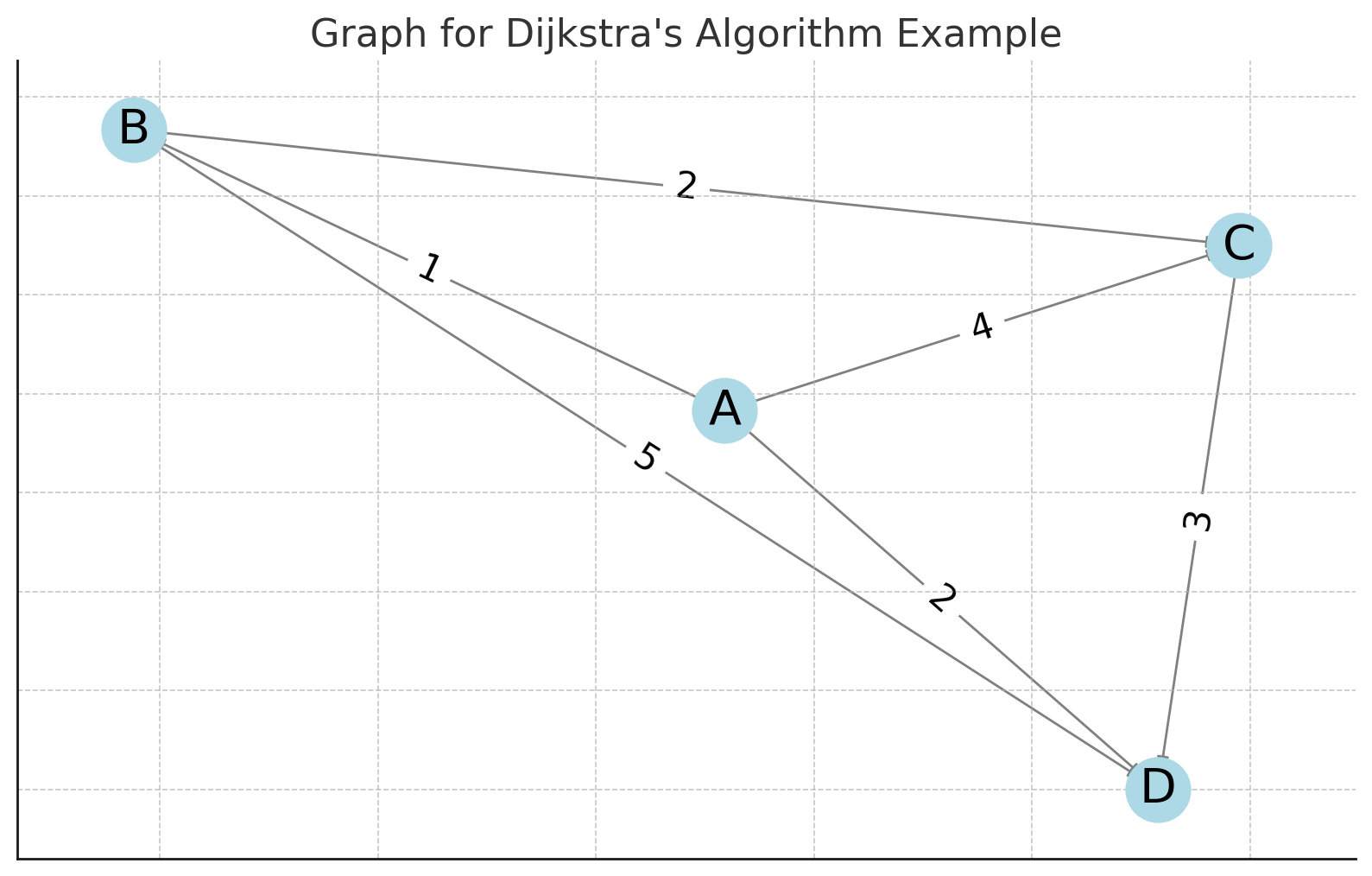
-
출발 노드와 도착 노드 설정
- 출발 노드: A
- 도착 노드: 모든 노드
-
최단 거리 테이블 초기화
- A: 0 (출발 노드)
- B: ∞
- C: ∞
- D: ∞
-
첫 번째 반복 (노드 A에서 시작)
- A -> B (거리 1)
- B까지의 거리는 0 + 1 = 1
- A -> C (거리 4)
- C까지의 거리는 0 + 4 = 4
- A -> D (거리 2)
- D까지의 거리는 0 + 2 = 2
- 최단 거리 테이블 업데이트:
- A: 0
- B: 1
- C: 4
- D: 2
- 노드 방문 여부 체크: A 방문 완료
- A -> B (거리 1)
-
두 번째 반복 (노드 B에서 시작)
- 현재까지의 최단 거리: B (1)
- B -> A (이미 방문한 노드)
- B -> C (거리 2)
- C까지의 새로운 거리: 1 + 2 = 3 (기존 4보다 작음, 갱신)
- B -> D (거리 5)
- D까지의 새로운 거리: 1 + 5 = 6 (기존 2보다 큼, 무시)
- 최단 거리 테이블:
- A: 0
- B: 1
- C: 3
- D: 2
- 노드 방문 여부 체크: A, B 방문 완료
-
세 번째 반복 (노드 D에서 시작)
- 현재까지의 최단 거리: D (2)
- D -> A (이미 방문한 노드)
- D -> B (이미 방문한 노드)
- D -> C (거리 3)
- C까지의 새로운 거리: 2 + 3 = 5 (기존 3보다 큼, 무시)
- 최단 거리 테이블:
- A: 0
- B: 1
- C: 3
- D: 2
- 노드 방문 여부 체크: A, B, D 방문 완료
-
네 번째 반복 (노드 C에서 시작)
- 현재까지의 최단 거리: C (3)
- C -> A (이미 방문한 노드)
- C -> B (이미 방문한 노드)
- C -> D (이미 방문한 노드)
- 최단 거리 테이블 업데이트:
- A: 0
- B: 1
- C: 3
- D: 2
- 노드 방문 여부 체크: A, B, C, D 방문 완료
-
모든 노드를 방문했으니 알고리즘 종료
최종 최단 거리 테이블
- A: 0
- B: 1
- C: 3
- D: 2
🚨 주의점
💡 “음의 가중치가 있는 그래프에서 다익스트라 알고리즘은 어떨까?”
결론부터 말하면 다익스트라 알고리즘은 양의 가중치만 있는 그래프에서만 동작하므로 음의 가중치가 있는 그래프에서 제대로 동작하지 않는다. 그럼에도 다익스트라 알고리즘을 많이 사용하는 이유는 대부분의 경우 음의 가중치를 갖는 경우가 없고, 성능이 매우 뛰어나기 때문이다.
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
벨만 포드 알고리즘 역시 노드에서 노드까지의 최소 비용을 구하는 알고리즘이다. 하지만 벨만-포드 알고리즘은 매 단계마다 모든 간선의 가중치를 다시 확인하여 치소 비용을 갱신하므로 음의 가중치를 가지는 그래프에서도 최단 경로를 구할 수 있다.
🔄️ 동작 단계
- 초기화
- 출발 노드의 거리를 0으로 설정한다.
- 나머지 모든 노드의 거리는 무한대로 설정한다.
- 각 노드의 직전 노드를 None으로 설정한다.
- 간선 완화(Relaxation)
- 모든 간선에 대해 다음 작업을 수행한다.
- 만약 경로의 시작 노드까지의 거리가 무한대가 아니고, 경로의 시작 노드를 거쳐서 가는 것이 더 짧다면, 거리를 갱신한다.
- 이 작업을 그래프의 노드 수 - 1번 반복한다.
- 음의 사이클 체크
- 모든 간선을 한 번 더 검사하여, 만약 경로의 시작 노드를 거쳐서 가는 것이 더 짧다면, 음의 사이클이 존재한다고 판단한다.
💻 벨만-포드 알고리즘의 예시
이번에도 간단한 그래프를 통해 단계를 설명해 보도록 하겠다.
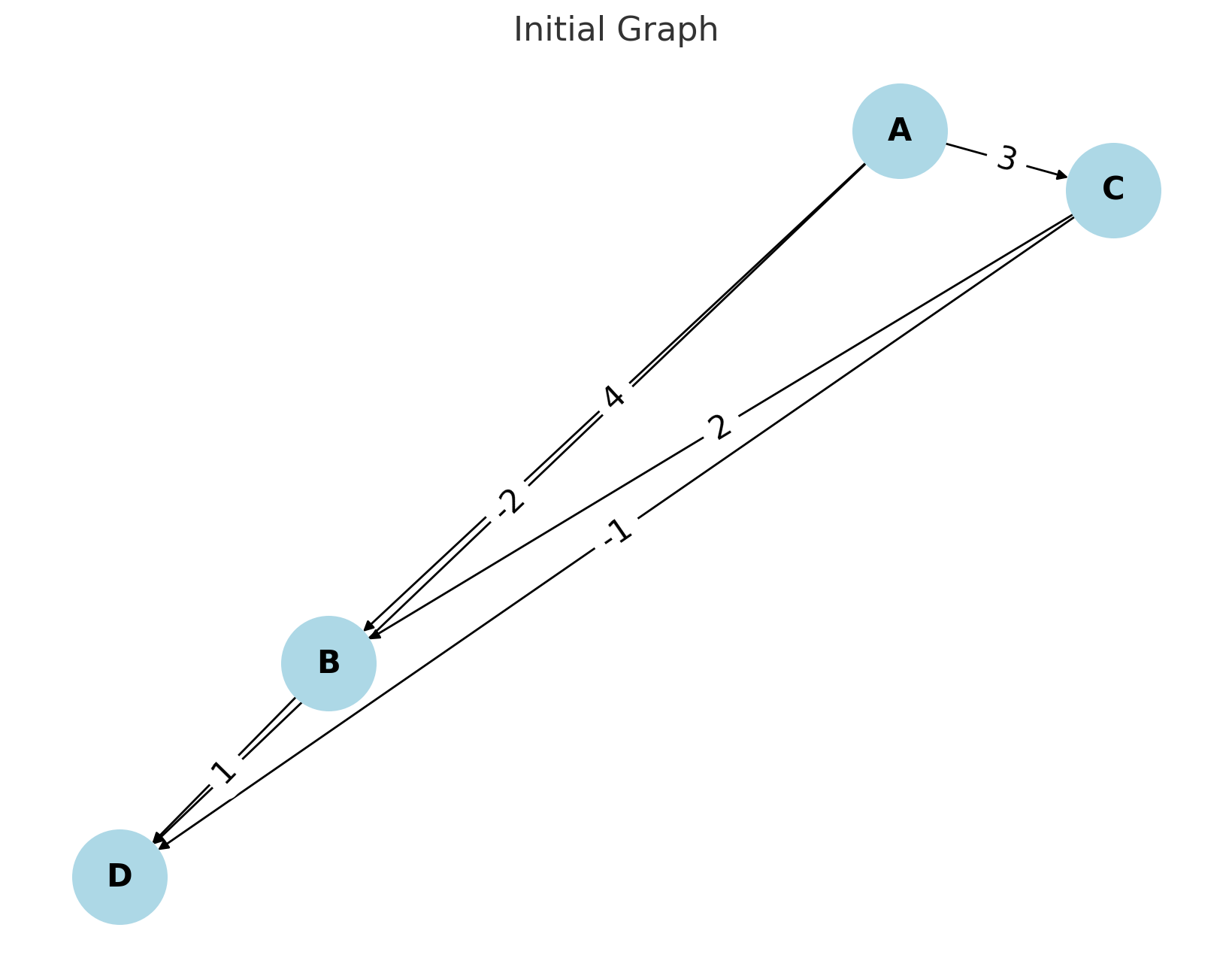
그래프 설명
- 노드와 간선
- A -> B: 4
- A -> C: 3
- A -> D: -2
- B -> C: 2
- B -> D: 1
- C -> D: -1
1. 출발 노드와 도착 노드 설정
- 출발 노드: A
- 도착 노드: 모든 노드
2. 최단 거리 테이블 초기화
- A: 0 (출발 노드)
- B: ∞
- C: ∞
- D: ∞
3. 첫 번째 반복
- 간선 완화:
- A -> B (거리 4): B까지의 거리는 0 + 4 = 4
- A -> C (거리 3): C까지의 거리는 0 + 3 = 3
- A -> D (거리 -2): D까지의 거리는 0 + (-2) = -2
- 최단 거리 테이블 업데이트:
- A: 0
- B: 4
- C: 3
- D: -2
4. 두 번째 반복
- 간선 완화:
- B -> C (거리 2): C까지의 새로운 거리: 4 + 2 = 6 (기존 3보다 큼, 무시)
- B -> D (거리 1): D까지의 새로운 거리: 4 + 1 = 5 (기존 -2보다 큼, 무시)
- C -> D (거리 -1): D까지의 새로운 거리: 3 + (-1) = 2 (기존 -2보다 큼, 무시)
- 최단 거리 테이블 업데이트:
- A: 0
- B: 4
- C: 3
- D: -2
5. 세 번째 반복
- 간선 완화:
- 모든 간선에 대해 더 이상 갱신할 거리 없음
- 최단 거리 테이블 업데이트:
- A: 0
- B: 4
- C: 3
- D: -2
6. 네 번째 반복
- 간선 완화:
- 모든 간선에 대해 더 이상 갱신할 거리 없음
- 최단 거리 테이블 업데이트:
- A: 0
- B: 4
- C: 3
- D: -2
7. 모든 노드를 방문했으니 알고리즘 종료
최종 최단 거리 테이블
- A: 0
- B: 4
- C: 3
- D: -2
🚨 주의점
💡 벨만-포드 알고리즘은 다익스트라 알고리즘보다 느리다?
다익스트라 알고리즘은 최단 경로를 찾기 위해 각 단계마다 가장 짧은 경로를 선택해 나가기 때문에 일반적으로 시간 복잡도가 더 낮다. 반면에 벨만-포드 알고리즘은 모든 가능한 간선을 반복적으로 검사하면서 최단 경로를 찾기 때문에 시간 복잡도가 상대적으로 높다.
마치며
| 특성 | 다익스트라 알고리즘 | 벨만-포드 알고리즘 |
|---|---|---|
| 사용 가능한 그래프 유형 | 양의 가중치만 있는 그래프 | 음수 가중치가 있는 그래프도 처리 가능 |
| 동작 방식 | 각 단계마다 가장 짧은 경로 선택 | 모든 간선을 반복적으로 검사 |
| 시간 복잡도 | 상대적으로 낮음 | 상대적으로 높음 |
| 최단 경로 길이 | 단일 출발점에서 모든 다른 정점까지 최단 경로 계산 | 단일 출발점에서 모든 다른 정점까지 최단 경로 계산 |
| 사용 사례 | 양수 가중치만 있고 시간 복잡도가 중요할 때 | 음수 가중치가 있는 경우의 최단 경로 탐색 |
결론적으로 두 알고리즘은 사용 가능한 그래프 유형과 시간 복잡도 측면에서 차이가 있다. 따라서 경로 탐색에서 시간 복잡도가 중요한 경우에는 일반적으로 다익스트라 알고리즘을, 음수 가중치가 있는 경우나 더 유연한 해결 방법이 필요한 경우에는 벨만-포드 알고리즘이 사용하는편이 좋다.
