📈 그래프(Graph)란?

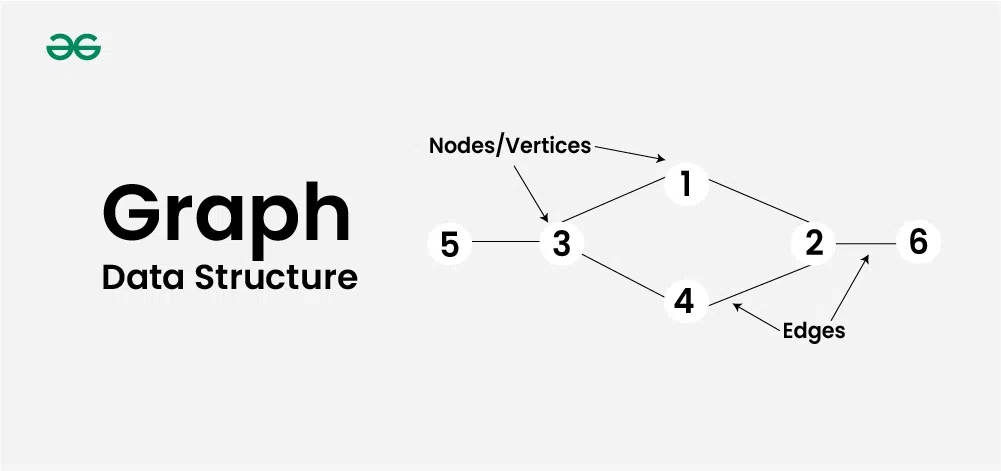
그래프는 노드vertex와 간선edge을 이용한 비선형 데이터 구조이다. 보통 그래프는 데이터 간 관계를 표현하는 데 사용한다.

• 노드 - 데이터
• 간선 - 노드 간 관계나 흐름

여기서 간선은 방향이 있을 수도 있고 없을 수도 있다. 만약에 관계나 흐름에서 정도를 표현할 필요가 있다면 가중치라는 개념을 추가하여 표현한다.

🗒️ 그래프 용어 정리

예를 들어 도시 간 인구 이동을 그래프로 표현하면 다음과 같다.

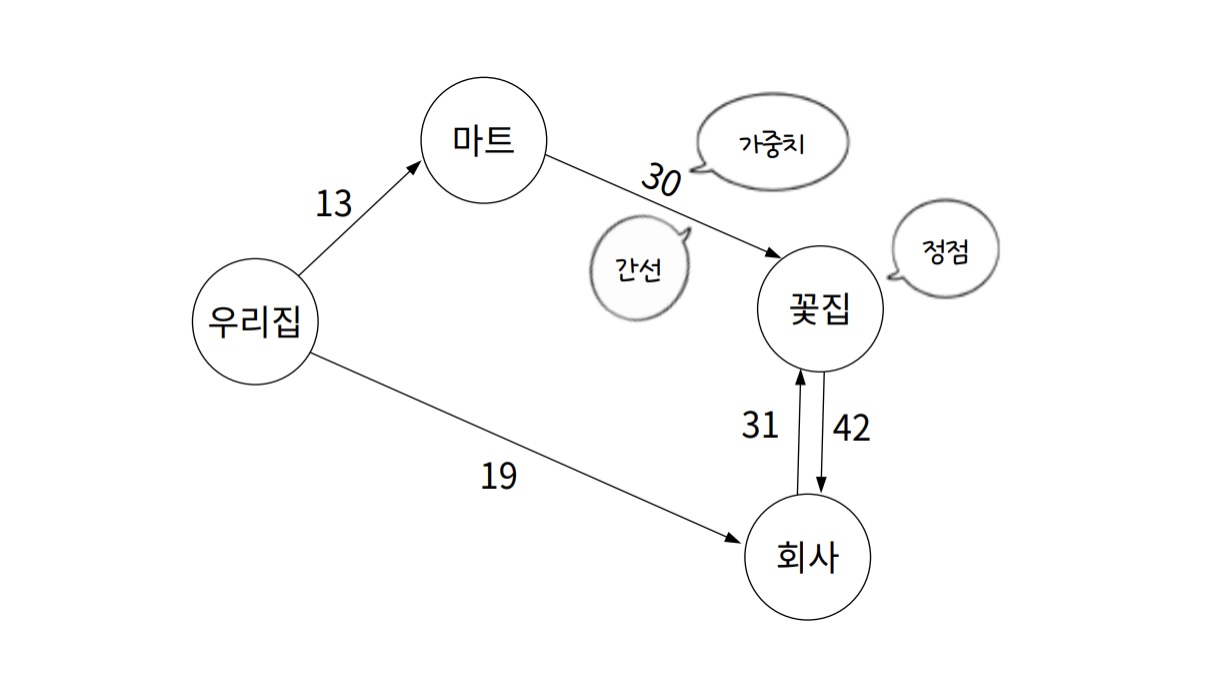
• 노드: 동그라미
• 간선: 화살표
• 가중치: 간선 위 숫자

노드에는 어떤 데이터가 들어있다. 그리고 노드 사이에 있는 것이 간선이다. 인구 이동의 경우 어디서 얼마나 이동했는지 표시해야 하므로 간선에 가중치를 표현했다.

---

🔍 그래프의 특징과 종류

1) 방향성에 따라 구분

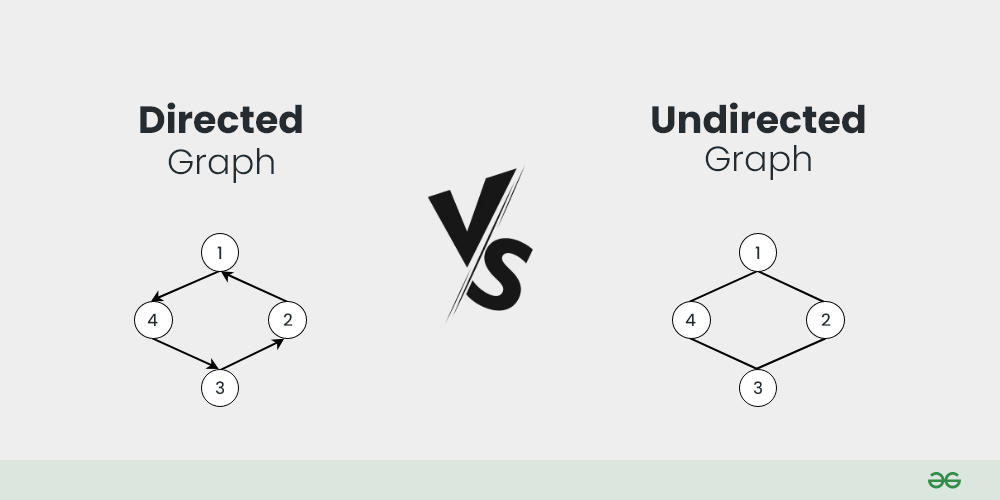
• 방향 그래프Directed Graph: 방향이 있는 간선을 포함한다. A에서 B로만 갈 수 있는 것과 B에서 A로만 갈 수 있는 것을 구분한다.

• 무방향 그래프Undirected Graph: 간선에 방향이 없어 A와 B가 서로를 연결하는 것으로 취급한다.

이때, 방향 그래프는 어느 한쪽으로만 간선이 있는 것이 아니라 정점이 서로를 가리키는 형태의 간선이 있을 수도 있다.

2) 가중치에 따라 구분

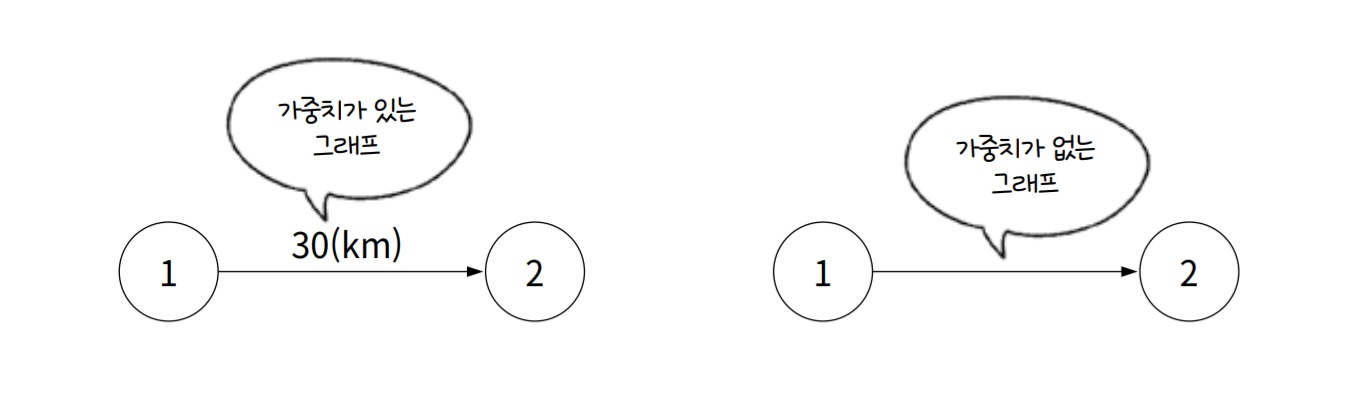
• 가중치 그래프Weighted Graph: 간선에 가중치가 할당된 그래프이다. 예를 들어, 도로망에서 각 도로가 가지는 거리나 비용을 나타내는 경우 등에 사용된다.

3) 순환에 따라 구분

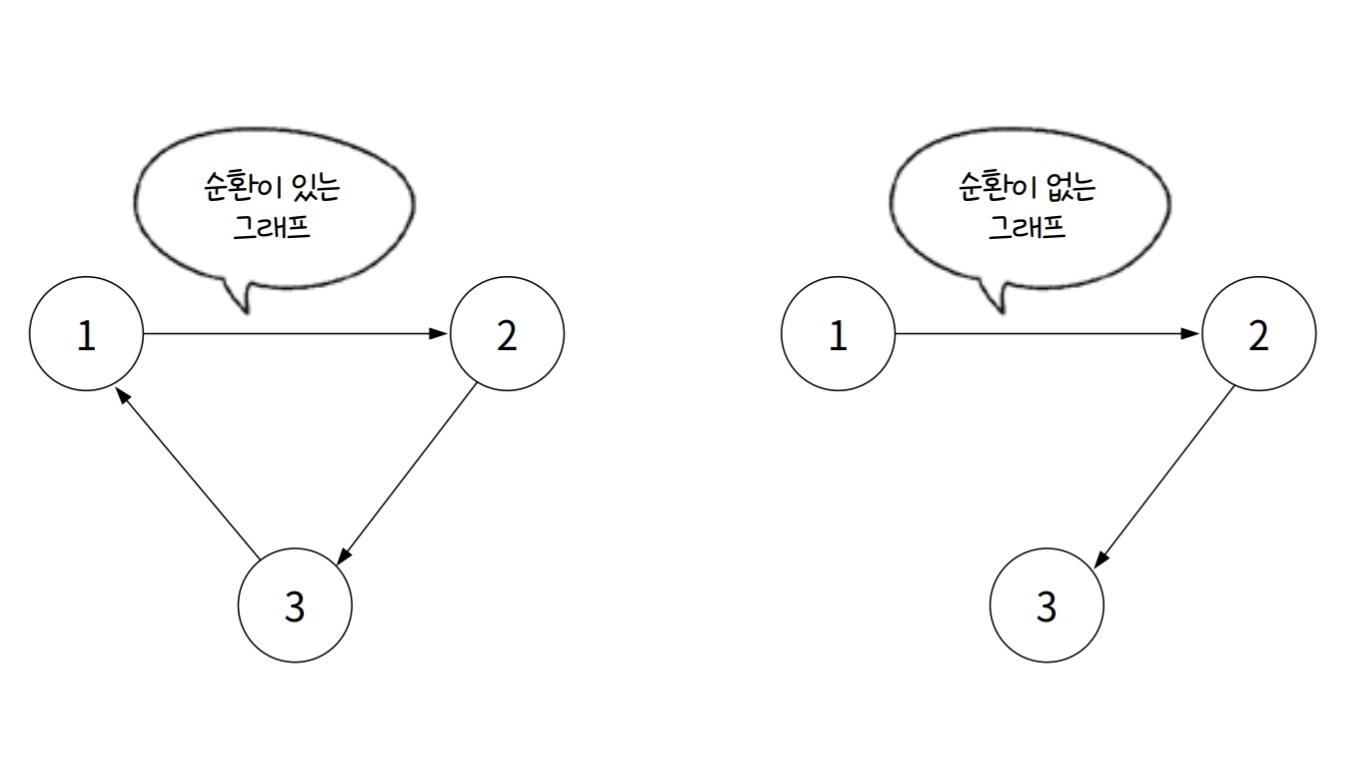
• 순환 그래프Cycle Graph: 특정 노드에서 시작해 간선을 따라 다시 돌아오는 경로가 있는 그래프

• 비순환 그래프Acyclic Graph: 순환이 존재하지 않는 그래프

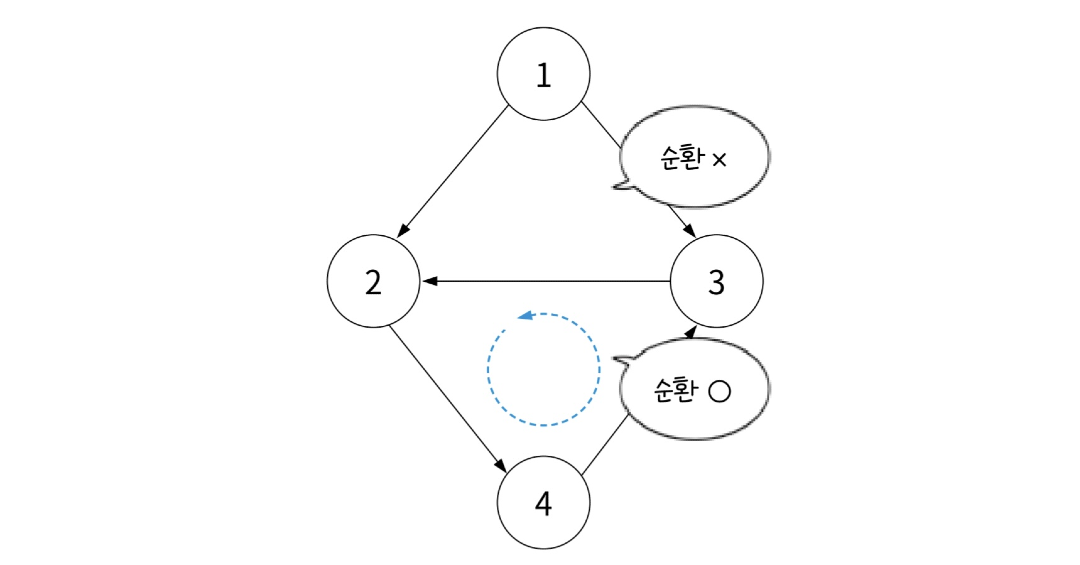
앞서 언급했듯 특정 노드에서 시작해 간선을 따라 다시 돌아오면 순환 그래프이다. 예시의 경우 2 -> 4 -> 3 -> 2이므로 그래프의 일부분이 순환된다. 1,2,3은 모두 연결되어 있긴 하지만 순환하진 않는다.

---

💻 그래프 구현

예를 들어 서울에서 부산으로 유동 인구가 8,000명 발생했다와 같은 내용을 그래프로 표현한다고 해보자. 그래프의 노드, 간선, 방향, 가중치와 문장의 의미를 이렇게 연결하여 정리할 수 있다.

• 데이터를 담고 있는 노드 (서울, 부산)
• 노드를 잇는 간선 (서울과 부산의 연결 유무)
• 간선의 방향 (서울 -> 부산)
• 간선의 가중치 (유동 인구 8,000명)

그래프의 구현 방시에는 인접 행렬adjacency matrix와 인접 리스트adjacency list가 있다. 두 방법으로 구현해보자.

1) 인접 행렬 그래프 표현

인접 행렬은 배열을 활용하여 구현하는 경우가 많다.

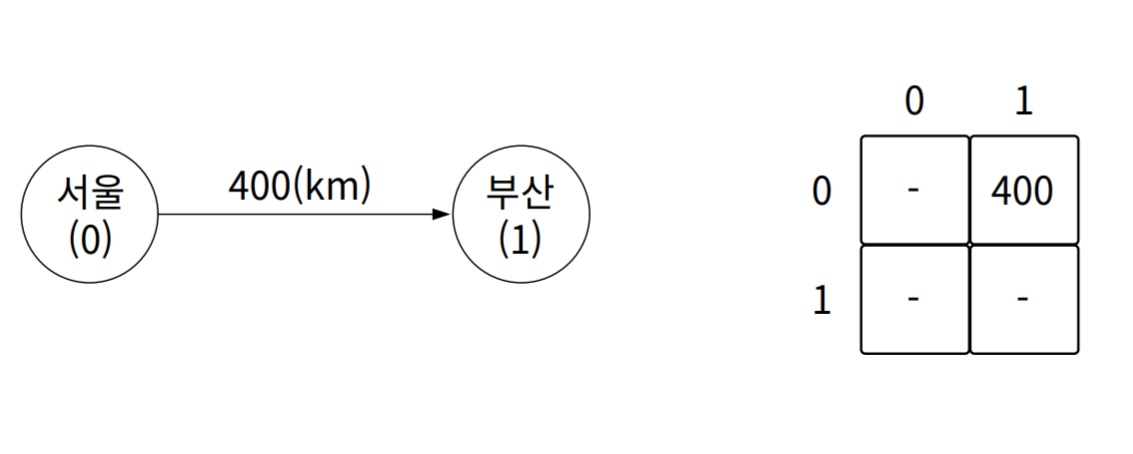
• 노드: 배열의 인덱스
• 가중치: 배열의 값
• 출발 노드: 인덱스의 세로 방향
• 도착 노드: 인덱스의 가로 방향

인접 행렬로 표현하면 세로 방향 인덱스를 출발, 가로 방향 인덱스를 도착으로 하니 서울(0) -> 부산(1)으로 향하는 가중치가 400km인 그래프가 표현되었다. 그리고 -로 표현한 가중치는 실제 코드에서는 굉장히 큰 값을 넣거나 -1로 정한다.

---

2) 인접 리스트 그래프 표현

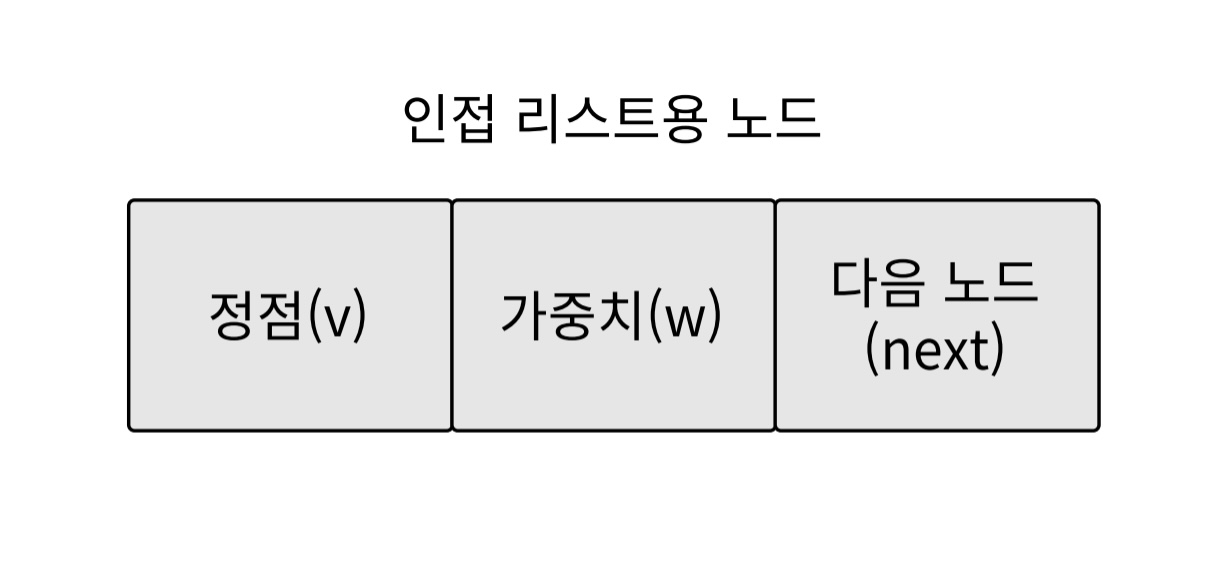
인접 리스트로 그래프를 표현하려면 우선 다음과 같이 적절한 노드를 정의해야 한다. 그림에서 보듯 값v, 가중치w, 다음 노드next를 묶어 관리한다.

인접 리스트 그래프 표현 방식

1. 노드 개수만큼 배열 준비: 각 정점마다 인접한 정점들을 연결 리스트LinkedList로 표현할 배열을 준비한다.

2. 배열의 인덱스는 각 시작 노드를 의미: 배열의 인덱스는 각 정점을 나타낸다. 예를 들어, 인덱스 0은 정점 A를 나타내고, 인덱스 1은 정점 B를 나타낸다.

3. 인접 리스트 구성: 각 정점마다 연결된 다른 정점들을 연결리스트로 관리한다. 연결 리스트의 각 노드는 연결된 정점의 정보를 가지고 있다.

예시 구현

1. 노드 개수만큼 배열 준비
   

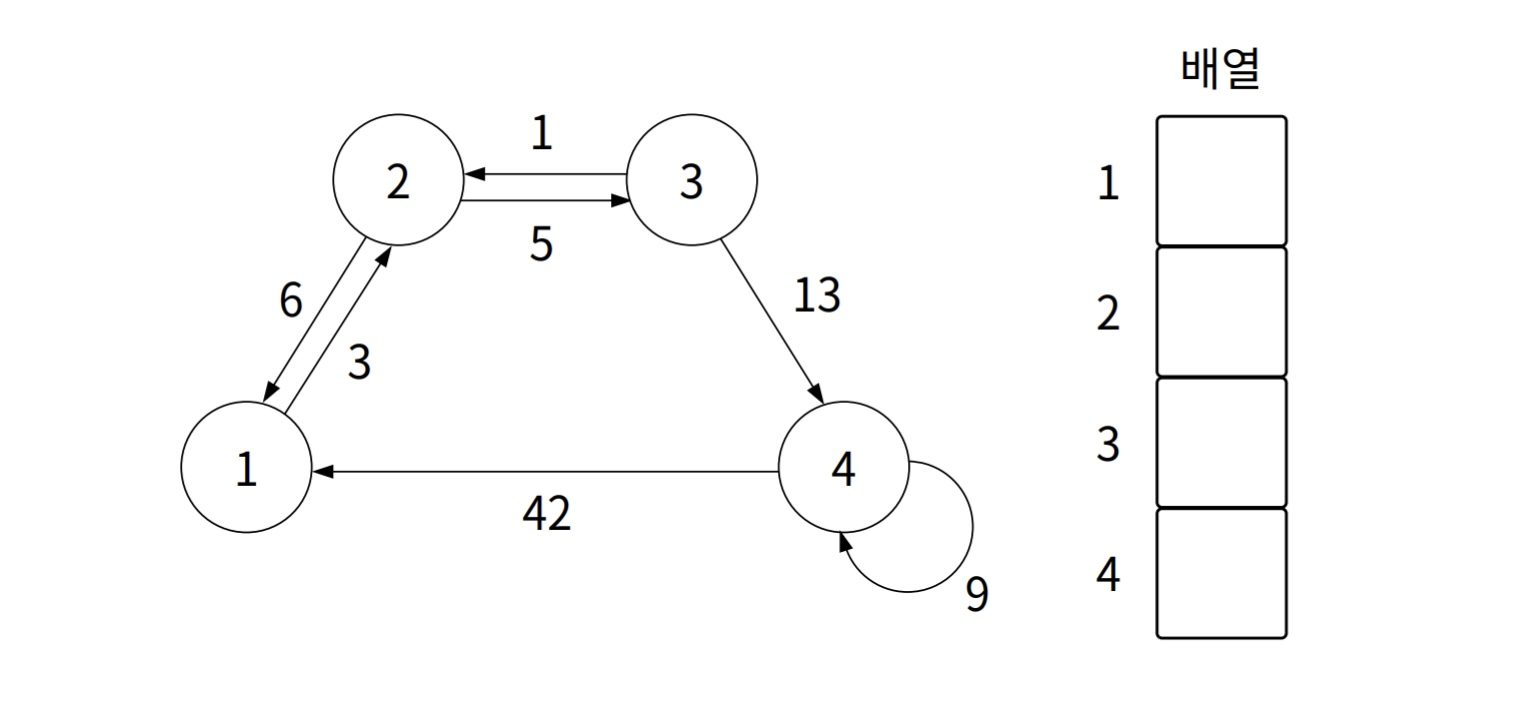
2. 1 -> 2(가중치 3) 표현
   

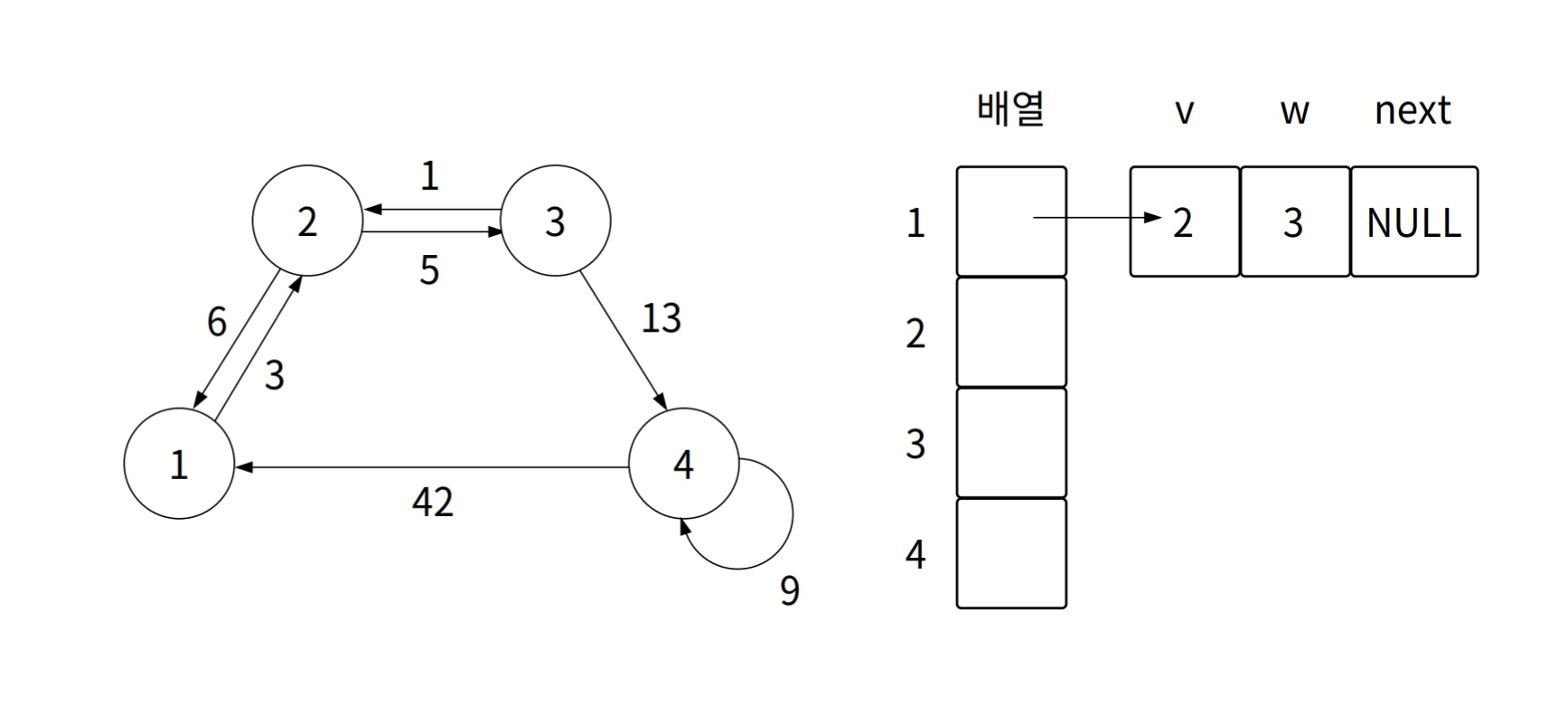
3. 2 -> 1(가중치 6) 표현
   

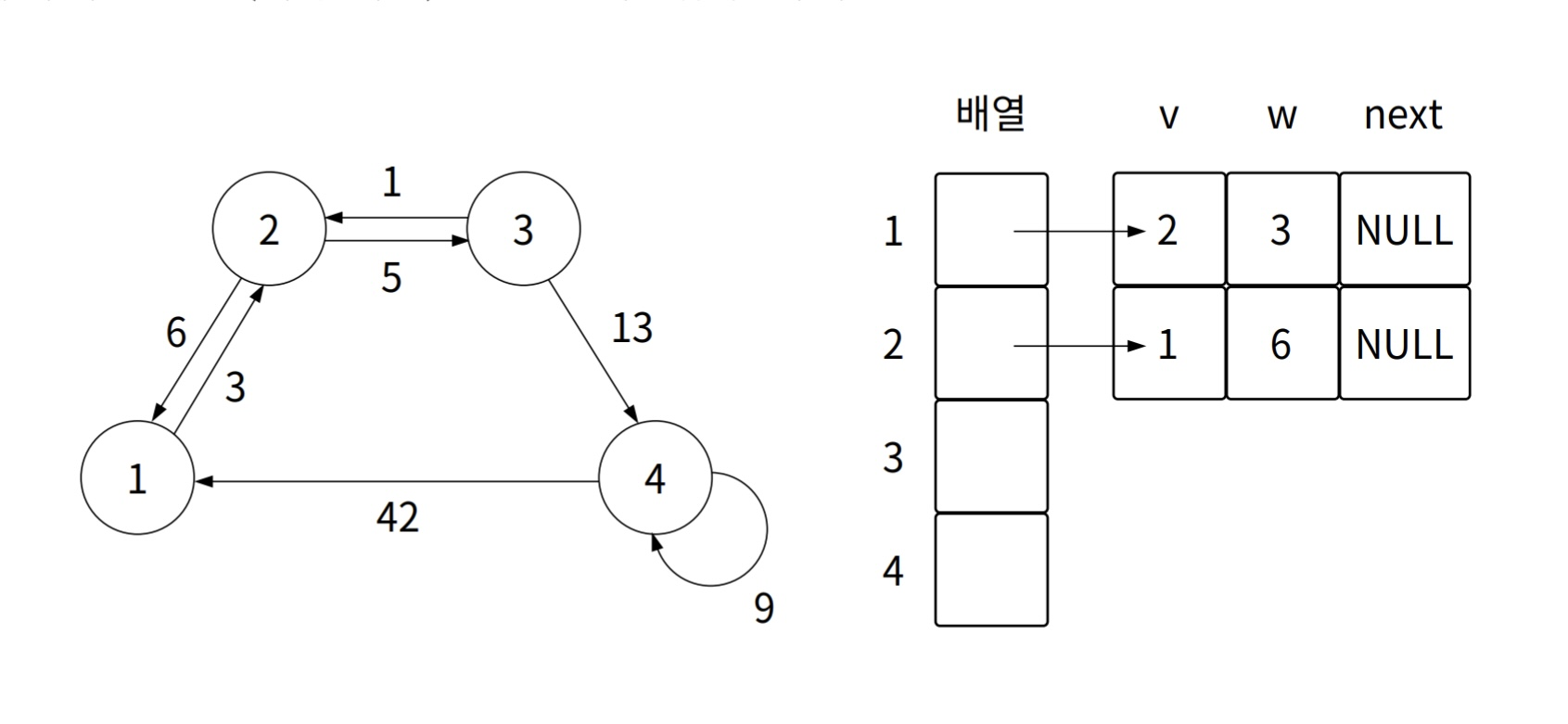
4. 2 -> 3(가중치 5) 표현
   

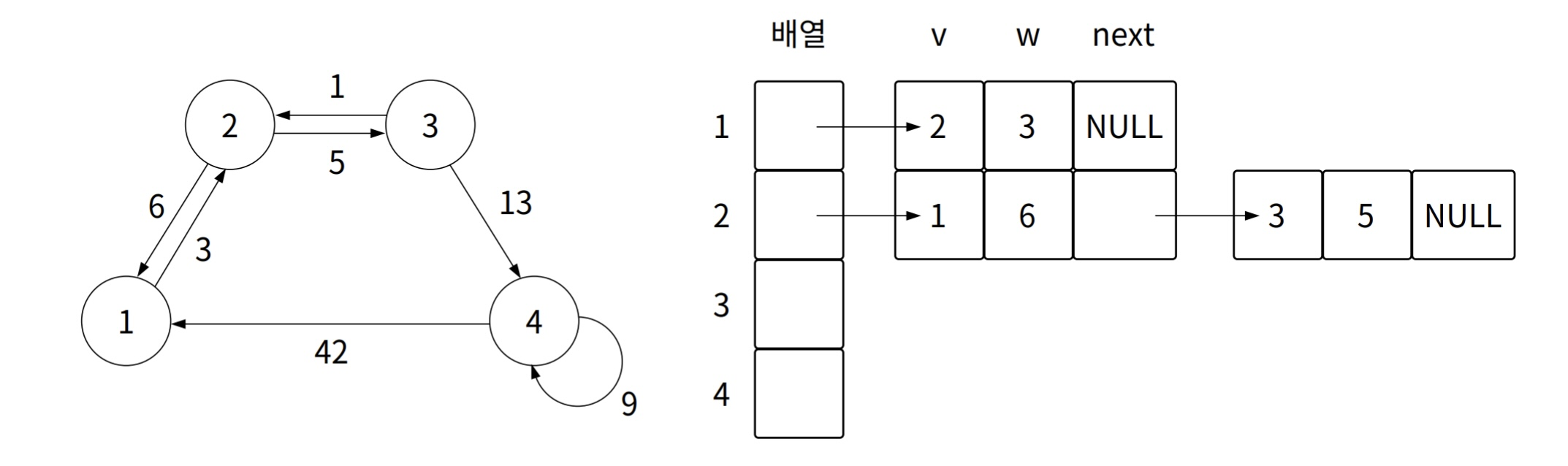
여기서 이미 배열에는 노드 2가 연결되어 있기 때문에, 다음 노드가 NULL인 노드를 찾아 2 -> 3(가중치 5)를 표현한 노드를 연결한다.

5. 인접 리스트 완성
   

---

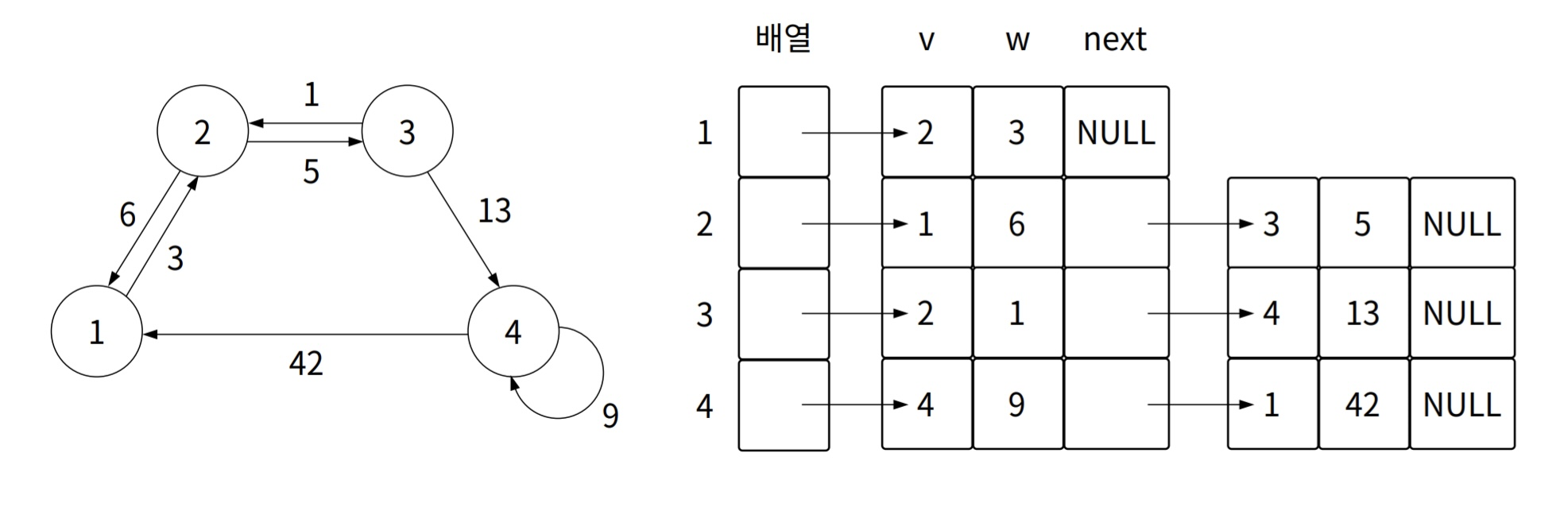
🆚 인접 행렬 vs 인접 리스트

인접 행렬

장점👍

• 간선 정보 탐색의 시간 복잡도: O(1)
  • 예를 들어 2에서 93이 연결되어 있는지 탐색하려면 array[2][93]에 가중치가 있는지만 확인하면 된다.
• 구현 난이도 ⬇️

단점👎

• 인접 행렬로 희소 그래프를 표현하는 경우
  • 인접 행렬은 크기가 고정되어 있으므로(노드가 N개 있을 때 N X N) 비효율적
• 노드들의 값의 차이가 매우 큰 그래프를 표현하는 경우
  • 노드값이 순차적으로 증가하지 않고 1,2,3,999와 같이 간격이 크면 가장 큰 노드의 값인 999를 기준으로 인접 행렬의 크기를 잡아야 함

💡 희소 그래프란?
노드 수에 비해 간선 수가 매우 적은 그래프를 말한다.

인접 리스트

장점👍

• 메모리를 아낄 수 있음
  • 인접 리스트는 실제 연결된 노드에 대해서만 노드의 값을 노드에 담아 연결하면 된다.

단점👎

• 탐색 시간이 O(N)
  • 특정 노드에서 시작하여 연결된 노드 개수가 많을수록 탐색 시간이 길어진다.
  • 최악의 경우, 탐색 시간 O(N)이 된다.

최종 정리

표로 정리한 인접 행렬과 인접 리스트의 장단점은 다음과 같다.

특성	메모리 사용	탐색 시간	구현 난이도
인접 행렬	O(N²)	O(1)	낮음
인접 리스트	O(N³)	O(N)	높음

그래프 문제를 풀 때는 더 좋은 것을 선택해야 하지만 보통은 시간 제약에서 장점을 취하기 위해 인정 행렬 방식으로 그래프 문제를 푸는 경우가 많다. **문제에서 노드 개수가 1,000개 미만으로 주어지는 경우에는 인접 행렬을 사용하면 된다.

💡 노드의 데이터가 숫자가 아닌 문자열이면, 문자열을 숫자로 매핑하여 인접 행렬의 인덱스로 사용하면 된다.