해시(Hash)란?
해시는 해시 함수를 사용해 변환한 값을 인덱스로 삼아 키와 값을 저장해서 빠른 데이터 탐색을 제공하는 자료구조이다. 보통은 인덱스를 활용해서 탐색을 빠르게 만들지만 해시는 키(key)를 활용해 데이터 탐색을 빠르게 한다.
해시는 키와 데이터를 일대일 대응하여 저장하므로 키를 통해 데이터에 바로 접근할 수 있다. 또한 키에는
String등의 자료형도 올 수 있으므로 사람에게는 배열보다 접근성이 좋은 자료구조라고 할 수 있다.
해시 자세히 알아보기
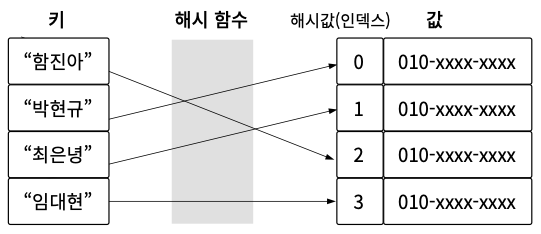
우리 생활에서 가장 쉽게 볼 수 있는 해시의 예는 연락처이다. 내가 최종적으로 얻고자 하는 정보, 즉 값value는 전화번호이고, 값을 검색하기 위해 활용하는 정보인 이름은 키key인 것이다.
그리고 그 사이에 키를 이용해 해시값 또는 인덱스로 변환하는 해시 함수가 있다. 해시 함수는 키를 일정한 해시값으로 변환시켜 값을 찾을 수 있게 해준다. (자세한 내용은 추후 다루도록 하겠다.)
해시의 특징
첫 번째, 해시는 단방향으로 동작한다. 즉, 키를 통해 값을 찾을 수 있지만 값을 통해 키를 찾을 수는 없다.
두 번째, 찾고자 하는 값을 O(1)에서 바로 찾을 수 있다. 키 자체가 해시 함수에 의해 값이 있는 인덱스가 되므로 값을 찾기 위한 탐색 과정이 필요 없다.
세 번째, 값을 인덱스로 활용하려면 적절한 변환 과정을 거쳐야 한다.
단방향으로만 동작하는 해시의 특성은 외부에 정보를 안전하게 제공한다는 특징이 있어 네트워크 보안에서 많이 활용된다.
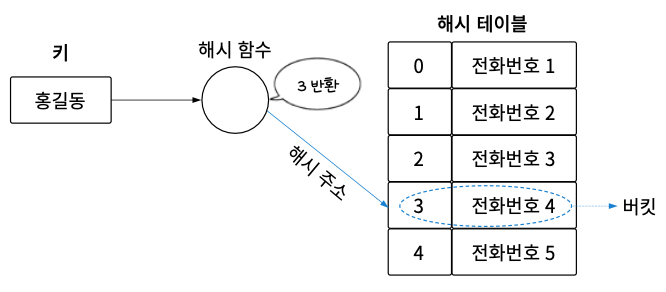
해시를 사용하면 순차 탐색할 필요 없이 해시 함수를 활용해서 특정 값이 있는 위치를 바로 찾을 수 있어 탐색 효율이 좋다. 그림에서 해시 테이블hash table은 키와 대응한 값이 저장되어 있는 공간이고, 해시 테이블의 각 데이터를 버킷bucket이라고 부른다.
해시의 특성을 활용하는 분야
해시는 단방향으로만 검색할 수 있는 대신 빠르게 원하는 값을 검색할 수 있다. 이런 해시의 특성은 데이터를 저장하고 검색하거나, 보안이 필요한 때에 활용된다. 코딩 테스트에서는 특정 데이터를 탐색하는 횟수가 많을 경우 해시를 고려하면 좋다. 다음은 해시가 활용되는 실제 사례이다.
비밀번호 관리
사용자의 비밀번호를 그대로 노출해 저장하는 것은 위험하므로 해시 함수를 활용해 해싱한 비밀번호를 저장한다. 비밀번호가 맞는지 확인할 때도 마찬가지이다. 사용자가 입력한 비밀번호를 해싱해 확인한다.
데이터베이스 인덱싱
데이터베이스에 저장된 데이터를 효율적으로 검색할 때 해시를 활용한다.
블록체인
블록체인에서 해시 함수는 핵심 역할을 한다. 각 블록은 이전 블록의 해시값을 포함하고 있으며, 이를 통해 데이터 무결성을 확인할 수 있다.
해시 함수
앞서 언급했던 해시 함수는 어떻게 구현할까? 사실 코딩 테스트에서 해시 함수를 직접 구현하라는 문제가 나오는 경우는 거의 없다. 그리고 파이썬에서는 딕셔너리Dictionary라는 자료형을 제공하는데, 이 자료형은 해시와 매우 유사하므로 해시를 쉽게 사용할 수 있다.
하지만 해시의 원리를 이해하고 딕셔너리를 사용하면 좀 더 효율적으로 딕셔너리를 사용할 수 있으므로 한 번쯤은 해시 개념을 공부하기를 추천합니다.
해시 함수를 구현할 때 고려할 내용
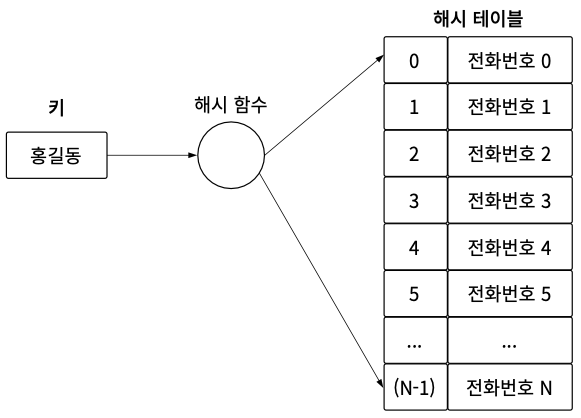
첫 번째, 해시 함수가 변환한 값은 인덱스로 활용해야 하므로 해시 테이블의 크기를 넘으면 안 된다. 다음 그림으로 예를 들어보겠다. 현재 해시 함수의 결과는 해시 테이블의 크기인 0과 N – 1 사이의 값을 내야 한다.
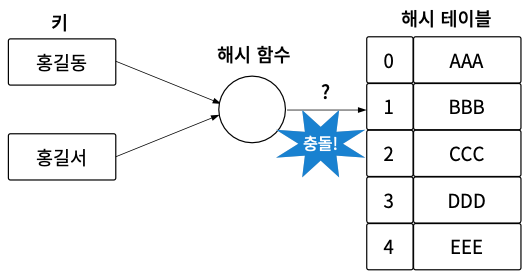
두 번째, 해시 함수가 변환한 값의 충돌은 최대한 적게 발생해야 한다. 충돌의 의미는 서로 다른 서로 다른 두 키에 대해 해싱 함수를 적용한 결과가 동일한 것을 의미한다. 다음과 같이 홍길동과 홍길서를 해시 함수에 넣었을 때 둘 다 결괏값이 1이면 저장 위치가 같다. 즉, 충돌이 발생합니다.
여기서 충돌이 최대한 적어야 한다라고 이야기한 이유는 충돌이 아예 발생하지 않는 해시 함수는 거의 없기 때문이다.

자주 사용하는 해시 함수 알아보기
그러면 이제 실제로 자주 사용하는 해시 함수를 알아보도록 하겠다.
나눗셈법
나눗셈법은 가장 떠올리기 쉬운 단순한 해시 함수이다. 나눗셈법Division Method은 키를 소수로 나눈 나머지를 활용한다. 이처럼 나머지를 취하는 연산을 모듈러 연산이라고 하며 연산자는 %로 표시한다. 예를 들어 7%2 = 1이다. 앞으로 나머지를 취하는 연산은 모듈러 연산이라고 하겠다. 나눗셈법을 수식으로 작성하면 다음과 같다.
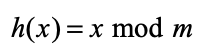
x는 키, k는 소수입니다. 키를 소수로 나눈 나머지를 인덱스로 사용하는 것이다. 나눗셈법을 그림으로 나타내면 다음과 같다.
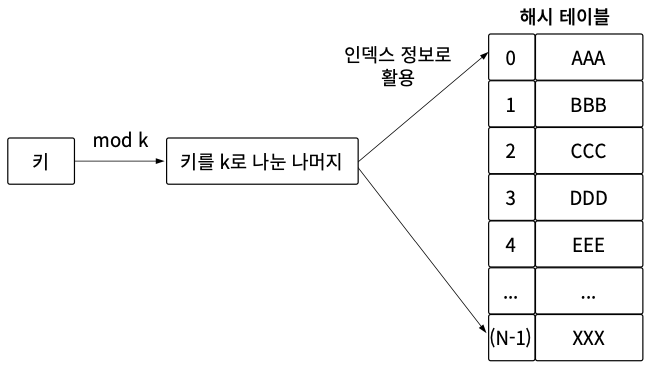
나눗셈법에 소수가 아닌 15를 사용하면 어떻게 될까?
소수를 사용하는 이유는 다른 수를 사용할 때보다 충돌이 적기 때문이다. 예를 들어 소수가 아닌 15를 나눗셈법에 적용했다고 해보자. 이때 x가 3의 배수인 경우를 한번 보면 규칙적으로 계속 같은 해시값이 반복되는 것을 알 수 있다.

나눗셈법을 적용하면 해시값은 3, 6, 9, 12, 0이 반복된다. 해시값을 보면 동일한 값들이 계속 반복되며, 이를 해시값이 충돌되었다고 표현한다. x를 5의 배수로 생각해도 충돌이 많이 발생한다.
따라서 K는 1과 자신 빼고는 약수가 없는 수, 즉, 소수를 사용하는 것이 좋다.
나눗셈법의 해시 테이블 크기는 K
그리고 나눗셈법은 해시 테이블의 크기가 자연스럽게 K가 된다. 왜냐하면 K에 대해 모듈러 연산을 했을 때 나올 수 있는 값은 0 ~ (K – 1)이기 때문이다. 즉, 상황에 따라 아주 많은 데이터를 저장해야 한다면 굉장히 큰 소수가 필요할 수도 있다. 아쉽게도 매우 큰 소수를 구하는 효율적인 방법은 아직은 없으며 필요한 경우 기계적인 방법으로 구해야 한다. 나눗셈법의 단점 중 하나이다.
곱셈법
이번에는 곱셈법Multiplication Method을 알아보도록 하겠다. 곱셈법은 나눗셈법과 비슷하게 모듈러 연산을 활용하지만 소수는 활용하지 않는다. 곱셈법의 공식은 다음과 같다.
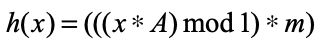
m은 최대 버킷의 개수, A는 황금비Golden Ratio Number입니다. 황금비는 무한소수로 대략 1.6180339887…이며 이 책에서 계산에는 황금비의 소수부의 일부인 0.6183만 사용했습니다.
황금비는 수학적으로 임의의 길이를 두 부분으로 나누었을 때, 전체와 긴 부분의 비율이 긴 부분과 짧은 부분의 비율과 같은 비율을 뜻한다.
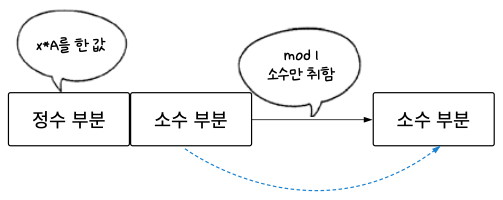
01단계 키에 황금비를 곱한다.
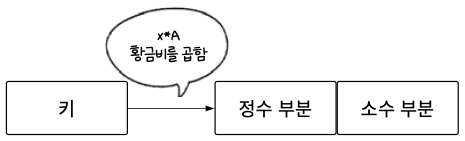
02단계 01단계에서 구한 값의 모듈러 1을 취한다. 쉽게 말해 정수 부분을 버리고 소수 부분만 취합니다. 예를 들어 모듈러 1의 결과가 3.1523이면 0.1523만 취한다. 소수 부분만 취하기 때문에 0.xxx 형태의 값이 나오게 된다.
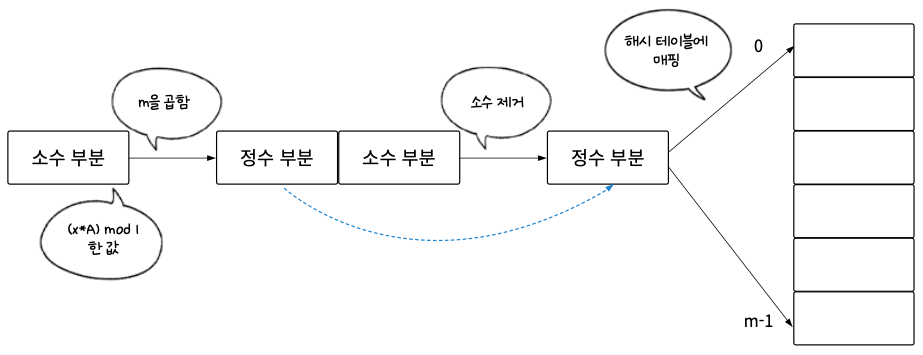
03단계 02단계에서 구한 값을 가지고 실제 해시 테이블에 매핑한다. 테이블의 크기가 m이면 02단계에서 구한 수에 m을 곱한 후 정수 부분을 취하는 연산을 통해 해시 테이블에 매핑할 수 있다. 02단계에서 구했던 값은 0.xxx의 값이므로 매핑할 테이블의 크기인 m을 곱하면 테이블의 인덱스인 0 ~ (m – 1)에 매치할 수 있다.
이처럼 곱셈법은 황금비를 사용하므로 나눗셈법처럼 소수가 필요 없다는 장점이 있다. 따라서 해시 테이블의 크기가 커져도 추가 작업이 필요 없다.
문자열 해싱
지금까지 알아본 해시 함수는 키의 자료형이 숫자였지만, 이번에는 키의 자료형이 문자열일 때도 사용할 수 있는 해시 함수인 문자열 해싱을 알아보겠다. 문자열 해싱은 문자열의 문자를 숫자로 변환하고 이 숫자들을 다항식의 값으로 변환해서 해싱한다. 공식은 다음과 같다.
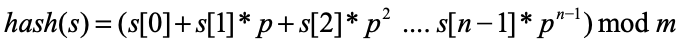
p는 31이고, m은 해시 테이블 최대 크기입니다. 이 수식이 실제 적용되는 과정을 그림과 함께 알아보자.
※ p를 31로 정한 이유는 홀수이면서 메르센 소수이기 때문이다.
- 메르센 소수는 일반적으로
2N-1형식으로 표시할 수 있는 숫자 중 소수인 수를 말한다. 메르센 소수는 해시에서 충돌을 줄이는데 효과적이라는 연구 결과가 있다.
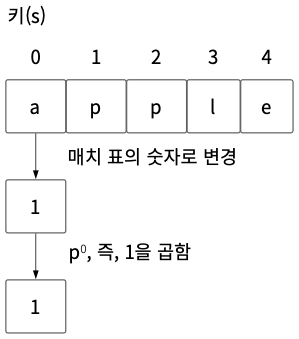
01단계 다음 그림은 알파벳 a부터 z까지 숫자와 매치한 표와 키이다.

02단계 “a”는 매치 표를 보면 1이다. 따라서 “apple”의 “a”는 1이다. 그러므로 수식의 s[0] * p0는 1 * 1이므로(31의 0승은 1) 1이다.
03단계 두 번째 문자열 “p”에 대해 연산을 진행한다. “p”는 16이다. 여기에 p1을 곱하면 496이다.
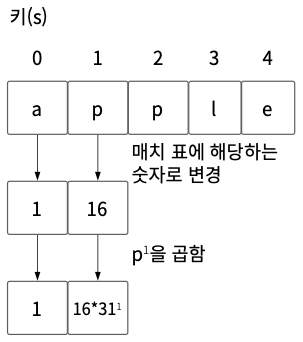
04단계 이렇게 곱한 값들을 더하면 최종값은 4,990,970이다. 이를 해시 테이블의 크기 m으로 모듈러 연산해 활용하면 된다.
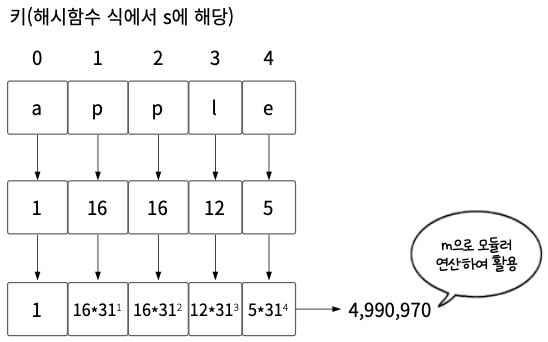
문자열을 키로 사용하여 해시 테이블을 구현할 때, 문자열을 숫자로 변환한 후 해시 함수를 적용해야 한다. 이 과정에서 주의해야 할 점은 해시 함수의 결과 값이 너무 커질 수 있다는 것이다. 이를 방지하기 위해 모듈러 연산을 활용한다.
모듈러 연산을 통해 큰 숫자를 해시 테이블 크기에 맞도록 조정할 수 있다. 예를 들어, "apple"이라는 문자열을 해싱했을 때, 결과 값이 4,990,970과 같이 매우 큰 값이 나올 수 있다. 이런 큰 값을 다룰 때 오버플로overflow 문제가 발생할 수 있으므로, 중간 중간 모듈러 연산을 사용하여 이 문제를 방지한다.
문자열 해시 함수 수정하기
해시 함수를 작성할 때, 큰 수의 오버플로를 방지하기 위해 덧셈 연산을 수행하는 중간 중간에 모듈러 연산을 적용하는 방식으로 수정할 수 있습니다.
기존 방식
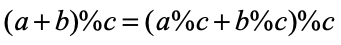
수정된 방식
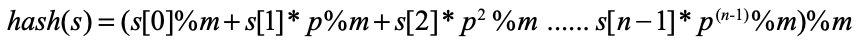
해시 함수뿐 아니라 보통 수식에 모듈러 연산이 있는 문제 중 큰 수를 다루는 문제는 이런 오버플로 함정이 있는 경우가 많다. 난이도가 높은 문제는 대부분 이런 함정을 포함하고 있으니 이번 기회에 제대로 기억해두자.
