충돌 처리
앞서 자주 언급했던 것처럼 서로 다른 키에 대해서 해시 함수의 결괏값이 같으면 충돌Collision이라고 한다. 하나의 버킷에 2개의 값을 넣을 수는 없으므로 해시 테이블을 관리할 때는 반드시 충돌 처리를 해야 한다.
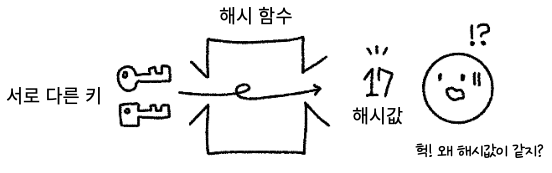
그림을 보면 두 키는 서로 다르지만 해시 함수를 적용해 해시값이 17이 나왔다. 이렇게 되면 해시 테이블의 같은 위치를 나타내므로 충돌이 발생한다. 여기서는 이런 충돌이 발생하면 어떻게 처리해야 하는지 알아보자.
체이닝으로 처리하기
체이닝은 해시 테이블에 데이터를 저장할 때 해싱한 값이 같은 경우 충돌을 해결하는 간단한 방법이다. 체이닝은 충돌이 발생하면 해당 버킷에 연결 리스트Linked List로 같은 해시값을 가지는 데이터를 연결한다.
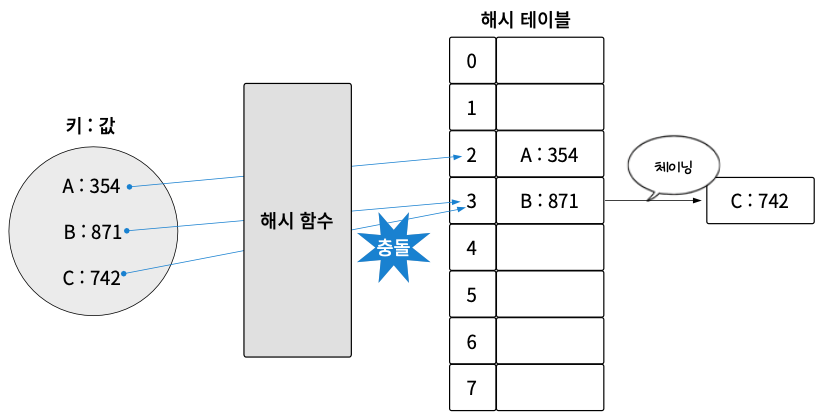
그림을 보면 키 B와 C를 해싱했을 때 3입니다. 즉, 해시 테이블의 같은 위치를 가리키므로 데이터를 저장할 때 충돌이 발생한다. 이때 체이닝은 링크드리스트로 충돌한 데이터를 연결하는 방식으로 충돌을 해결한다. 이후 어떤 데이터가 해시 테이블 상 같은 위치에 저장되어야 하면 이런 방식으로 데이터를 저장한다. 이처럼 체이닝은 충돌을 링크드리스트로 간단히 해결한다는 장점이 있지만 2가지 단점이 있다.
해시 테이블 공간 활용성이 떨어짐
충돌이 많아지면 그만큼 연결 리스트의 길이가 길어지고, 다른 해시 테이블의 공간은 덜 사용하므로 공간 활용성이 떨어진다.
검색 성능이 떨어짐
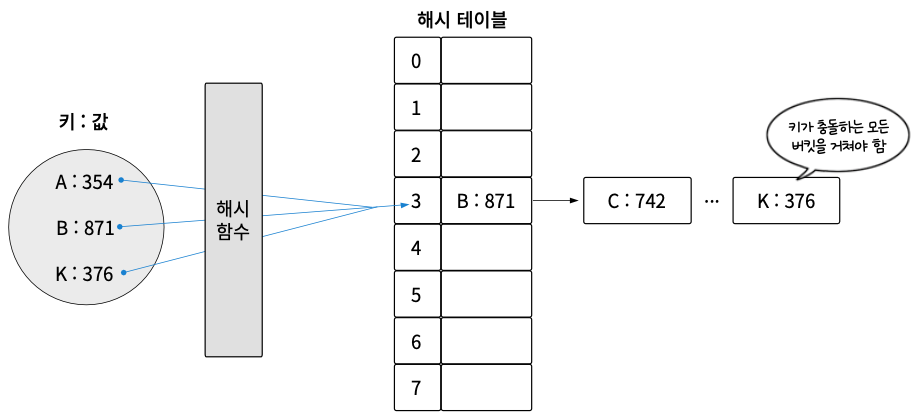
충돌이 많으면 연결 리스트 자체의 한계 때문에 검색 성능이 떨어집니다. 연결 리스트로 연결한 값을 찾으려면 연결 리스트의 맨 앞 데이터부터 검색해야 하기 때문이다. 만약 N개의 키가 있고 모든 키가 충돌하여 체이닝되었다면 마지막 버킷을 검색하는 경우 시간 복잡도는 O(N)이다.
개방 주소법으로 처리하기
개방 주소법Open Addressing은 체이닝에서 연결 리스트로 충돌값을 연결한 것과 다르게 빈 버킷을 찾아 충돌값을 삽입한다. 이 방법은 해시 테이블을 최대한 활용하므로 체이닝보다 메모리를 더 효율적으로 사용한다.
선형 탐사 방식
선형 탐사linear probing 방식은 충돌이 발생하면 다른 빈 버킷을 찾을 때까지 일정한 간격으로 이동한다. 수식은 다음과 같습니다.
※ 보통 간격은 1로 하는 것이 일반적이다.
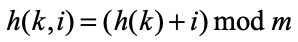
m은 수용할 수 있는 최대 버킷이다. 선형 탐사 시 테이블의 범위를 넘으면 안 되므로 모듈러 연산을 적용한 것이다. 수식을 그림으로 표현하면 다음과 같다.
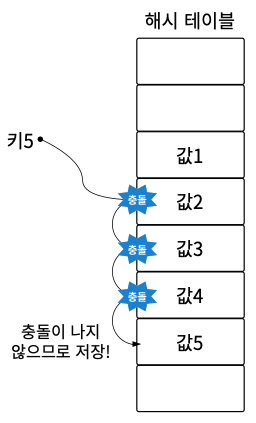
그림처럼 키 5에 해시 함수를 적용하여 값 2가 있는 위치에 충돌이 발생하면, 선형 탐사 방법으로 한 칸씩 이동하면서 값을 저장할 위치를 찾는다.
하지만 선형 탐사는 충돌이 발생한 값들이 연속적으로 모여 클러스터(Cluster)를 형성하게 된다. 이렇게 되면 충돌 발생 확률이 높아진다. 이를 방지하기 위해 제곱수만큼 이동하며 탐사하는 방법도 사용될 수 있다.
이중 해싱 방식
이중 해싱 방식은 말 그대로 해시 함수를 2개 사용한다. 때에 따라 해시 함수를 N개로 늘리기도 한다. 두 번째 해시 함수의 역할은 첫 번째 해시 함수로 충돌이 발생하면 해당 위치를 기준으로 어떻게 위치를 정할지 결정하는 역할을 한다. 예를 들어 보겠다. h1이 1차 해시 함수, h2가 2차 해시 함수이다.
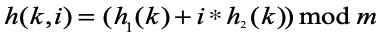
수식을 보면 선형 탐사와 비슷하게 더하는 방식으로 데이터의 위치를 정하지만 클러스터를 줄이기 위해 m을 제곱수로 하거나 소수로 한다. 이는 주어지는 키마다 점프하는 위치를 해시 함수로 다르게 해서 클러스터 형성을 최대한 피하기 위함이다.
결론
지금까지 해시에 대해 알아보았다. 해시 함수를 직접 구현하는 문제는 드물지만, 해시 개념은 IT 기업 입사 시 필수적인 기본 지식이므로 잘 이해하고 정리해두어야 한다.
- 핵심 개념: 키와 값을 매핑하는 과정
- 적용 상황: 빈번한 검색이 필요하거나 특정 정보와 매핑된 값을 확인해야 하는 경우
해시의 개념을 잘 이해하고 있으면, 면접에서 해시 관련 질문에 충분히 대답할 수 있을 것이다.
