배차 최적화 알고리즘을 개발하면서 강화학습을 공부했고, 강화학습을 배차에 적용한 논문이 있어 이를 분석하게 됐다. 해당 논문에선 실시간으로 승객과 택시를 매칭해주는 플랫폼의 배차 알고리즘에 대해 설명하고 있다.
On-Demand Ride-Hailing이란?
승객이 요청을 보내는 즉시 위치한 곳으로 모빌리티 서비스를 전달해주는 시스템 ex) 카카오택시, 디디추싱
Introduction
기존 택시 승객 매칭 방법
- 거리가 가장 가까운 승객 또는 선착순으로 선택하는 greedy methods 사용
- 구현 및 관리가 쉽지만 개발자가 모든 case들을 조정해줘야 하고, global 관점에서 효율보다 승객의 즉각적인 만족을 우선시 함
- 장기적 관점에선 optimal이 아닌 suboptimal
디디추싱 승객 매칭 방법
- 특정 지역에서 운전자가 얻을 수 있는 최대 이익을 계산해 승객 매칭
- 강화학습의 기반이 되는 MDP(Markov Decision Process) 이용
Online Planning Step & Offline Learning Step
- Offline Learning Step에선 과거 데이터의 승객 수요 및 택시 공급 패턴을 기반으로 시공간 상태에 대한 evaluation metric을 구축
- Online Planning Step에선 구축한 evaluation metric(value functions)과 즉각적인 보상을 더해 Future reward를 계산해 운전자의 주문을 선택
Background and System Overview
기존 택시 서비스
- 승객의 요청을 받기 위해 거리를 돌아다님
- 운전자가 승객의 주문을 선택하는 방식 (driver-select-order)
Centralized decision (중앙 집중식 의사 결정)
- 플랫폼이 주문을 운전자에게 할당 (platform-assign-order-to-driver)
Decision Process
1) 택시는 지리적 좌표와 점유 상태를 지속적으로 업로드
2) 승객이 on-demand 요청을 생성하면 플랫폼에서 즉시 주문
3) 과거 데이터와 실시간 택시 모니터링 정보를 계산하여 최적의 매칭
Learning
Problem Statement
MDP definition
- 독립 드라이버를 agent로 모델링
- 개별 드라이버를 구별하지 않음 (모든 드라이버는 동일)
Action
Serving과 Idle로 구분
- Serving : agent(드라이버)는 지정된 장소로 이동해 승객 픽업 후 reward를 받음
- Idle : 특정 장소에서 유휴 상태이며, reward 없이 다음 state로 전이
State Transition & Reward Distribution
- t시점에서 승객이 지불해야 하는 금액과 운행이 완료되는 시간을 포함한 미래에 대한 정보가 없음
- 따라서 결정을 내릴 때 예상 도착 시간과 예상 가격에 의존
- 이러한 추정 오차 분포는 암시적으로 state transition probability P와 random distribution R에서 추정 가능
Pass' : a 액션 시 s → s'일 확률
Rass' : a 액션 시 s → s'의 rewardState
- 시간과 지역을 포함한 2차원 벡터로 구성
|S| = |T| × |G| (T는 time index, G는 region index의 집합)Reward
- 주문 가격, GMV(총 거래금액) 최대화가 goal
Discount Factor
- MDP가 미래를 내다보는 정도를 제어하는 요소
Example Problem
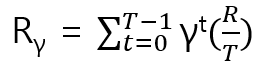
T = time slots, R = Price
문제
A지역 운전자가 00:00에 B에서 C로의 주문을 받았다.
이동은 20분 안에 완료될 것으로 예상되며 비용은 30$이다.
운전기사가 승객을 픽업하는데 10분이 소요된다.
time slot = 10, discount factor = 0.9Solve
s = (A, 0) , s’ = (B, 3) ( 3 = 2(이동 시간) + 1(픽업 시간) )
R = 30, T = 30 / 10 = 3, R/T = 10
∴ r = 10 + 10 0.9 + 10 0.9^2 = 27.1
Policy Evaluation
- MDP Definition에 기반해 과거 데이터를 (s, a, s’, r) 쌍의 transaction 으로 분류
- 개별 운전자를 구분하지 않기 때문에 모든 운전자에 대한 transaction은 value function 학습을 위한 dataset이 될 수 있음
- value function은 policy evaluation의 개념에 해당
Idle action일 때 Temporal-Difference update
V(s) ← V(s) + α[0 + γV(s') - V(s)]
current state s = (t, g)
future state s' = (t+1, g)
→ 시간이 흘러 t정보는 변했지만 유휴 상태이므로 지리 정보 g는 동일Serving action일 때 Temporal-Difference update
V(s) ← V(s) + α[Rγ + γΔtV(s'') - V(s)]
current state s = (t, g)
future state s'' = (t+Δt, gdestination)
t+Δt : 운전자가 주문 완료를 위한 예상 시간
gdestination : 승객이 플랫폼에 제공한 목적지Policy Evaluation
과거 정보 데이터셋 D={(si, ai, ri, s'i)}; si=(ti, gi에서 Dynamic Programming을 이용해 계속해서 V(si)을 update하며 최종 V(s) 값을 구함
Planning
학습된 value function을 input으로 사용하고 운전자와 주문 간 최종 일치를 실시간으로 결정
Dispatch algorithms' Objective function

subject to 부분을 확인하면,
- 운전자가 주문을 선택하거나 아무것도 하지 않는 action 중 하나를 선택하도록 보장
- 각 주문은 최대 한 명의 운전자에게 할당
- 운전자와 주문을 노드의 두 집합으로 하는 이분 그래프 형태이고, 두 노드 사이의 weight는 Qπ(i, j)
- i = j = 0인 경우는 타임스탬프에서 어떤 주문도 제공하지 않는 special default action에 해당
Advantage Function Trick
- default action : 운전자가 아무것도 하지 않고 주문이 제공되지 않음
- default action이 있는 경우 그래프는 운전자와 주문 사이에 가능한 모든 에지가 존재
- 계산 복잡성을 줄이기 위해 default action을 나타내는 모든 edge 제거
- 주문 발송과 다음 주문 발송 사이의 간격은 초 단위고, value function의 시간은 분 단위로 훨씬 작다. 따라서 타임스탬프에서 아무것도 하지 않는 운전자는 같은 state에서 아무것도 하지 않는 것으로 남아 있을 수 있음
- action-value function Q(i,0)은 운전자 i의 value function과 동일
- 운전자 i에 연결된 모든 edge에서 V(i)를 제외시켜 운전자와 ‘아무것도 하지 않음’ 액션 사이의 연결 제거 가능
Advantage Function
Aπ(i, j) = γΔtj( V(s'ij) - V(si) + Rγ(j) )
- 운전자 i와 주문 j 사이의 expected reward(s' state에서의 value function * 해당 시점의 discount factor)
→ expected value of remaining in the same state
(운전자의 현재 상태의 value function = 같은 state에서 order를 받지 않고 남아 있을 때의 expected value) + j order의 주문 가격Advantange Function을 최대화하는 운전자 i와 주문 j를 찾는 것이 objective function
Real-time order dispatch algorithm
1) V(s) 계산
2) 모든 가능한 운전자 i와 주문 j를 수집
3) Advantage Function Trick을 이용해 유효하지 않은 연결 제거
4) 운전자-주문 쌍에 대해 Advantage Function 계산
5) KM 알고리즘을 이용해 각 edge를 한 개씩만 유지
6) 관련 운전자와 승객에게 매칭 정보 전달
7) 매칭되지 않은 주문과 운전자는 다음 루프로 전달
영향 요소
Order Price
더 높은 효용 가치를 가진 주문 j는 자연스럽게 더 높은 이점으로 이어짐
운전자 위치
운전자의 현재 상태에 대한 value function은 advantage function에 부정적 영향
Order destination
가치 있는 지역의 주문은 더 높은 value function으로 이어짐으로 더 높은 이점
픽업 거리
픽업 거리가 길수록 승객을 픽업하는데 더 시간이 소요됨. 이로 인해 도착 시간이 늦어지고 목적지 value function에 더 큰 discount를 도입하므로 이점 감소
Combine Learning and Planning
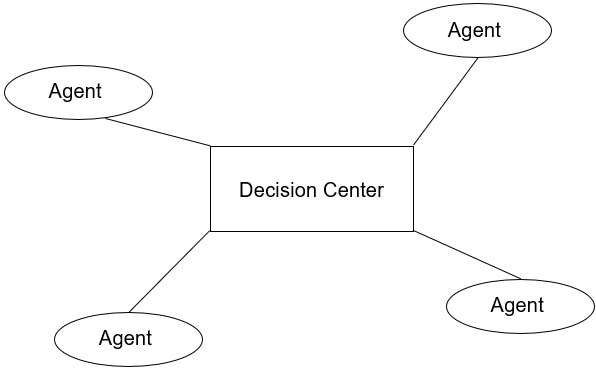
Decision Center가 모든 agent에게 결정을 내리는 meta-agent 역할
meta-agent가 연속적인 시간에서 결정을 내리고, 다음 몇 시간 동안의 총 기대 수익을 관찰
제안된 알고리즘의 주요 아이디어
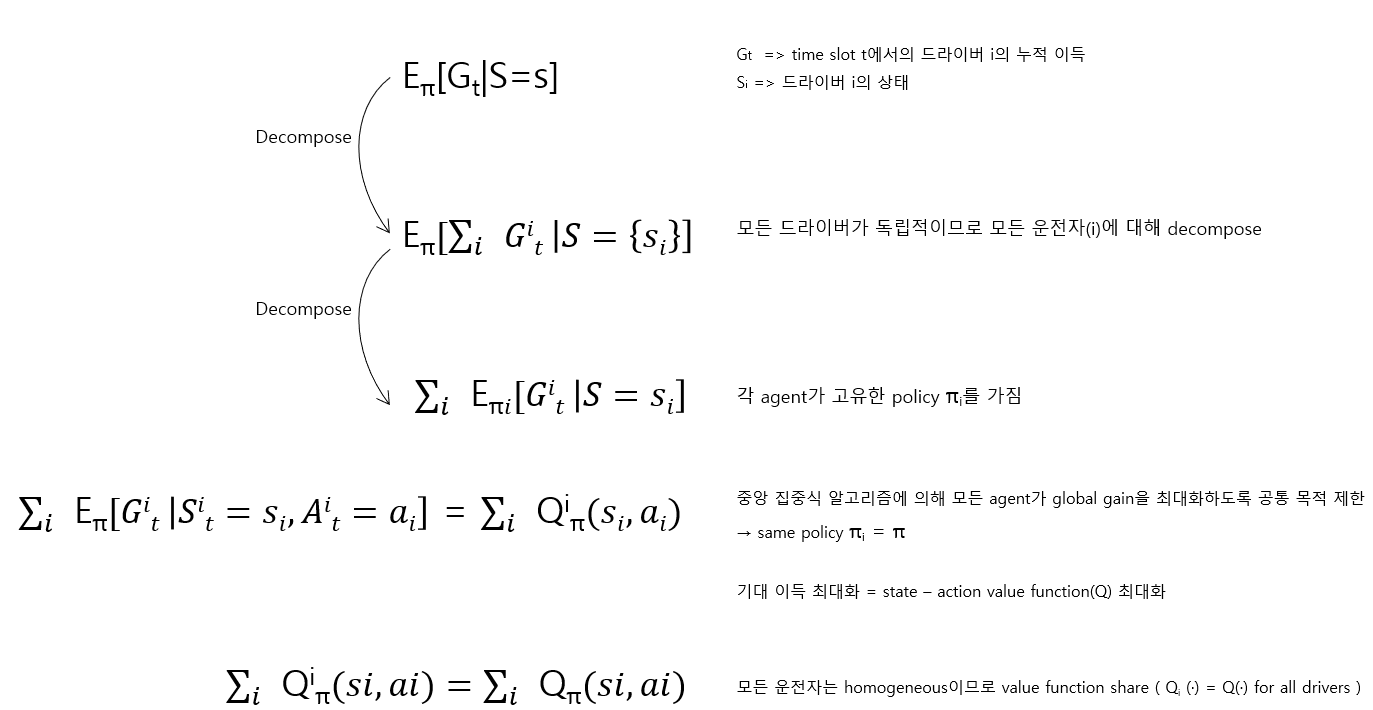
Experiment
Toy Example
문제 정의
- 9 X 9 grids with 20 time steps
- driver들은 각 time step에서 수직/수평으로 이동하거나 머무르도록 제한
- 주문은 맨해튼 거리가 2보다 크지 않은 운전자에게만 dispatch
- 주문이 어떤 운전자에게도 오랫동안 배차되지 않으면 취소됨
- 취소 시간은 range(0, 5), mean = 2.5, std = 2의 truncated Gaussian distribution
- 데이터 생성을 위해 주거 지역과 작업 지역의 다양한 위치에 집중된 morning-peak와 night-peak로 현실적인 교통 패턴을 시뮬레이션
- 주문 시작 위치는 two-component mixture Gaussians에 따라 샘플링되고 시공간 grid에서 정수로 잘림
- 주문의 목적지와 운전자의초기 위치는 discrete uniform 분포에 의해 무작위로 생성
Toy Example Result Comparison
- distance-based dispatch method, myopic greedy approach, MDP 세 가지 방법 비교
- 100개의 주문을 사용하며 driver 수는 각각 25, 50, 75로 수행
distance-based : driver와 order 사이의 거리만 고려
myopic greedy approach : 즉각적인 reward인 주문 가격만 고려
MDP : distance-based method에서 transaction을 수집하고 DP 알고리즘 수행Result
- 픽업 거리는 거리 기반 방법이 가장 최상의 성능
- MDP가 거리 기반 및 myopic보다 더 나은 수익 및 응답률을 달성
- MDP에서 driver-order 비율이 증가함에 따라 성능 향상이 약간 감소하는 현상
→ 공급보다 수요가 많을 때 최고의 성능 발휘
Experiment의 Simulator, Real-world Experiment, Related works, Conclusion 부분은 깊게 연구하지 못했지만, 결국 논문은 강화학습이 장기적 관점에서 다른 method들 보다 높은 이득을 기대할 수 있다는 것을 말하고 있다.