오늘은 sequential data를 처리하는 데 용이한 RNN에 대해 배워보도록 하겠습니다. 특별히 lec 9보다 이번 lec 10의 리뷰를 먼저 진행하게 되었는데, 그 이유는 딥 러닝 프로세스에서 아주 중요한 모델인 Transformer를 이해하기 위해선 RNN 및 seq2seq라는 모델에 대한 이해가 필요하기 때문입니다.

RNN's Process Sequence

우리가 기존까지 배운 Neural Network의 process sequence입니다. 하나의 입력을 넣으면 하나의 출력이 나오는 1대1 함수와 같은 개념이었죠?

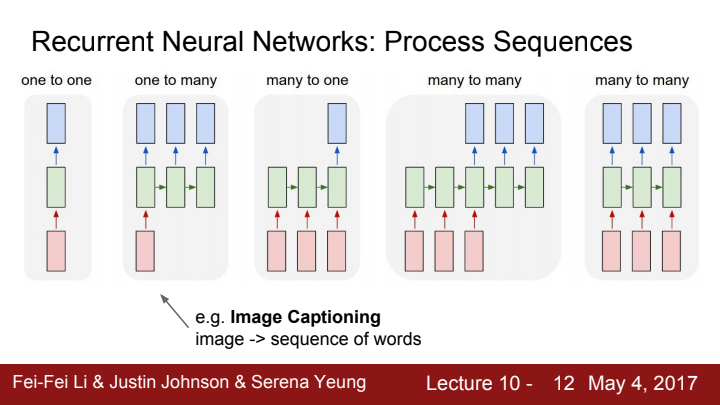
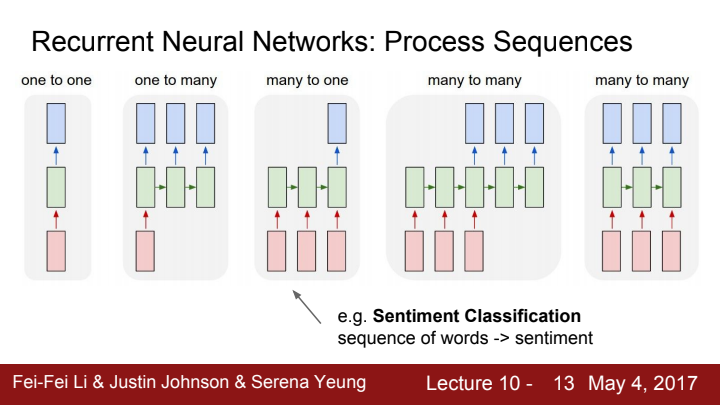
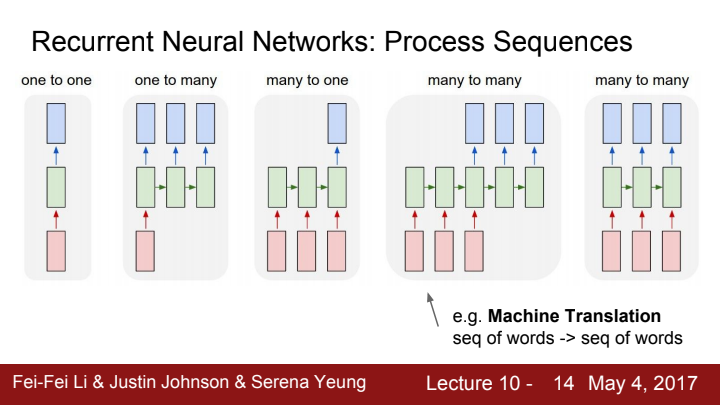
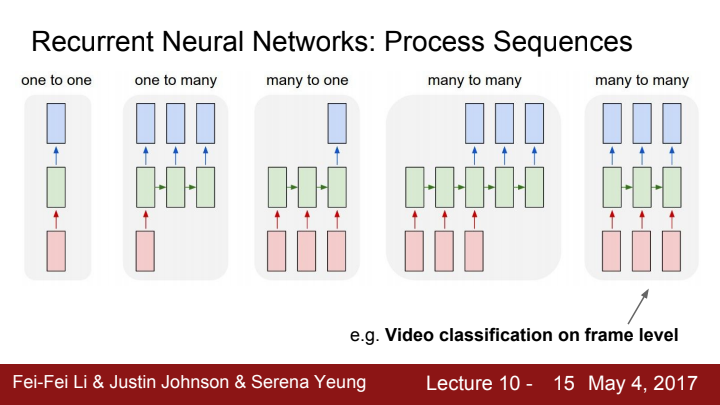
RNN은 기본적으로 sequential한, 즉 순차적인 성질을 지니고 있는 데이터를 처리하기에 용이합니다. 예를 들자면 "나는 밥을 먹었다"라는 문장에서, "나는", "밥을", "먹었다" 라는 세 가지 단어들은 그 순서를 지켜야만 올바른 문장이 됩니다. RNN은 이 단어들을 순서에 맞게 입력으로 받아들이거나 data를 처리하고 output을 내보내는 것이죠.

RNN의 process seqeunce는 input과 output의 개수가 한 개이냐 여러 개이냐에 따라 one-to-one, one-to-many, many-to-one, many-to-many로 분류가 됩니다.

Sequential Processing of Non-Sequence Data

cs231n은 Computer Vision 강의인데 RNN을 배운다는 것은, image같이 sequential하지 않은 데이터 또한 처리할 수 있다는 의미이겠죠?

Image Classification task에선, image를 여러 부분으로 쪼개준 뒤 그 쪼개진 부분들을 series로 "glimpse(힐긋 쳐다보기)"해줍니다! 말 그대로 이미지를 몇 조각으로 쪼개 순서대로 그 조각들을 스윽 쳐다본 뒤 image를 classify하는 것이죠.

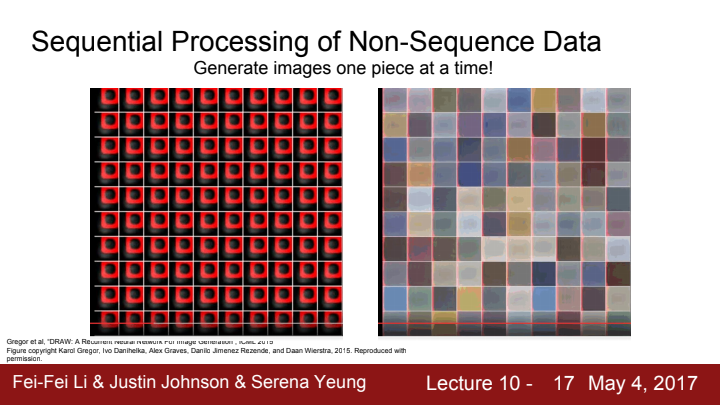
여기선 train 때 배운 data들을 기반으로 새로운 이미지를 생성하는 과정을 보여주고 있습니다. 이 곳에서도 RNN을 활용할 수가 있습니다. 앞서 했던 것처럼 순차적으로 이미지의 일부분씩 생성해가며 전체 image를 완성시키는 것입니다. 예를 들어 동그란 원을 하나 그린다고 하면, image를 4조각으로 나누어 순서대로 1, 2, 3, 4사분면을 그려줄 수 있겠죠?

Recurrent Neural Network

이제 본격적으로 Recurrent Neural Network, RNN의 구조에 대해 설명해보도록 하겠습니다.

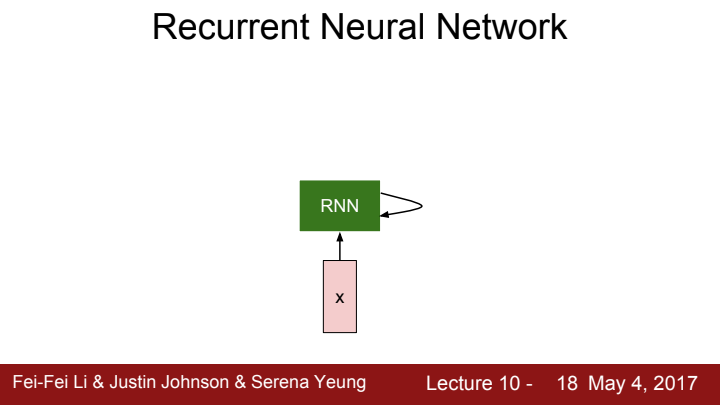
RNN은 기본적으로 core cell이라고 하는 구조를 포함하고 있습니다. input x가 RNN으로 입력될 때마다 core cell 내부의 internal hidden state가 update됩니다. update된 hidden state는 core cell로 feedback되며, 다음 time step에 새로운 input이 들어오게 됩니다.

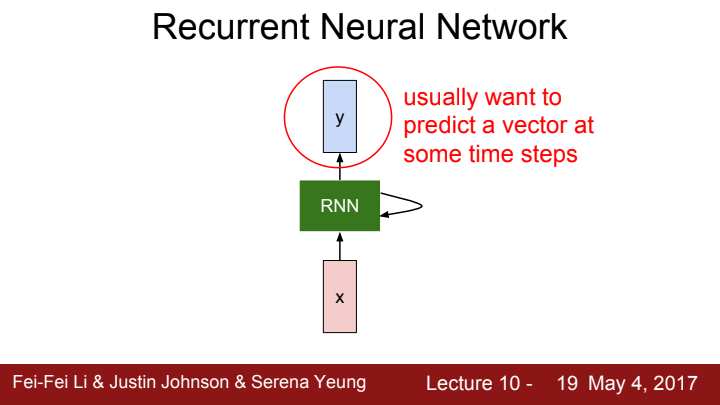
우리는 RNN으로 하여금 특정 time step에 input에 대한 output을 출력해주기를 원합니다. 이는 어떤 process인지에 따라 매 time step마다일수도 있고, 혹은 몇 step의 주기마다 일 수도 있고, 마지막 step에 한 번 일수도 있겠죠?

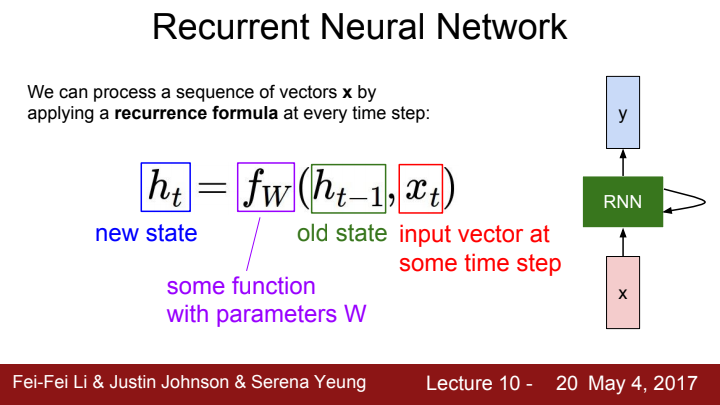
core cell 내부의 hidden state를 update를 수행해주는 함수 $f_W$가 필요합니다. 이 $f_W$에 이전 step에서의 hidden state와 현재 time step의 input을 input으로 넣어주게 되면 RNN의 state를 새롭게 update해줄 수 있는 것입니다. $f_W$는 그 이름에서 알 수 있듯이 parameter $W$를 가지고 있는 함수입니다.

참고로 Computation 과정에서 sequence 전체가 같은 weight을 사용하게 된다는 것을 알아주셨으면 합니다. 아직까진 감이 잘 안 오시죠?

Vanilla RNN의 기본 구조를 더 정확히 설명드리도록 하겠습니다. non linearity function인 tanh 함수에 입력으로 $W_{hh}h_{t-1}+W_{xh}x_t$를 입력해줍니다. 여기서 $W_{hh}$는 hidden-to-hidden weight으로, 이전 time step의 hidden state와 multiplication해줍니다. $W_{xh}$는 input-to-hidden weight으로 현재 time step의 input과 multiplication해줍니다. 마지막으로 해당 time step에 output을 구하려면 FC layer를 연결해주어 hidden-to-output weight에 현재 time step의 hidden state를 multiplication해 출력해주면 됩니다.

앞서 말씀드렸던 hidden state update 과정에서 전체 sequence가 같은 weight을 쓴다는 것, 이제는 이 weight이라는 것이 $W_{hh}, W_{xh}, W_{hy}$를 의미함을 알 수 있겠네요!

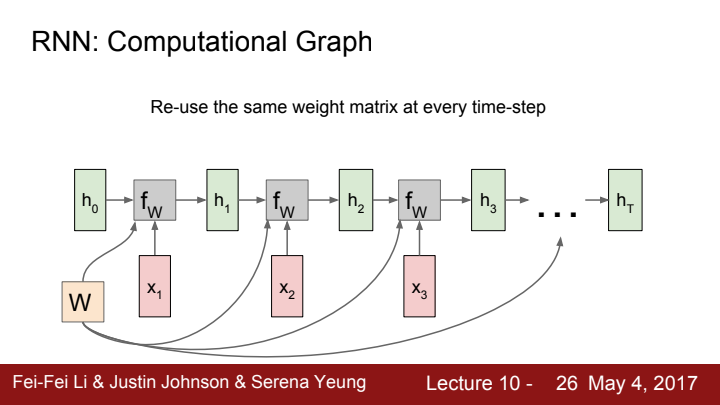
다음과 같이 말이죠.

앞서 말씀드렸다시피, 우리는 매 time-step마다 같은 weight matrix를 통해 hidden state를 update해 주게 됩니다.

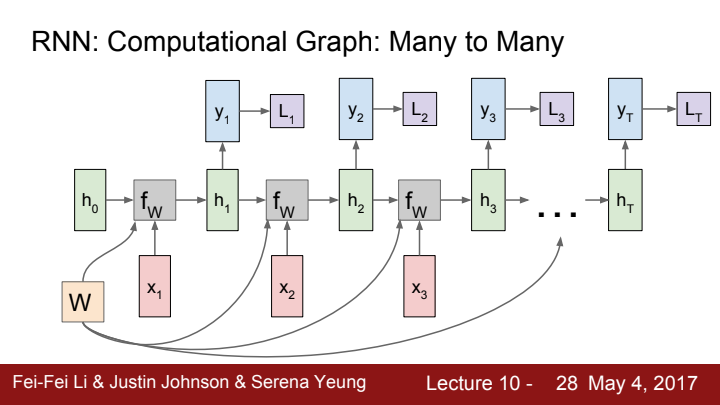
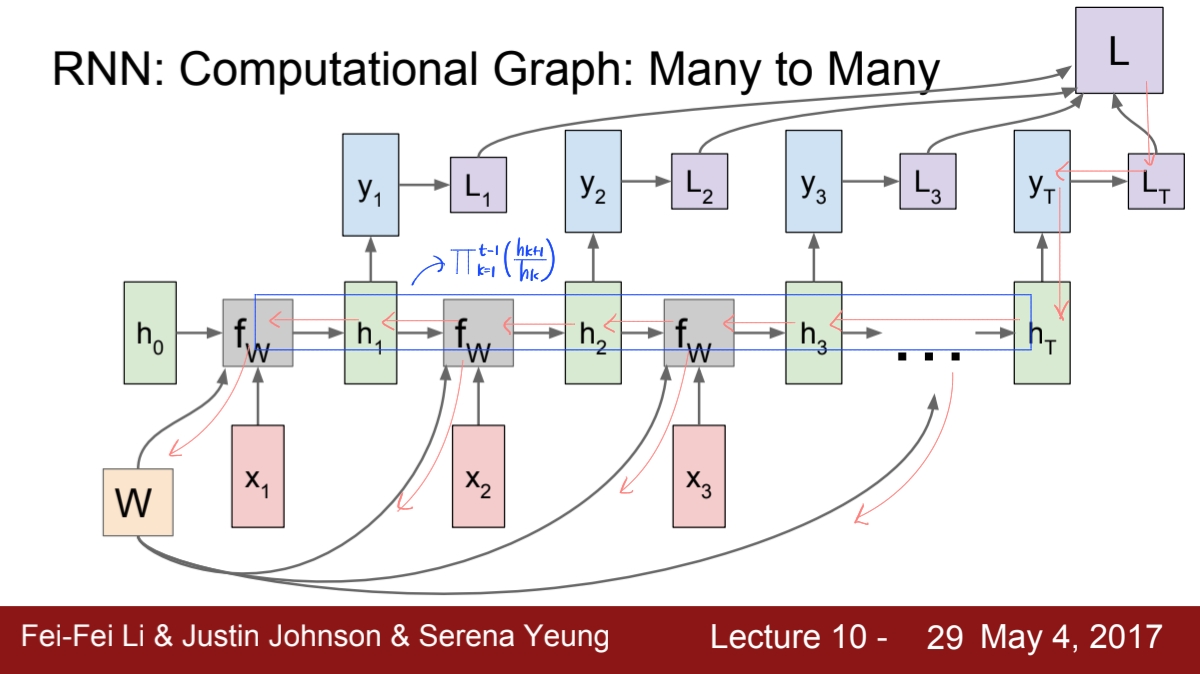
Many-to-Many process를 예시로 이어 설명해보도록 하겠습니다. 만약 매 time step마다의 ground truth가 존재한다면, 우리는 매 time step마다 output을 출력하고 그 output의 loss를 구해줄 수 있습니다.

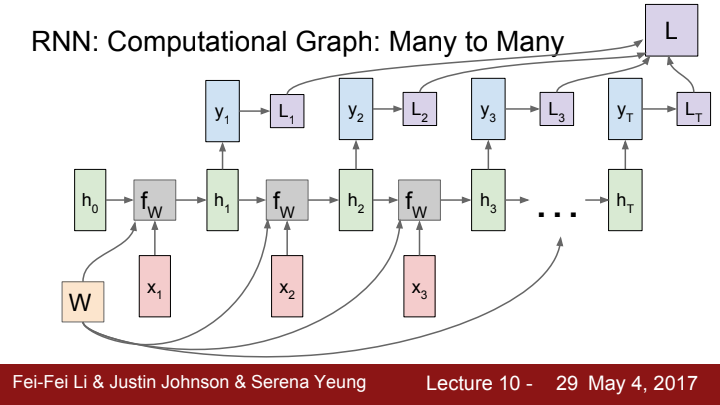
각 time step에서 구한 loss들을 모두 sum해 total loss를 구해줍니다. 이제 loss를 구했으니 backpropagation을 통해 Weight update를 해주어야겠죠? backprop을 위해선 loss에서의 gradient를 구해주어야 하는데, total loss는 각 time step에서의 loss들을 더한, 즉 add gate의 output이 되겠죠? 그렇기 때문에 우리는 backprop을 위해 우선 매 time step마다 local gradient를 계산한 뒤, 이 gradient를 모두 더해 total loss의 local gradient를 구할 수 있게 됩니다.
이 total gradient를 가지고 Weight matrix를 계산해주게 되는 것이죠! 왜 순차적인 데이터를 처리하는 모델을 이렇게 total gradient 하나만 가지고 계산하냐 물으신다면, 그 이유는 core cell에서 hidden state를 구하는데 쓰이는 weight은 매 time step 동안 동일한 weight을 사용하기 때문입니다!

조금 더 자세히 설명하자면, gradient flow는 다음과 같이 진행됩니다:

• 최종 손실에서의 역전파: 최종 손실 L부터 시작합니다. 이 손실은 모든 time step에서의 개별 손실 $L_1, L_2, L_3, ..., L_T$의 합입니다.
  L에서부터 각 time step의 출력 $y_1, y_2, y_3, ..., y_T$까지 역방향으로 그레디언트를 계산합니다.

• 각 time step에서의 역전파: 각 $L_T$에서 그레디언트는 두 경로를 통해 역전파됩니다.
  하나는 해당 time step의 출력 $y_T$를 생성한 직후의 계산으로 이어집니다($h \rightarrow y \rightarrow f_W \rightarrow W$ 로 이어지는 straight한 경로). 다른 하나는 $h_{T+1}$에서 $h_T$로 가는 경로압나더.

• 가중치 행렬에 대한 gradient 계산: 각 time step에서의 $f_W$를 통해 전파된 gradient는 가중치에 누적되어, total gradient를 형성합니다.

• total gradient 계산: 모든 time step의 gradient들이 적용된 후, 가중치 W에 대한 total gradient가 계산됩니다. 각 time step에서의 gradient가 더해져 가중치 W에 대한 총 업데이트를 결정합니다.

역전파 과정 중에, 각 time step에서의 $h_t$와 $y_t$로부터의 그레디언트는 이전 time step의 hidden state $h_{t-1}$로 전파됩니다. 이는 $h_t$를 계산할 때 $W_{hh}$를 사용하여 $h_{t-1}$에서 온 것이기 때문입니다. 그 결과, $W_{hh}, W_{xh}$에 대한 gradient가 시간에 거슬러 계산되고, 이 gradient들은 모든 time step에 걸쳐 합산되어 각 가중치의 업데이트를 결정합니다.

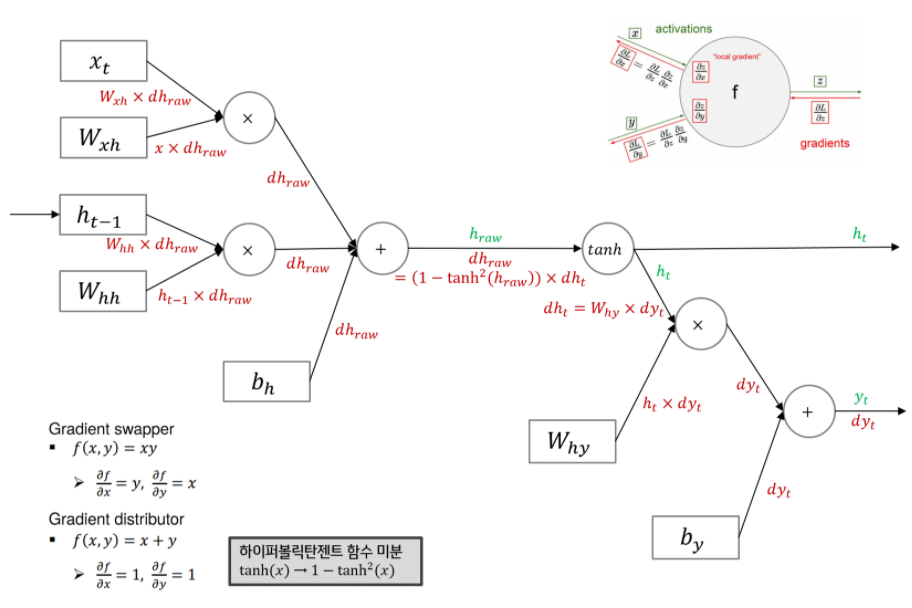
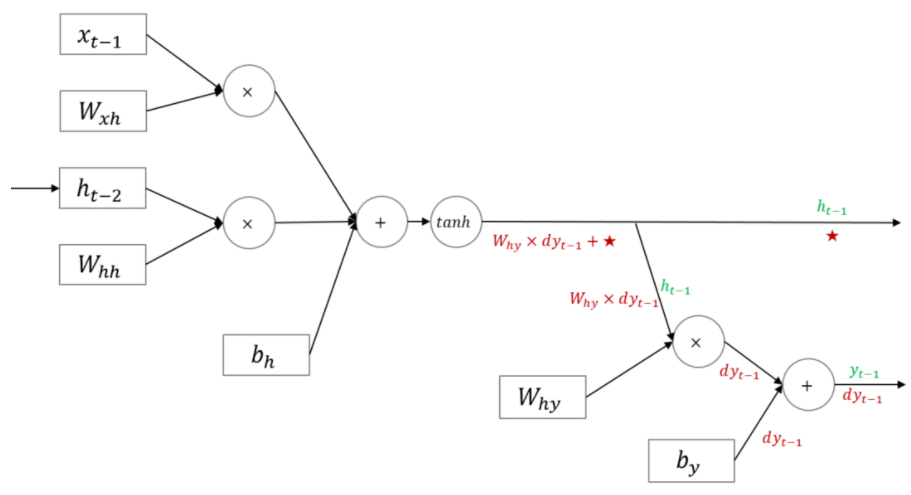
말로만 들으니 뭔가 이해도 안 되고 와닿지도 않아서, RNN의 Backpropagation 과정에 대해 구글링 해 자료를 긁어왔습니다. 첫 번째 그림이 $y$만을 통해 backpropagation을 수행하는 과정을 보여주고 있고, 두 번째 그림에선 $h_{t-1}$로부터의 upstream gradient값을(그림에선 별로 표시되었습니다) 더해 backpropagation을 수행하고 있습니다.

직접 수식 전개도 해보았습니다. 저는 첫 번째 방식으로만 논리를 전개해봤기 때문에 이후 배울 BPTT에 대한 내용이나 LSTM을 사용하는 이유인 vanilla RNN에서의 gradient flow 문제에 대해 이해가 잘 가지 않았습니다. 그러다가 RNN 모델의 foward pass 흐름의 역방향으로 화살표를 그려가며 수식을 전개해보니 이제야 이해가 좀 가더군요.

아마 제가 전개한 두 수식은 결과적으로 같은 값을 도출해 낼 것입니다. 아마도요..! 하지만 최적화 관점에서 보았을 때, 첫 번째 과정보다는 두 번째 과정이 훨씬 효과적일 것입니다. 계산하면서 발생하는 중간 결과들을 저장하여 다른 time step의 gradient 계산에 활용하기 더 편리한 구조이니 말이지요.

두 번째 수식대로 이해를 해보니, vanilla RNN이 깊이가 깊어질수록 gradient vanishing이나 exploding이 발생하기 쉽다는 말이 이해가 가는 것 같습니다! 이는 뒤에서 좀 더 상세히 설명토록 하겠습니다.

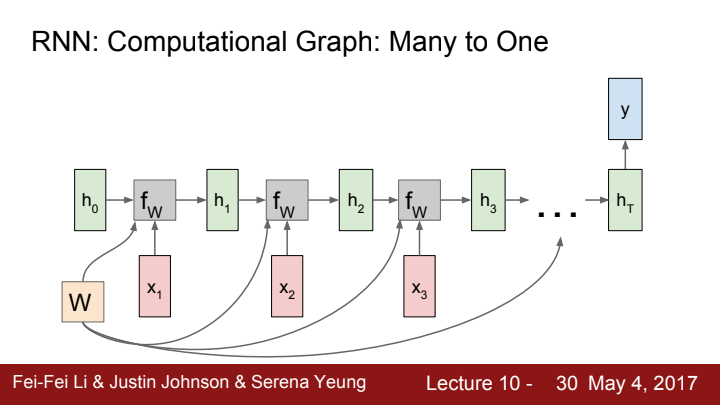
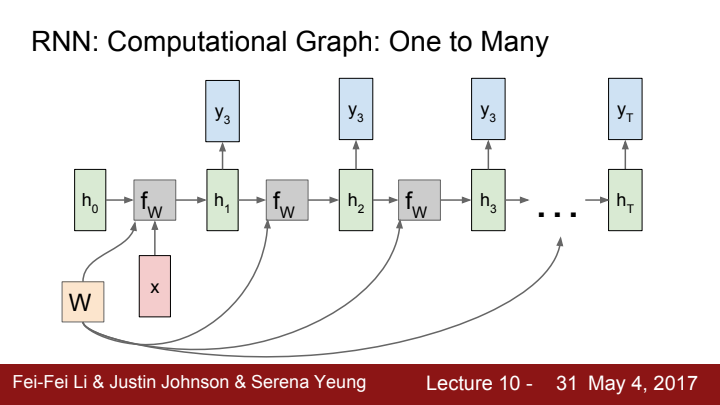
many-to-many 이외에도 many-to-one, one-to-many process에서도 RNN을 사용할 수 있습니다. one-to-many의 경우 input을 단 하나만 받기 때문에, 이 input은 initial hidden state를 초기화하는 데에 사용됩니다. 이후 time step부터는 input이 아닌 hidden state만으로 다음 time step의 hidden state를 update하기에 update에 필요한 함수가 더 이상 $tanh(W_{hh}h_{t-1}+W_{xh}x_t)$이 아니겠네요.

Sequence to Seqeunce (Seq2Seq)

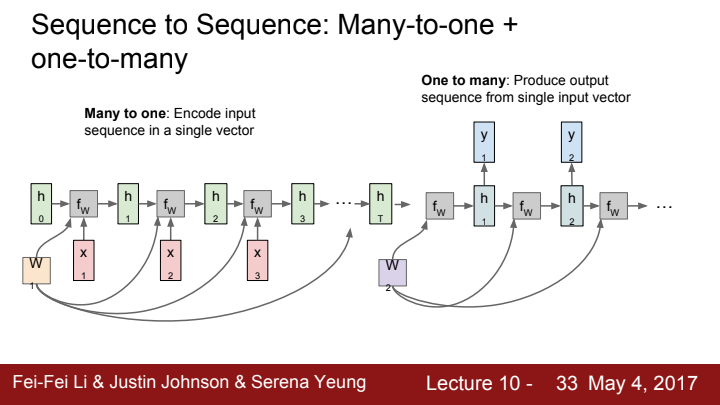
vanilla RNN을 활용한 모델인 Seq2seq에 대해 설명드리겠습니다. 본 강의에서는 그렇게 비중있게 해당 모델을 다루진 않았지만, 앞서 말씀드렸다시피 transformer 모델의 탄생 역사에서 큰 비중을 차지하는 모델이기에 그 원리를 간략하게라도 이해하고 계심이 좋을 것 같습니다.

seq2seq 모델은 many to one RNN + one to many RNN의 결합으로 구성되었습니다. 입력이 들어오는 many to one RNN 파트에서는 input sequence를 Encoding, 즉 하나의 단일 벡터로 축약시켜 줍니다. 이 벡터는 input sequence에 대한 context 정보를 함축하고 있죠. 이 벡터를 context vector 혹은 latent vector라고 합니다.

Encoding 과정을 거친 context vector가 one to many RNN으로 들어오게 되면, 이번엔 반대로 context vector의 'context'를 가지고 input sequence에 대한 적절한 output sequence를 생성해냅니다. 즉 one to many 파트는 말 그대로 decoding을 맡는다고 볼 수 있습니다.

RNN Example: Character-level Language Model

RNN의 구조에 대해 배워보았으니. RNN을 활용한 간단한 task 중 하나를 예시로 들어 설명해보도록 하겠습니다. RNN은 input character를 가지고 sequence 내에서 다음 character를 예측해내는 character level language modeling을 할 수 있습니다.

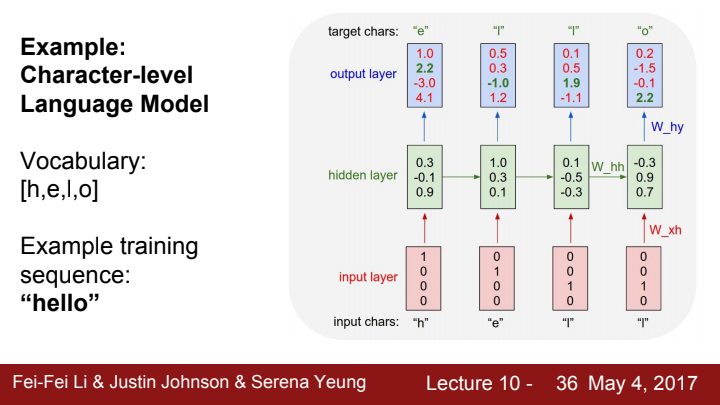
training 과정에서 우선 다음과 같이 hello라는 target sentence를 모델이 생성할 수 있도록 지도학습을 시켜줄 수 있습니다. hello라는 단어의 character들을 리스트로 뽑아보면 [h,e,l,o]가 됩니다. 우리는 이 character들을 RNN model에 입력으로 넣어 다음 character를 target으로 설정해주고 모델을 training시켜줄 수 있습니다.

특이하게 입력 벡터가 softmax vector의 형태가 아닌 one hot vector의 형태임을 확인할 수 있습니다. 여기서 one hot vector란 표현하고자 하는 character나 word의 index에는 1, 나머지 index에는 0의 값이 들어간 vector를 의미합니다. 제가 자연어 처리 분야에 대해서는 문외한이라 확신 드리긴 어렵지만, 자연어 처리에서 character나 word를 표현할 때 one hot vector를 많이 사용하는 것으로 알고 있습니다.

왜 one hot vector를 사용하는 것일까요? 그 이유는 크게 두 가지를 생각해 볼 수 있는데, 만약 train 때 들어온 data와 test 때 들어온 data가 매우 다르다면, softmax vector 사용 시 결과값이 말 그대로 쓰레기가 나올 것입니다.

두 번째로, vocabulary가 늘어날수록 softmax vector의 경우 필연적으로 vector가 dense해질 수 밖에 없습니다. 이런 dense vector를 사용하면 계산하기가 많이 어렵습니다. 그럴 바에 차라리 sparse(=대부분의 값이 0)하면서도 직관적인 one hot vector를 사용하는 것이 계산에 용이하다는 것입니다.

training 과정은 쉽고 직관적이죠? 하지만 test time에서는 어떻게 해야 할까요?

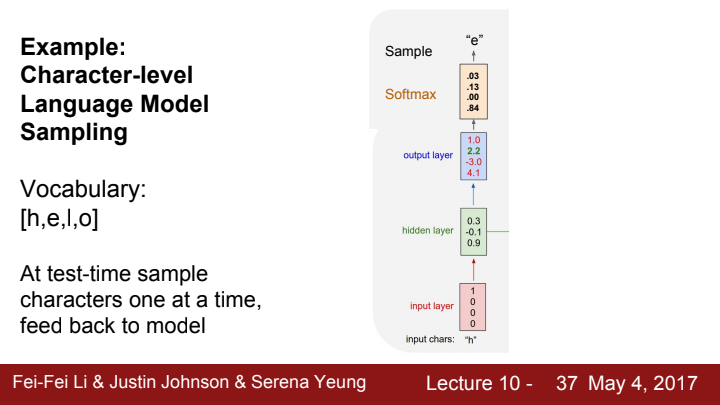
test time에서 모델을 평가하기 위해선, 우리는 sampling 기법을 사용해주어야 합니다. 이에 대해 설명해 보도록 하겠습니다.

원래 우리는 training time에선 output layer의 값을 그대로 출력으로 삼아주었다는 것을 기억할 수 있습니다. 하지만 test time에선, 각 character들에 대한 output score들을 가지고 softmax함수를 적용해 각 character에 대한 확률분포를 구해줍니다. 그리고 이 확률분포를 기반으로 character들 중 하나를 임의로 sampling 해 해당 time step의 output으로 삼아줍니다.

이는 모델이 한 character에 대해 고정된 다음 character, 전체적으로 단 하나의 sequence만을 예측하는 것이 아닌, 다양한 reasonable output sequence들을 예측할 수 있도록 하기 위함입니다. 실제로 위 그림에서 output score들을 기반으로 생각해본다면, 'h' 다음으로 와야 할 단어는 'e'가 아닌 'o'가 되었을 것입니다. 만약 그랬다면 우리는 이 모델에게서 'hello'라는 단어를 output으로 얻을 수 없게 되었겠죠?

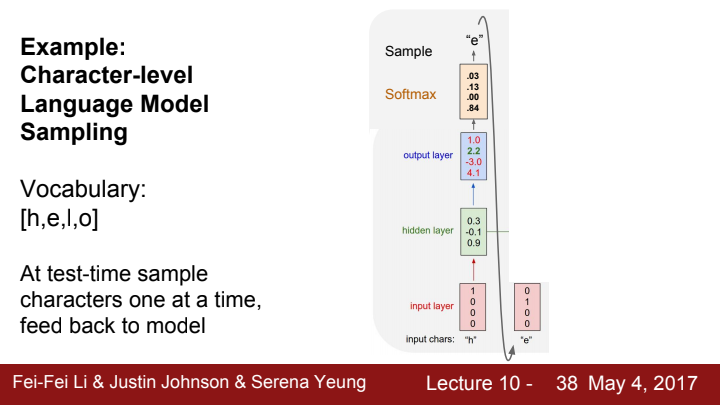
이러한 과정을 거쳐 특정 time step에서 sampling을 통해 추출된 output은 다음 time step에 feedback되어 input으로 들어가게 됩니다.

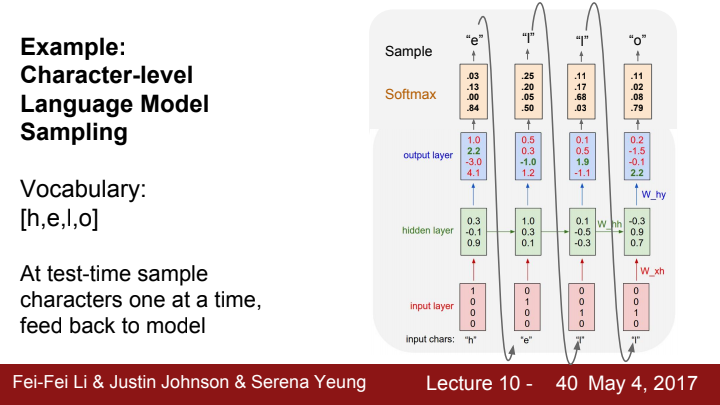
이런 식으로 말이죠!

Backpropagation through time (BPTT)

RNN의 backpropagation 과정인 BPTT에 대해 일전에 자세히 다뤘었죠?

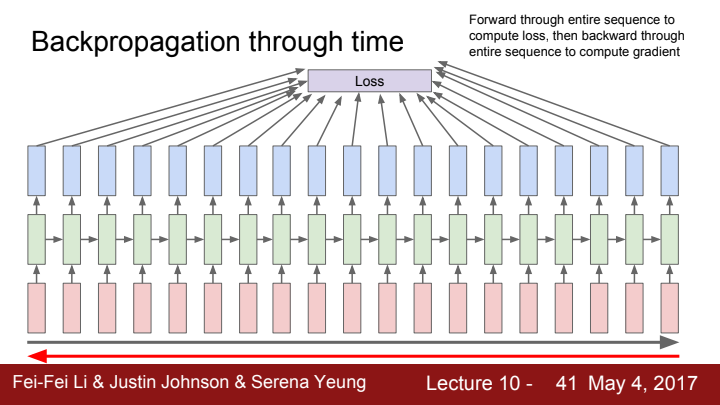
우리는 매 time step마다 loss를 계산해서 total loss를 계산했고, 이 total loss를 기반으로 각 time step의 local gradient를 모두 계산해 이를 더해줌으로써 total gradient를 계산할 수 있었습니다. 이는 sequence의 time step이 매우 짧다면 문제가 없겠지만, sequence의 길이가 매우 길어진다면 계산 과정에 큰 어려움이 생길 수 있습니다. 마치 CNN의 Full batch Gradient Descent처럼 말이죠. 계산이 매우 느려질 것이고 컴퓨팅 자원의 비용이 매우 비싸질 것입니다.

우리는 Full batch GD의 문제점을 해결하기 위해 데이터를 minibatch로 나누어 SGD를 수행했었죠? 이와 비슷하게 RNN에서도 sequence data를 부분적으로 나누어 계산을 수행함으로써 비용을 줄이고 계산 속도를 향상시킬 수 있습니다. 이 방법을 Truncated BPTT라고 부릅니다.

Truncated BPTT

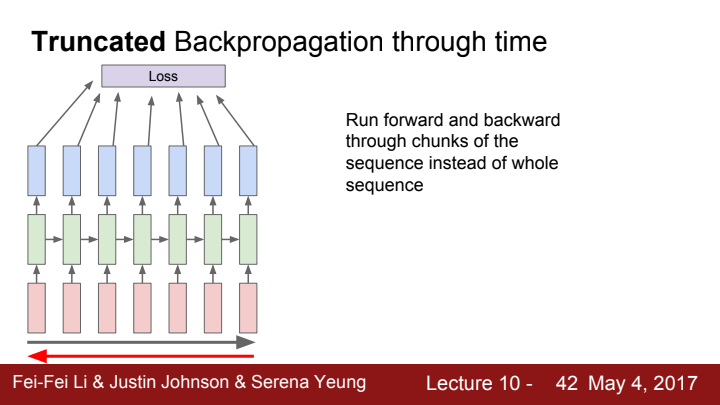
우선 backpropagation을 위해선 forward pass 과정을 거쳐주어야겠죠? 우리는 이 forward pass와 backpropagation을 chunk 단위로 수행해줍니다. 여기서 chunk란 CNN의 minibatch와 비슷한 개념이라고 생각하시면 됩니다. 말 그대로 내가 정해준 number of time step인 것이죠. 위의 자료를 보시면 7 time step으로 구성된 chunk 단위로 backpropagation을 해주는 것을 확인할 수 있습니다.

이런 truncated BPTT의 장점은 계산효율이 그냥 BPTT에 비해 훨씬 좋다는 점입니다. 하지만 딱 봐도... 단점이 있음이 느껴지지 않나요? truncated BPTT는 매 업데이트의 결과가 short-term dependant합니다. 즉 chunk 1개에 대한 결과에만 의존한다는 뜻이죠. 즉 truncated BPTT를 통해 한 epoch동안 update 결과는 각 chunk들에 의존적인 local 최적값들의 조합으로 도출되었기 때문에, 해당 결과가 global한 최적값, 즉 sequence 전체에 대한 최적값이라는 보장이 없는 것입니다.

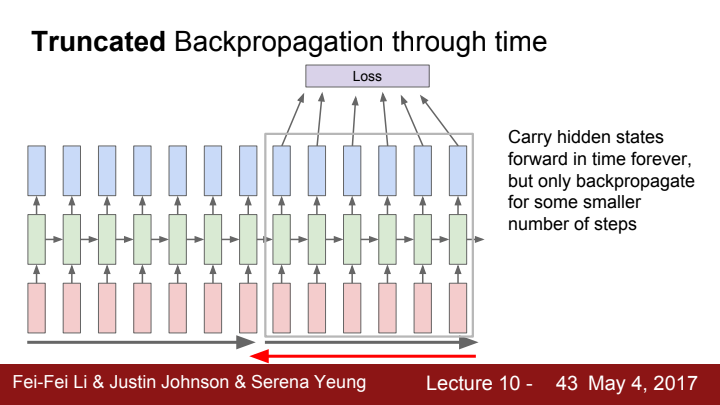
특이한 점은 forward pass 과정에서 이전 hidden state 값을 받아와 수행해줍니다. 사실 당연한 이야기죠? 8번째 time step의 hidden state를 계산하기 위해선 반드시 이전 chunk에 포함된 7번째 time step의 hidden state 값이 필요하기 때문에...

하지만! 당연히 backpropagation에선 해당 chunk까지만 backward의 path가 뻗어나가도록 수행해줍니다. 즉 해당 chunk까지만 backpropagation을 수행해주는 것입니다. 이것도 당연하죠? 이름에서 말 그대로 chunk 단위로 truncated(잘라낸) BPTT를 수행해줘야 하니까요.

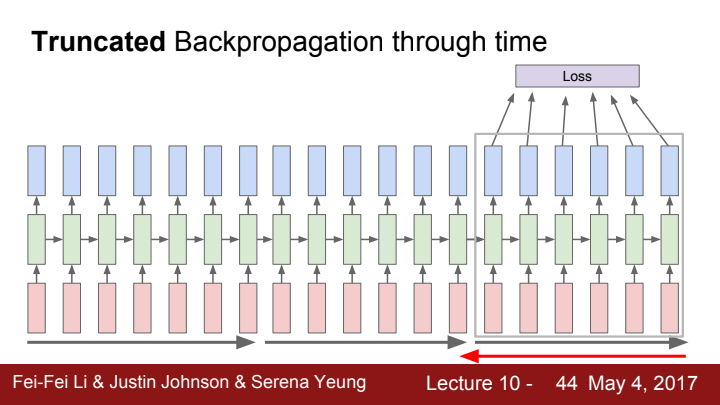
이렇게 쭉쭉...전체 sequence에 대한 작업이 끝날때까지 이어가줍니다!