B-트리(B-Tree)란? B트리 탐색, 삽입, 삭제 과정

Chan Young Jeong·2023년 3월 18일

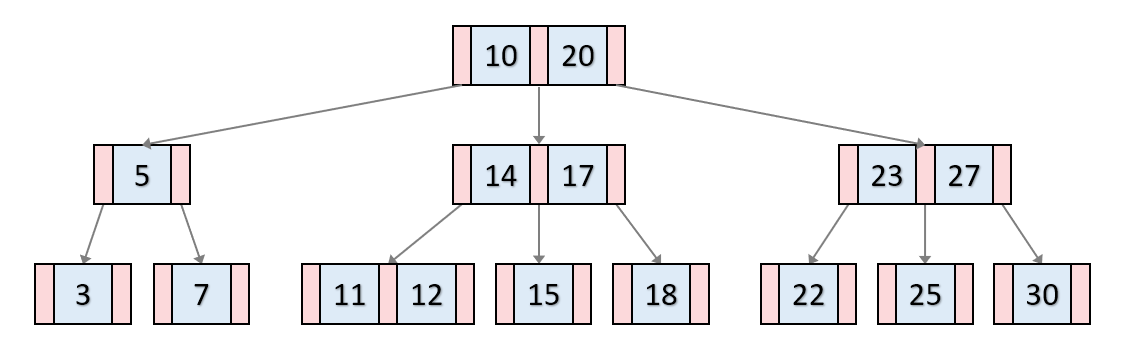
B-트리란?

B-트리(B-tree)는 데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로, 이진 트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다.

B-트리의 특징

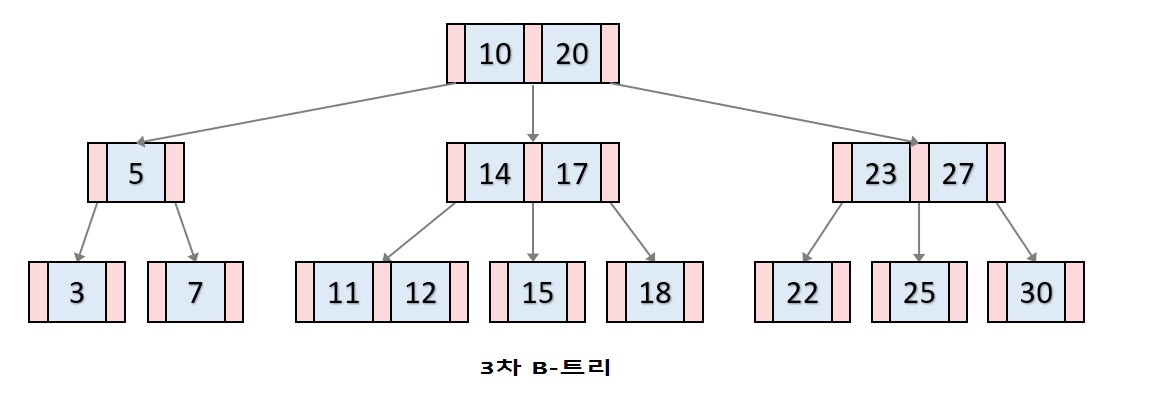
B트리는 이진트리와 다르게 하나의 노드에 많은 수의 정보를 가질 수 있습니다. 최대 M개의 자식을 가질 수 있는 B-트리를 M차 B-트리라고 합니다.

노드는 최대 M개의 자식 노드를 가질 수 있다.
ex) 3차 B-트리라면 최대 3개의 자식 노드를 가질 수 있다.
노드에는 최대 M-1개의 KEY를 가질 수 있다.
ex) 3차 B-트리라면 최대 2개의 KEY를 가질 수 있다.
각 노드는 최소 ⌈M/2⌉개의 자식 노드를 가진다. (루트 노드와 leaf 노드 제외)
ex) 3차 B-트리라면 각 노드는 최소 2개의 자식 노드를 가진다.
각 노드는 최소 ⌈M/2⌉-1개의 키를 가진다. (루트 노드 제외)
ex) 3차 B-트리라면 각 노드는 최소 1개의 키를 가진다.
internal 노드의 KEY가 x개라면 자녀 노드의 수는 언제나 x+1 개다.

-> 노드가 최소 하나의 KEY는 가지기 때문에 몇 차 인지에 상관없이 internal 노드는 최소 두개의 자녀는 가진다.
( m이 정해지면 root노드를 제외하고 internal 노드는 최소 ⌈M/2⌉개의 자녀 노드를 가질 수 있게 된다. )

노드에 KEY들은 항상 정렬된 상태로 저장된다.

B 트리 데이터 삽입

추가는 항상 leaf 노드에 한다.
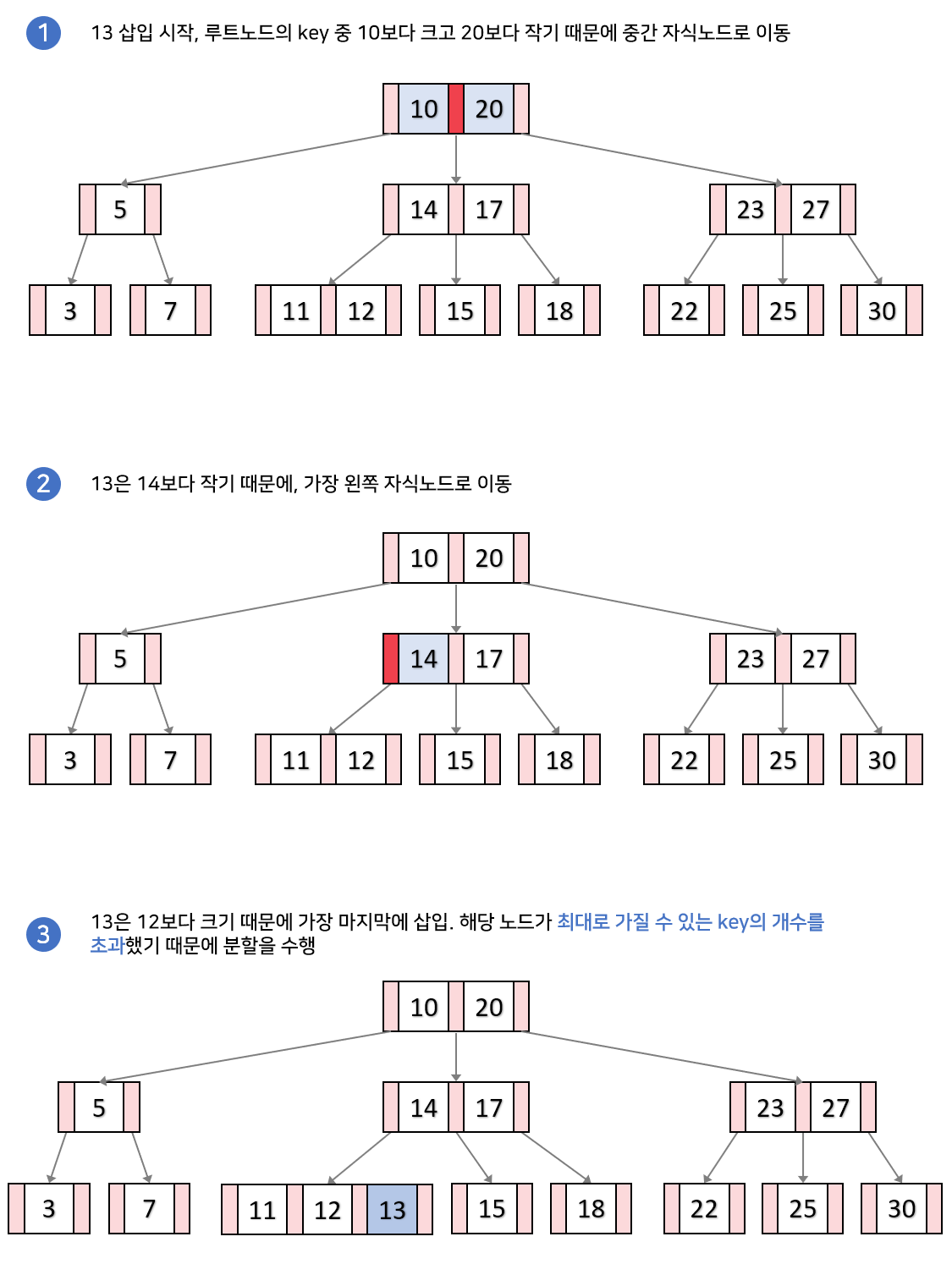
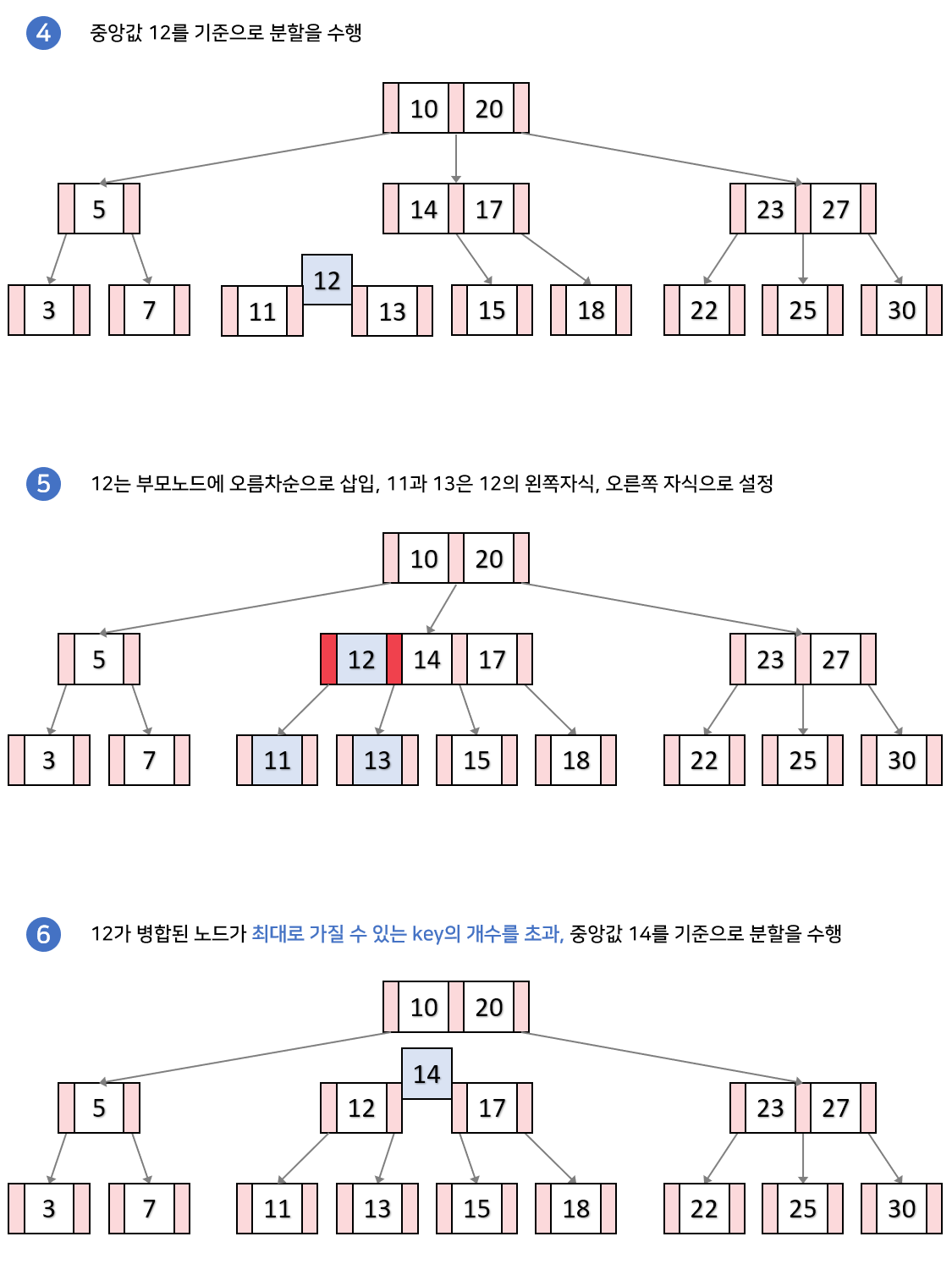
노드가 넘치면 가운데(Median) key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.

=> 노드가 넘친다?
ex) M차 B트리에서 각 노드는 최대 M-1개의 KEY를 가질 수 있는데, 데이터를 삽입하는 과정에서 이를 위반한 것.

구체적인 삽입 과정은 다음과 같다.

1. 트리가 비어있다면 루트 노드를 할당하고 K를 삽입한다.
2. 트리가 비어있지 않다면, 데이터를 넣을 적절한 리프 노드를 탐색한다.
3. 리프 노드에 데이터를 넣고 리프 노드가 적절한 상태에 있다면 종료한다.
4. 리프 노드가 부적절한 상태에 있다면 분리한다.

Case1. 분할이 일어나지 않는 경우

리프노드가 넘치지 않았다면, 오르차순으로 k를 삽입한다.

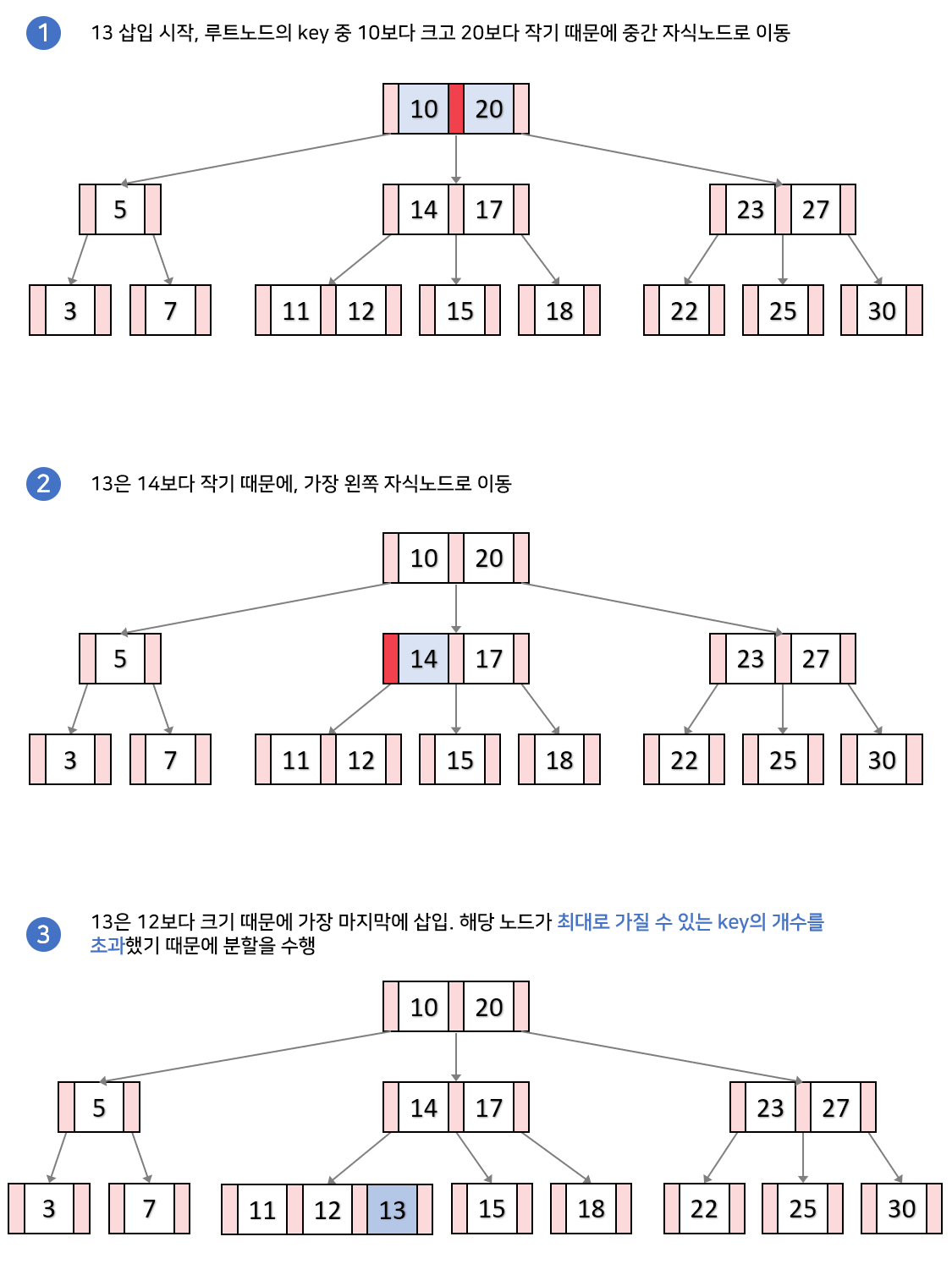
Case2. 분할이 일어나는 경우

만일 리프노드에 key노드가 가득 찬 경우, 노드를 분할해야 합니다.

노드가 넘치면 가운데(Median) key를 기준으로 좌우 key들을 분할하고 가운데 key는 승진한다.

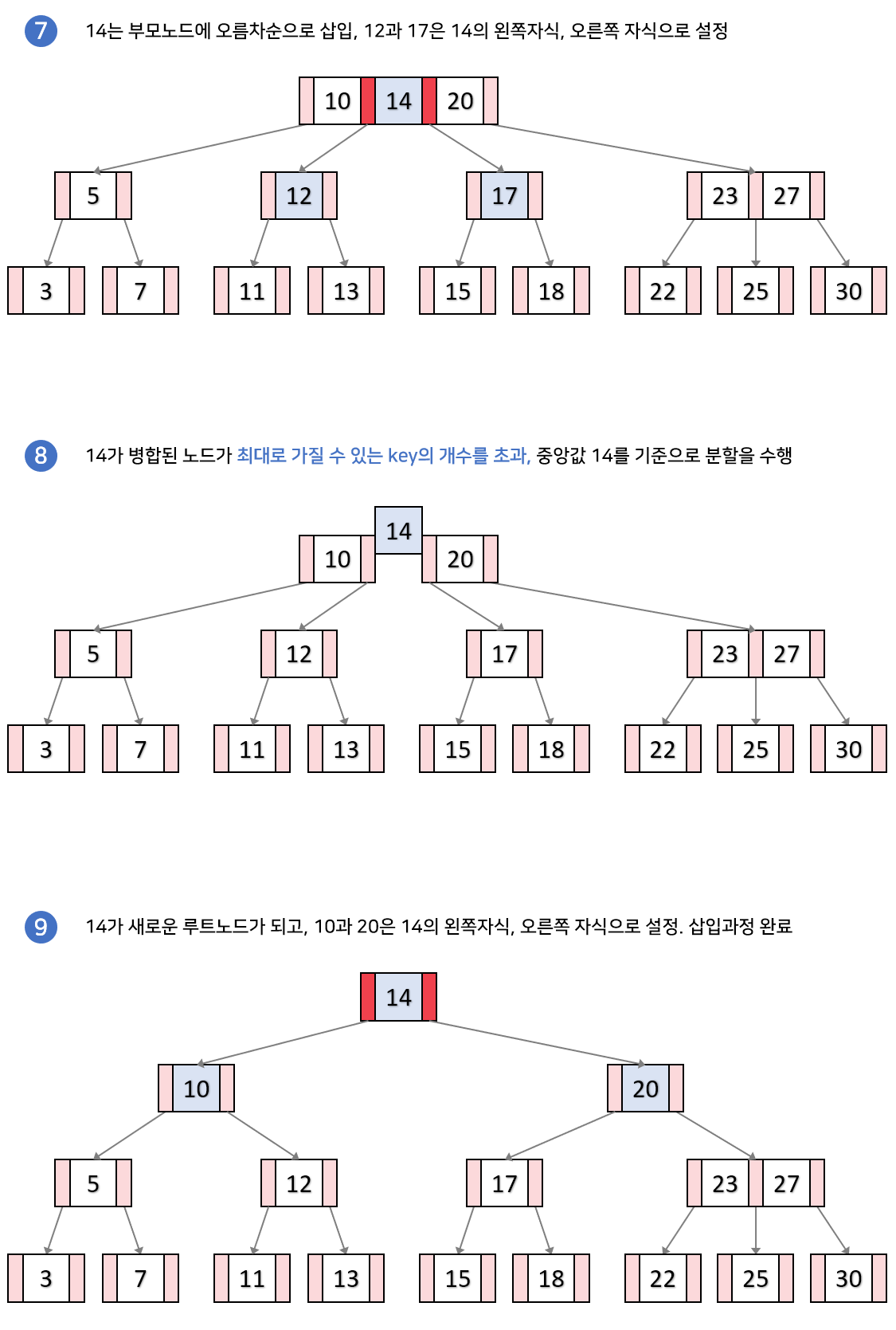
B 트리 데이터 삭제

삭제도 항상 leaf 노드에서 발생
삭제 후 최소 key 수보다 적어졌다면 재조정한다.
각 노드는 최소 ⌈M/2⌉-1개의 키를 가진다. (루트 노드 제외)

재조정 과정
1. key 수가 여유있는 형제의 지원을 받는다.
2. 1번이 불가능하면 부모의 지원을 받고 형제와 합친다.
3. 2번 후 부모에 문제가 있다면 거기서 다시 재조정한다.

Case1. 리프노드에서 삭제하고 재조정 할 필요 없는 경우

삭제하고 끝.

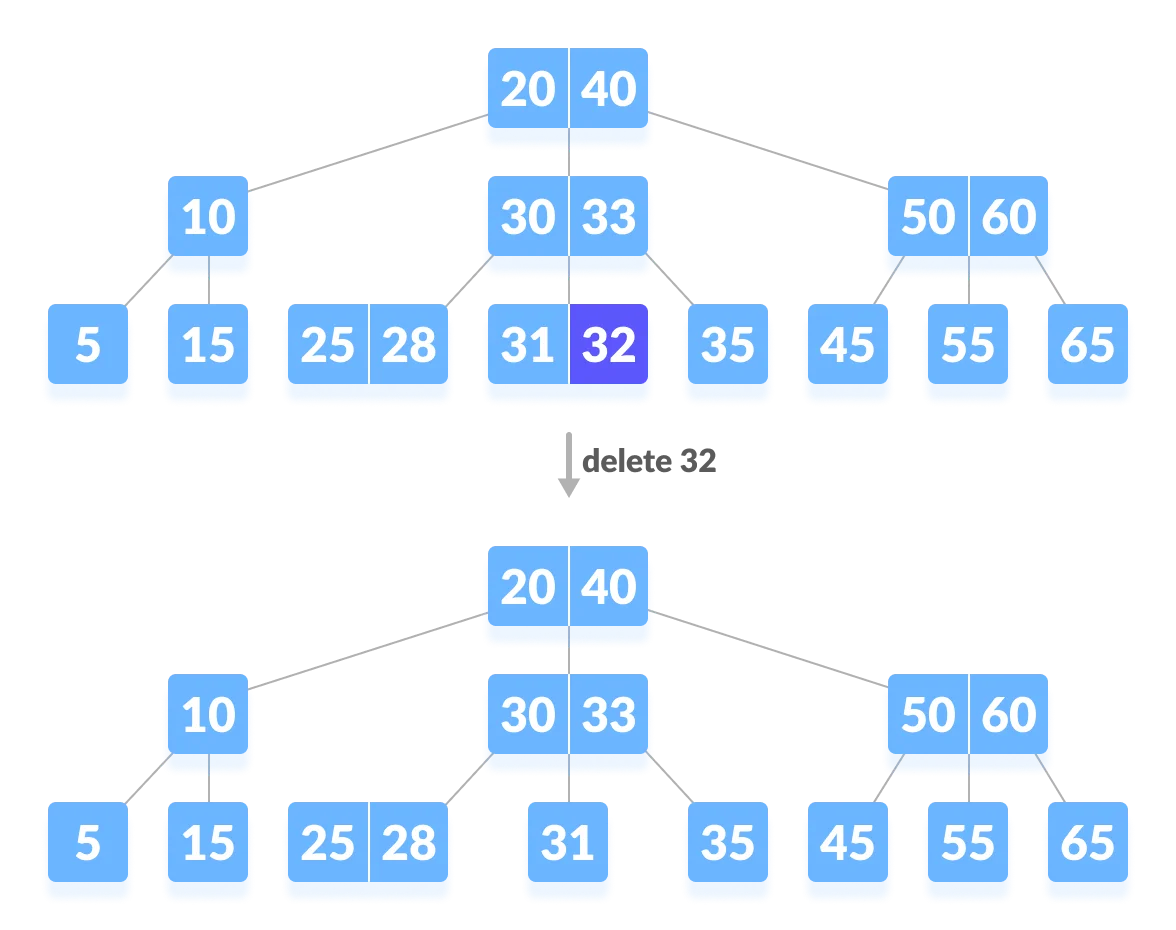
Case2-1. 리프노드에서 삭제하고 재조정 해야하는 경우

key 수가 여유있는 형제의 지원을 받을 수 있는 경우.

① 31을 삭제하면 최소한의 키수보다 작아지기 때문에 재조정을 해야한다.
② 1. key 수가 여유있는 형제의 지원을 받는다.
먼저 동생(왼쪽에 있는) 노드를 보면 키가 25,28로 여유가 있기 때문에 동생노드로 부터 키를 지원 받는다. 바로 28로 옮기는 것이 아니라 B트리의 속성에 맞게 28은 부모노드로 옮기고 30을 내린다.

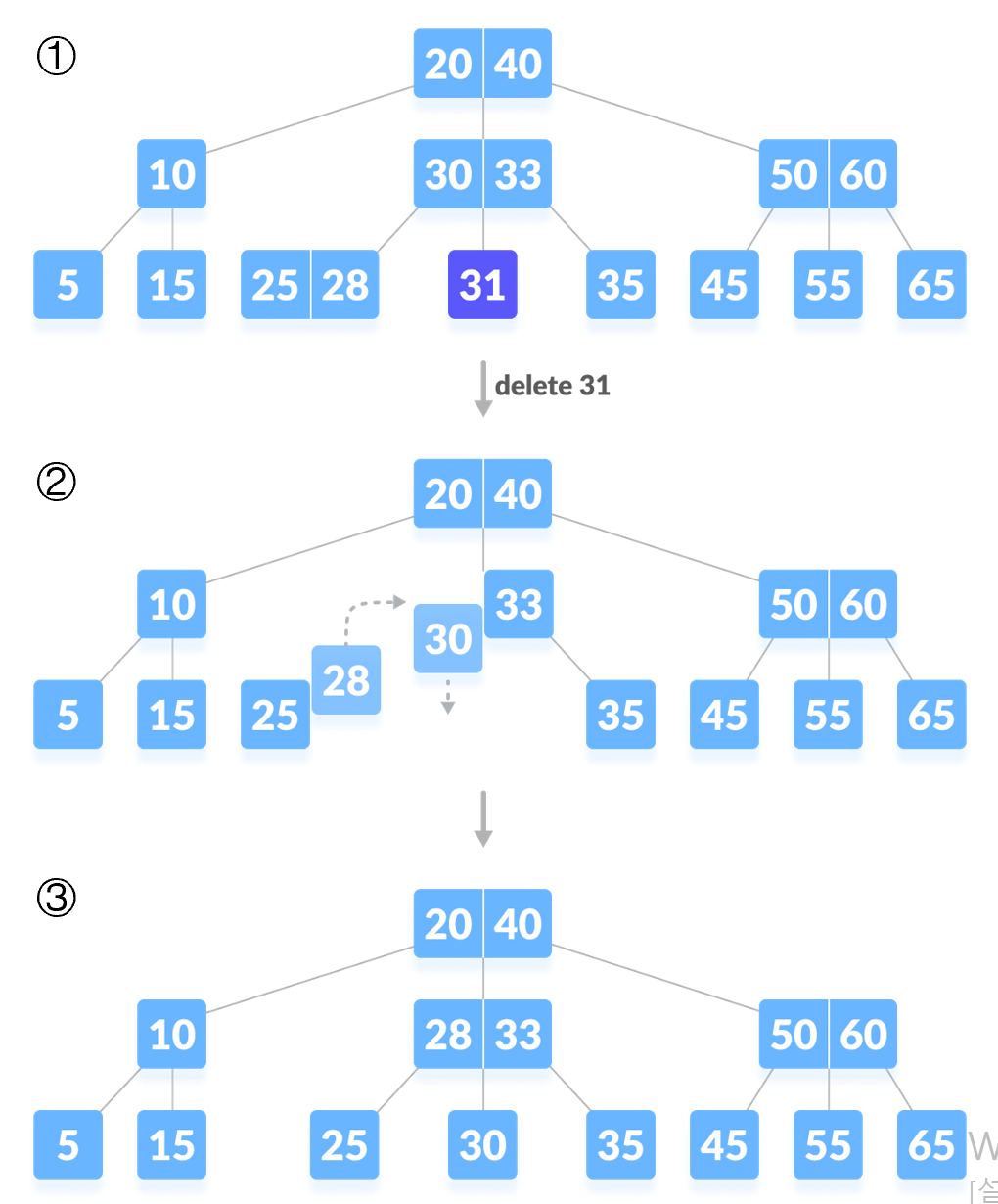
Case2-2 리프노드에서 삭제하고 재조정 해야하는 경우

key 수가 여유있는 형제의 지원을 받을 수 없는 경우에는 부모의 지원을 받고 형제와 합친다.

부모로부터 지원 방법
2.1 동생이 있으면 동생과 나 사이의 KEY를 부모로 부터 받는다
-> 그 KEY와 나의 KEY를 차례대로 동생에게 합친다.
-> 나의 노드 삭제한다.

2.2 동생이 없으면 형과 나 사이의 KEY를 부모로 부터 받는다.
-> 그 KEY와 형의 KEY를 차례대로 나에게 합친다.
-> 형의 노드를 삭제한다.

① 30을 삭제하면 최소한의 키수보다 작아지기 때문에 재조정을 해야한다.
② 1. key 수가 여유있는 형제의 지원을 받는다.
-> 양 옆에 있는 형제 노드 또한 각 각 25 , 35로 최소한의 키의 개수를 가지고 있기 때문에 지원 받을 수 없다.

2. 1번이 불가능하면 부모의 지원을 받고 형제와 합친다.

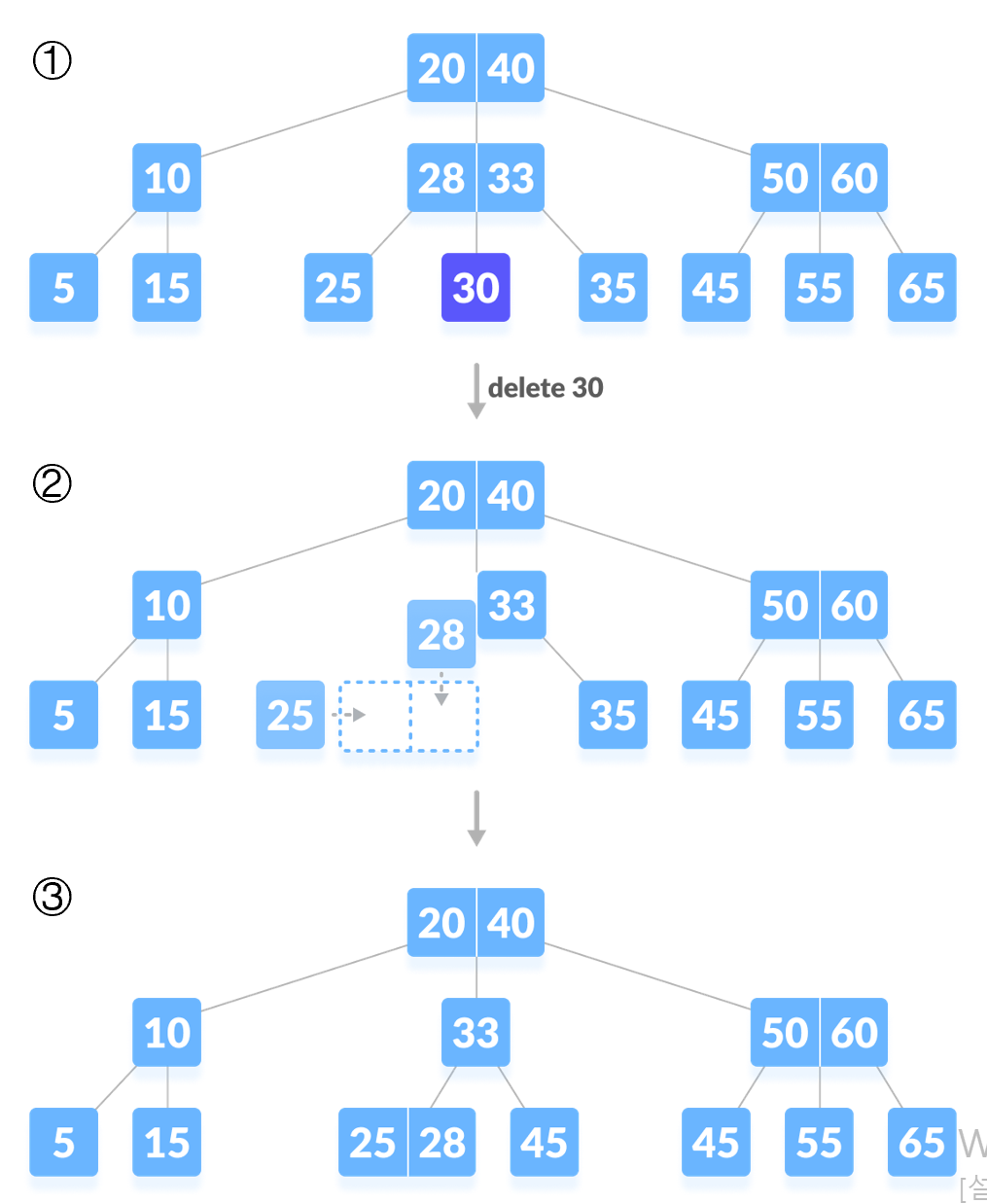
Case2-3 리프노드에서 삭제하고 재조정 해야하는 경우

재조정 2번 진행 이후 부모에서도 문제가 발생하여 거기서 다시 재조정 진행

3.1 부모가 ROOT 노드가 아니라면
-> 그 위치에서 부터 다시 1번부터 재조정 진행

3.2 부모가 ROOT 노드고 비어있다면
-> 부모 노드를 삭제한다.
-> 직저에 합쳐진 노드가 ROOT 노드가 된다.

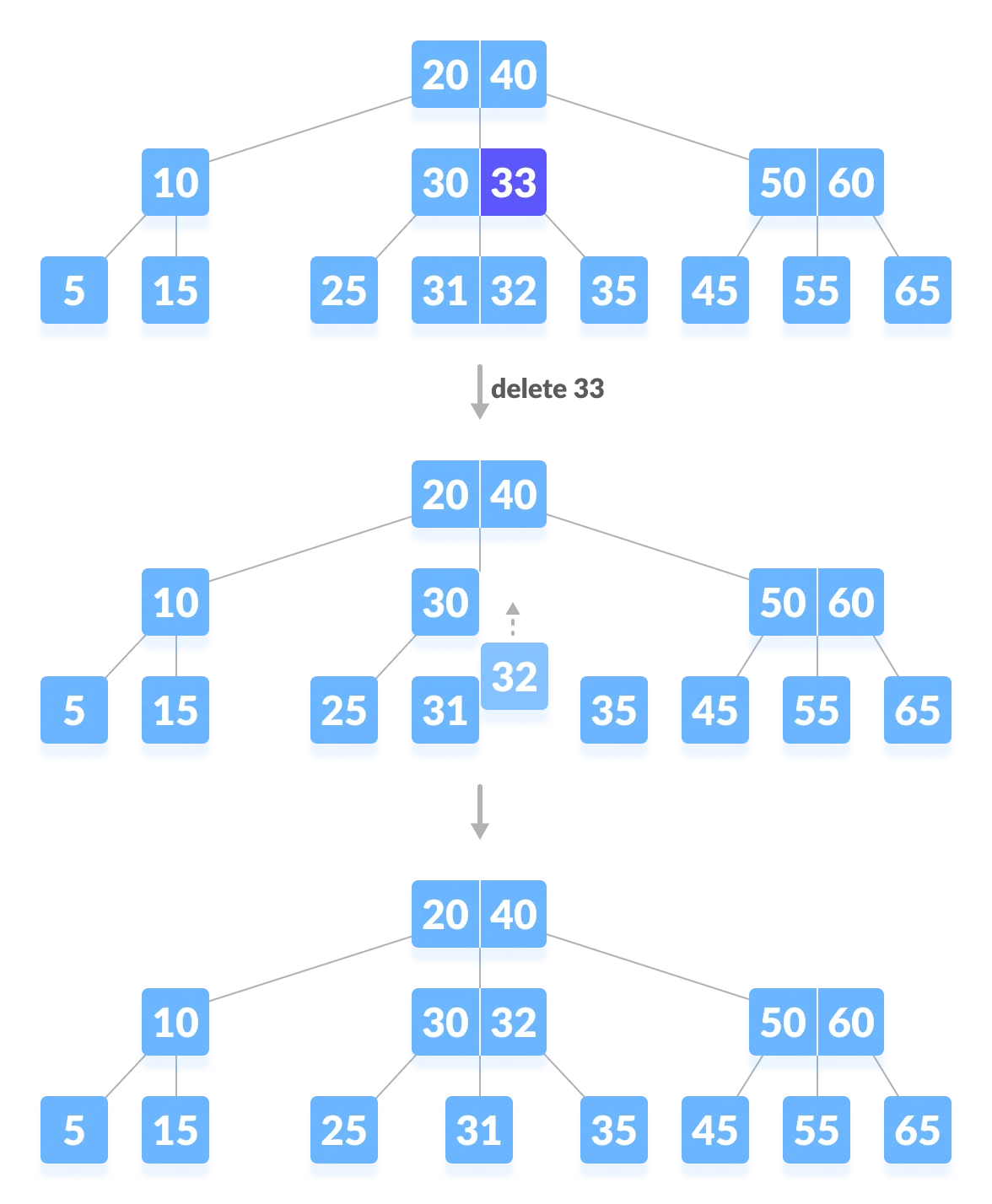
Case3 internal 노드에서 데이터 삭제하는 경우

internal 노드에 있는 데이터를 삭제하려면 leaf노드에 있는 데이터와 위치를 바꾼 후 삭제한다. -> 이후에는 Case2와 동일하게 진행.

어떤 leaf노드에 있는 데이터와 바꿀것인가?
삭제할 데이터의 선임자나 후임자와 위치를 바꿔준다.
※ 선임자(predecessor) : 나보다 작은 데이터들 중 가장 큰 데이터
※ 후임자(successor) : 나보다 큰 데이터들 중 가장 작은 데이터

① 33을 삭제할 때 , 33은 리프 노드가 아니기 때문에 33의 선임자를 찾는다. 33의 선임자는 32이기 때문에 32와 위치를 바꾸고 삭제를 진행한다.