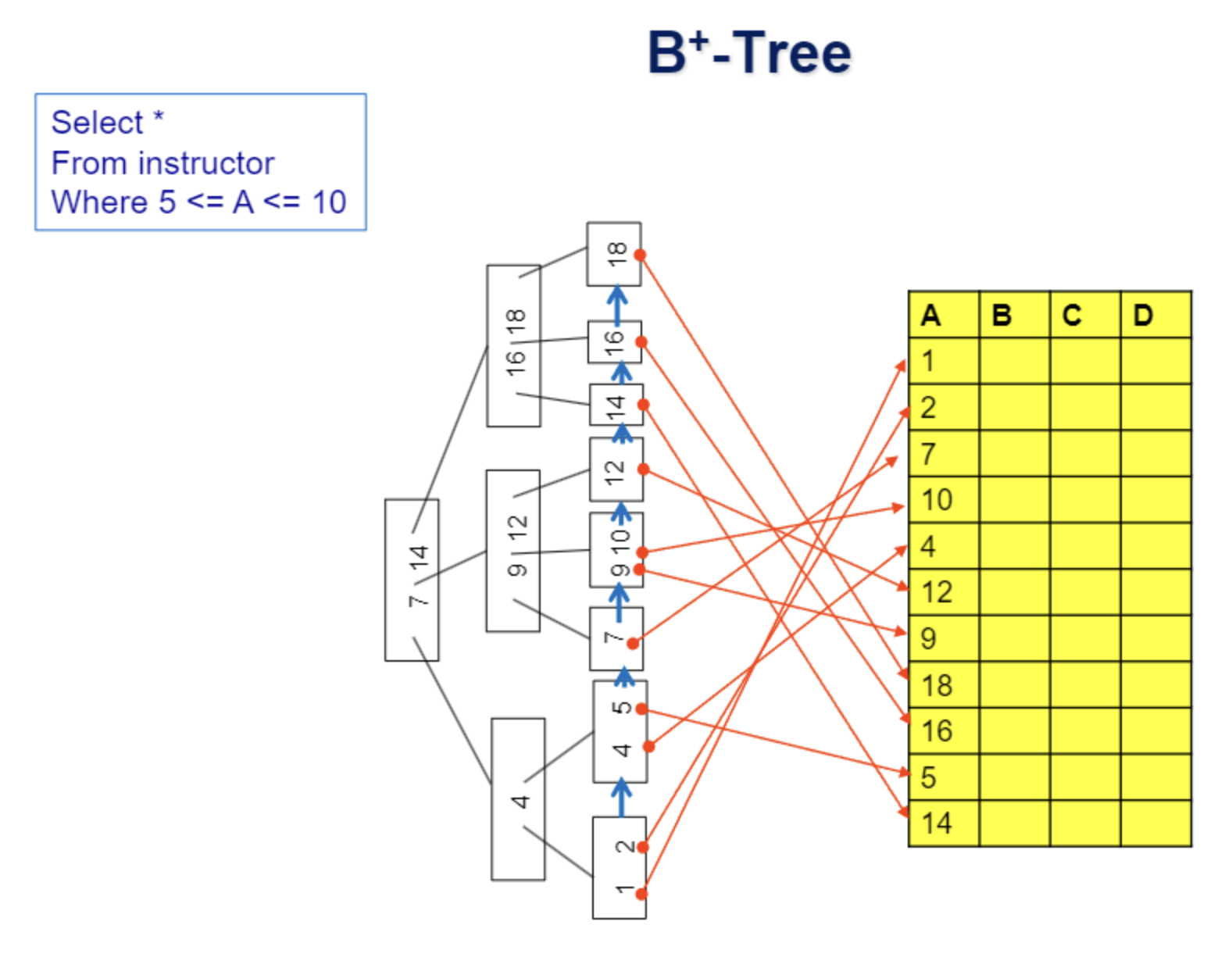
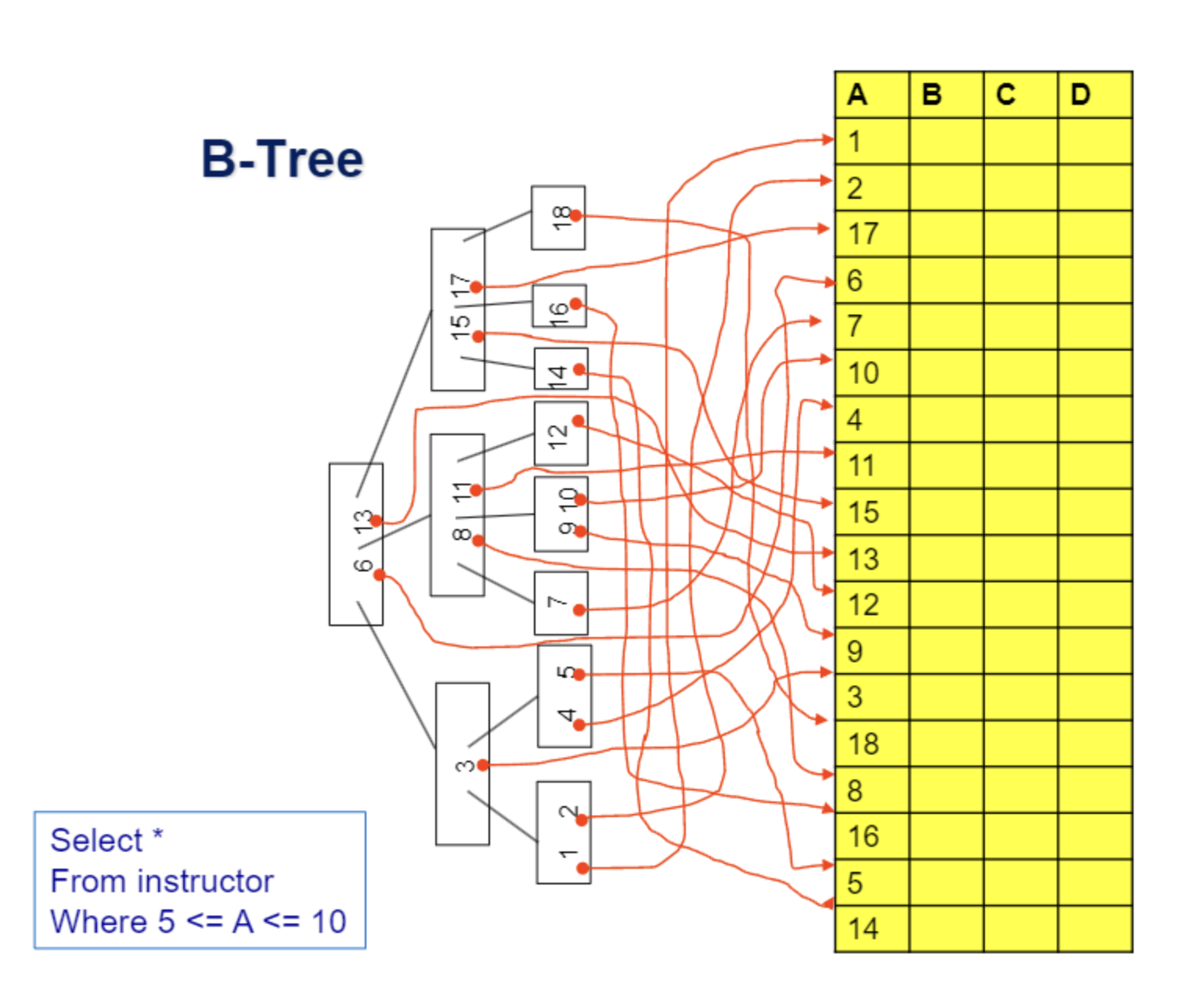
B+ Tree Index

B+ tree index는 데이터베이스에서 사용되는 인덱스의 일종으로, 효율적인 검색과 정렬을 위해 사용됩니다.

B+ 트리 인덱스는 다분기(Multiway) 트리의 일종으로, 각 노드에는 여러 개의 키 값이 저장됩니다. B+ 트리 인덱스는 트리의 높이를 줄이기 위해 많은 수의 키 값을 가진 노드를 사용합니다. 이를 통해 데이터베이스에서 매우 빠른 검색 및 삽입/삭제 연산을 수행할 수 있습니다.

또한 B+ 트리 인덱스는 멀티레벨 인덱스의 일종으로, Leaf node는 dense index의 역할을 하고 Inter node는 Leaf Node를 관리하는 sparse index 역할을 한다.

B+ 트리 인덱스는 데이터를 정렬된 상태로 유지하며, 범위 검색(Range Query)에도 매우 효율적입니다. 또한 B+ 트리 인덱스는 순서를 유지하고, 병렬 처리에 적합합니다. 이로 인해 데이터베이스의 성능을 크게 향상시킬 수 있습니다.

※ B+ tree index가 노드 단위로 데이터를 저장하고, 각 노드가 독립적인 키 값을 가지고 있기 때문입니다. 따라서 B+ tree index를 사용하면 데이터베이스의 병렬 처리 성능을 향상시킬 수 있습니다.

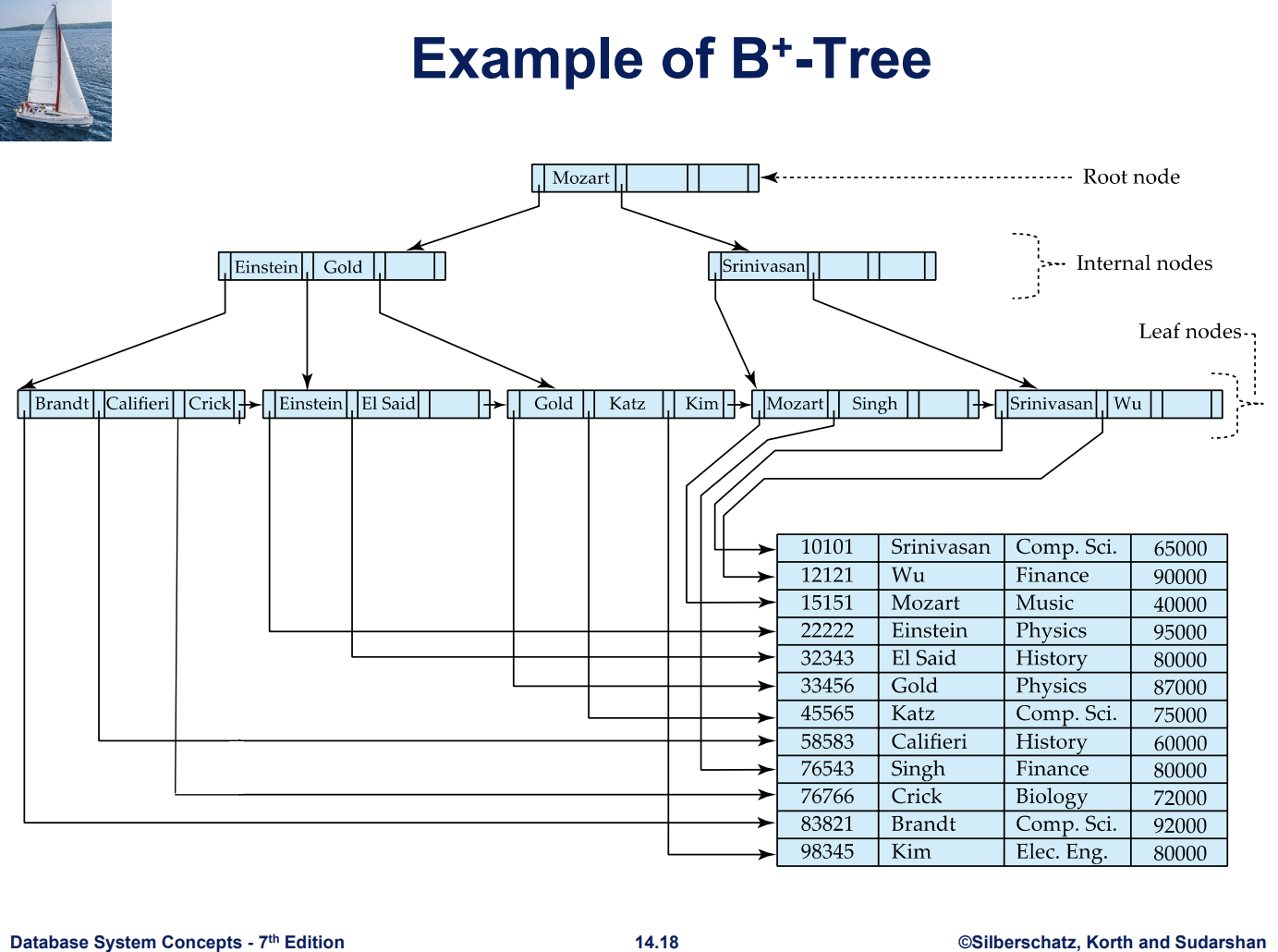
Inter Node는 split value와 하위 노드 포인터로 이루어져 있다. 그리고 Leaf Node는 search key와 레코드로의 포인터가 존재한다. 레코드 포인터에는 어느 파일 식별자, 블록 식별자, 슬롯 식별자 같은 정보가 포함될 수 있다.

B+ Tree Index Properties

1. 균형 요건
   Root 노드부터 모든 Leaf node까지의 경로의 길이는 일정하다.
   -> 균형 트리이기 때문에.
   -> 그만큼 높이가 높아질 수록 성능 떨어진다.

2. 공간 요간

• Root 노드와 Leaf node를 제외한 각 노드는 ⌈ n/2 ⌉ ~ n 개의 자식을 가진다.
• Leaf node는 ⌈ (n-1)/2 ⌉ ~ n-1 개의 키를 가진다.

B+ Tree Node Structure

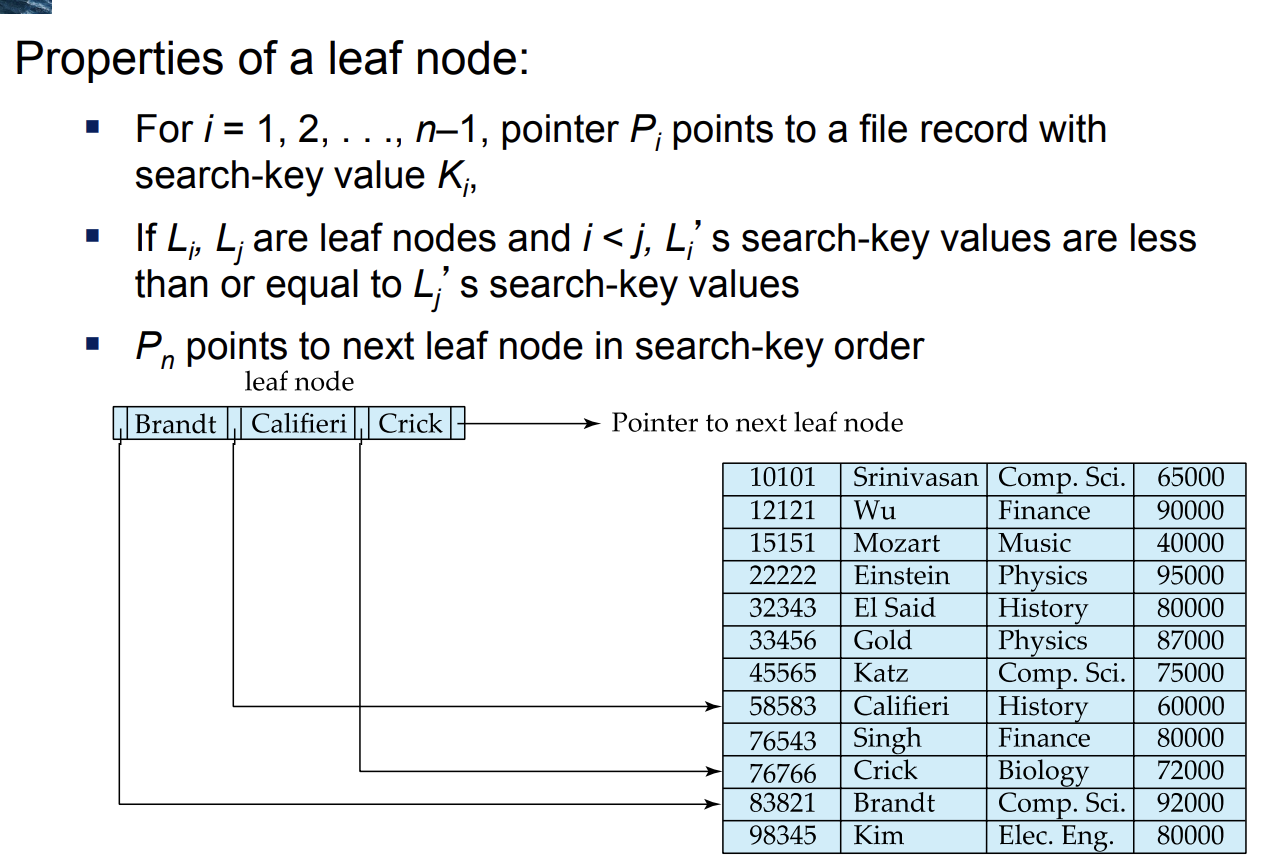
Leaf Node

leaf node인 경우에는 (Pi,Ki)가 한 쌍을 이루고 마지막 Pn은 다음 노드를 가리킨다. 각 포인터는 실제 레코드의 물리적 주소를 가리킨다.

Non Leaf Node

P1은 K1보다 작은 값을 가리킨다
나머지 Pi는 Ki-1 보다 크거나 같고 Ki보다 작은 값을 가리킨다. ( 2 <= i <= n-1)

Non-Unique Key

B+트리에서 search key가 non unique한 경우에는 다음과 같은 설계를 생각해볼 수 있다.

• leaf node의 포인터가 bucket을 가리키고 bucket에는 동일한 search key를 가진 각 레코드의 주소를 저장

• search key에 id같이 compsite key를 만들었을 때 unique해 질 수 있는 attribute와 composite key를 만들어 search key로 사용.(uniquifier) 대부분 dbms에서 사용하는 방식.

예를 들어 create index INDEX_NAME on instructor(salary) 라는 쿼리를 이용해서 교수 테이블에서 봉급을 key로 인덱스를 만들었을 때, 내부적으로는 salary가 unique하게 식별 할 수 없기 때문에 uniquifier 방식을 사용해서 salary와 id를 composite하여 search key를 만든다.

이 때 where salary = v 를 포함하는 쿼리가 들어온다면 이를 range 쿼리로 변경해 동작한다. 즉 where (salary, id) >= (80000, -inf) and (salary,id) <= (80000,+inf) 이런식으로 변경된다.

B+ Tree File 구조

지금까지 보았던 B+ Tree index는 인덱스를 저장하는 파일과 실제 레코드를 저장하는 파일이 따로 존재한다. 이와 반대로 B+ Tree File 구조는 별도의 레코드를 저장하는 파일이 없고 leaf node에 레코드를 저장한다. B+트리 파일을 사용하면 삽입, 삭제를 할 때 트리가 자동으로 업데이트 되기 때문에 인덱스와 레코드 순서가 항상 같게된다. 그렇기 때문에 clustered index를 쉽게 구현할 수 있다.

B+ Tree File에서 Secondary Index

B+ Tree File 구조에서 secondary index를 생성하면 어떻게 해야할까?

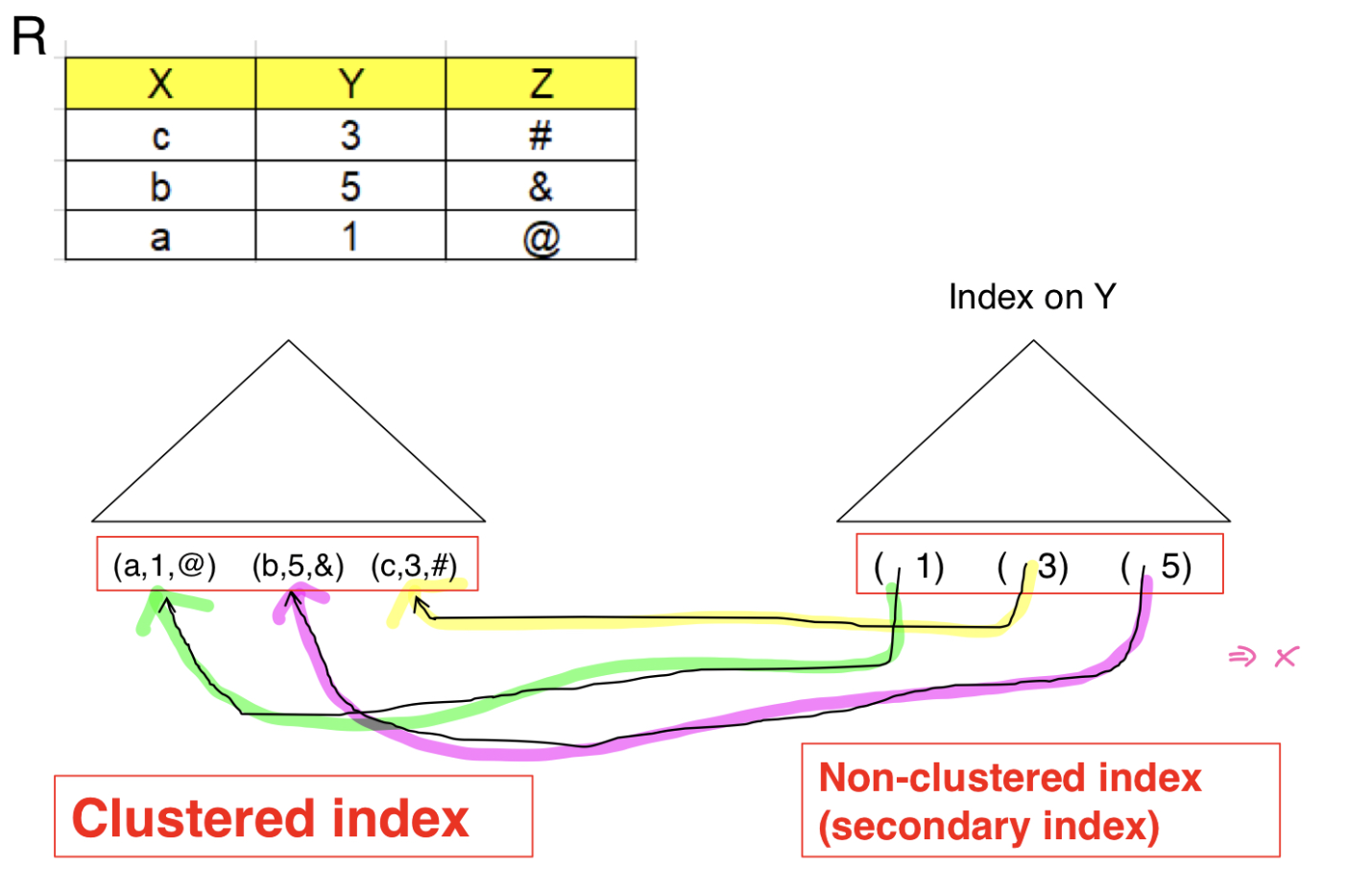
왼쪽에는 Index on X인 B+ Tree file이 있고, 오른쪽에는 Index on Y인 secondary Index가 있다. 이 때 secondary index에서 leaf node에 포인터는 B+ Tree file을 가리키도록 하면 레코드가 삽입, 삭제 될 때 B+ Tree file에서 레코드의 위치가 변경되기 때문에, 그럴때마다 secondary Index의 포인터 또한 갱신되어야 하기 때문에 오버헤드가 너무 커진다.

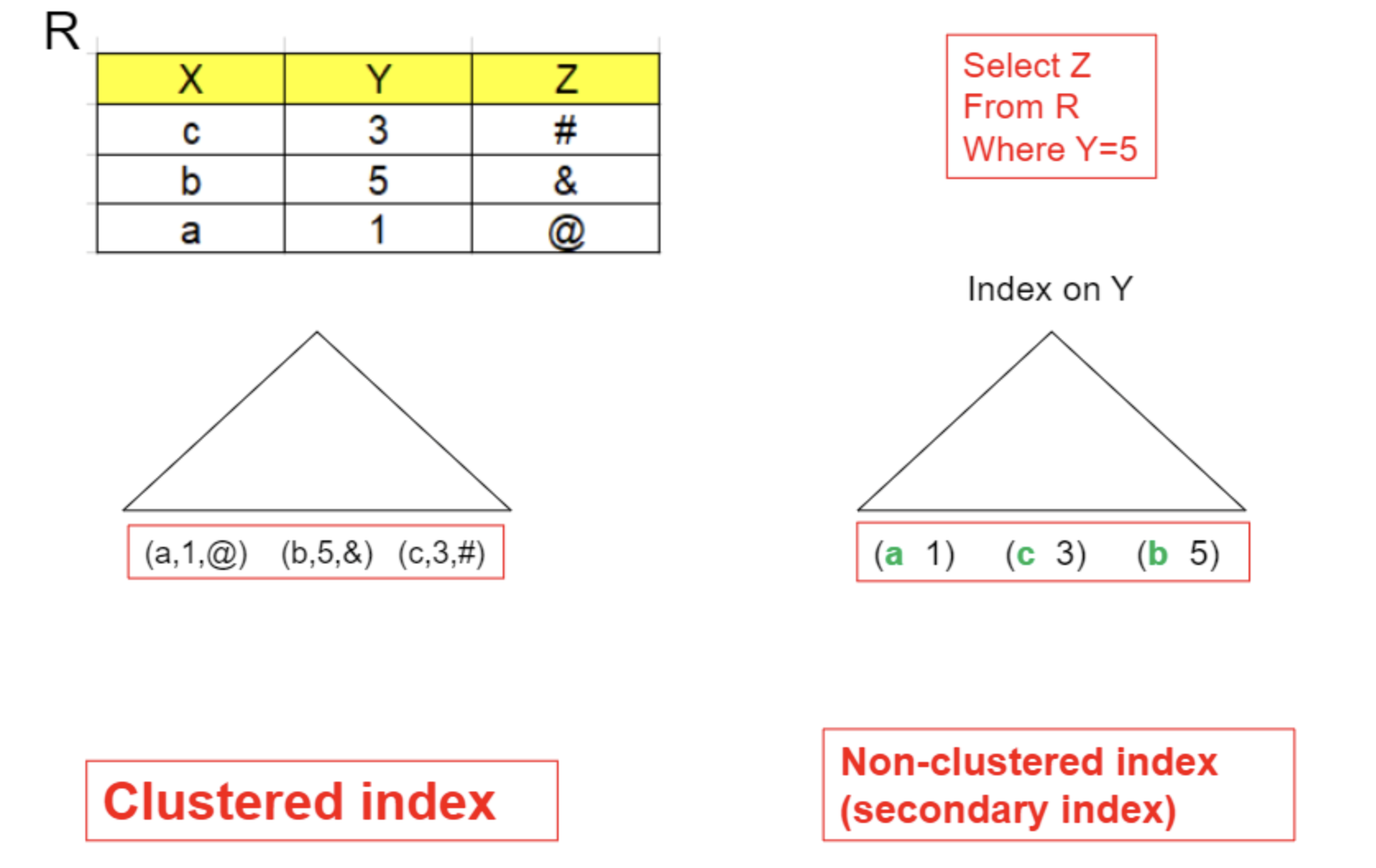
따라서 secondary index에는 clustered index의 search key를 포함하고 있다. 그렇게 되면 Y = 5 쿼리를 날리면 secondary index를 이용해서 먼저 검색을 하고 clusterd index search key로 다시 한번 B+tree index file에서 조회해서 레코드를 찾을 수 있게된다.

B Tree Index

B Tree Index는 B+ Tree Index의 원형으로 B+Tree Index와 달리 non leaf node에도 레코드로의 포인터를 가지고 있고 Key가 중복되지 않는다.

B Tree Index는 search key 중복을 최소화 하고 leaf node까지 가지 않아도 중간에 레코드를 찾을 수 있다는 장점이 있다. 하지만 leaf node에 도달하기 전에 레코드를 찾는 것이 드물고, non-leaf 노드에서 record로의 포인터를 가지고 있어야 하기 때문에 한 노드에 저장할 수 있는 키의 수가 줄어든다. 즉 트리의 높이가 높아지는 단점이 존재하고 , B+ Tree Index에 비해 삽입,삭제 연산 구현이 복잡하고 어렵다.

그리고 특히 B+ Tree Index에 비해 range query가 비효율적으로 동작한다.
B+Tree 같은 경우는 leaf node에서 next()와 같은 함수를 이용해서 쉽게 다음 레코드로 이동이 가능하지만 B Tree Index는 레코드로의 포인터가 leaf node에만 있는 것이 아니기 때문에 부모, 자식 노드를 왔다 갔다 계속해소 순회해야한다.