
주어진 쿼리를 평가는 동일한 결과를 내는 다양한 expression tree가 존재하고 각 연산에 대해 다양한 알고리즘을 적용할 수 있기 때문에 무수히 많은 경우의 수가 존재한다. 그렇기 때문에 주어진 쿼리에 대해 적절한 evaluation plan을 찾는 것이 중요하다
evaluation plan: 주어진 쿼리에 대해 어떠한 연산을 사용하고 어떻게 연산들을 조합할지와 각 연산에 대해 어떠한 알고리즘을 사용할 것인지에 대한 방법을 정의해 놓은 plan을 의미
Query Optimization
evaluation plan에 따라 cost 차이가 많이 난다. 심하면 어떤 건 seconds 어떤 건 days가 걸릴 수도 있다.
그렇기 때문에 가장 효율적인 evaluation plan을 찾아야 하는데 다양한 방식 중cost-based query optimization에 대해 알아봅시다.
cost-based query optimization
Stpes
1. equivalence rules에 따라 논리적으로 같은 결과를 만들어 내는 다양한 expressions를 생성한다.
2. 각 expressions에 대해 evaluation plans을 작성한다.
3. 가장 cheepest한 plan을 선택한다.
Estimation of plan cost based on
1. 각 relations들에 대한 통계치
2. 중간 결과에 대한 통계적인 추정
: 보통 base tabl에 대해서는 Meta data가 존재하지만 중간 결과 table들에 대한 정보는 없기 때문에 현장에서 추정해야한다.
Generate Equivalent Expressions
두 관계 대수 표현식이 존재할 때 만약 두 관계 대수 표현식이 같은 set of tuples을 만들어 내면 두 관계 대수 표현식은 equivalent하다고 할 수 있다.
(여기서 set of tuples의 순서는 상관하지 않는다.)
Equivalence Rules

E는 base table or intermediate table을 의미한다.





예제 연습
Pushing Down Selections
Pushing Down Selections : select을 가능한 빨리 할 수록 join할 때 relation의 size를 줄일 수 있다.
Q. 'Music' 학부에 있는 모든 강사의 이름과 해당 강사가 가르치는 과정의 제목을 찾아라.
instructor realtion에서 먼저 dept_name = 'Music'인 tuple을 select하고 join을 함. 이렇게 하면 join에 참여하는 relatin의 size를 줄일 수 있음.

Pushing Down Projections
Pushing Down Projections : project을 가능한 빨리 할 수록 join할 relation의 size를 줄일 수 있다.
다음과 같은 표현식이 있을 때 σ(dept_name = “Music” (instructor ⨝ teaches)
를 수행하면 (ID, name, dept_name, salary, course_id, sec_id, semester, year) attributes을 포함하는 중간 결과를 얻을 수 있다.
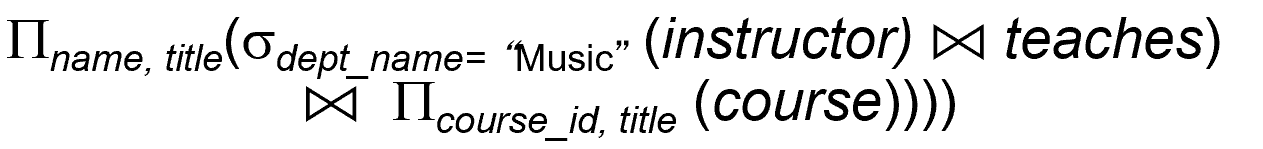
이를 8a, 8b 규칙을 적용하면 다음과 같이 만들 수 있다. 이렇게 하면 immediate table을 생성할 때 불필요한 attributes 없앨 수 있어 join 되는 relation의 size를 줄일 수 있다.

Join Ordering
조인 결합법칙에 따라
(r1 ⨝ r2) ⨝ r3 = r1 ⨝ (r2 ⨝ r3) 성립한다.
이때 (r2 ⨝ r3)의 결과의 size가 크고 (r1 ⨝ r2)의 결과의 size가 작으면
(r1 ⨝ r2) ⨝ r3 순서로 Join을 진행한다. 그렇게 하면 더 작은 크기의 임시 relation을 가지고 연산할 수 있다.
Cost Estimation

Selection Size Estimation
- σA=v(r)
- 정규 분포인 경우 ,
Nr / V(A,r) - A가 key attribute 인 경우, 1
- σA<=v(r)
Nr * (v - min(A,r)) / (max(A,r) - min(A,r))- 만약 정보를 얻을 수 없으면 Nr / 2 로 가정
Complex Selections Size Estimation
selectivity of a conditoin θi : θi를 충족할 확률
만약 θi를 만족하는 튜플이 100개이고 , Nr이 200 이면 selectivity = 1/2
- Conjunction : σθ1 ^ θ2 ^ ... ^ θn(r)
Nr * (S1 * S2 * ... * Sn) / (Nr^n)
- Disjunction : σθ1 v θ2 v ... v θn(r)
Nr*(1-(1-S1/Nr)*(1-S2/Nr)*...*(1-Sn/Nr))
- Negation
nr - size(σθ(r))
Joins Size Estimation
R , S : r,s의 set of attriutes
- R ∩ S = ø
r ⨝ s = r x s
- R ∩ S = a key of r
- r의 key가 교집합인 경우, s는 최대 r에 있는 1개의 tuple과 짝을 이룰 것.
따라서,r ⨝ s 의 수는 = s의 tuple수보다 작거나 같다
- R ∩ S = a foreign key of r
- 외래키 무결성 조약에 의해 s의 외래키는 r에 무조건 존재,
r ⨝ s 의 수는 = s의 tuple수와 같다
- R ∩ S = {A} not a key for R or S
-Nr * (Ns / V(A,s)) , Ns * (Nr / V(A,r))둘 중 더 작은 값으로 추정
