데이터 베이스 시스템에서 조인 연산을 구현하는 다양한 알고리즘이 존재합니다. 대표적으로 Nested Loop Join , Sort Merge Join ,Hash join이 존재합니다.

---

앞으로 사용할 Student와 Takes 테이블 관련 정보는 다음과 같습니다.
(Student : r , Takes : s )

• number of records of Student : 5,000
• number of blocks of Student : 100
• blocking factor of Student : 50
• number of records of Takes : 10,000
• number of blocks of Takes : 400
• blocking factor of Takes : 25
• M : 사용가능한 버퍼의 수

Nested Loop Join

• 모든 조인 조건에 대해 적용가능함.

r : Student 테이블, s : Takes 테이블
N : record 수, B : 블록 수

Nested-Loop Join

Nested Loop Join은 가장 간단한 조인 알고리즘 중 하나입니다. 대략적으로 이 알고리즘은 두 개의 테이블을 중첩된 루프로 순회하면서 일치하는 행을 찾습니다. 즉, 외부 루프는 첫 번째 테이블의 모든 행을 순회하고, 내부 루프는 두 번째 테이블의 모든 행을 순회하면서 일치하는 행을 찾습니다.

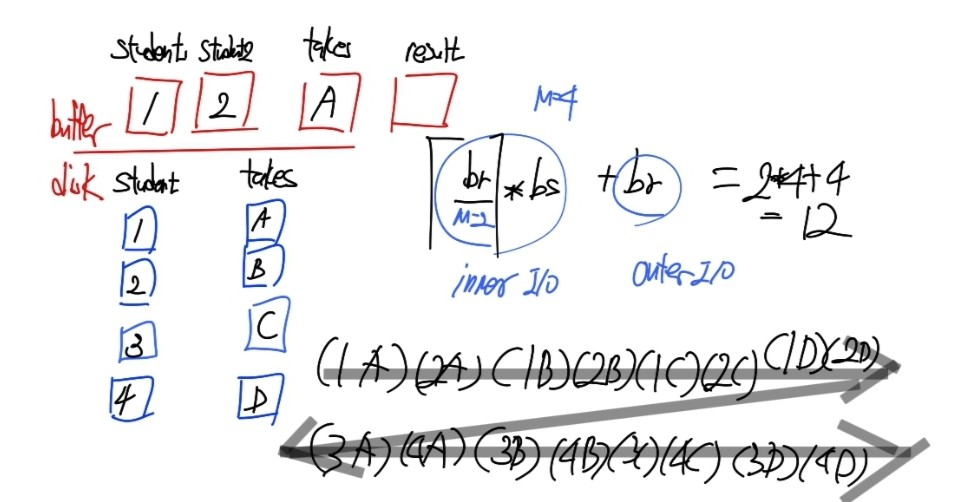
• M = 3 , Nr * Bs + Br 만큼의 IO 연산 발생
  사용가능한 버퍼의 수가 3개 일 때는 1개는 외부 루프용, 1개는 내부 루프용, 1개는 결과 저장용으로 사용하게 된다.
  Student의 첫 번째 레코드와 Takes의 첫 번째 블록에 있는 모든 레코드와 비교를 진행한다. 그리고 Takes의 두 번째 블록을 버퍼로 불러와 다시 Student의 첫 번째 레코드와 비교한다. 그렇게 Takes의 400번째 블록과 비교를 진행하고, Student의 두 번째 레코드 처음부터 다시 비교를 진행한다.

• M >= min(Br,Bs) + 2 , Bs + Br 만큼의 IO 연산 발생
  Br, Bs 중 개수가 더 작은 것을 메모리에 모두 올려 놓고, 이를 내부 루프로 사용하면 반복해서 내부 블록을 IO 연산할 필요 없게 된다.
  Student의 블록의 수가 더 작기 때문에 이때는 Student가 내부 루프에서 돌고, Takes가 외부 루프에서 돈다. Student의 모든 블록을 버퍼로 불러오고, Takes는 첫 번째 블록만 버퍼로 불러온다. 이 때는 Student의 모든 블록이 모두 메모리에 올라와 있기 때문에 M = 3인 상황처럼 내부 루프에 있는 블록을 버퍼에 올렸다 내렸다 할 필요가 없다.

Block nested-loop join

Block nested-loop join에서는 outer table에서 block 단위로 비교를 진행한다.

• M = 3 , Br*Bs + Br 만큼의 IO 연산 발생

Student의 첫 번째 블록을 버퍼로 올린다. 마찬가지로 Takes의 첫 번째 블록을 버퍼로 올린다. 이 때 비교를 Student 첫 번째 블록에 있는 모든 레코드와 비교한다.
(S1,T1), (S1,T2), ... , (S1,T25),
(S2,T1), (S2,T2), ... , (S2,T25),
(S50,T1), (S50,T2), ... , (S50,T25),
다 비교하면 Takes의 두 번째 블록을 올리고 다시 Student의 첫 번째 블록에 있는 모든 레코드와 비교한다.

• M >= min(Br,Bs) + 2 , Bs + Br 만큼의 IO 연산 발생

• IO 연산 횟수를 일반화하면 ⌈Br/(M-2)⌉ * Bs + Br
  

Indexed Nested-Loop join

이 방식은 File을 scan 하는 방식 대신에 Index를 scan하는 방식이다.
inner table의 join attribute로 Index가 존재할 때 사용가능하다.

• IO 연산 횟수는 Br + Nr * C
  ( C 는 B+ 트리 Index라면 높이 + alpha )

• 만약 집중 인덱스라고 한다면 100 + 5000 * 5 = 25,100 IO 발생.
  한 노드에 20 entries가 있다면, B+ tree index의 높이는 4이다. 그리고 집중이기 때문에 해당 레코드가 한 블록에 모여 있을 것이라고 가정하면 플러스 한번만 더 IO 해서 해당 블록으로 찾아가면 된다. 따라서 C = 4 + 1 = 5

• 만약 비집중 인덱스라고 한다면, C = 4 + 2 . 그 이유는 Nr = 5000, Ns = 10000이기 때문에 한 학생당 2개의 과목을 수강 중일 것이다. 따라서 인덱스 높이만큼 IO한 후 각 takes가 다른 블록에 있을 것이기 때문에 각 각 IO해줘야함.

Sort Merge Join

Sort Merge Join은 두 개의 테이블에서 조인 조건에 해당하는 열을 기준으로 각각 정렬한 다음, 정렬된 데이터를 병합하면서 일치하는 행을 찾습니다.
equi 조인에 대해서만 적용할 수 있다.

• M =3 , Br + Bs 만큼의 IO 연산 발생
  ( m = 3 이면 1 path join은 아닐 수 있지만 rough하게 1 path만에 join 가능하다고 가정)
• 정렬이 안 되어 있으면 IO 연산은 추가 될 수 있음 ( 정렬 후 OUTPUT을 디스크에 쓰는 연산도 추가되어야함.)

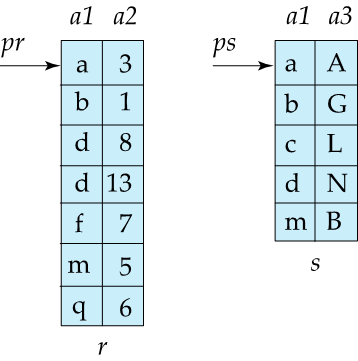
a1이 join attribute 이고 r,s 모두 a1에 대해 정렬된 상태. pr, ps 는 각 레코드를 가리키는 포인터.

Hash Join

Hash Join은 두 개의 테이블을 해시 함수를 사용하여 두 개의 해시 테이블로 변환한 다음, 해시 테이블 간에 조인을 수행하는 방식으로 동작합니다. 먼저, 조인 조건에 해당하는 열을 기준으로 두 개의 테이블을 해시 함수를 사용하여 각 파티션에 저장합니다.

r에 속한 튜플 tr 에서 join attribute를 hash 함수에 넣어서 얻은 결과 i였을 때 tr 을 파티션 ri에 저장. s도 마찬가지.

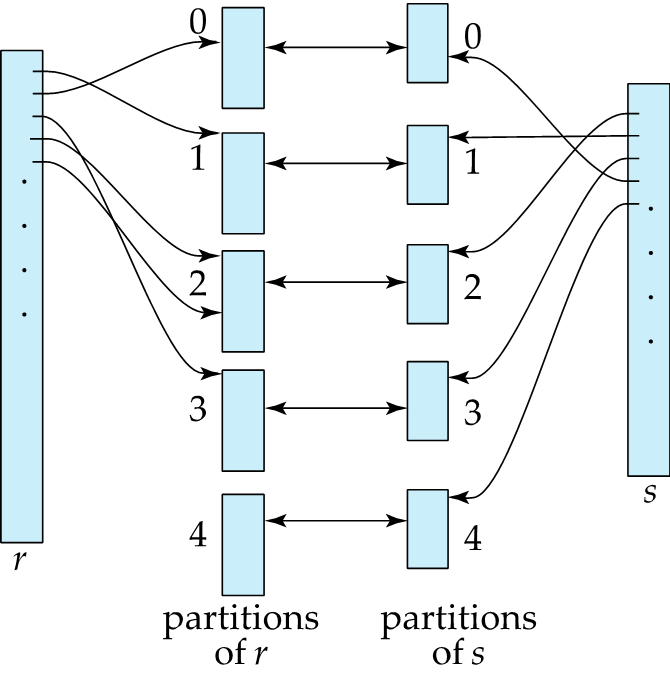
Br은 100, Bs 400 일 때 균등하게 hash function이 작동했다고 하면 r의 각 파티션들은 100 / 5 = 20 block이 있을 것이고, s의 각 파티션들은 400 / 5 = 80 block이 포함되어 있을 것.

join할 때는 r의 i 번째 파티션에 포함되어 있는 모든 블록을 메모리로 올린다. 그리고 s의 i번재 파티션에 포함되어 있는 한 개의 블록을 올리고, 조인 조건을 비교한다. 그렇게 되면 M = 20 + 1 + 1(output) = 22 만큼 필요.

• M = 22 , 3(Br+Bs) 만큼의 IO 필요.
  1 : 파티션 만들 때 각 블록을 메모리에 올리고
  1 : 파티션을 저장할 때
  1 : 조인할 때
  -> 따라서 (1+1+1) = 3 * (Br+Bs)

• 파티션을 만들 때 필요한 M = the number of partitions + 1 = 5 + 1 = 6

구체적인 과정은 다음과 같다.

여기서 중요한건 join할 때 in-memory hash index를 만든 다는 것. 즉 build input의 한 파티션을 메모리에 올리고, 올라온 tuple들을 가지고 hash index를 만드는데, 여기서 사용하는 해쉬 함수는 파티션을 만들 때 사용한 해쉬 함수와는 다른 것! in-memory hash index를 만들면 probe input의 tr과 매칭이 되는 짝인 ts를 인덱스를 이용해 더 빠르게 찾을 수 있음.

build input은 각 파티션에 포함된 블록이 더 적은 relation으로 정한다. 여기선 Student가 20 blocks per partition 이고 , Takes가 80 blocks per partition이기 때문에 Student가 build input.