그리디 알고리즘은 가장 유명하고 기초적이지만 제가 생각하기에는 가장 어려운 유형의 알고리즘입니다.
그리디 알고리즘은 말 그대로 매 선택에서 눈앞의 가장 큰 이익만을 좇는 방법입니다.
그리디 알고리즘이 적용되기 위해서는 2가지 성질을 만족해야합니다.
- 탐욕 선택 속성(Greedy Choice Property) : locally optimal choice lead to a globally optimal solution.
- 최적 부분 구조(Optimal Substructure) : the optimal solution to a problem incorporates the optimal solution to subproblems.
1번은 현재 최적이라고 선택한 것이 이후의 선택에 영향을 주지 않고 번복될 일이 없어야 함을 의미합니다. (딱, 현재 처한 문제 상황에서 최적이라고 생각한 선택이 번복될 일이 없고, 이후 선택에도 영향을 끼치지 않음.)
2번은 큰 문제의 최적해에 작은 부분 문제의 최적해가 포함된다는 의미입니다. (재귀적으로 생각,그렇다고 재귀로 풀라는 건 아님, 큰 문제에서 최적해 구하고 -> 다음 부분 문제에서 최적해 구하고 -> 또 부분 문제에서 최적해 구하고 -> ... ;; 과거에 문제가 미래에 문제에 영향을 주지 않음) 즉 같은 전략을 반복적으로 취하며 문제의 최적해를 구할 수 있다는 것입니다.
1번과 2번을 종합해보면 코테에서 그리디 알고리즘을 적용할 수 있는 경우는 내가 부분 문제에서 적용한 눈 앞에 가장 큰 이득을 얻을 수 있도록 취한 전략이 반복적으로 적용 되어야 하며(이후에 선택에 영향을 주지 않음), 이 방식을 통해 최적해를 구할 수 있어야 합니다.
cf) 동적계획법도 마찬가지로 2번의 성질을 갖지만 이외의 다른 성질을 갖습니다. 동적계획법 같은 경우에는 문제가 Overlapping 되기 때문에 이전의 작은 문제의 결과가 다음에 풀 문제에 영향을 끼치게 됩니다.
( 밑에 예시는 출처1에서 가지고 왔습니다.)
동전 교환하기
10원짜리, 50원짜리, 100원짜리, 500원짜리 동전들을 사용해서 어떤 금액을 표현하려 합니다.
이때 각 동전은 무수히 많은 대신, 동전 개수를 최소로 사용해야 한다면 어떻게 할까요?
무조건 사용할 수 있는 한 가장 큰 금액의 동전을 많이 사용하는 겁니다.
예를 들어보죠. 620원이 있다면, 620원 이하의 가장 큰 액수가 500원짜리이므로
먼저 500원짜리 동전을 하나 사용하고, 120원이 남습니다.
이제 500원짜리는 못 쓰죠. 대신 그 다음으로 큰 100원짜리를 사용할 수 있습니다.
그리고 남은 20원은 10원짜리 2개를 사용할 수밖에 없고 이렇게 하면 답은 동전 4개가 됩니다.
880원의 경우는 마찬가지로 500+100+100+100+50+10+10+10으로 나타낼 수 있고 답은 8.
이게 성립하는 이유는 반드시 큰 쪽의 동전은 작은 쪽 액수의 배수라는 겁니다.
만약 저 배수의 성질이 깨진다면 그리디 알고리즘을 사용할 수 없겠죠.(이 때는 동적계획법을 이용)
도시락 데우기
N개의 도시락이 있고, 전자레인지는 단 한 대만 존재하며 한 번에 하나의 도시락만 데울 수 있고,
각 도시락은 조리시간과 먹는 시간이 다르게 정해져 있습니다.
이때, 도시락을 적절한 순서로 조리하면 첫 번째 도시락을 데우기 시작한 순간으로부터 모든 도시락을 다 먹는 데 걸리는 시간이 최소가 되게 할 수 있습니다(다 데운 도시락은 바로 누군가가 먹는다고 합시다).
이 시간을 최소화하려면 무조건 먹는 데 시간이 오래 걸리는 도시락부터 순서대로 데우면 됩니다.
왜냐면, 도시락을 데우고 나서 바로 다른 도시락을 데우는 걸 반복하고, 각 도시락을 데우는 시간은 정해져 있으므로 우리는 도시락을 데우는 시간을 줄이는 건 불가능합니다.
그러나 만약 마지막으로 데운 도시락을 먹는 데 오랜 시간이 걸린다면 전체 시간도 길어지는 것이 자명하죠. 따라서 먹는 데 오래 걸리는 것을 먼저 데우고 먼저 먹기 시작하게 하는 겁니다.
이게 과연 항상 성립할까요?
두 도시락 1, 2가 있고 각각 데우는 시간이 C1, C2, 먹는 시간이 E1, E2라고 합시다. 또한 E1 >= E2라고 합시다.이제 1번을 먼저 데우는 것이 반드시 2번을 먼저 데우는 것 이상의 효과를 낸다는 것을 증명하면 됩니다. 1번과 2번은 연속적으로 데운다고 가정합니다.
2번을 먼저 데운다고 가정한다면 총 걸린 시간은 C2 + C1 + MAX(E1,E2-C1)입니다. 하지만 이 때 E1 >= E2 이기 때문에 항상 E1이 E2-C1보다 크게 됩니다. 즉 총 걸린 시간은 C2+C1+E1입니다.
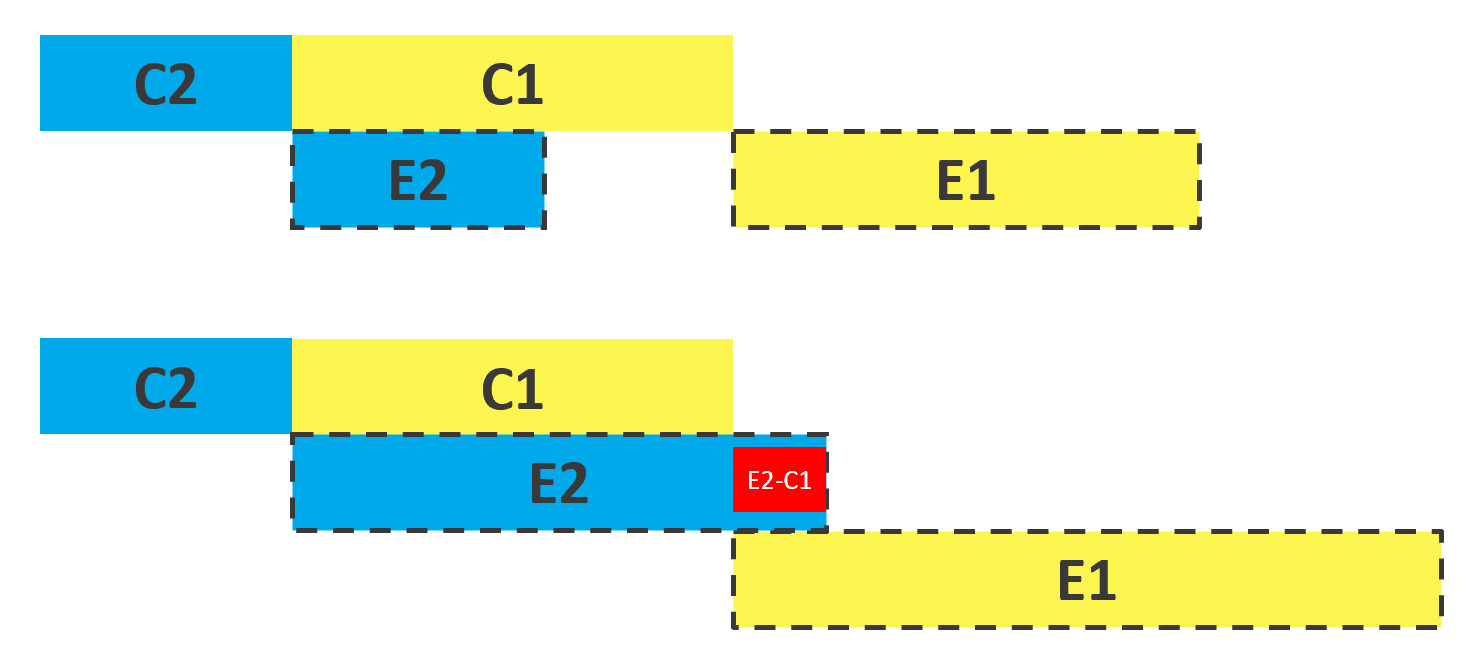
다음으로 1번을 먼저 데운다고 가정하면 총 걸린 시간은 C1 + C2 + MAX(E1-C2, E2)입니다.
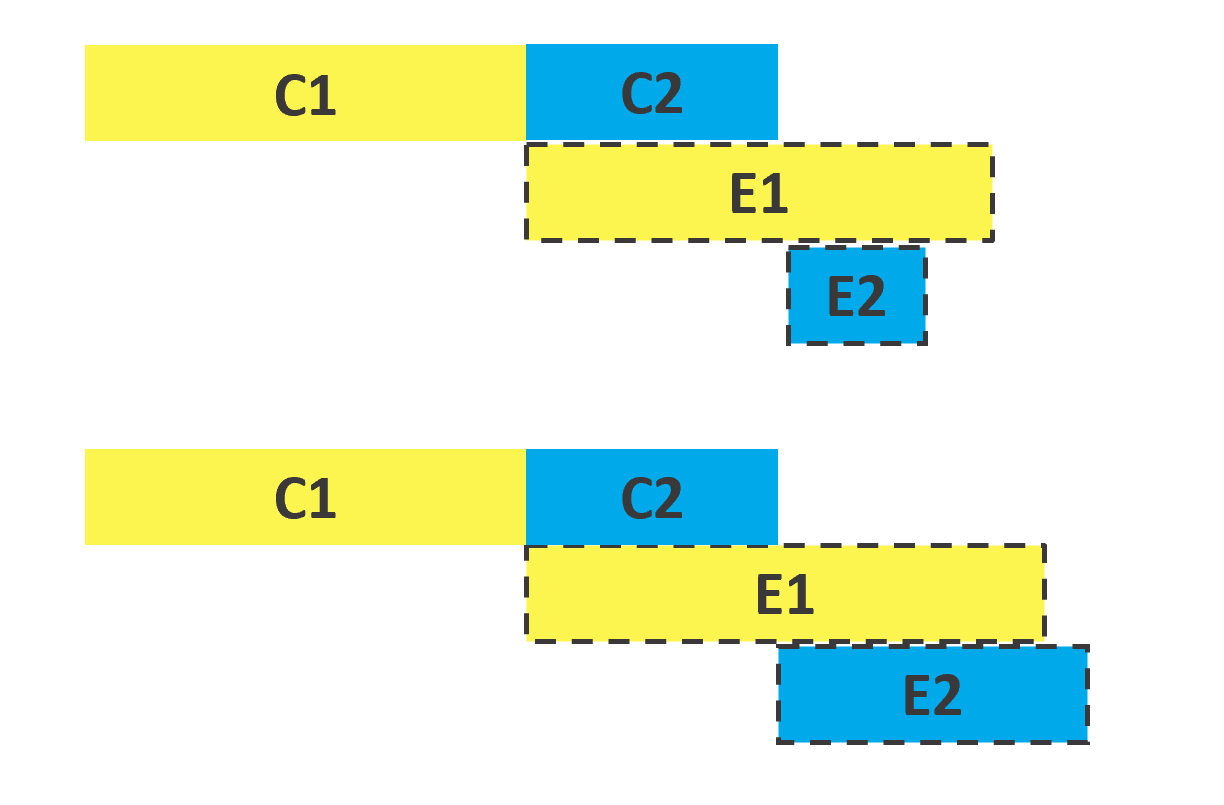
이 때 C1+C2 == C2+C1이기 때문에 , E1 과 MAX(E1-C2,E2)를 비교해서 후자가 더 작으면 증명이 완료됩니다.
먼저 E1 >= E1 - C2 는 자명합니다. ( C2 >=0 ) , 그리고 E1 >= E2 또한 참입니다.(문제 조건) 따라서 먹는 시간이 더 긴 E1을 먼저 데우는 것이 반드시 전체 시간이 줄어든다라는 것을 알 수 있습니다. 이를 일반화하여 N개의 경우에도 증명이 가능합니다.
즉, 이 두 문제에서 모두 그리디 알고리즘의 속성을 만족합니다.
문제의 성질이 동일하게 보존되고, 같은 전략을 반복적으로 취할 수 있는 것이 그리디 알고리즘의 특징입니다.
동전 문제의 경우 1번 속성을 만족함을 각 동전이 약수이기 때문에 증명이 가능하고 2번 속성 또한 가장 큰 동전을 한 번 사용하면 남은 금액을 다시 최소 개수의 동전을 사용하여 나타내는 부분 문제가 된다. 따라서 2번 속성 또한 만족한다.
도시락 문제의 경우 또한 1번 속성을 만족함을 증명했고, 도시락 하나를 데운 후 그 다음에 다시 남은 도시락 중 제일 먹는 시간이 오래 걸리는 것을 선택하는 전략을 고수합니다.
(보통 2번 속성은 1번이 증명되면 거의 자명함)
그렇지만 그리디 알고리즘이 제대로 동작하지 않는 경우도 많습니다.
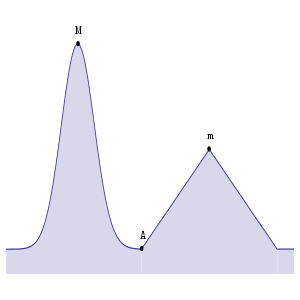
내가 만약 A지점에 있다고 할 때 좌우로 적절히 이동하여 최대 높이에 다다르려고 합니다. 높이가 높을수록 이득! 이 때 m은 local maximum(근처 지역에서는 최대이지만 , 전체 중에서 최적해는 아님) 이고 M은 global maximum(local maximum이기도 하면서 전체에서 최적해를 의미)입니다.
그러나 전체 상황을 알 수 없는 현재 상황(A)에서는 어딘가 도착해도 이게 global한 최적해인지 local한 최적해인지 알 수 없습니다.
여기서 그리디 알고리즘을 적용해봅시다. 나의 전략은 "현재 상황에서 경사가 더 높은 부분을 올라가는 거야" 라고 해봅시다.
그러면 A에서 경사가 더 높은 오른쪽을 선택하게 될 겁니다. 이 전략을 반복적으로 적용해서 결국에는 m에 도달하게 될겁니다.
결국 이 그리디 전략은 1번 속성을 만족하지 못합니다. 현재 최적이라고 생각한 선택이 사실은 최적이 아니였고 번복해야 하기 때문입니다. (A지점에서 처음 내가 선택한 전략부터 번복해야함,,) 즉 1번 속성의 영어로 적은 것도 여기서 이해할 수 있습니다. 눈앞에 택한 전략이 globally optimal solution으로 lead to 하지 못 한 겁니다.
한번 2번 속성 또한 이 전략은 애초에 문제의 크기가 작더라도 global한 최적해가 subproblem의 최적해를 포함하고 있지 않습니다. (global한 최적해는 왼쪽으로 가는 건데, 이 전략은 다 오른쪽으로 가버리니까..)
즉 이 문제에서 그리디한 알고리즘을 적용해서 풀 수 없는 문제이고 다른 방법을 찾아봐야 겠죠. (완전 탐색같은)
