
개요
오늘 알아볼 것은 그 유명한 동적계획법입니다. DP라고도 많이 합니다. 여기서 '다이나믹'은 이 기법이랑은 아무런 상관이 없습니다.. 그냥 만든 사람이 뭔가,, 멋있어 보여서 붙여다고..
아무튼 코딩테스트나 알고리즘 대회에서 거의 밥먹듯이 출제되고 기본 소양으로 취급되는 분야입니다. 하지만 그만큼 입문하기도 쉬운만큼 정복하기도 어렵습니다. 그럼 이제 동적계획법이 뭔지 한번 알아보겠습니다.
DP를 사용하는 이유
일반적인 재귀 방식 또한 DP와 매우 유사하디. 가장 큰 차이점은 일반적인 재귀를 단순히 사용 할 때 동일한 작은 문제들이 여러 번 반복되어 비효율적인 계산이 될 수 있다는 것입니다.
그 예시로 가장 많이 나오는 것이 피보나치 수열입니다.
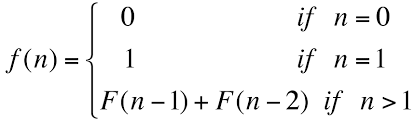
위 점화식을 재귀함수로 작성하면 다음과 같이 작성할 수 있습니다. 그리고 각 함수가 몇 번 호출 되었는지 알아보기 위해 count배열을 만들었습니다.
N = 10일 때 그 수를 구해보면 다음과 같습니다.
public class Fibonacci{
public static int[] count = new int[100];
public static void main(String args[]) {
int n = 10;
System.out.println(fibonacci(n));
int i = 0;
for (int c : count) {
if(i > n ) break;
System.out.println("F("+i+++")"+"메소드 실행횟수:" + c);
}
}
public static int fibonacci(int n) {
count[n]++;
if (n < 2) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
} 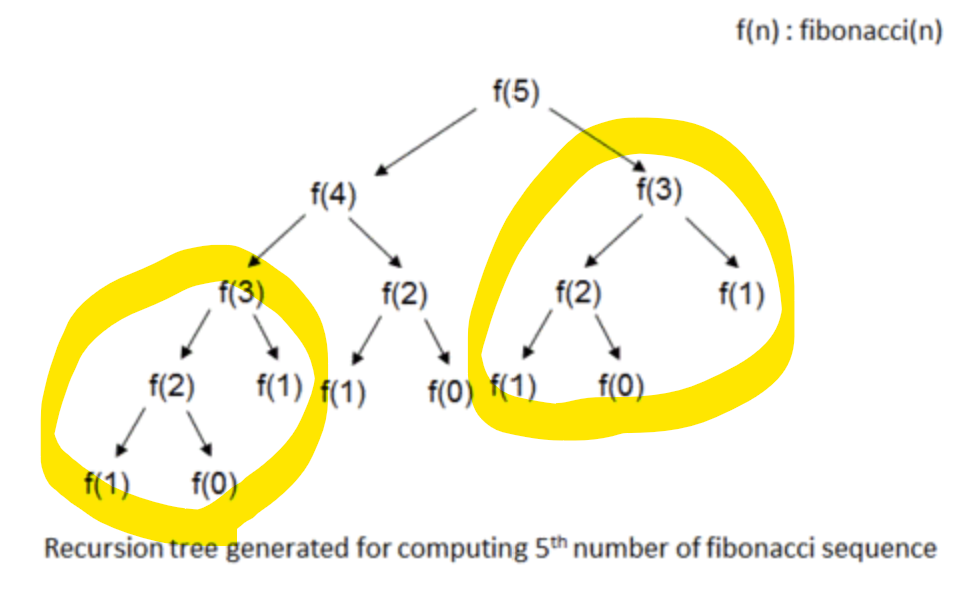
그 이유는 프로그램이 실행되는 상황을 보면 알 수 있습니다. F(5)를 구할 구하기 위해 F(4)와 F(3)을 알아야 합니다. 그런데 F(4)를 구하기 위해서는 F(3)과 F(2)를 알아야 하기 때문에 , F(4)를 계산했을 시점에는 이미 F(3)을 알고 있습니다. 그럼에도 불구하고 다시 F(3)을 계산하는 뻘짓거리를 하게됩니다. 이런식으로 다른 케이스들도 같은 상황이 발생합니다. 이렇게 되면 기하급수적으로 호출 횟수가 증가하기 때문에 시간복잡도가 지수 시간이 걸리게 됩니다.
여기서 한 번 구한 값을 저장해두고 재사용 한다면 어떻게 될까요? 이렇게 되면 다항 시간안에 계산이 가능해집니다. 즉 매우 효율적으로 문제를 해결할 수 있게 됩니다.
DP 정의
DP는 다음과 같이 정의합니다.
주어진 문제를 여러 개의 부분 문제들로 나누어 푼 다음, 그 결과들로 주어진 문제를 푼다
그런데 이 정의는 분할정복도 비슷했던 것 같은데.. 그렇지만 이 둘사이에는 큰 차이가 있습니다.
가장 먼저 분할 정복은 문제를 분할했을 때 겹치는 문제가 발생하지 않지만
DP는 겹치는 문제가 발생하기 떄문에 메모이제이션 같은 기법이 필요합니다.
그리고 문제의 크기가 줄어드는 속도가 분할정복이 지수 속도로 줄어들지만 DP는 다항식 혹은 상수 속도로 줄어듭니다. 이게 무슨 말이냐면 보통 분할정복은 문제의 크기가 1/2 , 1/4 , 1/8 이런 식으로 줄어들지만 DP는 피보나치만 봐도 N , N-1, N-2 , N-3 ... 이런식으로 줄어듭니다.
또한 DP같은 경우 메모리까지 소비해가며 샅샅이 뒤진다는점에서 실행시간이 그리디 알고리즘에 비해 떨어지지만, 그리디 알고리즘보다 좀 더 근사치가 아닌 정확한 값을 얻을 수 있습니다.
DP 사용 조건
정리하면 DP는 다음과 같은 문제 상황에서 사용합니다.
- 겹치는 부분 문제 (Overlapping Subproblems)
- 최적 부분 구조(Optimal SubStructure)
겹치는 부분 문제 (Overlapping Subproblems)
DP는 기본적으로 문제를 나누고 그 문제의 결과값을 이용하여 전체 답을 구합니다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능합니다.
그렇기 때문에 부분 문제의 결과값을 저장하여 다음번에 사용할 때 재계산 하지 않도록 합니다.
최적 부분 구조(Optimal SubStructure)
부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과 값을 나타낼 수 있는 경우를 의미합니다. 즉, 전체 문제의 최적해가 부분 문제의 최적해들로써 구성된다는 것을 의미합니다.
예를 들어, A라는 문제의 부분 문제 a,b가 있을 때, a,b의 최적해는 a',b'라고 가정한다면 A의 최적해는 a'와 b'로써 구성됩니다. 다시 말해, A라는 문제가 최적 부분 구조를 가지고 있는데 방금과 같은 조건에서 A의 최적해는 a'와 b'로 구성되는 것을 증명한다면, 최적 부분 구조를 가진다는 것을 언급하며 이로 인해 A의 최적해가 a'와 b'가 아닌 a'와 c'으로 구성된다고 가정한다면 b의 최적해는 c'이어야 하는데 b의 최적해는 b'이기 때문에 가정이 모순임을 보여 증명할 수 있습니다.
이때 문제가 최적 부분 구조를 가지고 있지 않음에도 최적 부분구조를 가지고 있다고 가정하지 않도록 주의해야 합니다.
예를 들어,
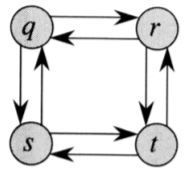
두 정점 A,B에 대해서 최단 경로와 최장 경로를 다음과 같이 정의할 때,
최단 경로: A-B까지 연결되는 가장 적은 개수의 간선들로 이루어 지는 경로
최장 경로: A-B까지 연결되는 가장 많은 개수의 간선들로 이루어 지는 경로
최단 경로
위 그림에서 q - t사이의 최단 경로는 무엇일까요?
q - r - t or q - s - t 입니다.
각 각을 부분 문제로 나누어 보았을 때 최적해는 어떻게 될까요?
q 와 r 사이의 최단경로는 q - r 이며, r과 t사이의 최단경로는 r - t 입니다.
이러한 것을 보아 최적 부분 구조를 가지고 있다고 알 수 있습니다.
최장 경로
그렇다면 q - t 사이의 최장 경로는 어떻게 될까요?
최장 경로 또한 q - r - t ( q - s - t 도 가능) 입니다.
각 각을 부분 문제로 나누었을 때 최장 경로는 어떻게 되나요? q - r 사이의 최장경로는
q - r 이 아닌 q - s - t - r 이 됩니다.
이 예시는 최장 경로를 찾는 문제가 최적 부분 구조를 가지지 않을 뿐만 아니라 부분 문제들의 최적해로부터 전체 문제의 조건에 맞는 해를 언제나 만들어 낼 수 있는 것은 아니라는 사실을 보여줍니다.
DP 사용하기
DP를 적용할 수 있는 문제는 꽤 다양하고 기초부터 응용까지 문제 난이도가 천차만별입니다. 일반적으로 DP를 사용하기 앞서서 아래의 과정을 거쳐 진행합니다.
1. DP로 풀 수 있는 문제인지 확인하기
2. 문제의 변수 파악
3. 변수간 관계식 만들기
4. 메모하기(Memorizaiotn, Tabulation)
5. 기저 상태 파악하기
6. 구현하기
1. DP로 풀 수 있는 문제인지 확인하기
사실 이 1번 부분이 가장 어렵습니다. 우선 DP 사용 조건에서 봤듯이, 현재 문제가 작은 부분 문제의 해로 구성되는 가를 파악해야 합니다. 그 이후, 큰 문제와 작은 문제들관의 관계를 파악할 수 있어야 합니다.
2. 문제의 변수 파악
DP는 현재 변수에 따라 그 결과 값을 찾고 그것을 전달하여 재사용하는 것을 거칩니다. 즉, 문제 내 변수의 개수를 알아내야 한다는 것. 이것을 영어로 "state"를 결정한다고 한다.
예를 들어, 피보나치 수열에서는 n번째 숫자를 구하는 것이므로 n이 변수가 된다. 그 변수가 얼마이냐에 따라 결과값이 다르지만 그 결과를 재사용하고 있다.
또한, 문자열 간의 차이를 구할 때는 문자열의 길이, Edit 거리 등 2가지 변수를 사용한다. 해당 문제를 몰라도 된다.
또, 유명한 Knapsack 문제에서는 index, 무게로 2가지의 변수를 사용한다. 이와 같이 해당 문제에서 어떤 변수가 있는지를 파악해야 그에 따른 답을 구할 수 있다.
3. 변수 간 관계식 만들기
변수들에 의해 결과 값이 달라지지만 동일한 변수값인 경우 결과는 동일하다. 또한 우리는 그 결과값을 그대로 이용할 것이므로 그 관계식을 만들어낼 수 있어야 한다.
그러한 식을 점화식이라고 부르며 그를 통해 우리면 짧은 코드 내에서 반복/재귀를 통해 문제가 자동으로 해결되도록 구축할 수 있게 된다.
예를 들어 피보나치 수열에서는 f(n) = f(n-1) + f(n-2) 였다. 이는 변수의 개수, 문제의 상황마다 모두 다를 수 있다.
4. 메모하기
변수 간 관계식까지 정상적으로 생성되었다면 변수의 값에 따른 결과를 저장해야 한다. 이것을 메모한다고 하여 Memoization이라고 부른다.
변수 값에 따른 결과를 저장할 배열 등을 미리 만들고 그 결과를 나올 때마다 배열 내에 저장하고 그 저장된 값을 재사용하는 방식으로 문제를 해결해 나간다.
이 결과 값을 저장할 때는 보통 배열을 쓰며 변수의 개수에 따라 배열의 차원이 1~3차원 등 다양할 수 있다
5. 기저 상태 파악하기
여기까지 진행했으면, 가장 작은 문제의 상태를 알아야 한다. 보통 몇 가지 예시를 직접 손으로 테스트하여 구성하는 경우가 많다.
피보나치 수열을 예시로 들면, f(0) = 0, f(1) = 1과 같은 방식이다. 이후 두 가지 숫자를 더해가며 값을 구하지만 가장 작은 문제는 저 2개로 볼 수 있다.
해당 기저 문제에 대해 파악 후 미리 배열 등에 저장해두면 된다. 이 경우, 피보나치 수열은 매우 간단했지만 문제에 따라 좀 복잡할 수 있다.
6. 구현하기
DP는 2가지 방식으로 구현할 수 있다.
1) Bottom-Up (Tabulation 방식) - 반복문 사용
2) Top-Down (Memoization 방식) - 재귀 사용
백준 1463번 1로 만들기
이 문제의 경우 N을 1로 만드는 최소 횟수를 f(N)이라고 하면
f(N) = min(f(N-1) + 1,
f(N/3) - 1 (N이 3의 배수인 경우)
f(N /2) -1 (N이 2의 배수인 경우)
0 (N = 1 인 경우)
)
로 정의할 수 있다.
Bottom - up
dp[1] = 0;
for(int i = 2 ; i <= n ; i ++){
dp[i] = dp[i-1] + 1;
if( i % 2 == 0){
dp[i] = Math.min(dp[i],dp[i/2] + 1);
}
if( i % 3 == 0)
dp[i] = Math.min(dp[i],dp[i/3] + 1);
}
}Top - Down
private static int f(int n) {
if (n == 1) return 0;
if (dp[n] != -1) return dp[n];
int result = f(n-1) + 1;
if(n % 2 == 0){
result = Math.min(result, f(n / 2) + 1);
}
if(n % 3 == 0){
result = Math.min(result, f(n / 3) + 1);
}
dp[n] =result;
return result;
}풀어볼 기본 문제
백준 9465번 스티커
백준 2295번 동전
백준 10844번 쉬운 계단수
백준 1699번 제곱수의 합
백준 11726번 2xn 타일링
백준 11727번 2xn 타일링 2
백준 12865번 평범한 배낭 중요!
백준 16500번 문자열 판별 중요!
백준 11055번 가장 큰 증가 부분 수열 중요!
출처
동적 계획법(Dynamic Programming)
알고리즘 - Dynamic Programming(동적 계획법)
