구간합 구하기 5

1차원 누적합
먼저 일반적인 1차원 누적합을 이용하면 다음과 같이 풀이할 수 있습니다.
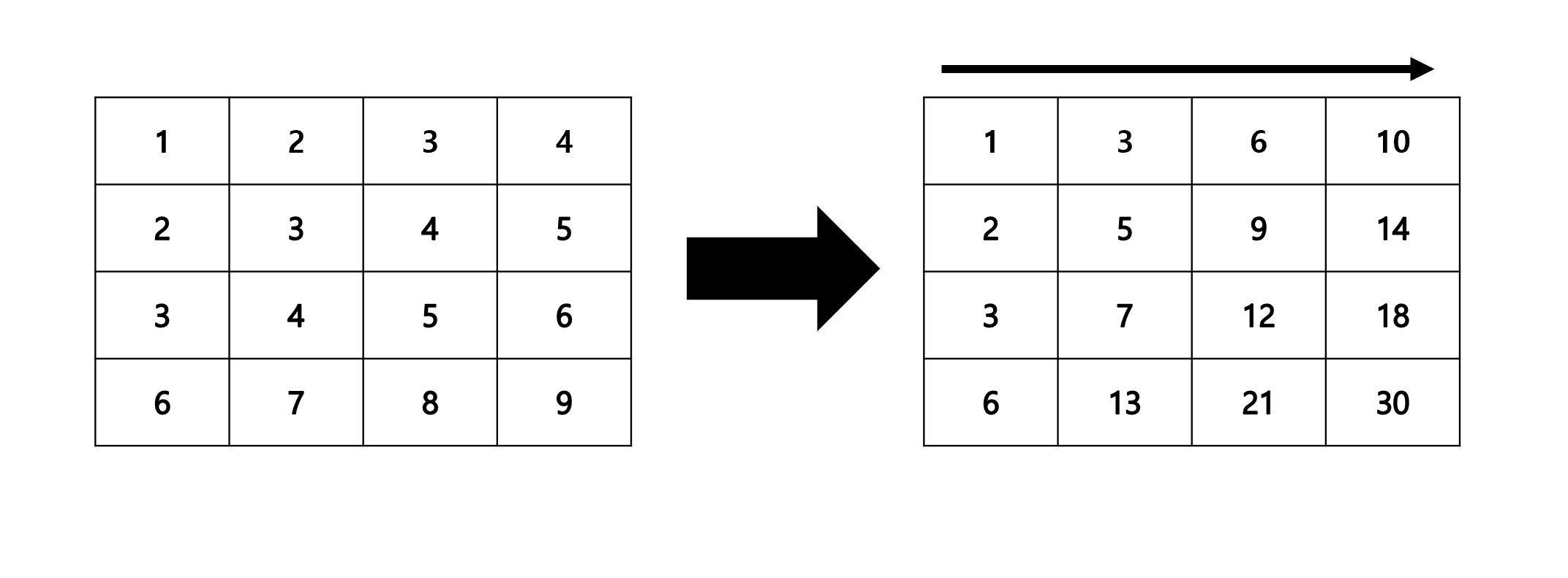

먼저 가로 방향으로 누적합을 구하면 다음과 같습니다.누적합 배열을 S라고 하고
(2,2) 부터 (3,4)까지의 합을 구하려면 다음과 같이 구할 수 있습니다.
S[2][4]-S[2][2-1] + S[3][4]-S[3][2-1]
만약 쿼리가 Q개, 행의 길이가 R이라 고 할 때 시간 복잡도는 O(QR) 입니다. 주어진 문제에서는 O(10^3 * 10^5) = O(10^8) 으로 주어진 시간안에 풀 수 없습니다.
2차원 누적합
따라서 위 문제는 누적합 개념을 2차원으로 확장해서 풀어야 합니다.
2차원 누적합은 S[x][y]는 S[1][1] ~ S[x][y] 범위에 있는 수의 합을 의미합니다.
예를 들어 (3,3) ~ (5,5) 사이에 있는 수의 합을 구하기 위해서는 다음과 같이 구할 수 있습니다.
S[5][5] - ( S[3-1][5] + S[5][3-1] ) + S[3-1][3-1]
전체에서 노란색 영역과 초록색 영의 값을 빼준 뒤 겹치는 부분을 다시 더해주면 됩니다.
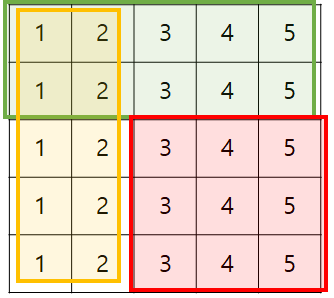
(X1 <= X2 , Y1 <= Y2)
(X1,Y1) ~ (X2,Y2) =S[X2][Y2] - ( S[X-1][Y2] + S[X2][Y1-1] ) + S[X1-1][Y1-1]
(1,1) ~ (X,Y) 까지 누적합 구하기
예를 들어 (1,1) ~ (4,4) 까지의 합을 구하기 위해서는 위에서 했던 방식과 비슷하게 파란색 영역과 초록색 영역을 더한 뒤 겹치는 부분을 빼고 ARR[4][4] 값을 더해주면 된다.
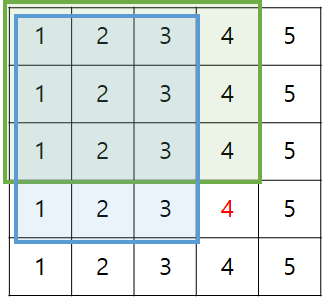
S = [ [0 for _ in range(c+1)] for _ in range(r+1)]
for i in range(1,r+1):
for j in range(1,c+1):
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + ARR[i][j] 전체 코드
import sys
def get2dPrefixSum(x1,y1,x2,y2):
return S[x2][y2] - ( S[x1-1][y2] + S[x2][y1-1] ) + S[x1-1][y1-1]
N,M = map(int,sys.stdin.readline().split())
ARR = [ list(map(int,input().split())) for _ in range(N)]
S = [ [0 for _ in range(N+1)] for _ in range(N+1)]
for i in range(1,N+1):
for j in range(1,N+1):
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + ARR[i-1][j-1] # ARR[i][j] 의미상 i, j 번째 원소
for _ in range(M):
x1,y1,x2,y2 = map(int,sys.stdin.readline().split())
print(get2dPrefixSum(x1,y1,x2,y2))
