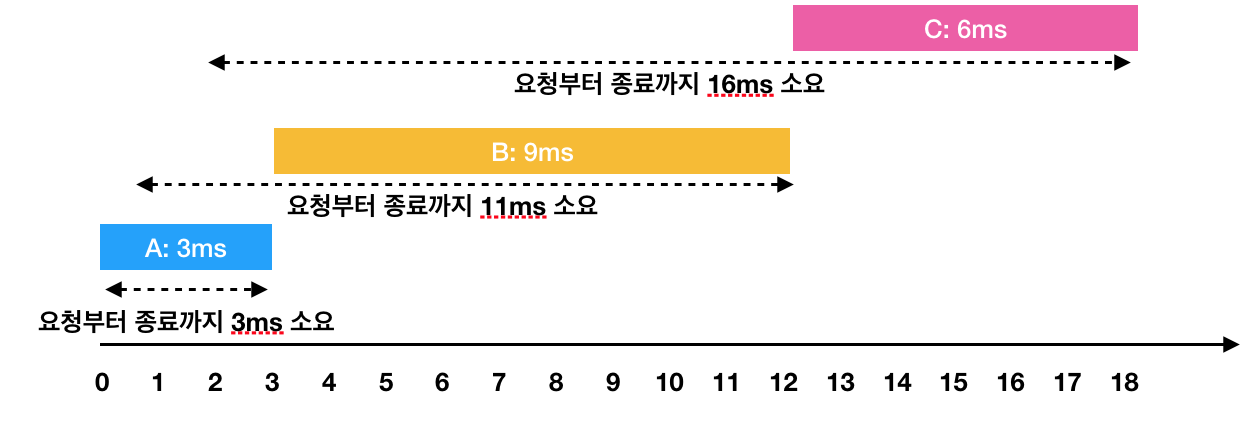
해당 문제에서 가장 중요한 부분은 어떻게 하면 대기 시간을 효율적으로 줄 일 것인가부터 시작한다. 예시에서도 볼 수 있는 것 처럼 두 경우 모두 끝나는 시간은 18초로 결국에는 모두 동일하다.
띠라서 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이기 위해서는 대기 시간을 줄여야 한다는 것이다.
또한 이 문제에서 또 한 가지 키포인트가 있는데 디스크가 쉬고 있으면 안 되는 것이다. 일이 있는 한 무조건 해야 한다는 것이다.
이 부분을 잘 기억하고 있자.

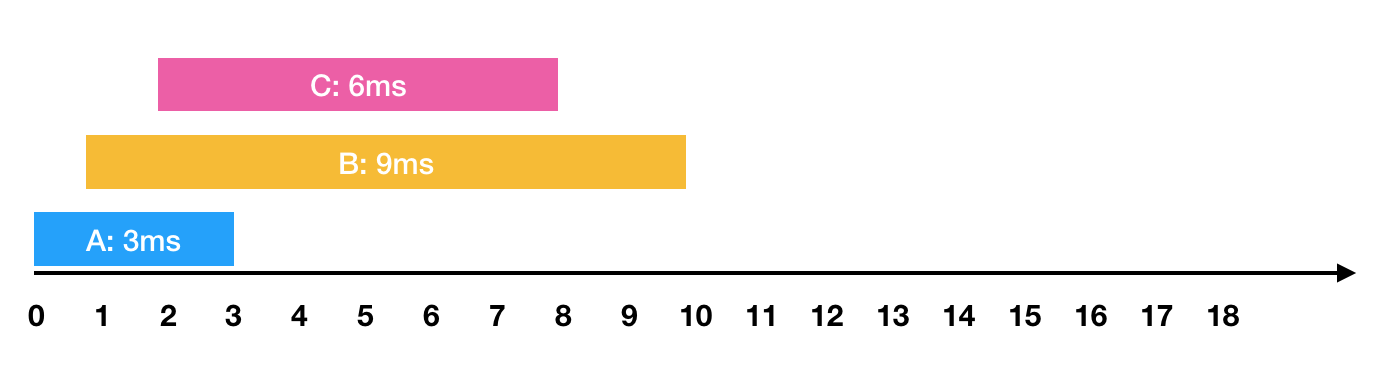
이 문제를 푸는 나의 사고는 다음과 같았다.
가장 먼저 무조건 처음 시작할 때는 가장 먼저 요청이 들어온 잡을 실행할 것이다. 그렇게 되면 예시에서 A가 가장 먼저 실행 될 것이다. 그렇게 되면 A는 3초에 끝나고 3초 시점에 무조건 B와 C 중에 하나를 선택해서 실행해야한다. 이 때 무엇을 선택하야할까? 이게 이 문제의 키포인트다. 앞에서 대기시간을 줄이는 방향으로 잡을 골라야 한다. 이 때 현재 3초인 시점에서 B와 C 중 어느 것을 선택해도 지금까지 기다린 시간( B : 3 - 1 = 2ms ,C : 3 - 2 = 1ms ) 은 무조건 적으로 대기해야하는 시간이다. 따라서 둘 중 소요 시간을 짧은 것을 골라야 선택 받지 못 한 다른 일들의 대기 시간이 줄어든다. (즉, 소요 시간이 긴 걸 고르면 선택 받지 못 한 일들이 그만큼 다 기다려야 하기 때문)
이를 좀 더 일반화 하면
만약 수행할 수 있는 작업 a , b, c, d 가 있다고 하자
이때 만약 작업시간이 가장 긴 a를 수행하게 되면 시작시간과 상관없이 b, c, d 가 기다리는 시간이 a의 긴 수행시간을 더해서 기다려야하기 때문에 전체 평균은 증가할 수 밖에 없는 것이다.
반대로 만약 작업시간이 가장 짧은 b를 수행하게 되면
나머지들의 대기시간도 짧아지고, 전체 평균은 이것을 선택함으로써 손해는 없다는 것을 알 수 있다.
https://nsgg.tistory.com/186
따라서 이 문제는 그리디 알고리즘과 자료구조(힙)이 사용된 문제이다. 그리디인 이유는 현재 상황에서 가장 큰 이윤을 좇아야 하기 때문이고,
탐욕 선택 속성(Greedy Choice Property) : locally optimal choice lead to a globally optimal solution.
최적 부분 구조(Optimal Substructure) : the optimal solution to a problem incorporates the optimal solution to subproblems.
그리디 공부하러가기
다음과 같은 그리디 알고리즘의 속성을 만족한다.
또한 자료구조(힙)이 사용되는 것은 우선순위큐 즉, 최소힙을 사용해서 대기 중인 일 중 소요시간이 최소인 잡을 구해야하기 떄문이다.
from heapq import heappush,heappop
def solution(jobs):
answer = 0
jobs.sort(key= lambda x : (x[0],x[1]))
prev_end_time = -1
end_time = 0
heap = []
i = 0
now = 0
while i < len(jobs):
for j in jobs:
if prev_end_time < j[0] <= end_time:
heappush(heap,(j[1],j[0]))
if len(heap):
cost, start_time = heappop(heap)
prev_end_time = end_time
answer += (cost + end_time-start_time) # 수행시간 + 대기시간
end_time += cost
i += 1
else:
end_time += 1
answer = answer // len(jobs)
return answer
# [[0, 3], [1, 9], [2, 6]]
# [1,9] , [2,6] 요청이 왔을 때 어떤 것을 처리하는 게 효율적인가?
# 실행시간은 같기 때문에, 대기 시간을 줄여야함
# 잡1이 끝난 시점에 잡2,잡3을 할 수 있다. 이 때 다른 일들의 대기시간을 최소화 할 수 있는 방# 법은 소요시간이 가장 짧은 것을 수행해서 최소한 대기시간을 줄이는 것
