분할정복
분할 정복 알고리즘(Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이다. - 위키피디아-
즉 문제를 내가 해결 할 수 있는 수준까지의 작은 문제로 나누어(재귀에서 Base Case) 문제를 해결하고 (Conquer) 하고 그 결과를 합쳐 다시 큰 문제를 해결해 나가는 방식입니다.
조금 더 쉽게 풀어서 말하자면 말 그대로 주어진 문제를 여러 부분 문제들로 나누는데, 작아지면 작아 질수록 풀기 쉬워지는 성질을 이용합니다. 또한 문제의 크기가 엄청 나게 작아져서 (N = 1 or N = 2 정도) 바로 답을 구할 수 있는 수준이 되고, 이것이 재귀에서 Base Case에 해당합니다. 이런 Base Case의 답을 이용해서 각 문제의 답을 구하고, 그 문제들을 불렀던 좀 더 큰 문제를 비교적 간단한 연산처리를 해주면 좀 더 큰 문제 또한 해결 할 수 있습니다. 이렇게 이를 반복해서 첫 문제까지 올라가다보면 결국 최종 정답을 구할 수 있습니다.
분할정복의 핵심 원리
Step 1. Divide
큰 문제를 동일한 타입의 하위 문제로 분할한다.
Step 2. Conquer
재귀적으로 문제를 해결한다.
Step 3. Merge
해결된 문제를 사용(병합)해 큰 문제를 해결한다.
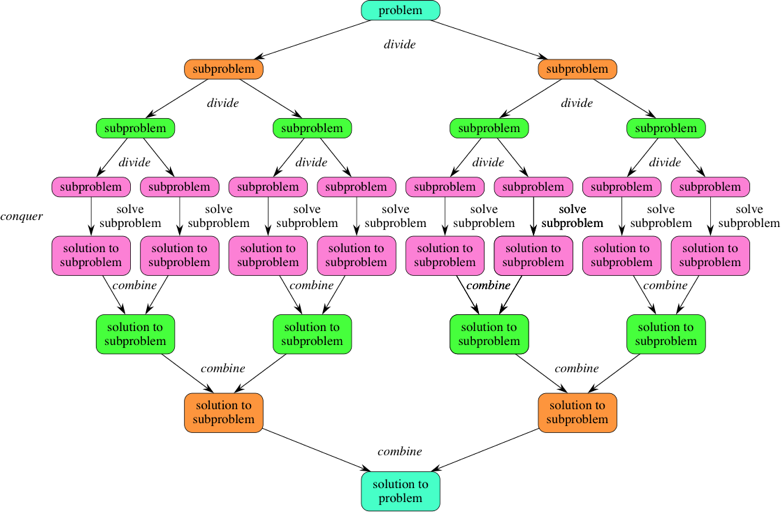
분할정복의 원리는 크게 3가지 단계로 이루어져 있습니다. 위 그림에서 볼 수 있듯이, 맨 위에 있는
(여기서 이용한 다는 것은 다양한 연산 처리를 의미하는데 보통 Merge 혹은 Combine한다고 표현합니다.)
예시) 병합정렬

Step1 Divide
전체 데이터를 반으로 지속적으로 분할 합니다. 언제까지? 직접 문제를 해결 할 수 있는 수준까지. 바로 문제의 크기가 1이 될 때까지.
Step2 Conquer
문제의 크기가 1이 되면 자연스럽게 정렬된 상태이기 때문에, 그 자체로 문제가 해결 됩니다.
Step3 Merge
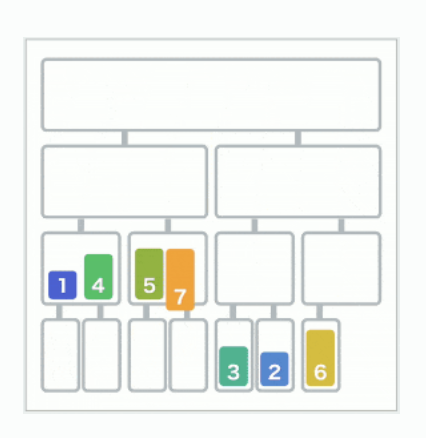
이 해결된 문제들을 합쳐 문제의 크기가 좀 더 큰 문제를 해결합니다. 밑에 이미지를 보면 3과 2를 비교하여 정렬 합니다. 그렇게 되면 문제의 크기가 2인 문제를 해결할 수 있게 됩니다.
따라서 이 과정을 반복해서 위로 올라가면 전체 배열을 정렬할 수 있게 됩니다.
public class MergeSort{
public static void main(String[] args){
int[] arr = new int[100];
for(int i=0; i < arr.length; i++){
arr[i] = (int)(Math.random() * 100);
}
mergeSort(arr, 0, arr.length-1);
for(int i=0; i < arr.length; i++){
System.out.print(arr[i] + ", ");
}
}
public static void mergeSort(int[] arr, int start, int end){
if(start == end) return;
int mid = (start+end)/2; //Divide
mergeSort(arr, start, mid); //Conquer
mergeSort(arr, mid+1, end); //Conquer
//Merge
int[] temp = new int[end-start+1];
int idx = 0;
int left = start;
int right = mid+1;
while(left <= mid && right <= end){
temp[idx++] = arr[left] <= arr[right] ? arr[left++] : arr[right++];
}
while(left <= mid){
temp[idx++] = arr[left++];
}
while(right <= end){
temp[idx++] = arr[right++];
}
for(int i=start; i <= end; i++){
arr[i] = temp[i-start];
}
}
}시간복잡도
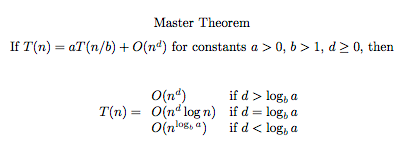
분할 정복의 시간복잡도를 일반화한 마스터 이론은 다음과 같습니다. 원리는 찾아보시면 크게 이해하는데 어렵지 않습니다.
a는 나누어지는 문제의 개수
b는 분할 후 문제의 크기
d는 각 문제마다 병합(정복)하는 단계에서 걸리는 시간
병합 정렬 같은 경우 a = 2 ,b = 2 ,d = 1 이기 때문에 시간복잡도는 O(NlogN)입니다.
분할정복과 DP와의 차이점
분할정복과 DP는 주어진 문제를 작게 쪼개서 하위 문제를 해결하고 그 해답을 이용해서 문제를 해결한다는 점은 같습니다.
차이점은, 분할정복은 분할된 하위 문제가 동일하게 중복되는 일이 일어나지 않는 경우에 사용되며, 중복되는 경우에는 DP를 사용합니다.
그리고 또한 문제를 쪼갤 때 작아진 문제의 크기가 분할정복 같은 경우에는 지수적으로 줄어들지만, DP같은 경우에는 선형적으로 줄어들게 됩니다.
