알고리즘 5일차 - O(nlogn) 정렬, 힙과 힙정렬 최대힙, 최소힙 - 2부

살려줘

1. 최소힙과 최대힙

그렇다면 힙은 어떻게 사용할 때 유의미하게 사용할 수 있을까??
그것이 바로 최소힙과 최대힙이다.

최대힙은 힙 원소들 중 가장 큰 값이 맨 위에 있는 것을 의미하며, 최소힙은 반대로 힙 원소들 중 가장 작은 값이 맨 위에 있는 것을 의미한다.

최대힙 또는 최소힙은 부모가 자식보다 큰 값 또는 작은 값을 가지는 자료구조를 의미한다. 따라서, 루트 노드는 가장 큰 값 또는 가장 작은 값을 갖게 된다.

• 최대힙
  
  다음의 모습이 최대힙의 모습이다. 루트 노드(맨 위에 있는 노드)의 값이 가장 큰 값인 123이 나온다. 또한, 부모가 자식보다 큰 값을 갖는 것이 최대힙의 특징이다.

• 최소힙
  
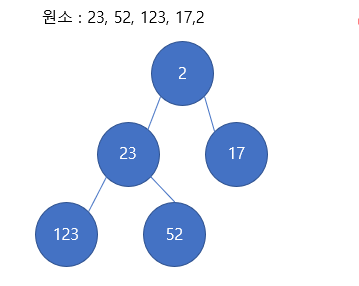
  다음은 최소힙의 모습이다. 역시 부모가 자식보다 작은 값을 갖게 되고, 루트가 가장 작은 값을 갖게 된다.

그런데, 오해하지 말 것은 자식들 간의 관계가 크기 순서대로 정렬된 모습은 아니다. 즉, 위의 최소힙 사진을 보면 23이 17보다 먼저 나오게 된다. 이는 힙의 생성 순서에 따라 달라지게 되는 것이지, 자식들 간의 크기를 비교해서 자식들의 자리를 순서대로 정렬하는 것이 아님을 알 수 있다.
더 직접적으로 이해하기 위해서는 최대힙의 생성, 즉 원소의 추가를 보면된다.

2. 최대힙 또는 최소힙의 원소 추가

이전 힙 - 개요 시리즈부터 계속해서 말해왔던게 있다. 힙은 뭐다??? 힙은 트리이자 완전 이진 트리이다. 완전 이진 트리의 특징은 무엇인가?? 바로 높이가 logn을 유지한다는 것이다. 그렇다면 logn의 높이를 유지하기위해 힙은 어떤 조건을 갖고 있었나??

힙은 부모가 i 번째 인덱스에 있다면, 자식은 ix2, ix2+1 번째에 있다(단, i는 1부터 시작할 때), 이는 배열에 노드를 차곡차곡 쌓아놓는다는 의미이고, 또한 트리의 측면에서 본다면 리프 노드 순서대로 노드를 추가한다는 것이다.

다음의 트리에서 노드 1을 추가한다고하면 어디에 넣어야할까?? 위에서 언급한대로 힙은 완전 이진 트리를 유지해야하기 때문에 힙은 강제적으로 리프 노드의 차례대로 노드를 추가한다. 따라서 다음의 모양을 갖는다.

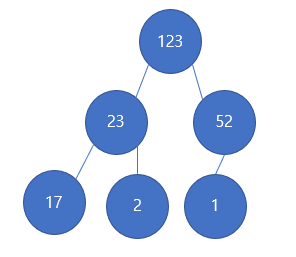
다음의 트리 모양이 될 것이다.

힙의 원소 추가는 이전에 배웠듯이 너무나 간단하다. 그렇다면 최대힙, 최소힙의 원소 추가는 어떨까??

일단 힙의 원소 추가와 같다. 그냥 리프 노드 차례대로 원소를 추가하는 방법을 이용하면 된다. 그런데, 최대힙과 최소힙은 무슨 조건이 있던가??

최대힙과 최소힙은 부모가 자식보다 크거나 또는 작아야한다.

이러한 조건을 만족하기 위해서는 새로운 원소가 추가되면, 자신의 부모와 크기 비교를 해서 부모와 자리를 바꿀지 안바꿀지를 결정해야한다. 만약 새로운 원소가 부모보다 크면, 부모와 새로운 원소의 자리를 바꾸어준다. 그리고 이 과정을 계속해서 반복해주면 된다.

가령 최대힙에서 노드 151을 추가하는 예제를 보도록 하자

노드 151을 추가하려고 한다. 힙은 완전 이진 트리를 유지하기위해서 리프 노드 차례대로 원소를 추가한다. 따라서 52의 왼쪽 자식으로 151노드를 추가한다.

그런데, 151노드를 추가하고 나니까, 최대힙의 조건을 위반하게된다. 즉, 151은 52노드의 자식인데 151노드가 52노드보다 더 큰 값을 갖고있기 때문이다. 따라서, 이들을 교환해주어야한다.

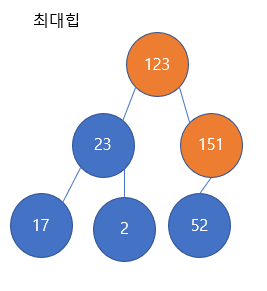
52노드와 151노드를 교환하고 난 모습이다. 교환 후 끝나는 것이 아니라, 또 다시 부모와 비교를 한다. 이 역시 최대힙의 조건을 위반한다. 151의 부모가 123이고 123이 151보다 작기 때문에 부모가 자식보다 더 커야한다는 최대 힙의 조건을 위반하여 교환(swap)이 이루어진다.

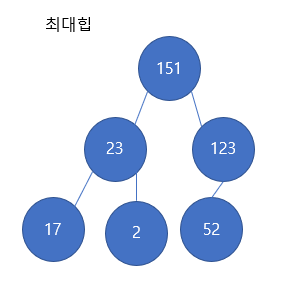
최종적으로 다음과 같은 최대 힙의 모습이 만들어지게된다. 모든 부모가 자식보다 큰 값을 갖게 되고 힙의 구조를 유지하게 되는 것이다.

참고로, 최소힙은 반대로 부모 < 자식 이기 최대 힙의 로직에서 부호만 바꾸어주면 된다.
우리는 위의 과정을 heapify라고 부른다. (최대 또는 최소)heap을 만드는 과정이라고 생각하면된다. 원소 하나가 추가되면, 해당 원소를 기준으로 heapify를 시켜주면 최대 또는 최소 힙을 만드는 과정을 반복하게 된다. 즉, 부모와 자식의 값을 비교하여 바꾸어주거나 또는 반복을 종료하는 연산을 수행한다.

따라서, 우리는 최대힙 또는 최소힙을 만들기 위해 원소들을 추가할 때마다 heapify를 실행해주면 되는 것이다. heapify 연산은 잘보면 최대가 트리의 높이이다. 즉, logn 시간이 걸린다는 것이다. 왜냐하면 리프(바닥)부터 부모와 비교하여 올라오면 부모와 비교하는 것이 최종 연산이 되는데, 이것은 트리의 높이와 비례하기 때문이다.

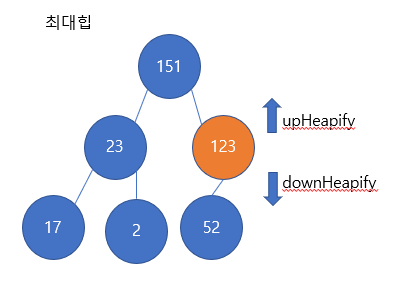
하지만, heapify는 두 가지로 나뉘게 되는데, upHeapify와 downHeapify이다.
upHeapify는 위에서 본 것과 같이 아래에서부터 위로 부모와 비교하여 올라가는 것을 의미하고, downHeapify는 아직 예제로 보여주진 않았는데, 해당 원소에서 아래로 heapify를 실행하는 것이다. 따라서 자신의 자식들과 값을 비교하여 내려가는 방향이다.

일단 upHeapify를 이용하여 최대힙을 만드는 코드를 만들어보자

• 최대힙 만들기

#include <iostream>

using namespace std;

//첫번째 원소 0은 없는 값이라고 생각
int data[11] = {0,32,53,61,1,2,100,42,58,98,72};
int n = 10;
int heap[11];
int size = 0;

void swap(int *data1, int *data2){
    int temp = *data1;
    *data1 = *data2;
    *data2 = temp;
}

void upHeapify(int index){
    int parent = index/2;
    while(parent >= 1){
        if(heap[parent] > heap[index]) return;
        swap(heap[parent], heap[index]);
        index = parent;
        parent = index/2;
    }
}

void addNode(int data, int index){
    heap[index] = data;
    upHeapify(index);
    size++;
}
int main(){
    for(int i = 1; i <= n; i++){
        addNode(data[i],i);
    }
    for(int i = 1; i <= size; i++){
        cout << heap[i] << ' ';
    }
}

다음 처럼, upHeapify를 통해서 최대힙을 만들 수 있다. 최종적인 모습은 다음과 같은 결과가 나온다.

100 98 61 58 72 53 42 1 32 2 

이를 그림으로 표현하면

이런 모양이다. 위의 코드를 통해서 Heapify로 최대 힙 또는 최소 힙을 만들 수 있고, 원소가 추가되면 upHeapify를 이용하면 된다는 사실을 알게되었다.

그런데, 원소가 삭제되면 어떻게 해야할까??

3. 최대 힙 또는 최소 힙의 원소 삭제

힙에 대한 기억을 삭제해주세요

최대 힙, 최소 힙은 삭제 연산 시에 루트에 있는 원소를 pop하는 연산으로 사용된다. 이유는 간단하다. 최대 힙, 최소 힙은 도대체 언제 사용할까??

이는 정말 중요한 질문인데, 만약 우리가 위의 코드에서 data[] 배열의 최대값을 구하고, 최대값을 data배열에서 삭제하고 또, 다음 최대값을 구하여 data[] 배열을 빈 배열로 만드는 연산을 한다고 생각해보자.

data[] 배열은 길이 n =10이고, 매번 최대값을 탐색하는데 n번의 시간이 걸린다. 따라서 원소가 없을 때까지 최대값을 찾고 없애는 연산을 반복한다면 적어도 O(n^2) 시간이 걸리게 된다.

그런데, 최대힙을 이용하면 어떤가?? 루트 (index = 1)인 곳에 최대값이 항상 위치하게 된다. 그렇다면 루트의 값을 빼내주고 다음으로 큰 원소를 자식들 중에서 올려주는 연산을 해주면 된다.
여기서 루트 원소를 제거하는 연산은 O(1)이고, 최대힙을 유지하기위해 자식들을 올려주는 연산은 heapify이므로 트리의 높이인 O(logn) 시간이 걸린다.

따라서, n번 다음의 연산을 반복하므로 O(nlogn)이 된다. 이는 엄청난 시간 복잡도의 감소이다.
이러한 최대힙, 최소힙의 장점을 이용하기위해 굳이 랜덤 액세스로 데이터를 삭제할 필요가 없고, 루트의 값만 삭제해주면 된다.

그럼 루트의 값을 삭제하고, 자식들을 위로 올리는 heapify를 어떻게해야할까?? 생각만해도 막막하다. 따라서 우리는 다음의 방법을 이용할 것이다.

위의 최대힙 코드에서 heap 데이터를 최대값부터 차근차근 뺀다고 가정하자 그러면 다음과 같은 모습이 된다.

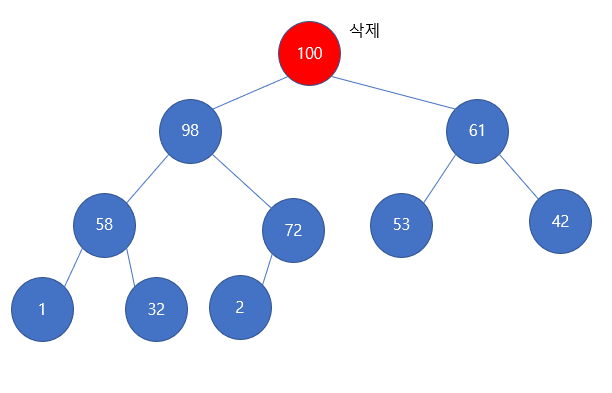
루트 원소인 100을 삭제해야할 것이다. 그런데 막상 삭제하고 보면

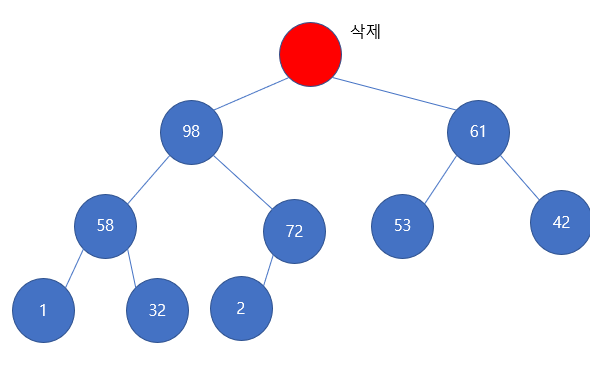
굉장히 허전하다. 마치 애플 로고없는 맥북같은 느낌이다.
또한, 부모값이 사라지므로 자식들과 값을 비교하여 heapify를 하기에 녹록치 않다. 굳이하려면 자식들 간의 비교를 해야하는데 이는 모든 원소들을 비교해야하므로 logn시간안에 해결이 안된다. 따라서 우리는 다음의 방법을 이용하려고 한다.

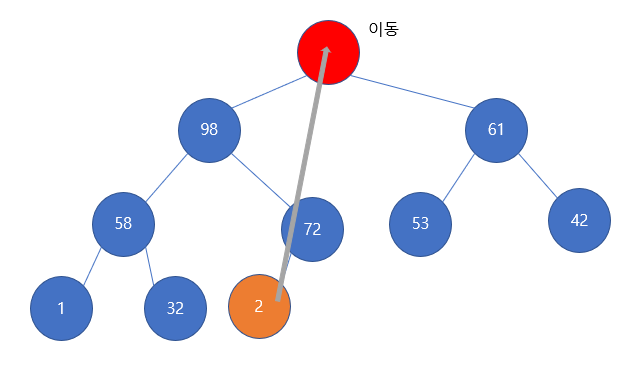
힙의 맨 마지막 원소를 루트로 보내는 것이다. 맨 마지막 원소는 어차피 자식이 없고, 부모보다 작은 값이므로 맨 마지막 원소가 사라져도 문제가 없다.

문제는 다음의 맨 마지막 원소가 루트에 갈 경우 발생한다.

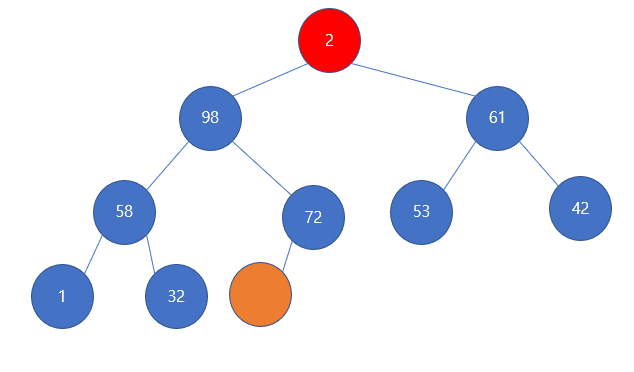
짜잔! 벌써부터 불-편해지는 상황이 발생했다. 루트는 2인데, 루트의 자식이 98, 61인 것이다. 이는 최대 힙의 조건인 부모는 자식보다 커야한다는 조건이 어긋나게 된다. 그런데, 우리는 사 이걸 알고도 맨 마지막 원소를 루트로 올려보낸 것이다.

왜 이런 짓을 했을까?? 비교하려는 값을 두어서 heapify연산을 해주기 위함이다. heapify가 된다면 logn안에 다시 최대힙을 만들 수 있기 때문이다. 그런데 원소의 추가시에는 아래(리프)에서 위(루트)로가는 upHeapify였지만, 여기서는 위(루트)에서 아래(리프)로가는 downHeapify가 발생한다. 결론적으로는 방향의 차이만 있지, 해주는 역할과 시간복잡도는 똑같다.

즉, 부모 기준에서 자식들과 비교하여 자신보다 큰 값을 위로 올린다. 여기서 자식들 중에 만약 2개 모두 부모보다 큰 값을 갖는다면, 이는 임의로 처리해도 된다. (필자는 더 큰 자식을 위로 올리도록 구현할 것이다)

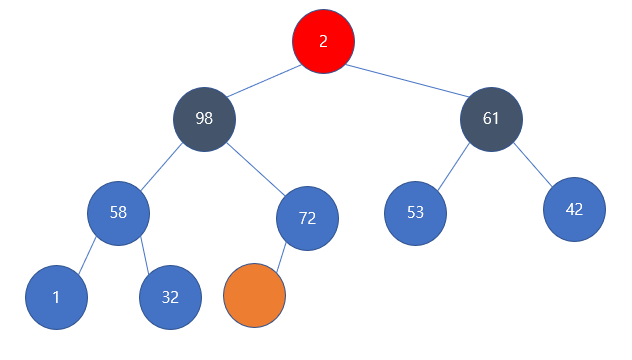
루트인 2를 기준으로 좌우 자식들과 값을 비교하도록 하자, left와 right모두 부모보다 크므로 swap하도록 한다. 여기서 left가 right보다 더 큰 값을 가지므로 left를 기준으로 루트값과 change하도록 하겠다.

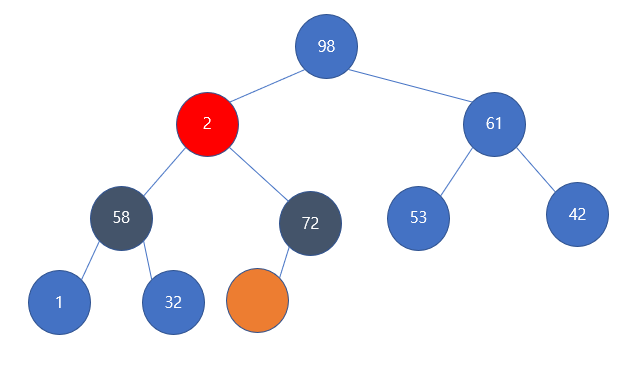
이렇게 되었다. 이제 빨간색으로 표시한 곳으로 2가 내려왔다. 2는 이제 또 자신의 자식들과 값 비교를 해야한다. 58, 72로 모두 자신보다 크므로 더 큰 값을 가지는 right로 swap한다.

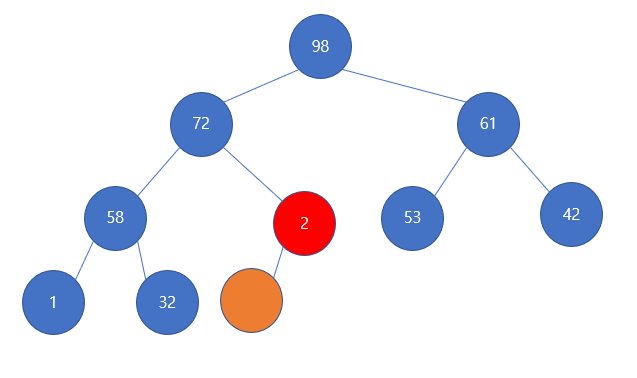
다음의 모양을 갖게되고, 2는 더 이상 비교할 자식이 없다. 주황색으로 표시한 노드는 이전에 맨 마지막 원소가 있던 노드로 루트로 보내졌기 때문에 삭제하면 된다.

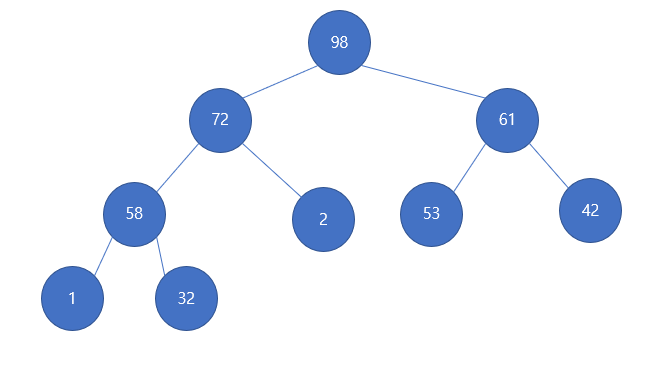
다음과 같이 최대힙이 유지되게 된다.

이렇게 힙의 삭제 연산까지 보게되었다.
그런데, 마지막 원소는 어떻게 삭제할까?? 아주 간단하다. 힙의 사이즈를 줄이면 된다.
이는 코드를 보면 더욱 간단하다는 사실을 알 수 있다.

코드

#include <iostream>

using namespace std;

//첫번째 원소 0은 없는 값이라고 생각
int data[11] = {0,32,53,61,1,2,100,42,58,98,72};
int n = 10;
int heap[11];
int size = 0;

void swap(int *data1, int *data2){
    int temp = *data1;
    *data1 = *data2;
    *data2 = temp;
}

void upHeapify(int index){
    int parent = index/2;
    while(parent >= 1){
        if(heap[parent] > heap[index]) return;
        swap(heap[parent], heap[index]);
        index = parent;
        parent = index/2;
    }
}

void downHeapify(int index){
    int left = index*2;
    while(left <= size){
        int right = left+1;
        if(right <= size){
            if(heap[left] < heap[right]) left = right;
        }
        if(heap[left] < heap[index]) return;
        swap(heap[index], heap[left]);
        index = left;
        left = index*2;
    }
}

void addNode(int data, int index){
    heap[index] = data;
    upHeapify(index);
    size++;
}

int pop(){
    int root = heap[1];
    heap[1] = heap[size];
    size--;
    downHeapify(1);
    return root;
}
int main(){
    for(int i = 1; i <= n; i++){
        addNode(data[i],i);
    }
    cout << "push ";
    for(int i = 1; i <= size; i++){
        cout << heap[i] << ' ';
    }
    cout <<'\n' <<"pop : ";
    while(size){
        cout << pop() << ' ';
    }
}

하나하나 살펴보면 다음과 같다.

int pop(){
    int root = heap[1];
    heap[1] = heap[size];
    size--;
    downHeapify(1);
    return root;
}

POP은 루트의 원소 삭제 연산이다. 먼저 우리는 힙을 1부터 시작하도록 하였으니까, root는 1번째 인덱스에 있게 된다. 따라서 heap[1]로 root를 가져오고, 위에서 보았듯이 루트에 가장 마지막 원소를 넣는다. hepa[1] = heap[size]를 넣는 것이다. 참고로 size는 0부터 시작하기 때문에 일반적으로 우리가 넣는 heap가 size차이가 1정도 난다. 따라서 size가 힙의 인덱스보다 -1작다는 사시을 인지하고 넘아가자

이제 맨 마지막 원소를 루트에 넣어주었으니 맨 마지막 원소를 삭제해준다. 해당 연산이 size--이다. 자연스럽게 사이즈를 줄여 맨 마지막 원소를 없앴다고 보는 것이다. 다음으로는 downHeapify를 해준다. 루트부터 차근차근해야하므로 root인 1을 넣어주도록 한다.

void downHeapify(int index){
    int left = index*2;
    while(left <= size){
        int right = left+1;
        if(right <= size){
            if(heap[left] < heap[right]) left = right;
        }
        if(heap[left] < heap[index]) return;
        swap(heap[index], heap[left]);
        index = left;
        left = index*2;
    }
}

downHeapify는 upHeapify보다는 어렵다. 그러나 내부로직을 보면 그렇게 어렵진 않다. 일단 파라미터로 들어온 index는 부모와 같은 역할이다. 따라서 자식인 left 는 index의 2를 곱한 값이 되고, right는 2를 곱하고 1을 더한 값과 같다.

left = parent(index) x 2;
right = parent(index) x 2+ 1 = left + 1;

과 같다. 따라서, 우리는 left먼저 체크해준다.
while문은 left가 size랑 같거나 작다라는 의미인데, 이는 parent가 자식이 있는 것인가를 의미한다. 만약 자식이 있다면, right와 left중에 누가 더 큰 값인 지 결정하여 left에 저장하도록 한다.

그 다음 부모와 자식들을 비교하여 swap해주고 이를 아래로 쭉 리프노드까지 반복해주면 된다.

결과는 다음과 같다.

push 100 98 61 58 72 53 42 1 32 2 
pop : 100 98 72 61 58 53 42 32 2 1 

pop을 한 결과를 보면 큰 수부터 차례대로 나온 것을 볼 수 있다. 아주 신기하고 재밌다.

자 이제 힙정렬이 끝났다
?????????????????????????
의문이 들 수 있겠지만, 위의 pop과정을 보면 된다.
pop의 결과값들을 보자, 그러면 내림차순으로 정렬된 것을 볼 수 있다.
만약 최소힙으로 pop을 했었다면 오름차순으로 정렬된 것일 것이다.

이 처럼 최대힙과 최소힙의 원리인 부모가 자식보다 크다 또는 작다를 이용하고, logn 이라는 트리의 높이를 유지하는 특성을 이용하여 정렬하는 것이 바로 힙정렬이다.

모든 원소마다 pop을 해야하고, pop연산 시에 heapify가 필요하므로 시간복잡도는 자연스럽게 O(nlogn)이 된다.

결국 원소의 삭제(pop)과 heapify를 통해 값을 정렬하는 것이 힙정렬인 것이다.
뭔가 서론만 아주 길게하고, 본론은 한 두 줄 안에 끝나는 느낌이지만 정말 이게 전부이다.

이렇게 우리는 트리에서부터 힙정렬까지 다 배웠다. 기억해야할 것은 다음과 같다.

1. 힙은 완전 이진 트리이므로 높이가 logn인 트리 형상을 유지한다.
2. 힙의 자식은 부모의 인덱스가 i라면 left = ix2, right = ix2+1 인덱스를 갖는다.
3. 반대로 자식의 인덱스가 i라면 부모는 i/2 인덱스를 갖는다.(단, 소수점은 버린다)
4. 힙 생성 시, 또는 힙 원소 추가 시에는 맨 마지막에 원소를 넣고 upHeapify를 수행한다.
5. 힙에서 원소를 삭제 시에는 루트에서 원소를 pop하고, 맨 마지막 원소를 루트에 넣고 downHeapify를 수행한다.
6. heapify는 트리의 높이에 비례하므로 시간복잡도 O(logn)시간을 갖는다. 따라서 n개의 원소를 pop하는데 필요한 시간은 O(nlogn)이므로 힙정렬은 시간복잡도 O(nlogn)시간을 갖는다.

이게 전부이다. 그러나 여기서 끝나면 재미가 없다. 이럴꺼면 c++ stl중에 priority_queue를 가져다쓰면 되지~~ 라고 생각할 것이다.

필자의 아주 지극히 개인적인 소견인데, 필자는 웹 개발을 하다가, 블록체인을 하다가, 린공지능을 하다가 현재는 하다하다 C/C++로 임베디드와 서버 개발을 하고있다. 이렇게 살다보니 느낀 것은 어떤 도메인에 대한 기술적 지식이 크게 중요하지 않다는 것을 느꼈다. 물론 깊은 이해를 필요로하는 부분이 있긴하지만, 대부분이 이리치이고 저리치이면서 개발하고 구글링하다보면 이해도 되고 개발도 어느정도 된다. (여기서 말하는 기술적 지식의 영역은 박사 수준의 영역까진 아니라고 생각하면 된다.) 그러나, 한 가지 중요한 역량이 있는데, 그래서 그 기술을 어떻게 내가 구현할 꺼냐는 것이다.

가령 DB에서 데이터를 받아서 가장 우선순위가 높은 것을 뽑아주도록 한다고 하자, 그럼 초짜는 일단 DB에서 데이터를 받아오고 우선순위대로 정렬해주는 api를 이용하여 짠하고 만들어지면 끝! 이라고 생각한다. 여기서 한 발 더 나아간 사람은 우선순위가 변하면 어떻하지? 를 생각하고 변할때 다시 api를 호출해주는 코드를 만든다. 여기서 더더더더더더더 나아간 사람은 우선순위대로 정렬하는 api 코드를 뜯어본다. 그리고 깨닫게 된다. 아! 이거 힙정렬이구나, 그런데 데이터의 우선순위가 하나만 바뀐다고해서 전체를 힙정렬해야한다고? 이건 좀... 하면서 api에 오버로드를 하여 자신의 로직을 한 줄 추가한다. 그리고 그 로직 한 줄로 서버 성능이 크게 좌우된다.

필자는 기술적 지식이 높은 사람을 까내리려고 이런 말을 하는 것은 아니다. 다만, 요즘 너무 기술적 지식에 치우쳐 제대로 구현할 줄 아는 능력이나 사고력을 보는 면접이 많이 사라진 것 같아 아쉬울 따름이다. 개발자로 취업한다고 학생들이 스프링 붙잡고 공부하는 모습을 보면 정말 많이 안타깝다. 그러나, 세상이 뭐 이런데 어떻게 하겠나 어쩔 수 없는 것이라 아쉽다.

그래서, 각설하고 최대힙에서 만약 하나 노드에서 값이 바뀌면 어떻게 해야할것인가? stl에서는 새로 최대힙을 만들 수 밖에 없다. 그러나, 우리가 직접 힙을 만들거나 stl을 변형한다면 두 번의 heapify를 통해 해결할 수 있고 O(nlogn)시간이 걸릴 것을 O(logn)안에 해결할 수 있다.

4. 최대 힙 또는 최소 힙에서의 특정 데이터 변경

만약 최대 힙, 최소 힙에서 노드의 k값을 변경해야한다고 한다면 어떻게해야할까? 생각보다 간단하다. k값을 갖는 노드의 데이터를 변경해주고 heapify를 up, down 차례대로 해주면 된다. down, up순서로 해도 상관없다.

k값을 갖는 노드를 찾는데 O(n) 시간이 걸리고, heapify에 O(logn) 시간이 걸리므로 총, O(n)시간이 걸리게 된다. 다만, 특정 값이 어디 인덱스에 있는지 mapper로 기억해놓으면 O(1)시간안에 K값을 갖는 노드를 찾을 수 있으므로 O(logn)에 구현도 가능하다. 물론 이 때에는 data값의 범위를 알고 있을 때이다.

굉장히 간단한 구현이지만, 힙에 대해서 잘 모르거나 한 번도 구현해본 적 없는 사람은 손도 못대고 다른 방법을 생각하려고 한다. 이제 배웠으니 한 번 구현해보자

이전에 예제로 썼던 최대힙 예제를 가져와보자

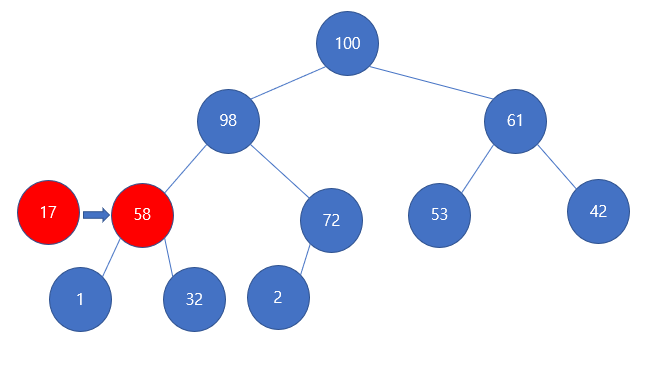
자 노드 58를 노드 17로 바꾸어보자, 그러면 최대힙이 무너지게 되므로, upHeapify와 downHeapify를 해주어야 한다.

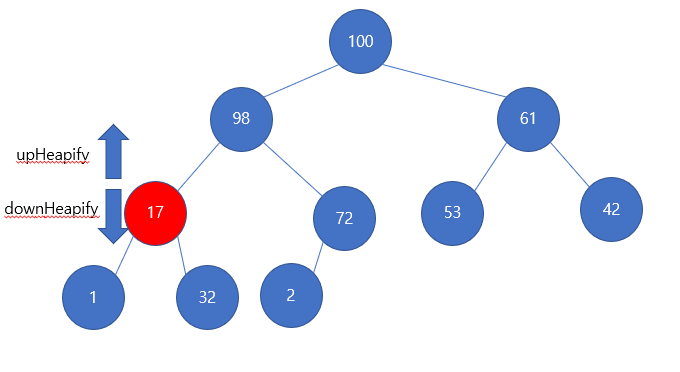
바로 이렇게 해주면 된다.
upHeapify 시에는 17이 98과 만나서 부모보다 작으므로 순회가 종료된다.
downHeapify 시에는 17의 자식이 1, 32이므로 32보다 자신이 작으므로 swap한다.

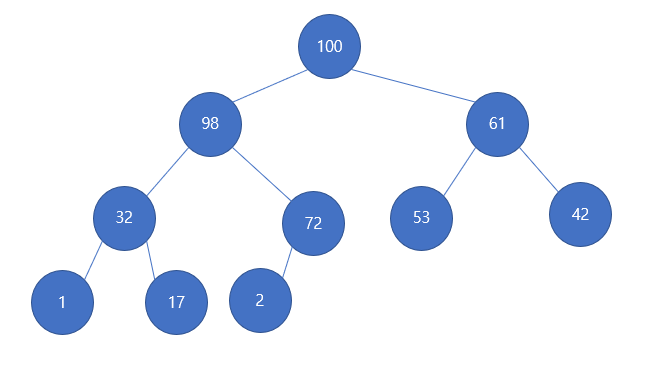
다음과 같은 모습으로 힙에 저장될 것이다.

그렇다면 코드로 확인해보도록 하자

#include <iostream>

using namespace std;

//첫번째 원소 0은 없는 값이라고 생각
int data[11] = {0,32,53,61,1,2,100,42,58,98,72};
int n = 10;
int heap[11];
int size = 0;

void swap(int *data1, int *data2){
    int temp = *data1;
    *data1 = *data2;
    *data2 = temp;
}

void upHeapify(int index){
    int parent = index/2;
    while(parent >= 1){
        if(heap[parent] > heap[index]) return;
        swap(heap[parent], heap[index]);
        index = parent;
        parent = index/2;
    }
}

void downHeapify(int index){
    int left = index*2;
    while(left <= size){
        int right = left+1;
        if(right <= size){
            if(heap[left] < heap[right]) left = right;
        }
        if(heap[left] < heap[index]) return;
        swap(heap[index], heap[left]);
        index = left;
        left = index*2;
    }
}

void addNode(int data, int index){
    heap[index] = data;
    upHeapify(index);
    size++;
}

int pop(){
    int root = heap[1];
    heap[1] = heap[size];
    size--;
    downHeapify(1);
    return root;
}

void change(int from, int to){
    int target = 0;
    for(int i = 1; i <= size; i++){
        if(heap[i] == from){
            target = i;
            break;
        }
    }
    heap[target] = to;
    upHeapify(target);
    downHeapify(target);
}

int main(){
    for(int i = 1; i <= n; i++){
        addNode(data[i],i);
    }
    cout << "push ";
    for(int i = 1; i <= size; i++){
        cout << heap[i] << ' ';
    }
    change(58, 17);
    cout <<'\n' <<"change : ";
    for(int i = 1; i <= size; i++){
        cout << heap[i] << ' ';
    }
}

결과

push 100 98 61 58 72 53 42 1 32 2 
change : 100 98 61 32 72 53 42 1 17 2 

17 노드가 정확히 뒤에서 두 번째에 저장된 것을 확인할 수 있다.

void change(int from, int to){
    int target = 0;
    for(int i = 1; i <= size; i++){
        if(heap[i] == from){
            target = i;
            break;
        }
    }
    heap[target] = to;
    upHeapify(target);
    downHeapify(target);
}

값을 바꾸어주는 코드는 상당히 단순하다. from이 내가 찾는 노드의 값이고, to가 내가 바꾸려는 데이터 값이다. target은 from 데이터가 어떤 인덱스 값을 갖는 지 저장하고, heap[target] = to로 값을 바꾼다.

그 이후로 최대힙 구조를 유지하기위해 target 인덱스를 기준으로 heapify를 실행해준다.
아주 간단한 코드이지만, 이런 코드를 만드냐 못 만드냐에 따라 성능 차이가 심해지고 부하가 많이 줄어든다. 기술을 잘 알고있는 개발자가 되는 것도 좋지만, 개인적으로 이런 기본적인 구현에 있어서 능력이 부족하면 좋은 개발자가 되기에는 힘들다고 생각한다.

모두 즐거운 공부가 되었으면 한다~