힙과 힙정렬

안타깝게도 hip이 아니라, heap이다.

힙정렬을 배우기 전에 힙을 먼저 알아야한다. 정리하자면

힙 = 자료구조
힙정렬 = 알고리즘

으로, 힙이라는 자료구조를 이용한 정렬 알고리즘으 힙정렬이라는 것이다.

0. 트리

트리라고하면 굉장히 어려워보이지만, 힙은 굉장히 단순한 트리구조를 갖는다.
만약, 트리에 대해서 잘 모른다면 이렇게 간단하게 설명하겠다.

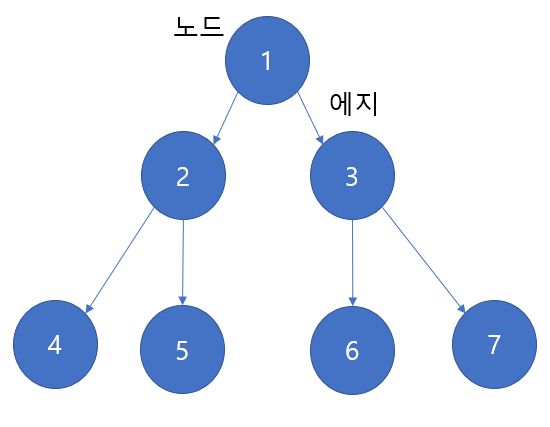
동그랑땡 모양의 데이터가 저장된 것을 노드 라고 부른다.
그리고, 이 노드 간의 상하관계를 나타내는 것을 에지라고 부른다.
또한, 이 노드 중에서 가장 최상위에 있는 노드를 루트라고 한다. 위의 그림에서 루트는 노드 1번이 된다.
반면, 마지막에 있는 노드들을 리프라고 한다. 여기서는 4, 5, 6, 7번 노드들이 리프노드가 된다.

노드와 에지로 연결되어있고, 이들 간의 상하관계를 갖고 있는 것을 트리라고 부른다.
계층 관계(상하관계)가 있는 것이 특징이다.

일반적으로 특정 노드의 바로 하위노드를 자식이라고 부르며, 상위 노드는 부모라고 부른다.

다음과 같이 노드 1번의 자식은 2, 3번 노드이고, 2, 3번 노드의 부모를 1번 노드라고 한다.
이렇게 하나의 노드에 최대 2개의 자식을 갖을 수 있는 트리를 이진 트리라고 한다.

1. 이진 트리(binary tree)

이진 트리는 트리 중에서, 부모가 자식 노드을 최대 두 개만 갖을 수 있는 트리를 말한다.

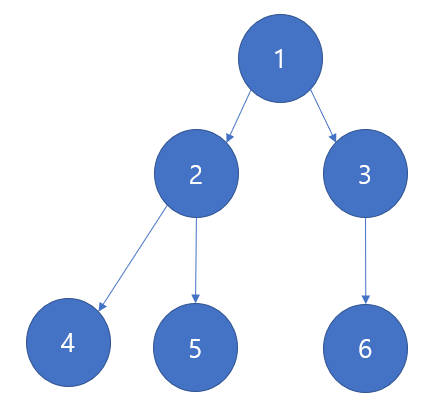
다음과 같은 트리는 이진 트리 형식을 만족한다. 각 노드마다 자식을 최대 2개까지만 둘 수 있기 때문이다. 최대 2개이므로 0개, 1개 ,2개 자식을 두어도 상관없다. 다만 3개 이상부터는 문제가 생긴다.

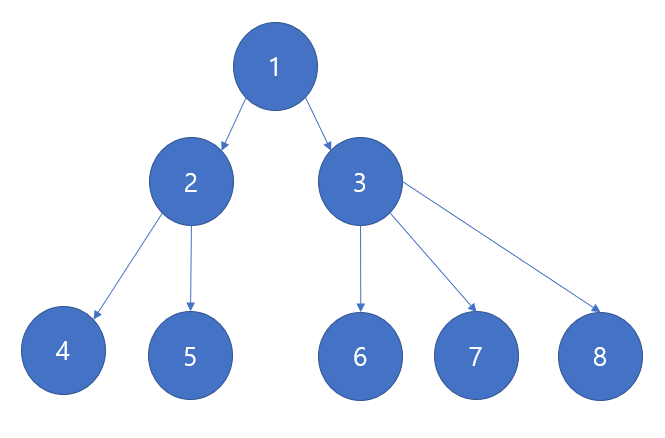
바로 이런 트리는 이진 트리라고 할 수 없고, 그냥 트리 관계를 가진다라고 한다.

이진 트리는 자식을 최대 2개만 둘 수 있으므로, 왼쪽 자식을 left, 오른쪽 자식을 right로 둔다.

다음과 같이 부모가 1번 노드라면 자식은 2, 3번 노드이고, left가 2번 노드, right가 3번 노드가 된다.

이진 트리를 활용하는 방법 중 가장 대표적인 예로는 힙과 이진 탐색 트리가 있다.
우리는 힙을 배울 것이므로, 힙에 대해서 알아보고 이진 탐색 트리에 대해서는 다음에 알아보도록 하자

2. 완전 이진 트리

앞서 말했듯이 힙은 트리이며, 이진 트리이다. 더불어 힙은 완전 이진 트리이다.
완전 이진 트리가 무엇이냐 한다면, 다음의 예를 보자

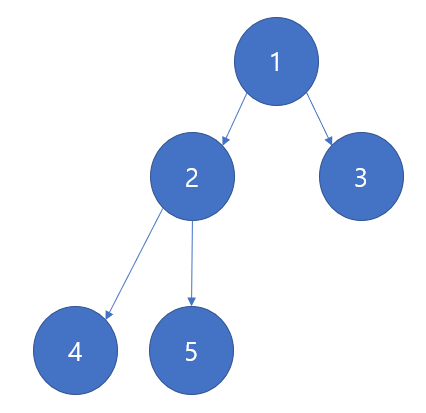
다음의 트리와

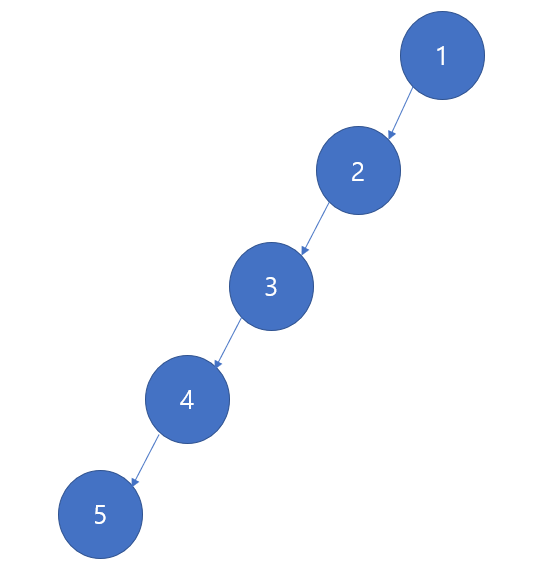
다음의 트리를 비교해보도록 하자

만약 내가 5를 찾아간다고 하자, 첫번째 트리의 모양이 더 탐색에 유용할까 아니면 두번째 트리의 모양이 탐색에 유용할까??

재밌게도 첫번째 트리가 더 좋다. 왜냐하면 트리의 모양이 퍼져있기 때문에 1 -> 2 -> 5 로 탐색하면 되기 때문이다. 그런데, 두번째 트리는 마치 배열마냥 쭉 늘어져 있다. 이는 계층적 관계를 이용하는 트리에서 좋은 효율을 갖지 못한다.

일반적으로 트리의 모양은 노드의 개수와 데이터와 관계가 전혀없다. 따라서 트리의 모양은 결정되어있지 않고, 어떻게 구현하냐에 따라 가지각색의 모양을 갖는다.

그런데 확실한 것은 이진 트리에서 일자로 쭉 되어있는 트리의 모습보다는 위부터 자식을 하나하나 채워서 평평한 트리 모양을 만드는 것이 더 탐색에 좋다는 것을 알 수 있다.
여기서, 탐색에 좋은 이진 트리의 모습으로 높이가 logn을 유지하는 트리를 완전 이진 트리라고 한다.

완전 이진 트리의 단적인 예로 다음이 있다.

만약 왼쪽의 트리에서 노드 6을 추가한다면 어디에 추가하는 것이 좋을까?? 리프 노드는 3, 4 ,5가 있다. 만약 4번 노드에 추가한다면 다음과 같은 모양이 될 것이다.

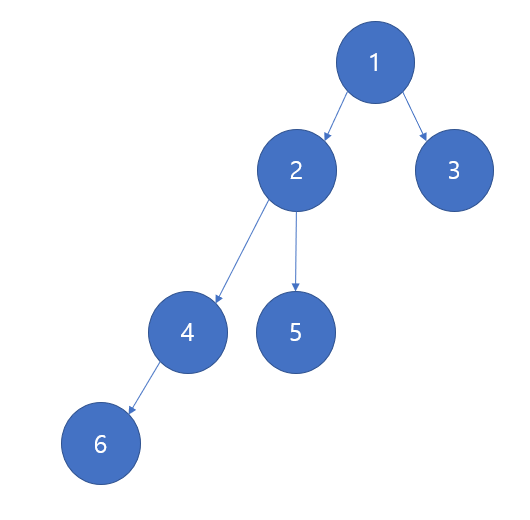
그럼 6번 노드를 탐색한다고 한다면, 다음과 같은 과정을 겪게 된다. 1->2->4->6 총 4번의 과정을 거치게 된다.

그런데 만약 3번 노드에 6번 노드를 추가했다면 다음과 같이 된다.

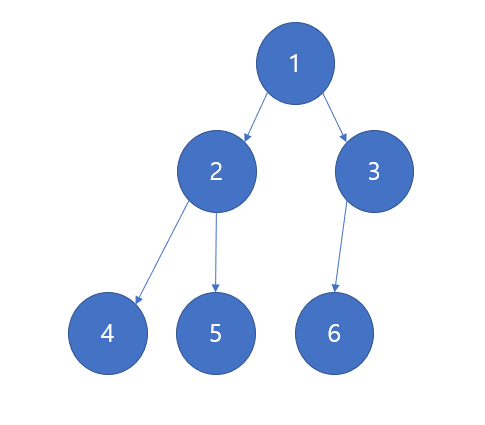
바로 이런 모양이 된다. 6번 노드를 탐색한다면 1->3->6으로 총 3번의 과정만 거치면 된다.
이렇게 리프 노드 차례차례로 원소를 추가하면 다음과 같은 모습이 된다.

7번 노드를 추가하자, 3,4,5,6 리프 노드 중에 가장 먼저 오는 것이 3번 노드이므로 3번 노드에 원소를 추가하도록 하자

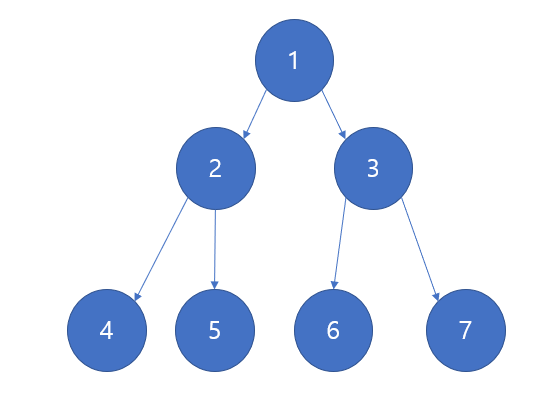
다음으로 8번 노드를 추가한다고 하자, 그럼 4,5,6,7 리프 노드 중에 4번이 먼저 나오므로 4번 노드의 자식으로 추가하도록 하자

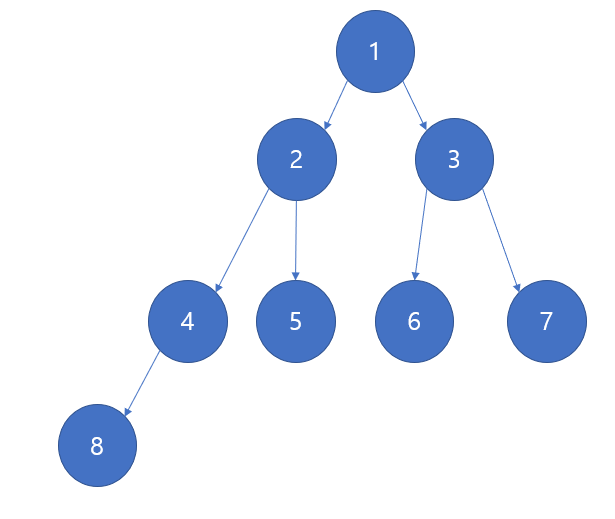
이렇게 된다. 아주 간단하다.
그럼 위에서 말한 수수께기와 같은 단어인 완전 이진 트리는 트리의 높이가 logn을 유지한다는 의미를 해석해보자

이렇게 데이터를 차례대로 쌓으면 데이터가 충분히 퍼지게 된다. 더 분석해보면 점점 트리가 깊어질수록 리프가 많아지므로 데이터를 저장할 공간이 넓어진다는 것이다. 얼마나 넓어지냐면 노드 하나 당 자식을 2개씩 가지므로 2개씩 늘어난다. 그럼 이진 트리에 층층이 늘어나면 2배로 자식이 늘어난다는 것이다. 아래 그림을 보자

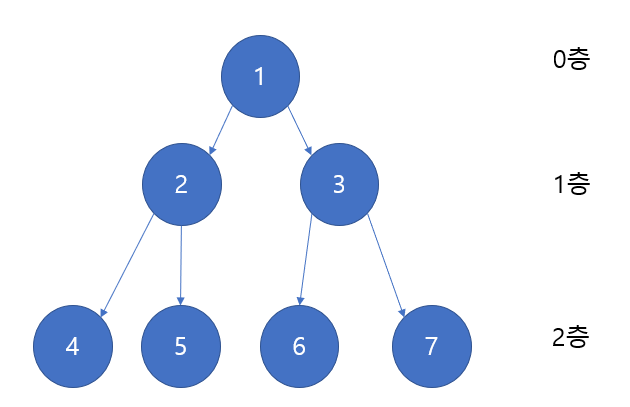
트리는 계층적 구조를 가진다고 했다. 그렇다면 다음과 같이 층을 나눌 수 있다. 0층, 1층 ,2층을 가지는데, 0층은 노드가 1개이다. 그럼 1층은 몇 개일까?? 당연히 2개이다. 0층이 노드가 1개이고 이진 트리는 자식이 left,right 두 개만 존재하므로 1층은 2개의 노드가 있게 된다. 그렇다면 2층은 몇 개 일까?? 1층이 노드가 2개라면, 한 노드 당 자식이 최대 2개 있으므로 2층은 자연스럽게 4개가 된다. 그렇다면 3층은??? 4*2 = 8개가 될 것이다.

그럼 아주 재밌게도, 원소의 개수가 n개라고 하자, n = 2^k 개 라면, k = logn이 되고 k층 전까지를 갖게 될 것이다. 위의 사진은 n =7이지만 대충 8이라고 퉁치자, 이러면 8 = 2^3이므로
3층 전까지인 2층까지를 갖게 된다는 것이다. 그러면 k층 전까지 갖는다는 말은 O(K)라는 말이고, 이는 O(logn)이라는 말이다. 따라서 트리의 높이는 logn이라는 크기를 갖게 된다.

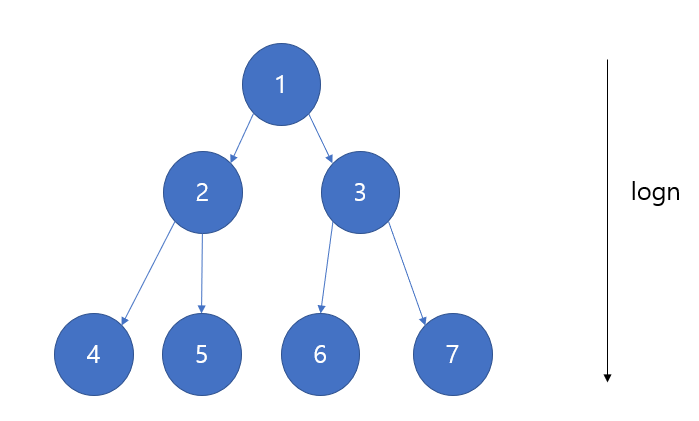
이렇게 트리의 높이가 logn이 된다는 것이다.

완전 이진 트리는 높이가 logn이 됩니다. 왜냐하면 그것은... 야소쿠니까

만약 이해가 안된다면 그냥 이진 트리의 노드들을 최대한 효율적으로 평평하게 담으면 완전 이진 트리가 되고, 완전 이진 트리는 높이가 logn이 된다는 것이다.

이러한 완전 이진 트리의 성질은 꽤나 큰 장점을 갖는다. 트리의 높이가 logn까지 밖에 안된다는 것은 루트에서 리프까지 탐색하는데 logn시간 밖에 걸리지 않는다는 것이다. 이는 n개를 다 탐색해야하는 문제에서 logn번만 탐색하면 되도록 시간을 절약할 수 있어 엄청나게 큰 장점을 얻을 수 있게 된다.

그리고 이러한 완전 이진 트리의 특성을 유지하기 위한 자료구조로 힙과 트라이 등등이 있는데, 우리는 가장 간단하고 구현하기도 쉬운 힙을 배워보도록 하자

3. 힙(heap)

돌고돌아 힙으로 왔다. 트리에 대해 간단하게 알아보겠다고 했으면서, 이게 무슨 서론이냐!!

그만쓰고 싶지만, 그래도 써야한다..

앞서 이야기했듯이 힙은 완전 이진 트리이다.
따라서 다음의 특성을 갖는다.

1. 힙의 각 노드들은 최대 2개의 자식을 갖을 수 있다.
2. 힙은 완전 이진 트리를 유지하기 위해, 노드를 리프의 순서 차례대로 넣는다.

1번은 이진 트리의 특성이다. 2번은 완전 이진 트리를 유지하기 위해서 앞서 노드를 어떻게 추가했는 지 예제를 보면 이해할 수 있다.

그래서 이걸 어떻게 구현하냐구요 ^^???

하지마 그냥 하지마!
보통 트리는 구조체나 클래스로 노드를 구현하고 노드에서 포인터로 자식을 가리키는 로직으로 구현한다. 그러나 힙은 그런 어렵고 상상하기도 싫은 구현과는 거리가 멀 정도로 구현이 간단하다.

얼마나 간단하냐면 배열 하나로 구현이 가능하다.

힙에서 i번째 노드의 왼쪽 자식은 ix2번째 인덱스에 저장하고, 오른쪽 자식은 ix2+1번째 인덱스에 저장하도록 한다. 반대로 자식 k에서 부모로 찾아간다면 부모는 k/2 번째 인덱스에 있다.

정리하자면, 다음과 같다.

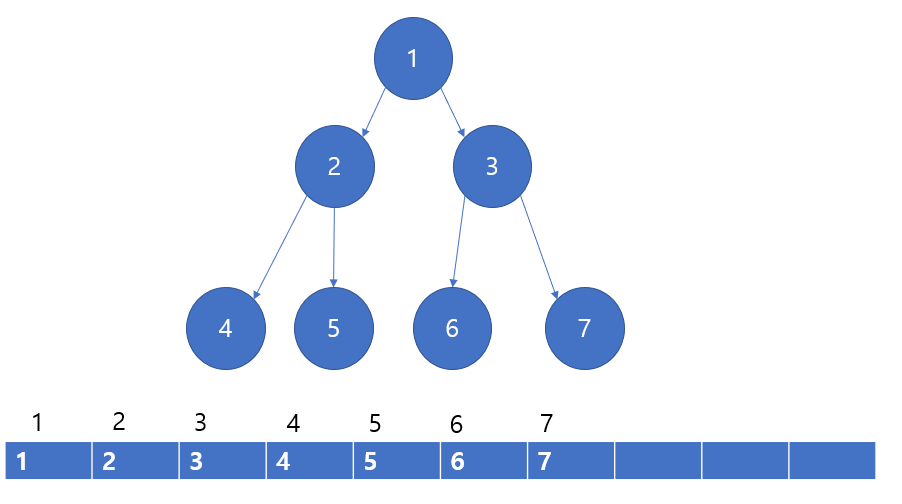
힙이라는 트리의 정보를 관리하기 위해 아래에 배열을 두었다. 인덱스는 1부터 시작한다고 하자,
그럼 노드 1번의 데이터는 루트이므로 1번 인덱스에 저장된다.
1번 노드의 자식은 위의 정의에 따라

left = 1x2 =2
right = 1x2 + 1 = 3
이 된다.

따라서 2번 노드는 인덱스 2번에 저장하고, 3번 노드는 인덱스 3번에 저장한다.
그럼 2번 노드의 자식 4, 5번 노드는 어디에 저장해야할까?? 아주 간단하다.

left = 2x2
right = 2x2+1

이므로 4번 노드는 4번 인덱스로, 5번 노드는 5번 인덱스로 보내버리면 된다.
그럼 여기서 노드 20을 추가해보겠다.

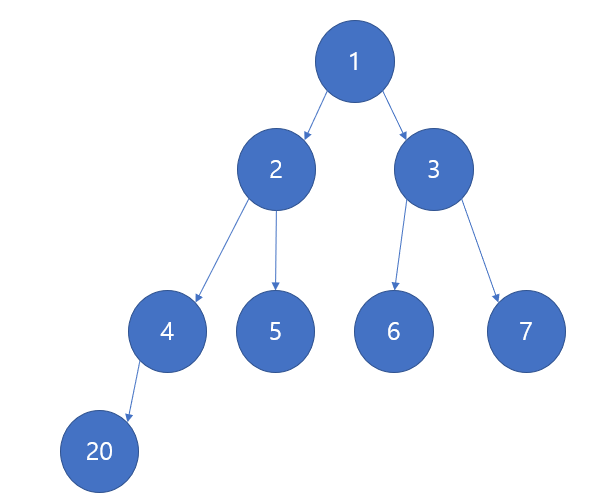
힙은 완전 이진 트리를 유지해야하기 때문에 리프 노드 차례대로 데이터를 저장해야 한다고 했으므로 4번 노드의 왼쪽 자식에 추가된다. 그렇다면 배열에는 어디에 저장해야할까?

4번 노드의 왼족 자식이므로
left = 4x2 = 8
이다. 따라서 8번 인덱스에 노드 20을 저장한다.

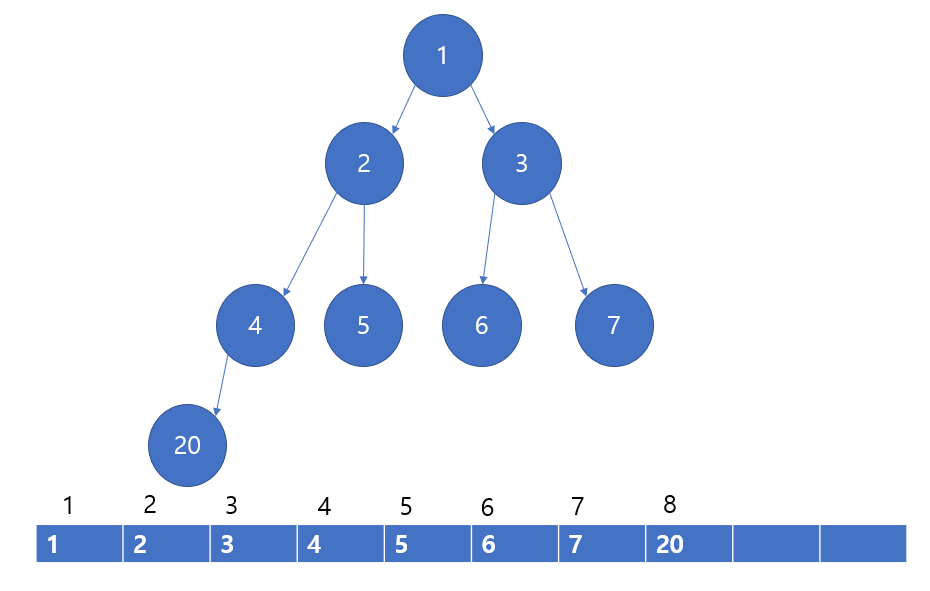
이렇게 된다는 것이다.

이것이 힙의 가장 기본적인 원칙이다.
아주 단순하다 못해, 쉽다.

그러나 힙은 이 자체로는 써먹을 만한 구석이 없다.
별다른 특성이 없기 때문이다. 따라서 우리는 힙의 응용인 최대힙(MaxHeap), 최소힙(MinHeap)을 배워야 한다.

그건 다음 시간에 배우도록 하자~~
최소힙, 최대힙에 들어가면 heapify도 배워야 하고, 이를 응용한 힙정렬까지 배우려면 한 세월이다~~