아뇨 시작하고싶지않습니다. 싫습니다

기수 정렬(Radix Sort)

기수 정렬은 정말 한 번도 문제 풀이에 써본적도, 프로젝트에서 써본 적도 없는 것 같다. 그냥 이런 알고리즘이 있구나 정도만 알고 넘어가도 문제가 없을 것 같다.

계수 정렬과 마찬가지로 O(n) 알고리즘이다. 이제 기수 정렬을 살펴보자

1. 기수 정렬

기수 정렬은 배열에 원소들이 있을 때, 각각의 자리수 별로 정렬하여 완벽히 정렬된 배열을 만들어 내는 알고리즘이다.

기수 정렬의 핵심 아이디어는 각 수들의 n의 자리(n=1~k) 수들을 차례차례 정렬하면 정렬이 된다는 것이다.

들으면 아리송하지만, 예제를 보면 굉장히 단순한 알고리즘이라는 것을 알 수 있다.

다음과 같은 배열이 있다고 하자, 123, 423, 953 ... 637 순서로 나열된 정렬되지 않은 배열이 있을 때, 다음을 어떻게 정렬할 수 있을까??

위의 원리에 대한 정리를 생각해보면 알 수 있다. 배열의 값들을 1의 자리 정렬, 10의 자리 정렬, 100의 자리 정렬을 해보자는 것이다. 그러면 어떻게 될까?? 그리고 왜 100자리가 아닌 1의 자리부터 정렬일까?? 그건 뒤에 알아보도록 하자

먼저 1의 자리부터 정렬해보자, 1의자리를 빨간색으로 표시해두었고, 낮은 수부터 나열해보자는 것이다. 만약 123 , 423의 경우에는 1의 자리가 같은 값이므로 먼저 나온 수를 먼저 나열하도록 하자, 즉, 123이 먼저나왔으니 123을 먼저 둔다.

그렇게 각 수들을 나열하면 1의 자리 배열들 처럼 되어있다. 여기서 끝나지 않고 1의 자리로 정렬된 배열에서 10의 자리로 정렬해보자

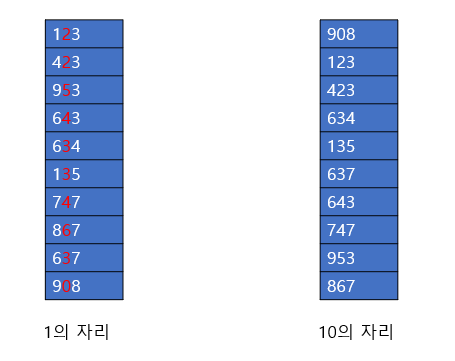
요렇게 1의 자리 배열에서 10의 자리 숫자들을 빨간색으로 표시하였다. 10의 자리로 표시한 부분을 기반으로 낮은 수부터 나열하도록 하자, 나열한 수가 바로 오른쪽 배열이다.

그렇다면 이번에는 10의 자리로 정렬된 배열에서 100의 자리를 기준으로 정렬해보자는 것이다. 100의 자리로 정렬하면 오른쪽과 같은 배열이 나오게 된다.

잘보면 아주 정렬이 이쁘게 되었다는 것을 알 수 있다.

어떻게 이게 가능한 걸까???

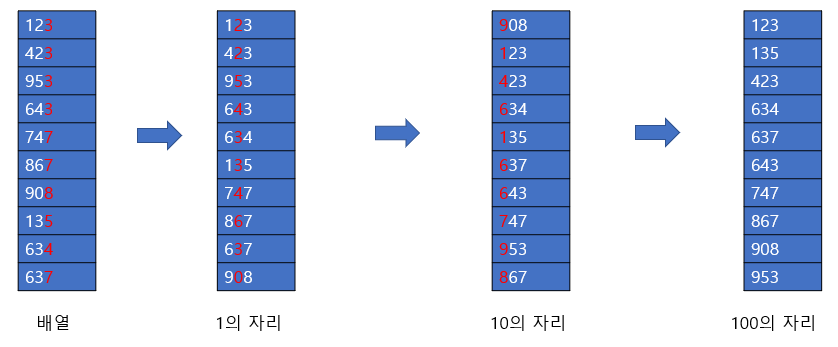
우리가 거친 일련의 과정들이다. 사실 기수 정렬이 왜 되는 지 보다는, 왜 맨 뒤부터 즉, 1의 자리부터 정렬했는데 이게 정렬이 되냐는 사실을 이해하면 기수 정렬의 원리는 모두 이해한 것이다.
왜 뒤부터 정렬해야 정렬이 될까??

아주 단순하다. 만약 100의 자리 수가 똑같은 값들이 있다고 하자, 가령 123, 124이다. 이들을 100의 자리로 비교하기 이전에, 10의 자리를 비교해야한다. 왜냐하면 100의 자리 값이 같기 때문이다. 또한, 10의 자리를 비교하기 이전에 1의 자리를 비교해야한다. 왜냐하면 10의 자리가 같기 때문이다. 따라서 1의 자리를 비교하면 123이 124보다 작다는 것을 알 수 있다.

이후부터는 10의 자리, 100의 자리로 다른 값과 비교하면 된다. 이 처럼 n의 자리가 같은 값이 있을 때 뒤부터(n 다음 값들) 정렬해야 원래 순서를 유지할 수 있는 것이다. 이는 앞의 수가 같은 값들을 분류하기 위함인 것이다. 어차피 앞의 값이 다른 애들, 가령, 223,123은 앞의 자리에서 정렬이 갈리기 때문에 뒤를 비교하는게 무의미하지만, 앞의 자리가 같은 숫자들은 뒤의 자리에 의존할 수 밖에 없다. 따라서, 뒤의 자리 수 부터 정렬하는 것이다.

이것이 기수 정렬이다.

2. 코드

그런데, 생각보다 코드 구현이 만만치 않다.
특히, 일의 자리, 10의 자리, 100의 자리 , .. n 의 자리 끼리의 정렬을 어떻게 하냐는 것이다.

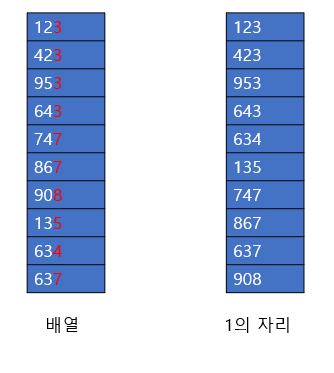
여기서 1의 자리로 정렬하였다. 그럼 정렬 알고리즘으로 무엇을 쓰냐는 것이냐다. 만약 쿽소트, 병합 정렬을 사용하면 분명 O(nlogn)일 텐데, 그럼 기수 정렬은 O(n)이 성립하지 않는다.

그래서 우린 앞서배운 count sort(계수 정렬)을 사용한다. 즉, 기수 정렬을 사용하기 위해서 계수 정렬을 이용해야한다는 것이다. 어차피 자리 수 정렬에서 나오는 숫자들은 0~9이기 때문에 계수 정렬을 사용하기 딱 적절하다. 문제는 구현하기 귀찮을 뿐이다. 코드를 보도록 하자

#include <iostream>
#include <cmath>
//기수정렬
using namespace std;

int n = 10;
int data[] = {123,423,953,643,747,867,908,135,634,637};
int cnt[201];
int ans[201];

void countingSort(int digit){
	int t1 = (int) pow(10,digit);
	int t2 = t1 * 10;
	//초기화
	for(int i = 0; i <= 200; i++) cnt[i] = 0;
	for(int i = 0; i < n; i++){
		int index = (data[i] % t2)/t1;
		cnt[index]++;
	}
	for(int i = 1; i<= 200; i++){
		cnt[i] += cnt[i-1];
	}
	for(int i = n-1; i >= 0; i--){
		int target = (data[i] % t2) / t1;
		int index = --cnt[target];
		ans[index] = data[i];
	}
}

void radixSort(){
	int D = 0;
	int target = data[0];
	while(target != 0){
		target /= 10;
		D++;
	}
	for(int i = 0; i < D; i++){
		countingSort(i);
		for(int j = 0; j < n; j++){
			data[j] = ans[j];
		}
	}
}

int main(){
	radixSort();
	for(int i = 0; i < n; i++){
		cout << ans[i] << ' ';
	}
}

생각보다 까다롭다. 특히 계수 정렬에서 이 부분 생각하는게 많이 귀찮은데

int index = (data[i] % t2)/t1;

1의 자리 값이나, 10의 자리 값이나, 100의 자리 값을 쏙 골라내는 로직이다. 생각보다 막상 만드려고하면 막히기 쉬운 부분이니 잘 알아보자.

이로서 정렬 알고리즘을 모두 마쳤다. 물론 위상 정렬이나 다른 것도 있지만, 그것들은 추후 뒤에서 알아야할 내용들이 많으므로 나중에 배우도록 하자, 다음 알고리즘은 문자열과 트리 쪽과 관련된 부분을 배우도록 하자 이상 끝!