그래프
광기의 비트코인 그래프 떡상가즈아아아아
이번 시간부터는 그래프에 대해서 알아볼 것이다. 지난 번에 힙정렬을 공부하면서 잠깐 트리를 공부하였는데, 트리는 계층이 있었다면 그래프는 계층이 없는 트리라고 생각하면 된다.
정렬 문제들이 면접에서 기본적으로 물어보는 알고리즘이라면, 그래프는 코딩 테스트에서 단골로 등장하는 자료구조이다. 관련 알고리즘이 굉장히 중요하기 때문에 잘 배워두록하자
그럼 각설하고 그래프에 대해서 알아보도록 하자
1. 그래프 기본 용어
그래프는 노드(또는 정점, vertex)와 이들을 잇는간선(edge)으로 구성되어있다.
다음의 그래프를 보자
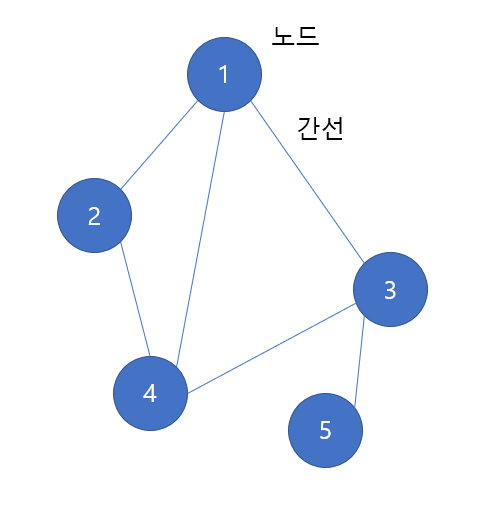
다음의 그래프는 5개의 노드와 6개의 간선으로 이루어진 그래프이다. 보통 노드에는 번호를 붙여 표현하므로, 위와 같이 숫자를 붙여주었다.
-
경로는 한 노드에서 그래프의 간선을 지나 다른 노드까지 가는 길을 의미한다. 경로의 길이는 경로에 포함된 간선의 개수이다. 만약, 위의 예제에서 1번 노드에서 5번 노드로 간다고 하면, 여러 경로 중에서 1-3-5 경로가 가장 짧은 경로가 될 것이다.
-
사이클(cycle)은 처음 노드와 마지막 노드가 같은 경로를 의미한다. 가령 위의 예제에서는 1->4->2->1로 가는 경로와 같은 경우를 사이클이라고 한다.
-
연결 그래프(connected graph)란 그래프의 모든 노드 간에 경로가 존재하는 경우를 말한다. 위의 예제는 모든 노드들이 서로에게 가는 경로가 존재한다. 따라서 연결 그래프라고 말할 수 있다.
그러나 다음의 경우에는 연결 그래프라고 할 수 없다.
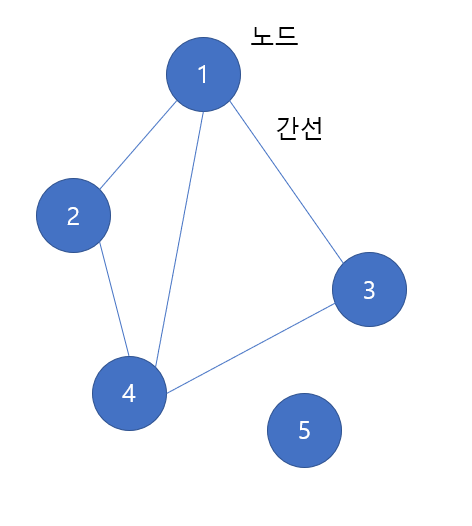
왜냐하면 그 어떤 노드도 5번 노드로 갈 수 있는 경로가 없기 때문이다. 따라서 이는 연결 그래프가 아니다.
-
컴포넌트는 그래프의 연결된 부분을 의미한다. 위의 예제에서는 1,2,3,5 번 노드가 연결된 컴포넌트와 5번 노드 하나 뿐인 컴포넌트 이렇게 2개의 컴포넌트로 이루어진 것이다.
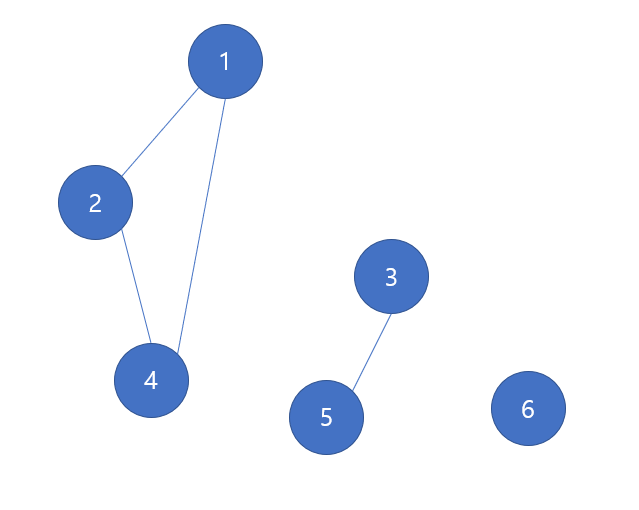
만약 다음의 경우에는 1,2,4번이 하나의 컴포넌트, 3,5가 하나의 컴포넌트, 6이 하나의 컴포넌트이므로 총 3개의 컴포넌트로 이루어졌다고 볼 수 있다. -
트리는 아주 단순하게 말해서 사이클이 없는 연결 그래프를 말한다. 이를 어렵게 말하면, 종속적 의존 관계가 있다고 한다. 종속적 의존 관계는 간단히 계층적 관계가 있다고 생각하면 된다.
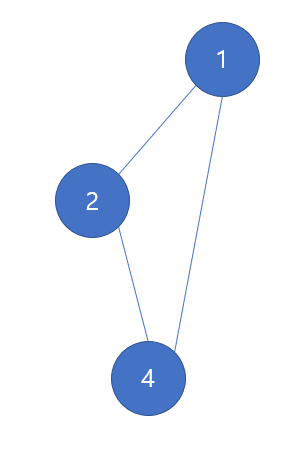
위의 예제는 트리가 될 수 없다. 왜냐하면 사이클이 생기기 때문이다.
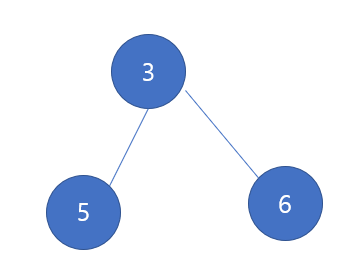
다음의 예제는 사이클이 없으므로 트리라고 볼 수 있다.
따라서, 트리는 그래프의 일종이며, 트리는 사이클이 없는 그래프라고 생각하면 된다.
- 방향 그래프는 간선에 방향이 주어져, 한 방향으로만 이동할 수 있는 그래프이다.
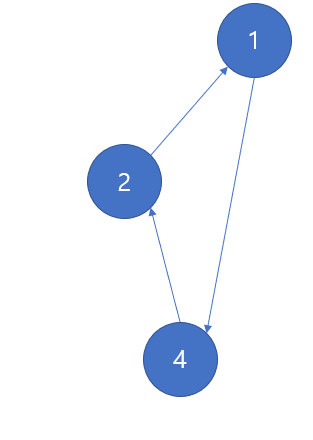
다음의 경우에는 간선을 잘보면 화살표로 표시됨을 알 수 있다. 화살표로 표시된 간선은 방향이 존재하기 때문에 해당 방향이 아니면 다음 노드로 이동할 수 없다. 가령 1에서 4로 가는 간선이 있으므로 1->4 경로는 가능하지만, 4->1은 불가능하다. 4에서 1로 가기위해서는 4->2->1이 유일하다.
만약 간선에 방향이 없다면 양방향 그래프이다. 즉, 간선이 연결된 노드에서는 양쪽다 갈 수 있다는 것이다.
-
가중 그래프는 간선마다 가중치가 존재하는 그래프이다. 대부분의 경우 간선의 가중치가 길이라고 해석되며, 경로의 길이는 간선 가중치의 합이 된다.
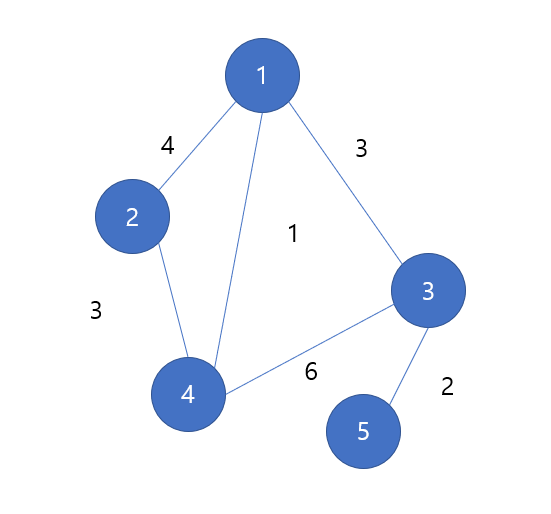
다음과 같이 간선마다 가중치가 할당되어 있는 그래프를 가중치 그래프라 한다. 만약 1->3->5의 경로가 있다고 하자, 그러면 경로의 길이는 어떻게 되는가?? 1->3으로 가는 간선의 가중치가 3이고, 3->5의 가중치가 2이므로 3+2 = 5이다. 추후에 이러한 가중치 그래프에서 어떻게 하면 최소 비용으로 출발지에서 목적지로 도착할 수 있는 지 알고리즘을 배울 것이다. -
이웃한 노드, 인접한 노드는 두 노드가 하나의 간선을 두고 연결되어 있는 경우를 말한다. 위의 예제에서 1번 노드의 경우, 2 , 3, 4번 노드가 1개의 간선을 두고 연결되어 있음을 알 수 있다. 따라서, 1번의 이웃한 노드(인접한 노드)는 2 , 3, 4번 노드이다. 또한, 이웃한 노드의 개수를 차수라고 부른다. 따라서, 1번 노드의 차수는 3개이다.
-
정규 그래프는 모든 노드의 차수가 같은 경우를 말한다. 즉, 한 노드의 차수가 상수 d라면 모든 노드의 차수는 상수 d여야 한다는 것이다.
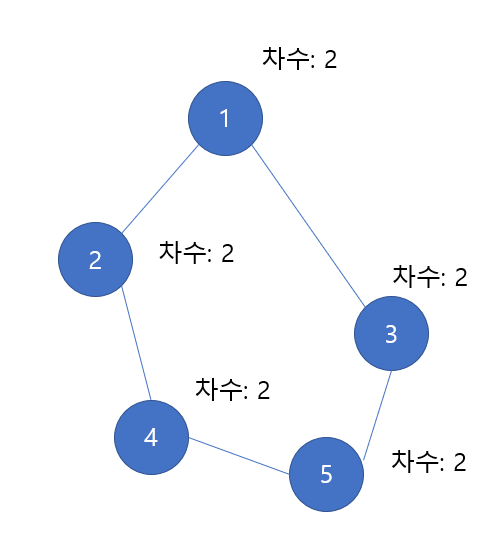
다음의 그림을 보자, 모두 각 차수가 2로 이어져 있다. 따라서 정규 그래프라고 할 수 있다.
한 가지 번외로, 만약 그래프의 전체 간선이 m개 라면, 전체 차수의 수는 2m이다. 간선 하나가 두 노드에 이어지기 때문에 전체 차수는 2씩 늘어날 수 밖에 없다. 따라서 차수는 2m이 된다.
- 완전 그래프는 노드의 개수가 n개 이고, 모든 노드의 차수가 n-1인 경우, 즉 모든 노드 간에 간선이 있는 경우를 의미한다. 경로 상으로 단 하나의 간선을 거치면 한 노드에서 모든 노드로 갈 수 있다는 의미이다.
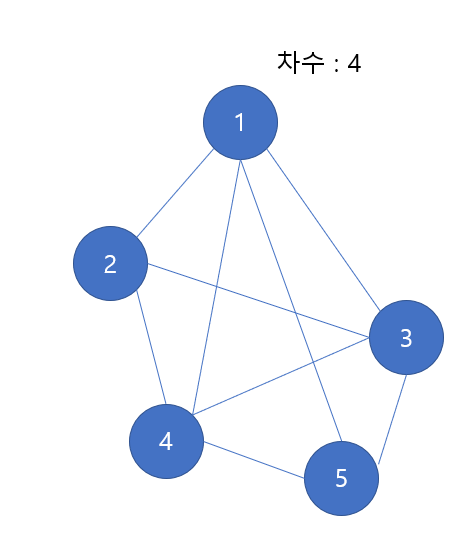
다음의 그래프는 노드의 개수가 5개 인데, 모든 노드의 차수가 4이다. 이는 한 노드에서 모든 노드로 이어져 있다는 것을 의미하므로, 완전 그래프라고 할 수 있다.
- 진입 차수는 방향 그래픝에서 해당 노드로 향하는 간선의 개수이다. 진출 차수는 그 노드에서 시작하는 간선의 개수이다.
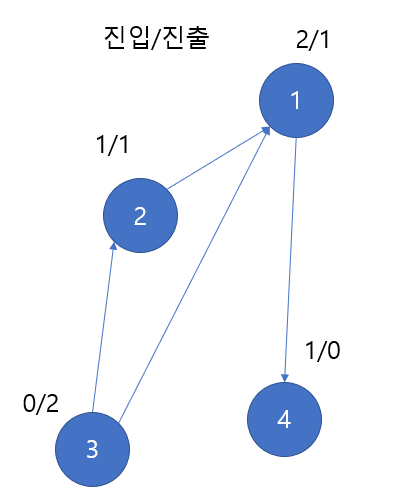
다음의 사진을 보자, 1번 노드로 2, 3번 노드가 향하고 있다. 따라서 1번 노드의 진입 차수는 2가 된다. 1번 노드는 4번 노드를 향해가기 때문에 진출 차수는 1이다. 3번 노드의 경우에는 3번 노드로 가는 진입 차수가 0이고, 1번 , 2번 노드로 가기 때문에 진출 차수가 2이다.
- 이분 그래프은 모든 노드를 두 가지 색깔 중 하나로 칠하되, 이웃 노드의 색깔이 같은 경우가 없도록 만드는 것이다.
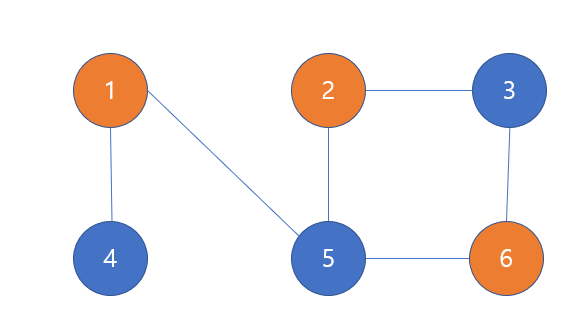
다음의 그래프를 보면, 노드가 주황색, 파란색 하나로 결정이 된다. 그러나 이웃한 노드끼리는 색이 달라야 하므로 다음과 같은 모습이 나온다. 이웃한 노드끼리 색이 다르다면 홀수 개의 간선으로 이루어진 사이클이 없는 경우와 일치한다.

뭐 이렇게 외울게 많은가, 뇌가 뽑힐 것 같다. 그냥 이런게 있구나 싶은 마음으로 넘어가면 된다. 점차 배우면서 외우면 되니까 말이다.
2. 그래프 표현 - 인접 리스트(stl)
그래프를 표현하는 대표적인 방법으로는 인접 리스트와 배열이 있다. 그러나, 배열로 표현하는 방법은 메모리 효율이 굉장히 떨이지기 때문에 인접 리스트로 구현하는 방법을 같이 배워보자
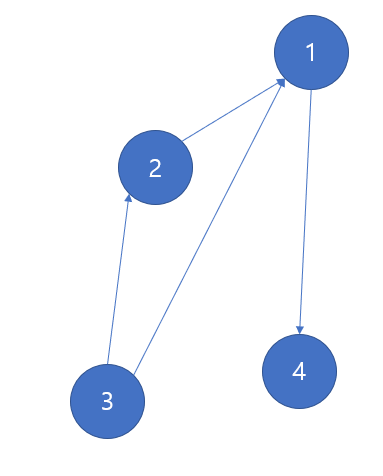
다음의 방향 그래프를 표현해보자
cpp의 stl을 사용하면 매우매우 간단하게 표현이 가능한데
vector<int> graph[MAX_NODE_SIZE];이게 graph 자료구조의 끝이다. 노드의 최대 개수가 N개 라면, graph[N]이 되는 것이다. N개의 벡터를 만드는 것인데, 인덱스는 노드의 번호를 의미한다. 즉, graph[1] 은 노드 1을 의미하는 것이다. 또한, vector에 저장할 값은 해당 인덱스(노드)에서 이웃한 노드로 갈 수 있는 간선을 저장하는 것이다.
따라서, graph[1].push_back(4)가 의미하는 바는 1번 노드와 이웃한 4번 노드로 가는 간선이 존재한다는 것이다. 만약 2번 노드에서 이웃한 노드 중에 1번 노드로 가는 간선이 존재한다면, graph[2].push_back(1) 로 써준다. 한 개의 노드 당 간선의 수는 유동적이므로 vector로 표현하는 것이다.
#include <iostream>
#include <vector>
#define MAX_NODE_SIZE 10
using namespace std;
vector<int> graph[MAX_NODE_SIZE];
int main(){
graph[1].push_back(4);
graph[2].push_back(1);
graph[3].push_back(1);
graph[3].push_back(2);
for(int i = 1; i <= MAX_NODE_SIZE; i++){
cout << "NODE " << i << ' ';
for(int j = 0; j < graph[i].size(); j++){
cout << graph[i][j] << ' ';
}
cout << '\n';
}
}위의 그림을 표현한 예제이다. 출력하면 다음의 결과가 나온다.
NODE 1 4
NODE 2 1
NODE 3 1 2
NODE 4
NODE 5
NODE 6
NODE 7
NODE 8
NODE 9
NODE 10 NODE 1 4는 노드 1이 이웃한 노드로 4번 노드로 향하는 간선이 있다는 것을 의미한다. NODE 3 1 2는 노드 3번에서 이웃한 노드로 노드 1번, 노드 2번으로 가는 간선이 있다는 것을 의미한다. 위의 코드에서,
graph[i].size()는 i번째 노드에서 진출하는 간선의 개수를 의미한다.
그럼 만약 무방향 그래프인 경우(양방향 그래프)인 경우는 어떻게 해야할까??
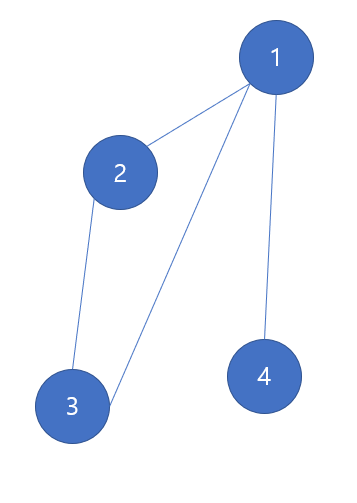
다음과 같은 양방향 그래프가 있다고 한다면 양쪽 모두 갈 수 있다는 것을 의미하므로, 양쪽에 간선을 넣으주면 된다. 즉, 1번 노드에서 이웃한 노드로 4번 노드가 하나의 간선으로 이어져있다. 1번 노드에서 4번 노드로 하나의 간선으로 갈 수 있고, 4번 노드에서 1번 노드로 하나의 간선으로 갈 수 있다.
따라서 다음과 같이 표현한다.
vector graph[N];
graph[1].push_back(4);
graph[4].push_back(1);굉장히 단순하다. 1->4 번으로 갈 수 있고, 4->1 번으로 갈 수 있다면 양쪽 모두에 넣어주면 된다.
#include <iostream>
#include <vector>
#define MAX_NODE_SIZE 10
using namespace std;
vector<int> graph[MAX_NODE_SIZE];
int main(){
graph[1].push_back(4);
graph[4].push_back(1);
graph[1].push_back(2);
graph[2].push_back(1);
graph[1].push_back(3);
graph[3].push_back(1);
graph[2].push_back(3);
graph[3].push_back(2);
for(int i = 1; i <= MAX_NODE_SIZE; i++){
cout << "NODE " << i << ' ';
for(int j = 0; j < graph[i].size(); j++){
cout << graph[i][j] << ' ';
}
cout << '\n';
}
}결과는 다음과 같다.
NODE 1 4 2 3
NODE 2 1 3
NODE 3 1 2
NODE 4 1
NODE 5
NODE 6
NODE 7
NODE 8
NODE 9
NODE 10 NODE 1 4 2 3은 노드 1번에서 하나의 간선을 통해서 4 2 3 노드로 갈 수 있다는 것을 의미한다. 양방향이기 때문에 4번 노드에도 1번 노드로 갈 수 있다는 것이 표현되어야 한다. NODE 4 1을 보면 노드 4번에서 이웃한 노드인 1번으로 갈 수 있다는 것을 확인할 수 있다.
3. 그래프의 표현 - 인접 리스트(쌩구현)
그런데, stl을 쓰면 아주아주 좋고 편하겠지만 그러면 재미가 없다. 또한, 삼성 알고리즘 B형이나, pro 시험을 준비하시는 분이라면 도움이 될 만한 자료가 되었으면 한다.
#include <iostream>
#define MAX_NODE_SIZE 10
using namespace std;
typedef struct Node{
int number;
Node *next;
};
Node pool[MAX_NODE_SIZE + 1];
int pi = 0;
Node* alloc(){
return &pool[pi++];
}
typedef struct Graph{
int size;
Node *next;
Graph(){
size = 0;
next = 0;
}
void push_back(int nodeNumber){
Node *newNode = alloc();
newNode->number = nodeNumber;
newNode->next = next;
next = newNode;
size++;
}
};
Graph graph[MAX_NODE_SIZE + 1];
int main(){
graph[1].push_back(4);
graph[1].push_back(2);
graph[1].push_back(3);
graph[2].push_back(1);
graph[2].push_back(3);
graph[3].push_back(1);
graph[3].push_back(2);
graph[4].push_back(1);
for(int i = 1; i <= MAX_NODE_SIZE; i++){
Node *cur = graph[i].next;
cout << "NODE " << i << " : ";
for(int j = 0; j < graph[i].size; j++){
cout << cur->number << ' ';
cur = cur->next;
}
cout << '\n';
}
}코드를 설명해보자
typedef struct Node{
int number;
Node *next;
};
먼저 Node 구조체를 선언한다. 현재 예제는 별로 특별한 정보가 없으므로 노드의 번호를 담아두기로 하자, 또한, 노드에 *next 포인터를 두어 다음 노드를 가리키도록 한다. 하나의 링크드 리스트를 표현한 것으로 생각하면 된다.
typedef struct Graph{
int size;
Node *next;
Graph(){
size = 0;
next = 0;
}
void push_back(int nodeNumber){
Node *newNode = alloc();
newNode->number = nodeNumber;
newNode->next = next;
next = newNode;
size++;
}
};다음은 graph이다. 위에서 vector와 비슷한 자료구조로 생각하면 된다. vector처럼 유동적으로 값을 저장해야 하므로 링크드 리스트를 사용하였고, next 포인터가 이와 관련된 데이터들의 주소 값을 이어 붙여 저장하도록 하였다.
push_back 연산을 통해 링크드 리스트의 헤드 앞에 새로운 node가 추가되도록 하였다.
그럼 각 graph에서 링크드 리스트 노드가 표현하는 바는 무엇일까??
Graph graph[MAX_NODE_SIZE + 1];바로 graph[]에서 i 번째 노드(인덱스)에 연결된 간선들을 표현하는 것이다. 즉, i번째 인덱스와 이웃한 노드들을 next 포인터 엮어 링크드 리스트를 만든 것이다.
int main(){
graph[1].push_back(4);
graph[1].push_back(2);
graph[1].push_back(3);
graph[2].push_back(1);
graph[2].push_back(3);
graph[3].push_back(1);
graph[3].push_back(2);
graph[4].push_back(1);
for(int i = 1; i <= MAX_NODE_SIZE; i++){
Node *cur = graph[i].next;
cout << "NODE " << i << " : ";
for(int j = 0; j < graph[i].size; j++){
cout << cur->number << ' ';
cur = cur->next;
}
cout << '\n';
}
}나머지 연산들은 별로 특별한 것은 없다. 위에서 구현한 자료구조를 이용하여 입력, 출력해준 것 뿐이다.
물론 코딩 테스트에서 이렇게 구현할 필요는 없다. 쓸데없는 시간 낭비이다. 코딩 테스트에서는 stl을 사용하여 구현하도록하고, 면접이나 현업에서 stl에 없는 기능이 필요할 때 만들어보도록 하자
