
신입들이 싫어합니다
프로그래머로서 취업을 하려면 코딩 테스트롤 통과해야한다. 물론 코딩테스트가 없는 회사도 있지만, 굳이 코딩테스트를 포기하여 다양한 회사의 선택지를 줄일 필요는 없다. 물론, 코딩테스트를 통과한다해서 끝인 것은 아니다.
흔히 말하는 공룡 IT기업들이 원하는 현실이라고 생각하면 된다. 물론 예외도 있겠지만, 내 친구들, 동기들, 선배들은 모두 경력이 있는데 신입으로 지원하던지 또는 이게 신입이냐? 소리나오는 실력을 가진 친구들이었다.
각설하고, 그래서 코딩테스트를 준비하려면 무슨 알고리즘을 열심히 공부해야하냐?? 라고 한다면, 아주아주 단골 소재 알고리즘인 그래프의 순회 알고리즘인 BFS, DFS이다. 오늘은 DFS에 대해서 먼저 알아보도록 하자
특히 S전자에서 이 알고리즘을 자주 냈었기 때문에 필수적으로 알아야만하는 알고리즘이다. 필자도 S전자 준비과정에서 이 알고리즘 관련 문제만 100~200정도 푼 것 같다. 내일도 이 회사에 출근해야한다
S전자 이외에도 여러 회사에서 단골로 등장하는 알고리즘이니까 꼭 공부해보도록 하자
1. DFS(Depth First Search)
이전 시간에 그래프가 무엇인지에 대한 기본적인 용어와 배경을 알아보았다. 그러면 그래프를 어떻게 탐색(순회)할 수 있을까??
그래프의 순회라는 것은 시작 노드에서부터 출발하여 그래프의 간선을 따라 이동해 가며 도달 가능한 모든 노드를 처리하는 것이다. 즉, 그래프의 모든 노드를 방문하는 알고리즘이라는 것이다.
따라서, 자연스럽게 방문해야할 노드가 N개 이고 간선의 개수가 M개이면 모든 노드를 방문해야하므로 시간복잡도는 O(N+M)이 된다. 그래서 2차원 배열로 가로 세로가 N, M 이면 시간 복잡도가 O(NM)이 된다.
대표적인 두 가지 알고리즘이 있는데, 하나는 깊이 우선 탐색(DFS)이고, 하나는 넓이 우선 탐색(BFS)이다. 먼저 DFS에 대해서 알아보도록 하자
- 깊이 우선 탐색(DFS)
깊이 우선 탐색은 새로운 노드가 발견되는 동안 단일한 경로를 따른다. 그 다음에는 방문했던 이전 노드로 돌아가 그래프의 다른 부분을 탐색하기 시작한다. 진행하는 과정에서 방문했던 노드를 기록하므로, 각 노드는 한 번씩만 처리된다.
책에서 발췌한 내용인데, 내가 들어도 뭔말인지 잘 모르겠다. 간단히 정리하자면, 한 노드로 부터 시작하여, 연결된 간선을 따라 쭉 노드들을 방문하고, 막다른 길이 나오면, 뒤로 가서 더 방문할 노드가 있는 지 검사한다는 것이다.
예제를 보면서 이해해보자
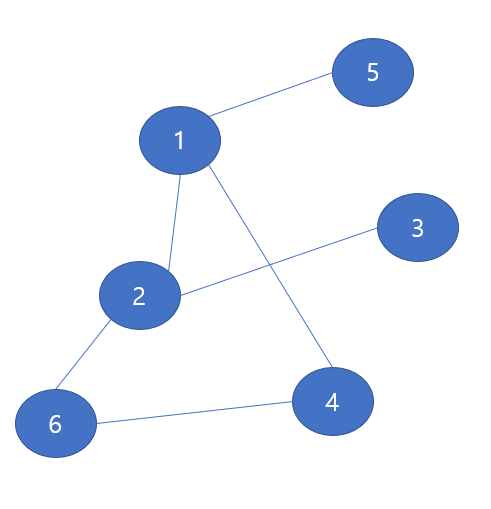
다음의 그래프가 있다고 하자, 우리는 DFS 알고리즘을 통해, 모든 노드를 방문 해볼 것이다.
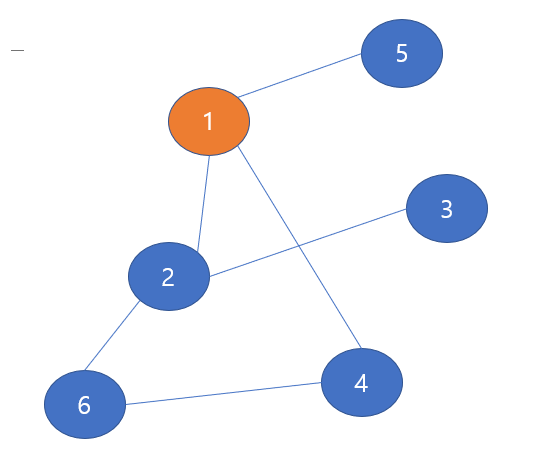
시작 노드를 1번 노드로 결정했는데, 이는 문제에 따라 다를 수 있다. 현재에서는 임의로 아무 노드를 시작 노드로 두어도 문제가 되지 않으므로 1번 노드를 선택했다. 주황색으로 표시한 것은 방문했다는 check이다.
이제 1번 노드와 이웃한 노드들을 살펴보자,
1번 노드와 이웃한 노드 : 2, 5
다음 순회할 노드로 2번 노드를 선택해보자, 5번 노드를 선택해도 상관없다.
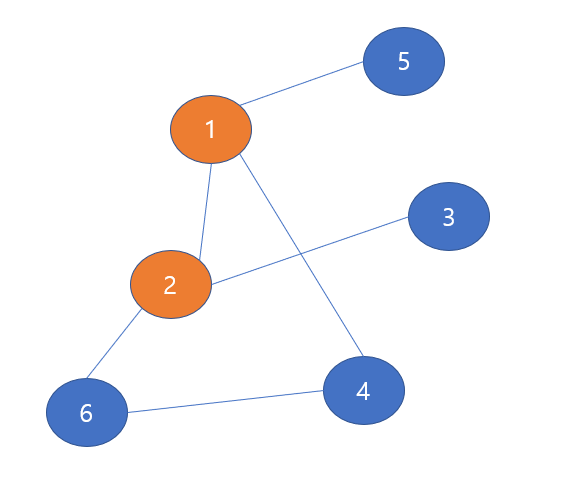
이렇게 될 것이다. 2번 노드가 선택되었고, 방문했다는 표시로 check를 해주자.
2번 노드와 이웃한 노드들을 살펴보면,
2번 노드와 이웃한 노드 : 1, 6, 3
여기서, 1번 노드는 이미 주황색으로 check가 되어있는 상황이므로 방문할 필요가 없다.
그렇다면 남은 이웃한 노드 중에 6번 노드를 선택해보자, (3번 노드를 선택해도 상관이 없다)
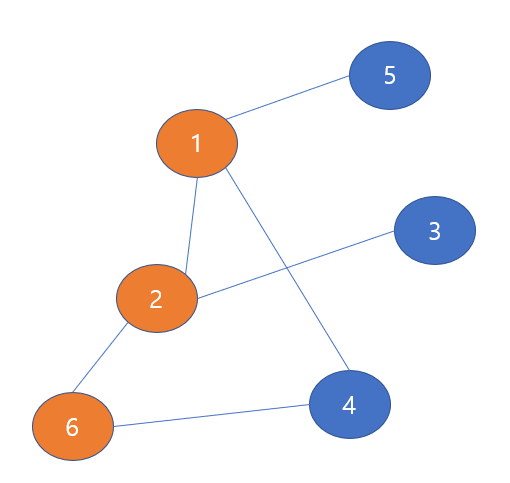
6번 노드를 방문하고 check해주면 다음과 같은 그림이 된다.
이번에도 현재 노드(6번 노드)와 이웃한 노드들을 살펴보자
6번 노드와 이웃한 노드 : 2 , 4
2번 노드는 주황색으로 check되어 있으므로 이미 방문했다는 것을 나타낸다. 따라서 우리가 방문할 수 있는 노드는 4번 노드 밖에 없다.
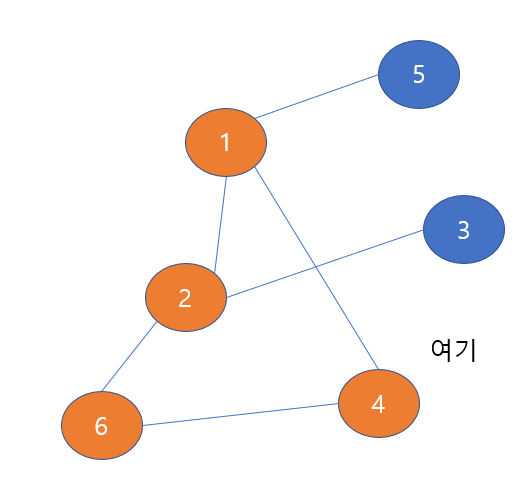
4번 노드를 방문해주고 주황색으로 check해준다.
이제 4번 노드가 이웃한 노드를 살펴보자
4번 노드와 이웃한 노드 : 6, 1
6번 노드와 1번 노드 모두 주황색으로 check되어있으므로 방문할 필요가 없다. 따라서, 4번 노드에서 더 이상 방문할 노드가 없다.
여기서부터가 굉장히 중요하다. 어떻게 해야할까??
위에서 DFS의 원리를 살펴보았다. 그 의미를 리마인드 해보자
- 깊이 우선 탐색(DFS)
깊이 우선 탐색은 새로운 노드가 발견되는 동안 단일한 경로를 따른다. 그 다음에는 방문했던 이전 노드로 돌아가 그래프의 다른 부분을 탐색하기 시작한다. 진행하는 과정에서 방문했던 노드를 기록하므로, 각 노드는 한 번씩만 처리된다.
여기서 다음의 의미를 되새겨보자
'새로운 노드가 발견되는 동안은 단일한 경로를 따른다'
우리는 1->2->6->4 로 탐색하였는데, 이는 모두 이전에 방문한 적 없는 새로운 노드들이었다. 이렇게 만들어진 경로는 새로운 노드를 발견하는 동안 만들어진 것이다.
그런데, 4번 노드 이후로는 새로운 노드가 없다. 이때에는 어떻게 해야할까?
그 다음에는 방문했던 이전 노드로 돌아가 그래프의 다른 부분을 탐색하기 시작한다.
4번 노드 이후로는 새로운 노드가 없으므로 이전 노드로 돌아가 새로운 노드가 있는 지 없는 지 탐색하라는 것이다. 즉, 4번 노드의 이전 노드인 6번 노드로 돌아가라는 것이다.
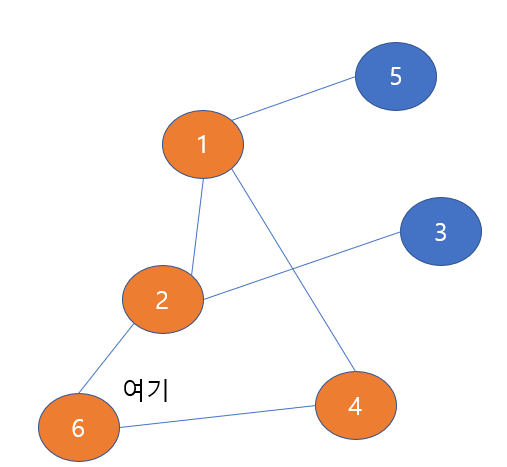
위 그림에서 '여기'로 표시한 것이 바로 현재 노드이다. 현재 노드로 6번 노드로 되돌아 왔는데, 6번 노드와 이웃한 노드 중에서 방문하지 않은 노드들이 있는 지 확인해보자
없다!
그러므로 6번 노드의 이전 노드로 되돌아가보도록 하자
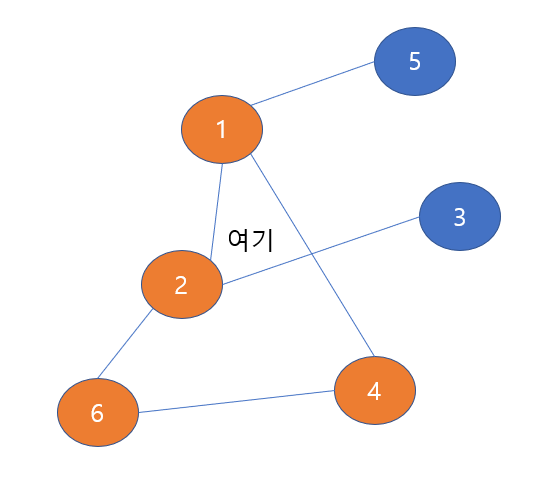
바로 2번 노드가 된다. '여기'로 표시해두었다.
2번 노드와 이웃한 노드들 중에서 방문한 노드가 아닌 노드를 보면 3번 노드가 있다.
따라서 우리는 3번 노드로 방문한다.
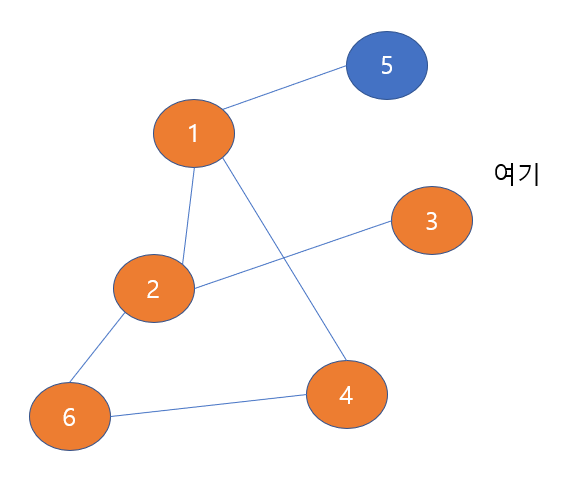
3번 노드를 방문하였으므로 우리는 3번 노드에 주황색으로 check해준다.
3번 노드와 이웃한 노드 중에서 방문하지 않은 노드를 살펴보자,

현재 이분은 존잘이되었다고 한다
없다! 따라서, 우리는 이전 노드인 2번 노드로 다시 돌아간다.
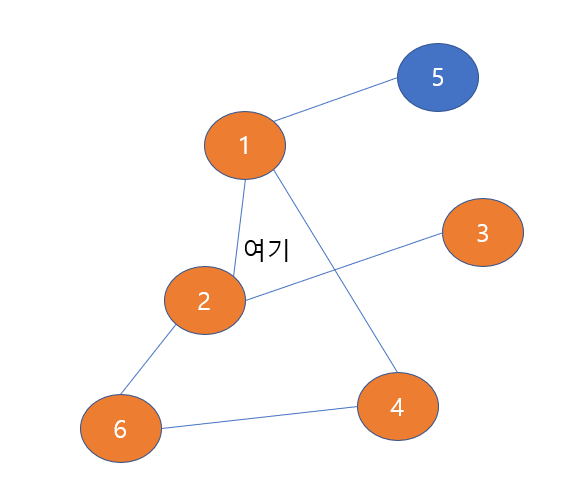
다시 2번 노드로 되돌아오면 2번 노드와 이웃한 노드 중에서 방문한 적 없는 노드는 없다는 것을 알게된다.
따라서 2번 노드에서도 다시 이전 노드인 1번 노드로 되돌아온다.
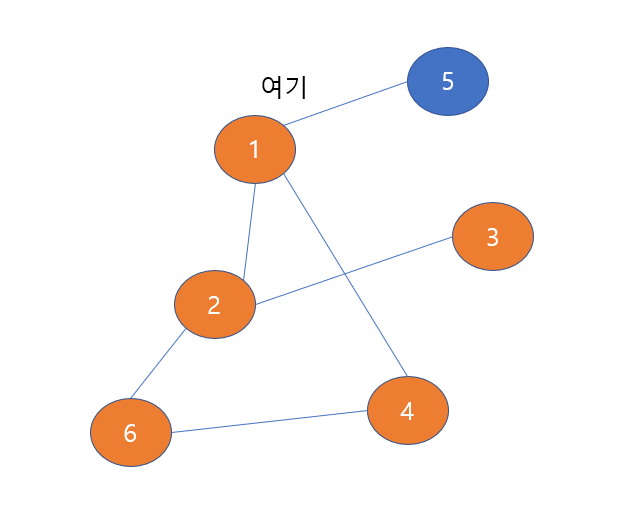
1번 노드에서 이웃한 노드 중에서 방문한 적 없는 노드가 있는가??
있다!! 바로 5번 노드이다. 따라서 우리는 5번 노드를 방문해보도록 하자
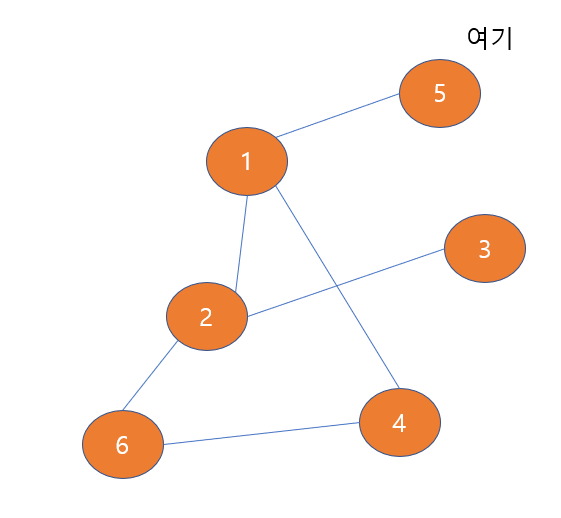
5번 노드를 방문했다고 주황색으로 check해주자,
이제 5번 노드와 이웃한 노드 중에서 방문한 적이 없는 노드가 있는 지 확인해보자,
없다!!
그럼 이전 노드인 1번 노드로 되돌아오지만, 1번 노드 역시도 이웃한 노드 중에서 방문 안 한 노드가 없기때문에 DFS 알고리즘이 끝나게 된다.
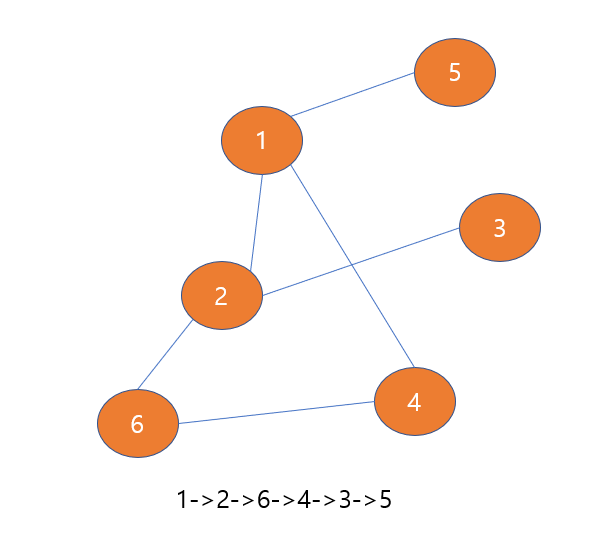
그래프 아래에 표시해둔 경로는 우리가 방문한 적 없는 노드들을 방문한 경로이다.
우리는 1->2->6->4->3->5 순서로 방문하였고, 이는 모든 노드를 방문한 것이다.
이것이 DFS 알고리즘이고 그렇게 어려울 것이 없다.
다시 원리 부분을 리마인드해보자
- 깊이 우선 탐색(DFS)
깊이 우선 탐색은 새로운 노드가 발견되는 동안 단일한 경로를 따른다. 그 다음에는 방문했던 이전 노드로 돌아가 그래프의 다른 부분을 탐색하기 시작한다. 진행하는 과정에서 방문했던 노드를 기록하므로, 각 노드는 한 번씩만 처리된다.
조금 이제는 이해가 되는 것 같은가??
간단하게 말해서, 한 노드에서 시작해서 쭉 연결된 간선을 타고 찔러들어간다. 여기서 노드를 방문했다면 방문했다는 표시를 해주고, 이제 더 이상 새로운 노드가 없다면, 방문했던 이전 노드로 되돌아가서 새로운 노드로 쭉 질러들어가는 것이다.
쭉 질러들어간다는 것이 바로 이런 것이다.
1->2->6->4
1->2->3
1->5
이렇게 새로운 노드를 발견하고, 막 다른 길에 다다를 때 까지의 경로를 말한다. 이것이 '깊이 우선 탐색'으로 불리는 이유이다. 한 노드로부터 시작하여 막다른 길이 나올 때까지 관통하는, 즉 한 노드의 깊이를 모두 체크해보는 것이다.
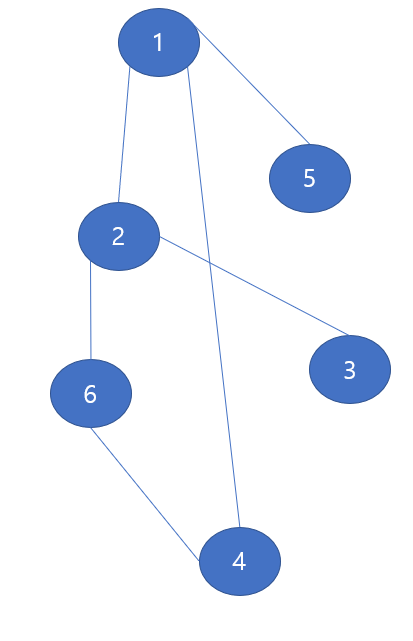
위의 그림은 이전 예제의 그래프를 마치 트리같이 길게 늘려놓은 것 일 뿐이다. '깊이'라는 의미를 쉽게 이해하기위해 다음 처럼 노드를 배치하였다.
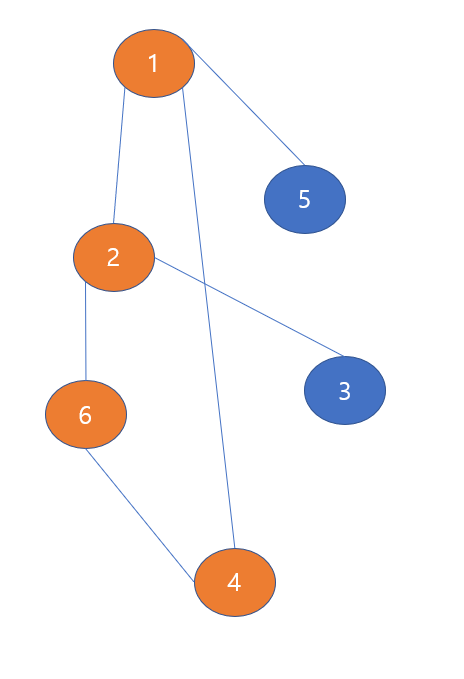
다음의 그림을 보면 1->2->6->4 경로를 방문하여 막다른 길에 간 것을 확인할 수 있다. DFS는 깊이 우선 탐색으로 시작 노드인 1번 노드가 찔러 들어갈 수 있는 만큼 쭉 찔러들어가고 이는 곧 깊이가 된다. 위의 예제는 깊이 4인 것을 보여준다.
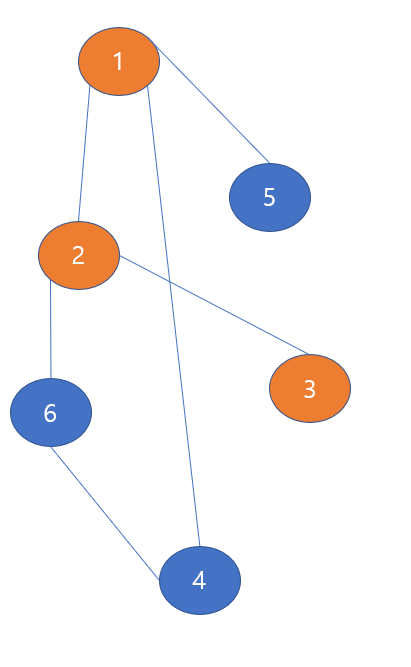
다음은 1->2->3으로 막다른 길이 나왔을 때의 경로이다. (6,4번 노드는 이미 방문했었지만 그냥 보기 편하게 1 2 3번 노드만 주황색으로 표시하였다.)
1번 노드에서 깊게 쭉 찔러들어간 것으로 1->2->3 경로를 만들게 된다.
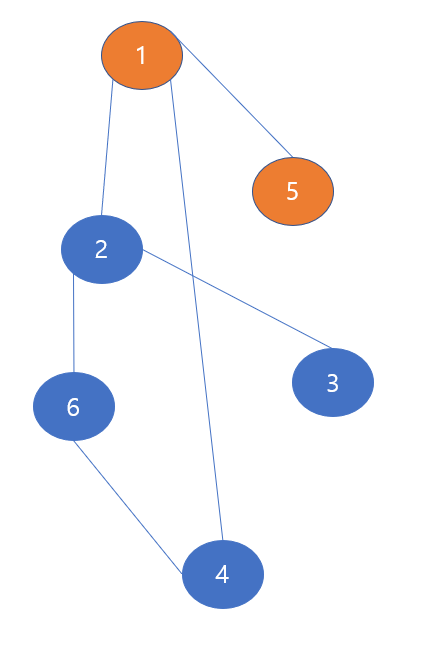
마지막으로 1->5 경로이다. 위의 사진들은 모두 1번 노드가 깊이 중심으로 쭉 찔러들어가서 방문했을 때, 막다른 길에 봉착하면 생기는 경로로 DFS 알고리즘의 과정을 보여준다.
이것이 DFS이다.
시간 복잡도는 모든 노드를 방문하므로 노드가 N개이면 O(N)일 수 밖에 없다. 여담으로 DFS 미로찾기 즉, 미로에서 출구찾기 알고리즘과 동일하다. 필자 1학년 때의 과제가 c언어로 로봇이 미에서 빠져나오도록 하는 프로그래밍을 하라는 것이었다. 교수님이 알고리즘도 안 알려줘놓고 구현하라고해서 친구들과 머리싸매서 구현을 했던 기억이 아직도 새록새록하다. 그 때 DFS를 몰랐지만 재밌게도 DFS랑 똑같이 구현을 했어서, 조교님의 의심을 받았던 기억이 있다. 좀 알려주고 시키던지
2. DFS 구현 - stl
이전 시간에 graph을 표현하는 방법을 보았다.
stl을 사용하여 graph도 구현하고, DFS도 구현해보려고 한다.
DFS 구현에 필요한 준비물은 다음과 같다.
- graph 자료구조 (stl vector 이용)
- check 배열 ( 방문했는 지 안했는 지 확인을 위함)
다음의 자료구조들이 필요하고, 알고리즘을 정리하면 다음과 같다.
- 현재 노드가 방문한 노드이면 방문하지 않는다.
- 현재 노드가 방문하지 않은 노드이면 방문하도록 하고, check해준다.
- 현재 노드와 이웃한 노드 중에서 방문한 적이 없는 노드를 찾아서 방문해주도록 한다. 여기서 방문은 dfs를 재귀적으로 실행하도록 한다.
이제 끝이다. 위에서 우리가 살펴본 예제를 구현해보도록 하자
#include <iostream>
#include <vector>
#define MAX_NODE_SIZE 10
using namespace std;
vector<int> graph[MAX_NODE_SIZE +1];
bool check[MAX_NODE_SIZE+1];
void dfs(int node){
if(check[node]) return;
check[node] = true;
cout << node << ' ';
for(int i = 0; i <graph[node].size(); i++){
int nextNode = graph[node][i];
dfs(nextNode);
}
}
int main(){
graph[1].push_back(2);
graph[1].push_back(4);
graph[1].push_back(5);
graph[2].push_back(1);
graph[2].push_back(3);
graph[2].push_back(6);
graph[3].push_back(2);
graph[4].push_back(1);
graph[4].push_back(6);
graph[5].push_back(1);
graph[6].push_back(2);
graph[6].push_back(4);
dfs(1);
}아주 간단하다.
graph 표현은 이전 시간에 알아보았기 때문에 넘어가고, 우리는 dfs 함수만을 알아보도록 하자
void dfs(int node){
if(check[node]) return;
check[node] = true;
cout << node << ' ';
for(int i = 0; i <graph[node].size(); i++){
int nextNode = graph[node][i];
dfs(nextNode);
}
}먼저 파라미터로 node를 받는데, 이는 현재 노드에 해당한다. 만약 check[node]가 true이면 방문하였으므로 함수를 종료한다.
만약, 방문한 적 없는 노드이면 check[node] = true로 해주고, node를 출력해준다. 다음으로는 for문을 사용하는데, 이는 저번 시간에 배운 이웃한 노드들을 쭉 순회하는 것이다. 이웃한 노드들을 재귀적으로 dfs를 돌리도록 하자,
만약, 이웃한 노드가 이미 방문한 적이 있다면 바로 check[nextNode]는 true이기 때문에 return되어 함수가 종료되고, 다시 이전 노드의 for문으로 돌아올 것이다. 그리고 for문은 다음 순회로 넘어가서 다음 이웃한 노드를 dfs 순회할 것이다.
만약, 이웃한 노드가 아니라면 새로운 노드이므로, 그 노드를 기준으로 쭉 연결한 노드를 찔러들어갈 것이다.
출력 결과는 다음과 같다.
1 2 3 6 4 5이는 노드를 생성할 때 이웃한 노드 순서로 방문했기 때문에 다음의 순서가 된다.
3. DFS 구현 - stl 없이 구현
사실 stl없이 구현은 graph가 까다로웠지 DFS전혀 어려울 것이 없다.
#include <iostream>
#define MAX_NODE_SIZE 10
using namespace std;
typedef struct Node{
int number;
Node *next;
};
Node pool[MAX_NODE_SIZE + 1];
int pi = 0;
Node* alloc(){
return &pool[pi++];
}
typedef struct Graph{
int size;
Node *next;
Graph(){
size = 0;
next = 0;
}
void push_back(int nodeNumber){
Node *newNode = alloc();
newNode->number = nodeNumber;
newNode->next = next;
next = newNode;
size++;
}
};
bool check[MAX_NODE_SIZE+1];
Graph graph[MAX_NODE_SIZE + 1];
void dfs(int node){
if(check[node]) return;
check[node] = true;
cout << node << ' ';
Node *cur = graph[node].next;
for(int i = 0; i < graph[node].size; i++){
dfs(cur->number);
cur = cur->next;
}
}
int main(){
graph[1].push_back(2);
graph[1].push_back(4);
graph[1].push_back(5);
graph[2].push_back(1);
graph[2].push_back(3);
graph[2].push_back(6);
graph[3].push_back(2);
graph[4].push_back(1);
graph[4].push_back(6);
graph[5].push_back(1);
graph[6].push_back(2);
graph[6].push_back(4);
dfs(1);
}결과
1 5 4 6 2 3 사실상 이전에 했었던 쌩구현 Graph빼면, DFS부분은 stl이나 그냥 구현이나 별반 다를바가 없다.
이렇게 DFS가 끝났다. 사실 DFS는 그렇게 자주 문제풀 때 사용하진 않는다. 찔러 들어간다는 개념과 다시돌아간다는 개념이 주요하게 쓰일 때가 있긴하지만, 코딩 테스트나 많은 문제들은 DFS보다 BFS를 써야하는 경우들이 많다. 또한, 대부분의 DFS문제가 BFS로 해결되기 때문에 BFS를 주요하게 보아야 한다.
이유는 다음 시간에!!
