[크루스칼 알고리즘 (Kruskal Algorithm)] MST 찾기 알고리즘 (간선 중심)

선수과목

유니온-파인드 알고리즘

---

MST 란?

V개의 정점(Vertex), E개의 간선(Edge) 가 있는 그래프를 가정

최소 신장 트리 (MST, Minimum Spanning Tree)

신장트리 : 그래프에서 모든 정점을 연결하고 있는 트리

최소신장트리 : 간선의 가중치(거리)가 최소인 신장트리

간선의 개수가 V-1 인 특징이 있다.

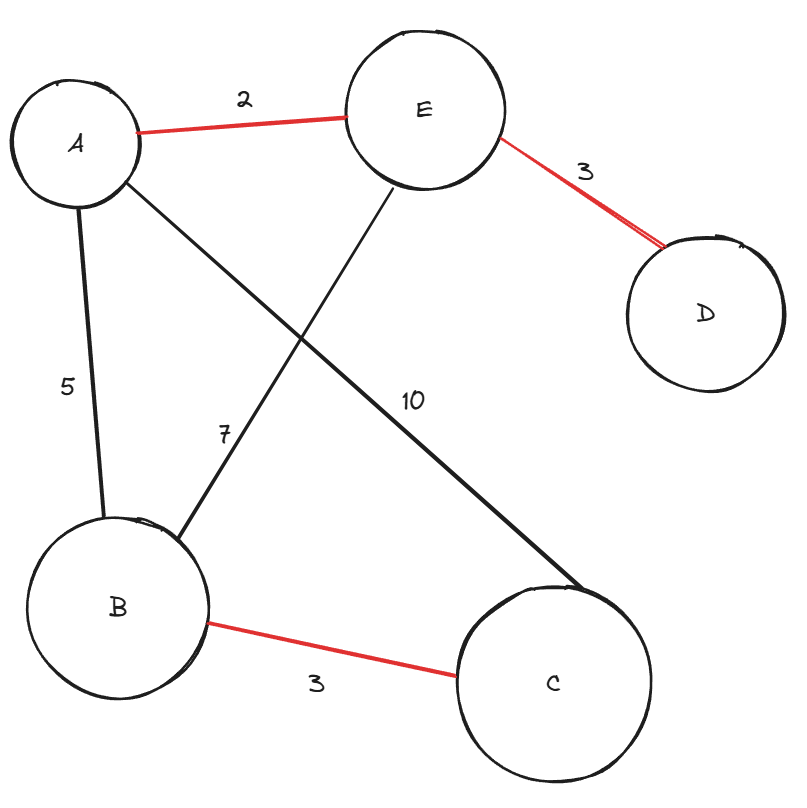
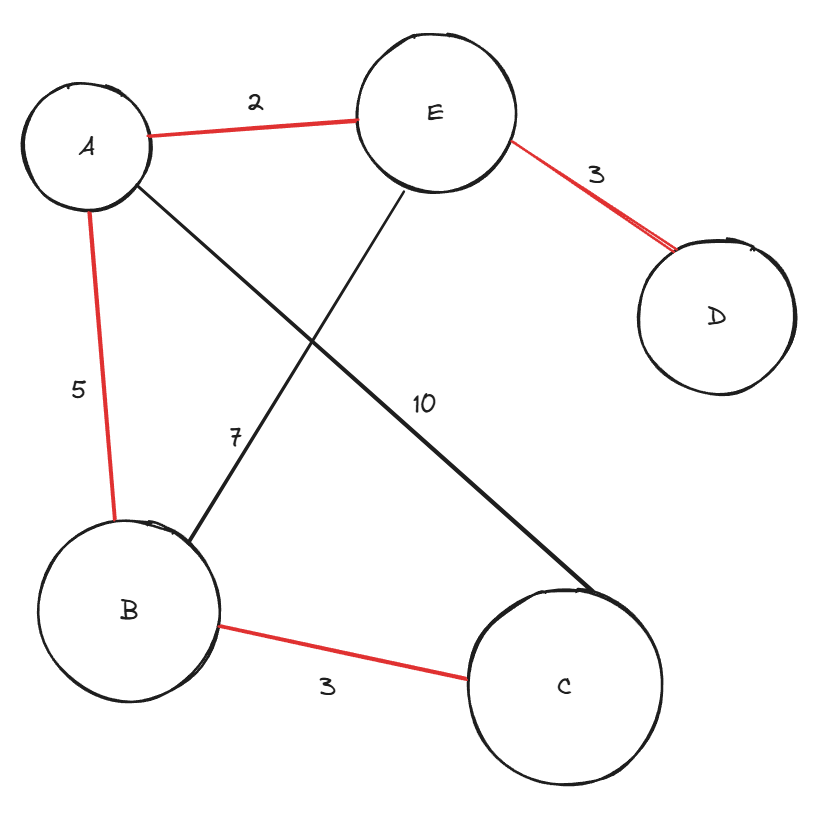
간선들 중에서 빨간색으로 선택된 간선들이 최소 가중치를 가지면서 모든 노드들을 연결한다.

MST 는 그리디 기법을 이용하여 최적의 해를 구할 수 있으며,
대표적으로 크루스칼 알고리즘과 프림 알고리즘이 있다.

오늘은 크루스칼 알고리즘에 대해 알아보자.

---

크루스칼 알고리즘 (Kruskal Algorithm)

MST 찾기 알고리즘 - 간선 리스트(Edge List) 중심

매 순간 최선의 선택을 하기에 그리디 알고리즘으로 분류된다

시간복잡도

경로 최적화 이용 X : $O(|E|log|V|)$
경로 최적화 이용 O : $O(|E|log^*|V|)$

---

왜 Union-Find 를 활용하는 알고리즘이냐?

알고리즘 과정

0. 전처리 : 간선 리스트를 오름차순 정렬
1. 모든 정점은 각각 크기가 1인 (자신이 root인) 트리. (make-set)
   => 간선을 아무것도 선택하지 않은 상황
2. 간선을 하나씩 선택 (두 정점을 연결) (union)
   • 두 정점(트리)이 같은 루트를 가지고 있으면 cycle 발생
3. 간선의 개수가 V-1 개가 될 때까지 반복

---

시뮬레이션

1. 가장 낮은 가중치의 간선 선택
   A - B (가중치 2)

   

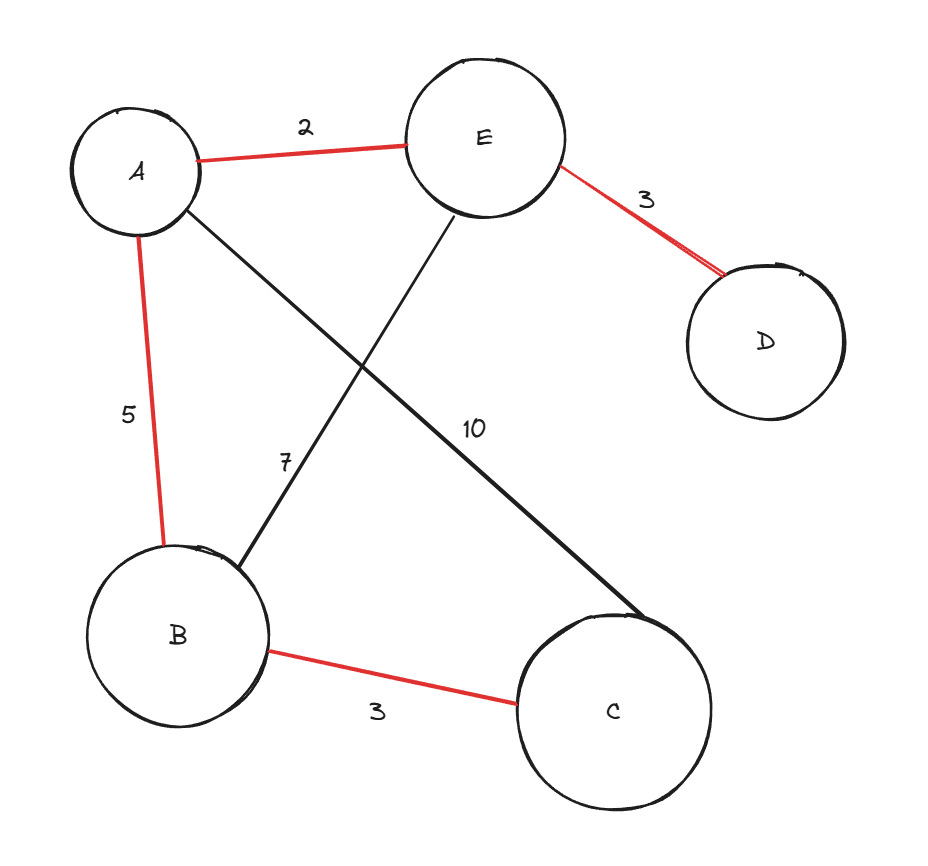
2. 그다음 낮은 가중치의 간선 선택
   가중치가 3인 간선이 2개 있으나, 아무거나 선택
   E - D (가중치 3)

   

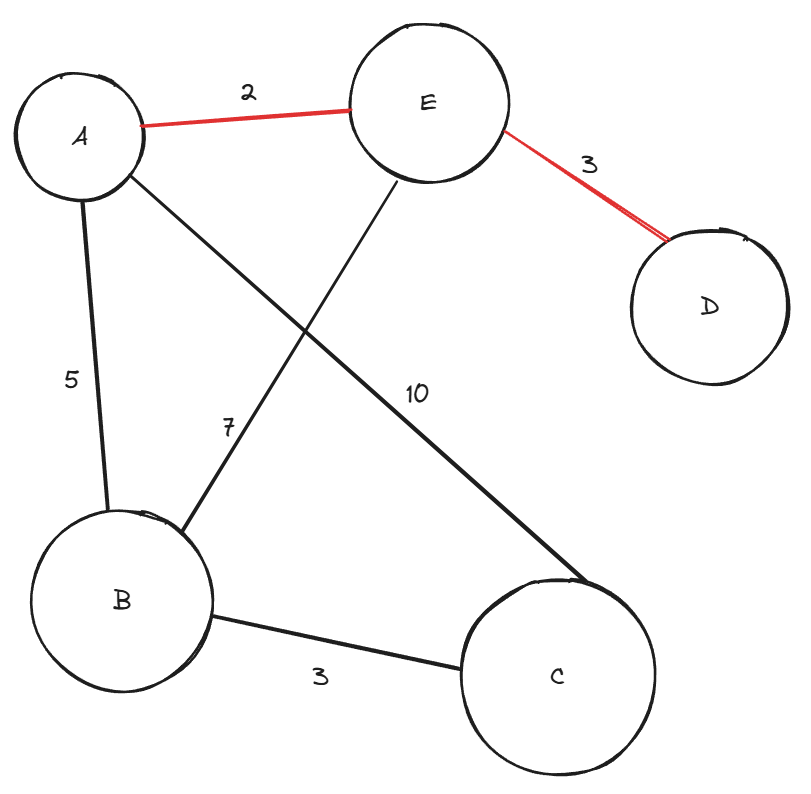
3. 그다음 낮은 가중치의 간선 선택
   방금 선택하지 않은 가중치 3인 간선 선택
   B - C (가중치 3)

   

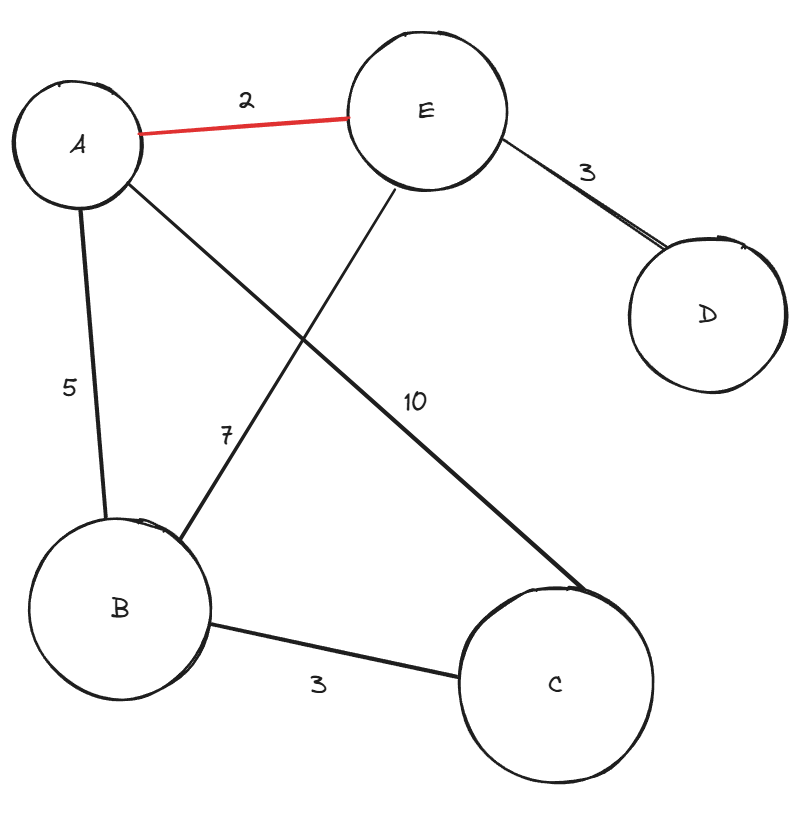
4. 그다음 낮은 가중치의 간선 선택

   ⚠️ 이 사진에서만 A - D (가중치 4) 간선을 넣어봤습니다. ⚠️
   이미 그림을 다 그렸었지만 싸이클이 발생하는 예시를 보여주고 싶었습니다

A - D (가중치 4) 가 그 다음으로 가중치가 낮은 간선이지만, 싸이클이 발생하기 때문에 선택하지 않고 넘어간다.

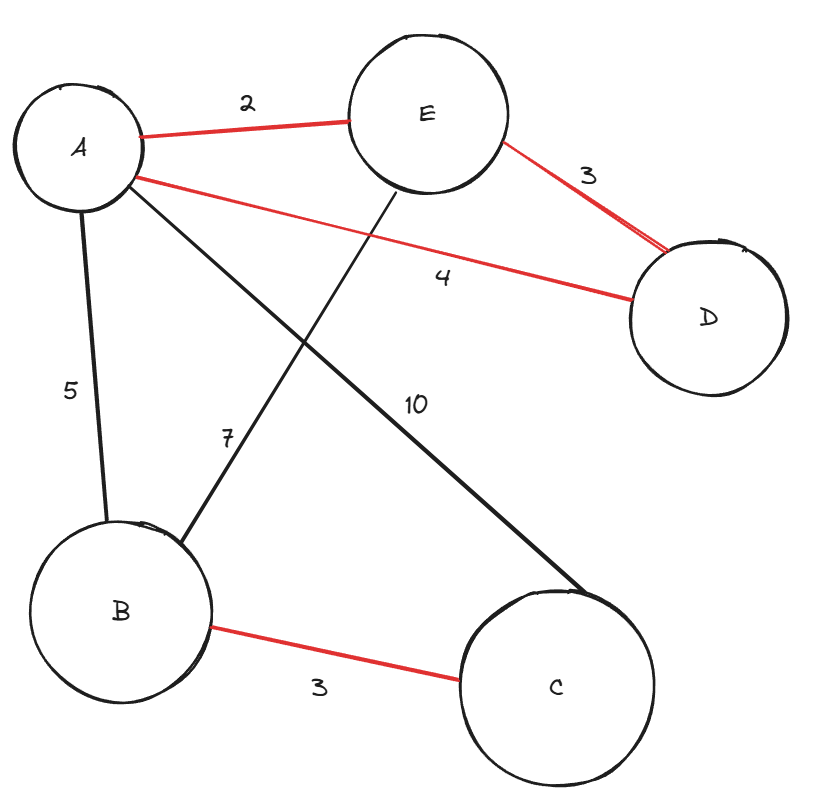
5. 그다음 낮은 가중치의 간선 선택
   A - B (가중치 5)

   

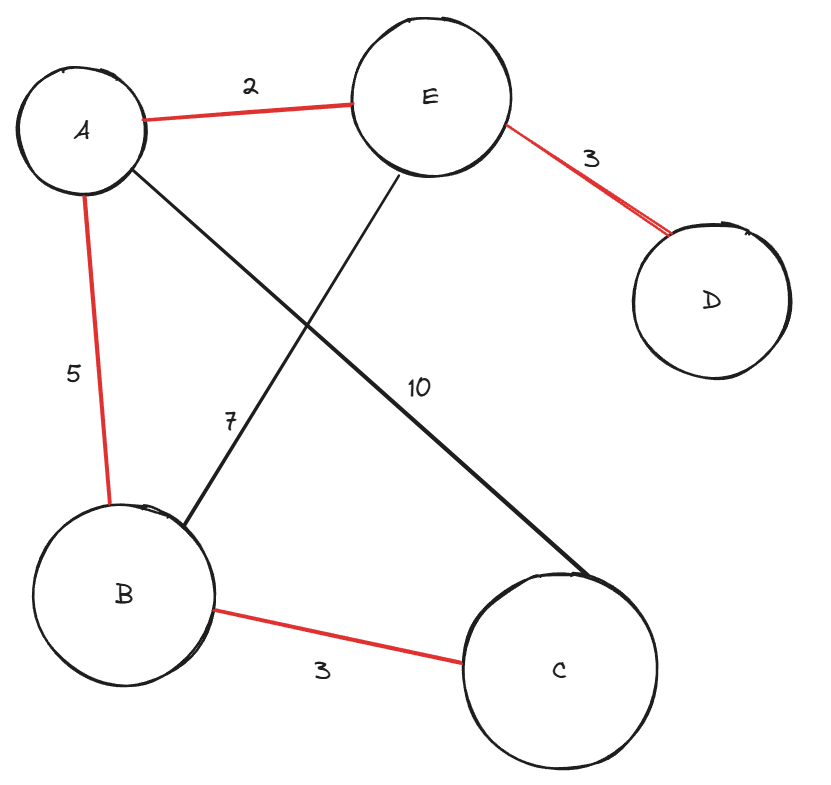
총 간선의 개수가 V-1 인 4개 이기 때문에 MST 완성 !
가중치는 총 2+3+3+5 = 13 이다

---

코드로 구현

Pseudo Code, 수도코드

// G.V : 그래프의 정점 집합, G.E : 그래프의 간선 집합
// n : 정점 수, cnt : 선택한 간선 수, weight : 선택한 간선들의 가중치 합
MST-KRUSKAL(G, w)
	cnt = 0, weight = 0;
    FOR vertex v in G.V
    	Make-Set(v)
	End For
    Sort(G.E) // G.E 에 포함된 간선들을 가중치 w를 이용한 오름차순 정렬
    FOR 간선 (u, v) ∈ G.E 선택 // 신장 트리의 구성으로 선택한 간선의 개수가 n-1개가 될 때까지 반복
    	IF Find-Set(u) != Find-Set(v) THEN
        	Union(u,v)
            cnt++		// 총 간선의 수 증가
            weight = weight + w		// 총 가중치 증가
            IF cnt == n-1 THEN		// MST 완성
            	break
			END IF
		END IF
	END FOR
END MST-KRUSKAL()

Java Code

public class MST_Test {
	static class Edge implements Comparable<Edge> {
    	int from, to, weight;
        
        public Edge(int from, int to, int weight) {
        	super();
            this.from = from;
            this.to = to;
            this.weight = weight;
        }
        @Override
        public int compareTo(Edge o) {
        	return Integer.compare(this.weight, o.weight);
		}
	}
    
    static int V;	// 정점 개수
    static Edge[] edgeList;
    static int[] parents;
    
    public static void main(String[] args) throws IOException {
    	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        V = Integer.parseInt(st.nextToken());		// 정점의 개수 입력
        int E = Integer.parseInt(st.nextToken());	// 간선의 개수 입력
        edgeList = new Edge[E];
        
        // from to weigth 로 간선 정보의 입력이 들어온다고 가정
        for (int i=0; i<E; i++) {
        	st = new StringTokenizer(br.readLine(), " ");
            int from = Integer.parseInt(st.nextToken());
            int to = Integer.parseInt(st.nextToken());
            int weight = Integer.parseInt(st.nextToken());
            
            edgeList[i] = new Edge(from, to, weight);
        } // 간선 리스트 생성
        
        // 전처리 : 간선 리스트 오름차순 정렬
        Arrays.sort(edgeList);
        
        // 1. make - set
        make();
        
        // 2. 정렬된 간선하나씩 꺼내어 신장트리 생성
        int weight = 0;
        int cnt = 0;
        for (Edge edge : edgeList) {
        	if (!union(edge.from, edge.to)) continue;
            weight += edge.weight;
            if (++cnt == V-1) break;		// 최소신장트리(MST) 완성
		}
        
        System.out.println(weight);
    	
	}
    
     public static void make() {
     	parents = new int[V+1]; 	// 자신의 부모나 루트(경로 압축) 저장
     	for (int i=1; i<=V; i++) {
        	parents[i] = i;		// 모든 정점을 자신을 루트로
        }
	}
    
    public static int find(int a) {		// a가 속한 트리의 루트 찾기
		if (a == parents[a]) return a;
        
        return parents[a] = find(parents[a]);		// 경로 압축
	}
    
    public static boolean union(int a, int b) {
    	int aRoot = find(a);
        int bRoot = find(b);
        if (aRoot == bRoot) return false;		// a,b 가 같은 트리에 속해있다 => union 불필요
        
        parents[bRoot] = aRoot;
        return true;
	}
}

---

관련 문제

백준 - 최소 스패닝 트리

MST의 가중치를 출력하는 문제.
위 java 예시 코드를 그대로 넣으면 정답이다.

---

더 많은 문제들 ↓

백준 최소 스패닝 트리 카테고리