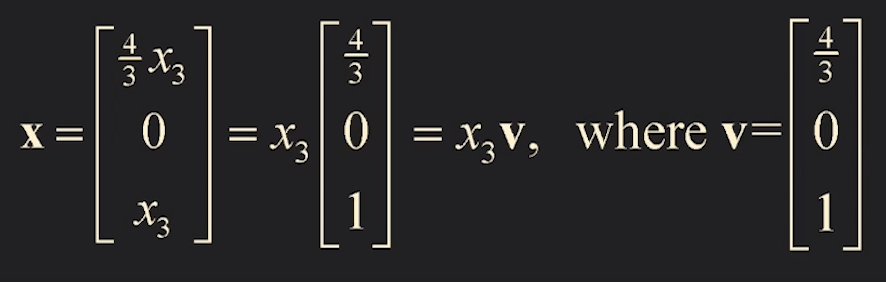1.5 Solution Sets of Linear Systems

조범희 선생님의 선형대수학개론 강의를 듣고 공부하며 정리한 내용입니다.
정말 좋은 강의힙니다. 강추합니다. 링크

 

Homogeneous Linear Systems

A x = 0

always has at least one solution x = 0

 
trivial solution - 너무 당연한 solution 이라서 그런지 trivial solution 이라고 함

 
nontrivial solution

if and only if the equation has at least one free variable (by Theorem2.)

 

Example1. Determine whether there is a nontrivial solution

$\begin{aligned} 3x_1 + 5x_2 -4x_3 = 0\\ -3x_1 -2x_2 +4x_3 = 0\\ 6x_1 + x_2 -8x_3 = 0 \end{aligned}$

 

이 문제를 풀어보면 $x_3$ 가 free variable 로 나타난다 (infinite number of solutions)

이러한 꼴이 되는데

이는 즉, Span { v } 이다 (vector v 에 $x_1$이라는 scalar 값이 scalar multiplication 된 것이므로)

그리고 다시, 이는 Line 임을 말해준다 ( $\mathbb{R}^3$ 에서 span { v } 는 line 이므로)

 

Example 2. Determine whether there is a nontrivial solution

 

$10x_1-3x_2-2x_3 = 0$

 

$\bold{x}= \begin{bmatrix} 0.3x_2 + 0.2x_3\\ x_2\\ x_3 \end{bmatrix} \begin{bmatrix} 0.3x_2\\ x_2\\ 0 \end{bmatrix} +\begin{bmatrix} 0.2x_3\\ 0\\ x_3 \end{bmatrix}= x_2\begin{bmatrix} 0.3\\1\\0 \end{bmatrix}+ x_3\begin{bmatrix} 0.2\\0\\1 \end{bmatrix}$

 

→ Span $\begin{Bmatrix} \bold{u}, \bold{v} \end{Bmatrix}$

→ plane!

 


따라서,

A x = 0

• the solution set can always be expressed as Span $\begin{Bmatrix}\bold{v_1}, \cdots, \bold{v_p}\end{Bmatrix}$

• trivial solution is Span $\begin{Bmatrix}0\end{Bmatrix}$

 

Nonhomogeneous Linear Systems

 

Example 3. Describe all solutions of A x = b

 
$A = \begin{bmatrix} 3 & 5 & -4\\ -3 & -2 & 4\\ 6 & 1 & -8 \end{bmatrix} \quad b = \begin{bmatrix} 7\\-1\\-4 \end{bmatrix}$

이때의 A는 Example 1.과 동일하다

Example 1.에서는 Span$\begin{Bmatrix} \bold{v} \end{Bmatrix} , \bold{v} = (\frac{4}{3}, 0. 1)$ 이었는데 이를 유념해서 이 문제의 결과를 지켜보자

 

Solution.

 

$\begin{bmatrix} 3 & 5 & -4 & 7\\ -3 & -2 & 4 & -1\\ 6 & 1 & -8 & -4 \end{bmatrix} \sim\begin{bmatrix} 1 & 0 & -\frac{4}{3} & -1\\ 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 0 \end{bmatrix}$

으로

$\bold{x} = \begin{bmatrix} -1 + \frac{4}{3}x_3\\ 2\\ x_3 \end{bmatrix} =\begin{bmatrix} -1\\ 2\\ 0 \end{bmatrix} +x_3\begin{bmatrix} \frac{4}{3}\\ 0\\ 1 \end{bmatrix}$ 이 된다

 

이는 $\bold{x} = \bold{p} + x_3\bold{v} = \bold{p} + t\bold{v}$ 가 된다.

(p = particular solution으로, $A\bold{x} = \bold{b}$의 solution 중 특정한 하나의 solution이고,

v = homogeneous solution 으로, $A\bold{x} = \bold{0}$ 의 모든 solution 이다.)

 

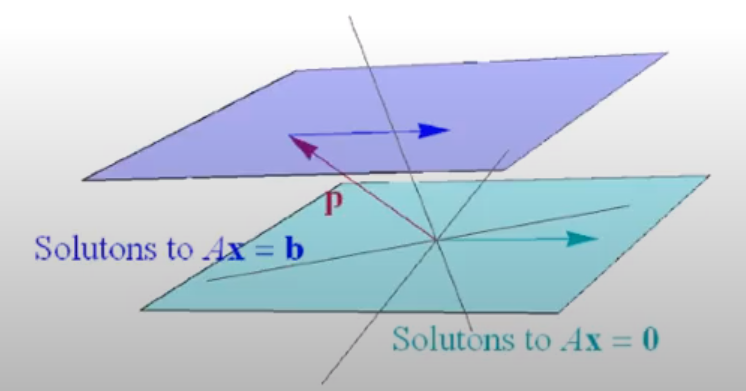
Theorem 6.

Suppose $A\bold{x} = \bold{b}$ is consistent (has a solution),

and let $\bold{p}$ be a solution ($A\bold{p} = \bold{b}$)

Then the solution set of $A\bold{x} = \bold{b}$ is the set of all vectors of the form

$\bold{w} = \bold{p} + \bold{v_h}$

where $\bold{v_h}$ is any solution of the homogeneous equation $A\bold{x} = \bold{0}$

 

Example 4. Understanding Theorem 6. in $\mathbb{R}^3$

(proof 와 visualization 은 링크 를 참고했다)

 

Theorem 6.를 증명하려면,

1) $\bold{p} + \bold{v_h}$ 꼴의 vector 가 $A\bold{x}=\bold{b}$ 의 해이면서

2) $A\bold{x}=\bold{b}$의 모든 해가 $\bold{p} + \bold{v_h}$의 꼴을 가지면 된다

 

이렇게 되면 '$\bold{p} + \bold{v_h}$ 꼴의 벡터'와 '$A\bold{x}=\bold{b}$의 모든 해' 라는 두 집합이 서로의 부분집합이 되면서, 두 집합은 동치이게 되고 이는 즉, Theorem 6과 같아진다

(다시 상기하자면, p = particular solution으로, $A\bold{x} = \bold{b}$의 solution 중 특정한 하나의 solution이고,

v = homogeneous solution 으로, $A\bold{x} = \bold{0}$ 의 모든 solution 이다.)

 

1)는 간단하다.

$A(\bold{p} + \bold{v_h}) = A\bold{p} + A\bold{v_h} = \bold{b} + \bold{0} = \bold{b}$

로 간단하게 해결이 된다.

 

(2)를 해결해보자

 

$A\bold{x}=\bold{b}$의 해인 $\bold{s}$ 가 있다고 가정하자.

그렇다면 $\bold{s}-\bold{p}$는

$A(\bold{s} - \bold{p}) = A\bold{s} - A\bold{p} = \bold{b} - \bold{b} = 0$ 으로 인해

$A\bold{x}=\bold{0}$ 의 해이다.

즉, $\bold{s} - \bold{p}= \bold{v_h}$ 이므로, $\bold{s} = \bold{p} + \bold{v_h}$ 꼴이 된다.

즉 (2)가 해결됐다

따라서, Theorem 6. 은 참이다.

 

조범희 선생님의 visualization보다 이 유튜브의 visualization이 조금 더 잘 이해됐는데,

$\bold{p}$가 particular solution 이므로 고정된 vector로 놓고, $\bold{v_h}$는 homogeneous system의 all solution이니 계속 변화하는 벡터로 생각할 수 있다.

 

이때 $\bold{v_h}$가 직선이라고 생각하면, $\bold{w}$는 $\bold{v_h}$와 평행한 직선으로 나타나게 되는 것을 알 수 있다.

 

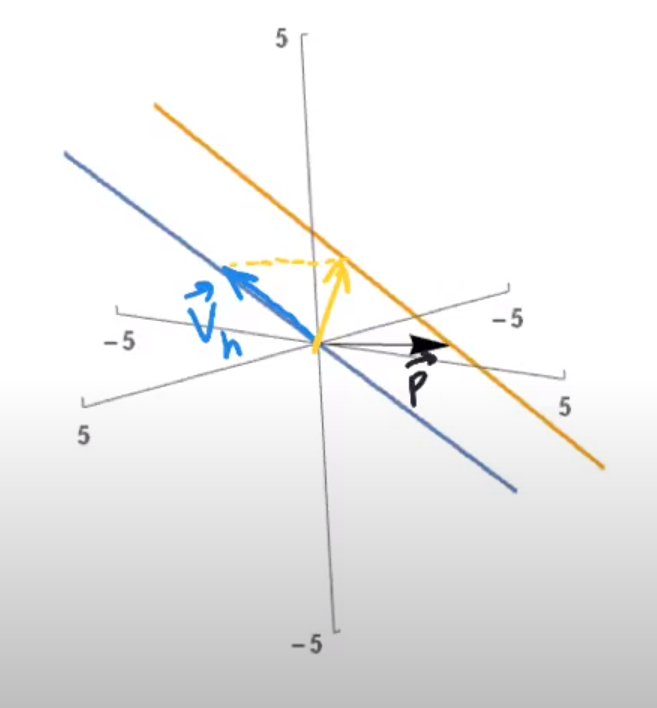
이를 일반화하면, 2차원에서 Theorem 6를 visualize 할 수 있다.