[썸네일 출처](사진: Unsplash의Ricardo Rocha
)

목차

• word2vec의 문제점
• Embedding 층
• 다중분류에서 이진분류로
• Embedding dot 층

---

1. word2vec의 문제점

simpleCBOW는 softmax층으로 단어의 출현 확률을 계산하였다. 하지만 말뭉치가 커지면 연산량이 많아지는데, softmax의 시간 복잡도도 O(N)으로, 단어 수가 100만 개가 넘어가면 상당히 학습하는 데 시간이 오래 걸린다는 문제가 있다.

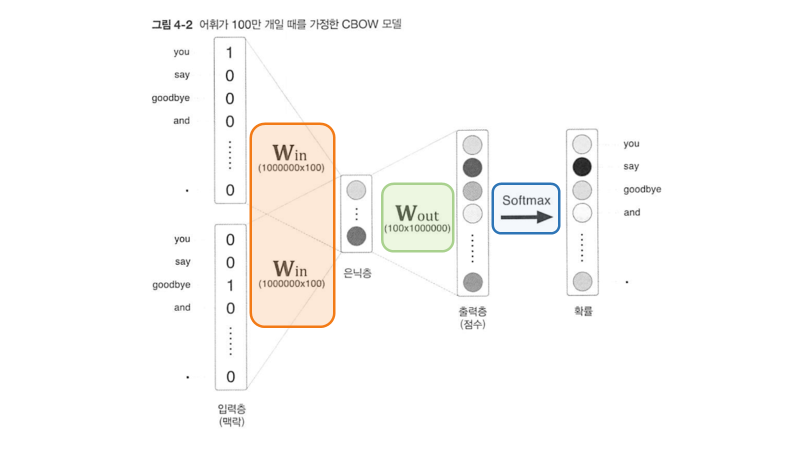
특히 입력값과 W_in의 행렬곱층, 은닉층과 W_out의 행렬곱층, Softmax계산 세 군데에서 병목 현상이 발생한다.

2. Embedding 층

직접적으로 softmax의 연산량을 최적화해주지는 못하나 학습 과정을 최대한 줄이는 것이 효율적이다. 단어가 많아질 수록 차이는 클 것이다.

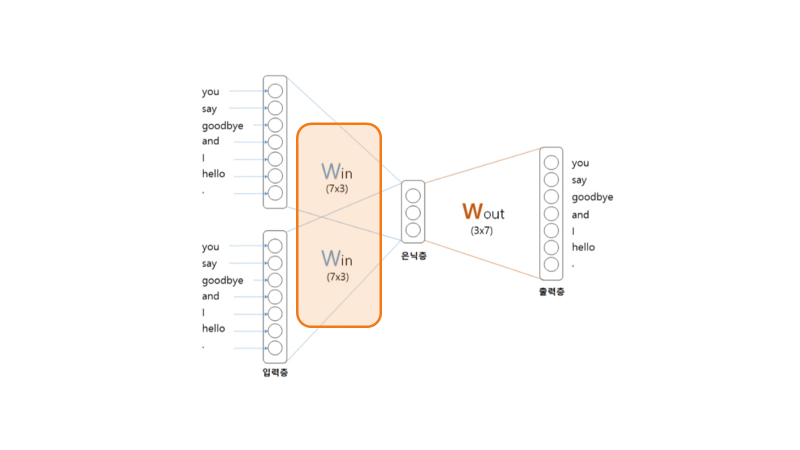
앞서 SimpleCBOW의 학습 과정에서 입력 데이터를 입력 가중치 행렬(W_in)과 합성곱하는 층에서 계산 작업을 줄일 수 있다. 입력 데이터가 원핫 행렬이기 때문에 입력 데이터와 W_in의 행렬곱은 W_in을 슬라이싱하는 것과 상동이다.

역전파도 패턴을 일반화하여 과정을 줄일 수 있는데 미분의 각 행을 해당 단어 인덱스 위치에 더하는 것이다.

class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None

    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

    def backward(self, dout):
        dW, = self.grads
        dW[...] = 0
        np.add.at(dW, self.idx, dout)
        return None

코드 출처

class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None

: Embedding층을 구현한 클래스이다. 초기화 메소드의 입력 파라미터는 W로 입력, 출력 구분 없이 Weight matrix이기만 하면 된다. 입력받은 W를 self.params에 저장하고, (리스트를 덧씌운 것은 Affine층 등과 형식을 맞춰주기 위함이지 큰 의미는 없다), self.grads는 기울기를 저장할 리스트로. W와 동일한 shape으로 초기화를 해준다. self.idx는 가중치 W로부터 추출하는 행의 인덱스(단어 ID) 배열이고, None으로 초기화해준다.

    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

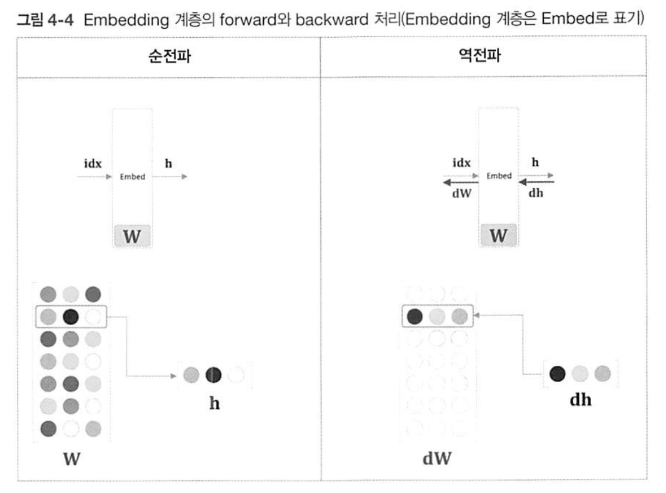
: forward()메소드는 idx를 입력 파라미터로 받고 있다. W, = self.params는 객체의 params 속성에서 가중치 텐서 W를 가져온다. 코드의 왼쪽에 있는 ,는 이터러블(unpackable)한 요소를 변수에 할당하기 위해 되는데 self.params가 하나의 요소만을 가지고 있는 튜플 형태라면 이렇게 요소를 추출할 수 있다. out = W[idx]는 가중치 텐서 W에서 인덱스 idx에 해당하는 값을 추출하여 out 변수에 할당한다.

    def backward(self, dout):
        dW, = self.grads
        dW[...] = 0
        np.add.at(dW, self.idx, dout)
        return None

: 가중치 기울기dW를 self.grads속성으로부터 꺼낸 다음, dW[...] = 0에서 dW의 원소를 형태는 유지한 채 내용만 모두 0으로 덮어씌운다. 그리고 앞 층에서 전해진 기울기 dout을 dW의 idx번째 행에 할당한다. 그림으로는 [그림 4-4]와 같이 된다.

def backward(self, dout):
    dW, = self.grads
    dW[...] = 0
    dW[self.idx] = dout
    return None

만일 위와 같이 backward()을 구현한다면 idx가 중복될 때 문제가 발생한다.

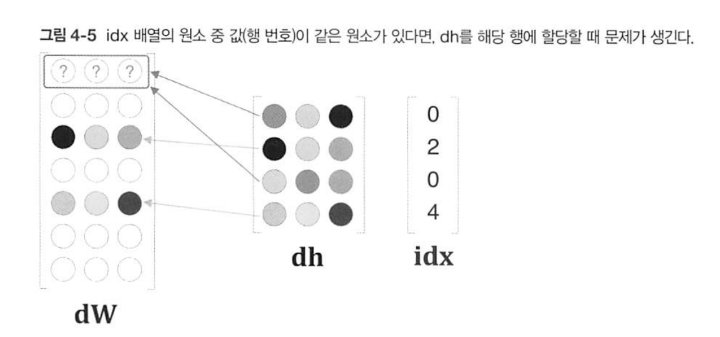
만일 [그림 4-5]와 같이 할당을 하면 중복되는 부분은 덮어쓰게 된다. 하지만 같은 인덱스라고 기껏 학습시킨 가중치를 덮어쓴다는 것은 중요한 정보를 버리는 것과 같다. '얼마만큼의 무게를 실어서 정답을 지지하느냐'의 척도와도 같은 가중치는 음수이건 양수이건 더하는 것이 합리적으로 보인다. 덮어쓰기에서 더하기로 바꾼 역전파를 구현한 코드이다.

def backward(self, dout):
    dW, = self.grads
    dW[...] = 0    
    for i, word_id in enumerate(self.idx):
        dW[word_id] += dout[i]
    # 혹은
    # np.add.at(dW, self.idx, dout)    
    return None

이렇듯 Embedding 층을 통해 입력값과 W_in의 행렬곱층에서의 병목현상을 해결할 수 있다. 이제 남은 문제는 은닉층과 W_out의 행렬곱층과 Softmax계산에서의 병목이다.

3. 다중분류에서 이진분류로

이진분류란 O,X문제와 같이 2가지의 선택지 중 하나를 답으로 선택하는 분류 문제이다. CBOW는 Skip-gram과 달리 embedding층 적용이 불가능한데, 그 이유는 아래 그림에서 확인할 수 있다.

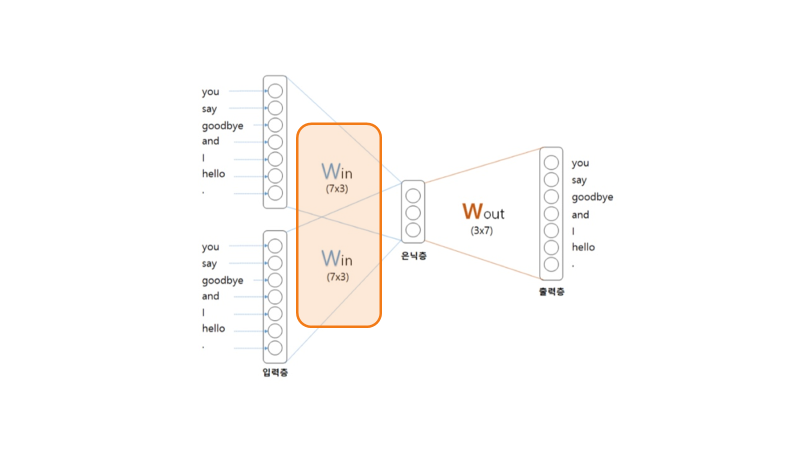
입력값이 2개일 때 은닉층은 두 벡터의 평균이기 때문에 원핫 벡터가 아니게 된다. 하지만 Skip-gram도 대규모 데이터에 대해 사용할 수 있는 방법이 있는데, 그 대안이 Embedding dot층이다.

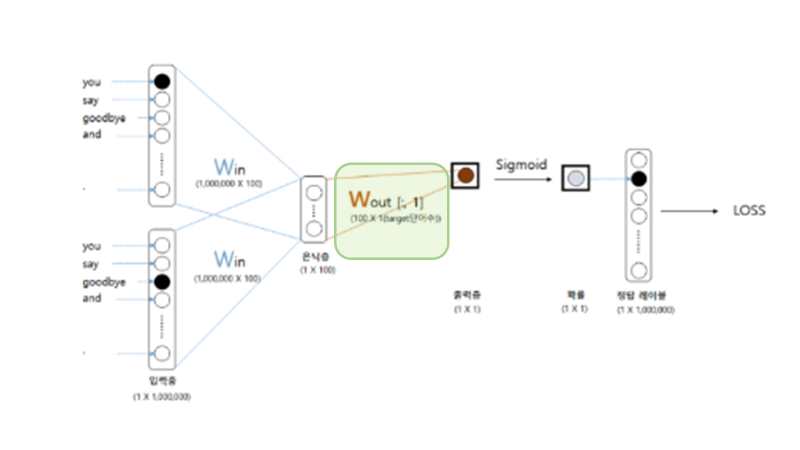
Embedding Dot층은 위 그림과 같이 출력 가중치 행렬(W_out)에 대해 적용할 수 있는 방안이다. 조건은 softmax대신 sigmoid를 사용해 출력값을 원핫 벡터 형식으로 만드는 것이다. 6지선다였던 다중분류 문제를 이진분류로 바꾸는 아이디어는 다음과 같다.

[기존] 다음 중 'you'와 'goodbye'의 사이에 올 단어는?
① you
② say
③ goodbye
④ and
⑤ i
⑥ hello
⑦ .

[수정]
'you'와 'goodbye'의 사이에 올 단어는 'say'이다. (O,X)

이렇게 되면 출력층에는 뉴런이 하나만 필요하게 된다. 출력층의 뉴런이 'say'의 점수를 출력하는 것이다.

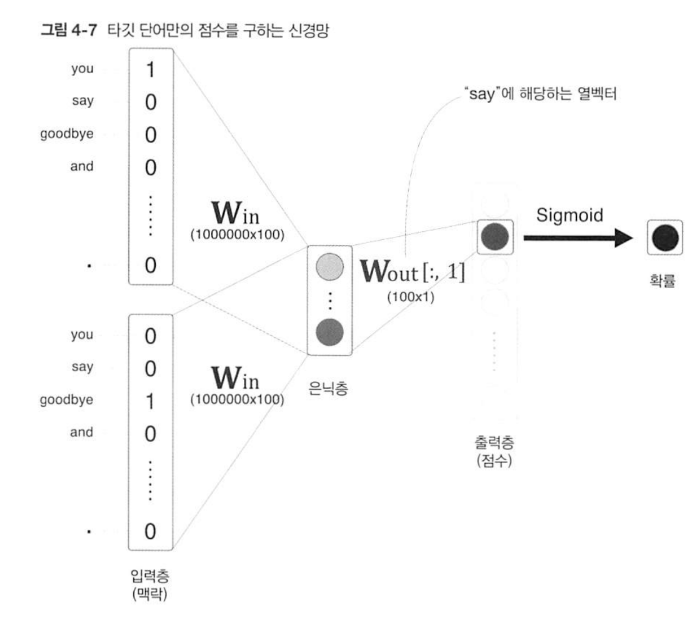
한 번에 두 가지의 문제를 해결해버렸다! [그림 4-7]에서 보듯 출력층의 뉴런은 하나뿐이다. 따라서 은닉층과 출력 측의 가중치 행렬의 내적은 'say'에 해당하는 열(단어 벡터)만을 추출하고, 그 추출된 벡터와 은닉층 뉴런과의 내적을 계산하면 끝이다. 즉, sigmoid의 시간 복잡도는 O(1)인 것이다.

4. Embedding dot 층

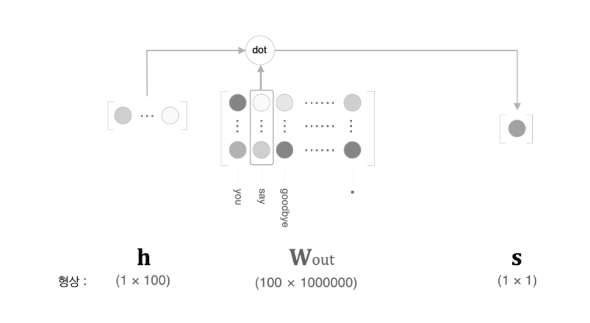
[그림 4-8]처럼 출력 측의 가중치(W_out)에서는 각 단어 ID의 단어 벡터가 각각의 열로 저장되어 있다. 이 예시에서는 'say'에 해당하는 단어 벡터를 추출한다. 그리고 그 벡터와 은닉층 뉴런과의 내적을 구한다. 이렇게 구한 값이 최종 점수가 된다.